교차 원통형 흐름: 압력 분포 측정 및 항력 계수 추정

비차원 압력 계수, C_p,임의의 각도 위치에서 이상적인 잠재적 흐름 이론의 임의 위치에 대한, θ, 원형 실린더의 표면에 다음 방정식에 의해 주어진다:

압력 계수 C_p는 다음과 같이 정의됩니다.

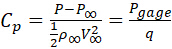
P가 절대 압력인 경우 _P∞는 방해받지 않는 자유 스트림 압력, P_게이지 = P - P ∞ 게이지 압력이며, 자유 스트림 밀도, _∞,및 공기 속도, V_∞기반의 동적 압력입니다.

이상적인 잠재적 흐름 이론에 의해 예측된 유동 패턴은 도 1에표시됩니다. 흐름은 대칭이므로 순 드래그 힘이 0입니다. 이를 D'Alembert의 역설 [1]이라고 합니다.

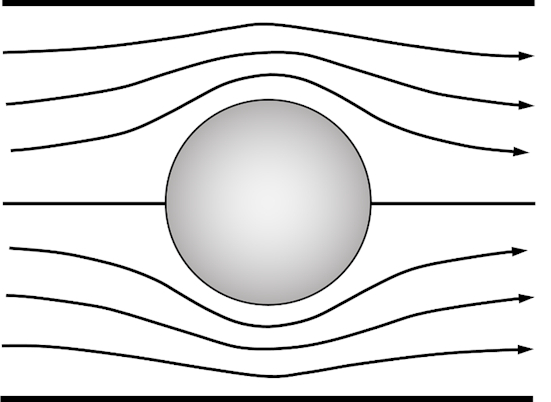
그림 1. 풍동에서 이상적인 교차 원통형 흐름의 흐름 패턴.

그러나 실제 흐름 조건에서는 순 제로 드래그 힘이 예상되지 않습니다. 압력 차이로 인해 실린더의 단위 길이당 인F_D의드래그 힘은 다음과 같은 것입니다.

통합은 실린더의 둘레를 따라 수행됩니다.

이 실험에서는 실린더를 따라 24개의 압력 포트에서 게이지 압력 측정이 수집됩니다. 그런 다음 위의 방정식은 측정된 게이지 압력을 사용하여 다음과 같이 수치적으로 평가될 수 있습니다.

여기서 P_{게이지i는} θ_i의위치에 게이지 압력이고, θ_i는 각 위치이고, r은 실린더의 반지름이며, 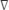θ는 15°인 인접한 포트 사이의 각도 거리이다. 게이지 압력은 24개의 독립적인 컬럼이 있는 기마계 패널을 사용하여 결정되며, 게이지 압력은 다음 방정식을 사용하여 결정됩니다.

여기서 Δh는 자유 스트림 압력을 참조하여 기마계의 높이 차이인 경우, _Lθ는 기마계내의 액체밀도이며, g는 중력으로 인한 가속이다. 드래그 포스를 얻으면 비차원 드래그 계수 C_D를 통해 결정할 수 있습니다.

여기서 d = 2r는 실린더의 직경입니다.

달렘베르트의 역설을 기억, 드래그 힘은 점도의 무시 효과 때문입니다. 첫째, 점성 힘의 결과로 원통을 따라 경계 층이 발생합니다. 이러한 점성 힘은 피부 마찰 드래그를 유발합니다. 둘째, 실린더는 절벽(간소화되지 않은) 오브젝트입니다. 이렇게 하면 유동 분리와 저압 절전 모드가 생성되고 압력 차이로 인해 더 큰 항력이 발생합니다. 도 2는 실험적으로 관찰되는 몇 가지 일반적인 흐름 패턴을 표시합니다. 실제 흐름 패턴은 다음과 같이 정의된 레이놀즈 번호 Re에 의존합니다.

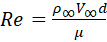
매개 변수μ 유체의 동적 점도입니다.

그림 2. 실린더를 통해 다양한 유형의 흐름 패턴.

깨끗하고 방해된 실린더에 대한 실험 결과는 각각 표 1과 2에표시됩니다. 데이터는 도 6에도시된 바와 같이 이상적이고 실제 흐름을 위해 압력 계수, C_p,각도 위치, θ 의 그래프로 플롯될 수 있다.

압력 포트 #	위치 각도 q(°)	기마계 판독값의 P게이지(물)	계산된 압력 계수 Cp
0	0	1.7	1.00
1	15	1.4	0.83
2	30	0.0	0.01
3	45	-1.7	-0.98
4	60	-2.7	-1.57
5	75	-3.7	-2.15
6	90	-3.3	-1.92
7	105	-3.0	-1.74
8	120	-3.2	-1.86
9	135	-3.2	-1.86
10	150	-3.3	-1.92
11	165	-3.5	-2.03
12	180	-3.4	-1.97

표 1. 클린 실린더에 대한 실험 결과. 대칭으로 인해 포트 번호 0-12에 대한 데이터만 표시됩니다.

압력 포트 #	위치 각도 q(°)	기마계 판독값의 P게이지(물)	계산된 압력 계수 Cp
0	0	1.8	1.05
1	15	1.6	0.93
2	30	0.6	0.35
3	45	-1.3	-0.73
4	60	-2.9	-1.69
5	75	-4.0	-2.31
6	90	-4.0	-2.33
7	105	-1.7	-0.99
8	120	-1.5	-0.89
9	135	-1.4	-0.84
10	150	-1.4	-0.84
11	165	-1.5	-0.87
12	180	-1.4	-0.84

표 2. 방해된 실린더에 대한 실험 결과. 대칭으로 인해 포트 번호 0-12에 대한 데이터만 표시됩니다.

그림 6. 압력 계수 분포, C_p,대 각 위치, θ, 이상적 및 실제 흐름 사이.

정체 점, θ = 0°에서 C_p는 C_p = 1의 최대 값에 도달합니다. 60°< θ의 경우 압력 계수 분포는 세 곡선 모두에 대해 유사합니다. 여기서 라미나르 경계 층 흐름이 실린더 표면에 부착됩니다. 60°> θ의 경우, 두 개의 실험적 흐름 패턴은 이상적인 흐름에서 벗어난다. 그들은 난류 소용돌이와 에디로 가득 실린더의 뒷면에 저압 영역을 형성한다. 이 영역이라고 합니다. 원통형 의 전방과 후면 사이의 압력 차가 교차 원통형 흐름에서 관찰되는 큰 드래그를 일으킨다.

깨끗한 실린더와 방해실린더 사이의 흐름 패턴의 유사성에도 불구하고 차이점도 있습니다. 방해된 흐름은 유동 분리 전에 실린더 를 감싸는 경향이 있으며, 또한 더 높은 역압을 가지고 있습니다. 이렇게 하면 드래그 계산에서 확인된 드래그가 줄어듭니다. 이는 실린더 앞의 라미나르 흐름이 직선으로 흐르는 경향이 있고 흐름이 실린더 주위를 감싸기 어렵기 때문에 발생합니다. 방해된 실린더의 경우 흐름은 즉시 난류 흐름으로 전환되므로 클린 실린더보다 실린더 를 감싸수 있습니다.

흐름 구성	드래그 계수, CD
1. 클린 실린더	1.68
2. 방해 실린더	0.78

표 4. 드래그 계수, C_D (레이놀즈 번호 Re = 1.78 x 10^5).

60mph 기속 또는 Re=178,000에서 클린 실린더용 드래그 계수 C_D는 실험적으로 평가되었으며 약 1.5 [2]이며, 이는 이 실험에서 얻은 1.68의 값에 가깝습니다.

이전 실험 결과 [2]에서 드래그 계수 C_D는 Re = 3 x 10^5에서떨어집니다. 이는 라미나르 흐름에서 격동의 흐름으로의 전환이 매끄러운 실린더에서도 자연스럽게 발생하기 때문입니다. 실험에서, 난류 흐름 전이는 단순히 실린더의 표면에 1mm 직경 문자열을 테이핑하여 관찰된다. 따라서, 0.78의 낮은 드래그 계수 _CD는 방해실린더에 대해 얻어진다.

교차 원통형 흐름은 18 세기부터 이론적으로 그리고 실험적으로 조사되었습니다. 둘 사이의 불일치를 찾아서 유체 역학에 대한 이해를 확장하고 새로운 방법론을 탐구할 수 있습니다. 경계 층 흐름 이론은 20 세기 초에 Prandtl [3]에 의해 개발되었으며, D'Alembert의 역설을 해결하기위한 비스타드 흐름 이론으로 비스티드 흐름의 확장의 좋은 예입니다.

본 실험에서, 교차 원통형 흐름은 풍동에서 조사되었고, 24개의 압력 측정 포트가 실린더의 표면을 따라 압력 분포를 찾아서 이루어졌다. 드래그 계수는 계산되었으며 다른 소스와 잘 동의합니다. 상대적으로 낮은 레이놀즈 수로 난류 경계 흐름을 트리거하는 흐름의 조작도 입증되었다.