Method Article
台湾におけるコホート効果を推定するための加重回帰モデルを用いた肝細胞癌死亡率の予測
要約
年齢データを使用してコホート効果を測定する多段階の方法を示し、データの品質を犠牲にすることなく、多くの状況でデータを排除することができます。このプロトコルは、戦略を実証し、肝細胞がんデータを分析するための加重回帰モデルを提供します。
要約
年齢サイクルの分割表データにおける年齢と期間の影響を排除するために、コホート効果を評価するために多段階の方法が採用されました。肝臓の最も一般的な原発性悪性腫瘍は肝細胞癌(HCC)です。HCCは、アルコールおよびウイルスの病因を伴う肝硬変に関連しています。疫学では、HCC死亡率の長期的傾向が、年齢-期間-コホート(APC)モデルを用いて描写(または予測)された。HCCによる死亡は、各コホートについて、その重み付けされた影響とともに決定された。加重平均の信頼区間(CI)は、(均等に加重された推定値と比較して)かなり狭くなっています。CIがかなり狭く、不確実性が少ないため、予測の手段として加重平均推定が使用されました。マルチステージ法では、回帰モデルに基づく加重平均推定を使用して、年齢-期間分割表データのコホート効果を評価することをお勧めします。
概要
肝臓の最も一般的な原発性悪性腫瘍は肝細胞がん(HCC)です。その死亡率は、世界中の悪性腫瘍の中で男性で5位、女性で8位(男性の6%、女性の3%) 1 にランクされています。台湾では、男性に多いがんであり、女性に2番目に多いがんです(男性の21.8%、女性の14.2%) 2。2000年以降、世界中で診断されたHCCの年間数は564,000人と推定されており、そのうち398,000人が男性、166,000人が女性です 3。疫学では、年齢、期間、およびコホート(APC)変数間の関係を説明する最も一般的な方法は、年齢と期間が互いに影響し合い、調査対象の疾患傾向に固有の世代体験を生み出すというものです。
この概念化には、年齢+コホート=期間の正確な線形関係がまだありますが、曝露(予測子)は出生コホートに固有の要因ではありません。代わりに、変化が疾患の分布を変える場合、コホート効果があることを提案する。それにもかかわらず、年齢 + コホート = 期間であるため、これら 3 つの変数は線形に関連しています。他の制限が施行されている場合にのみ、年齢、期間、およびコホートの線形効果を使用して推定年齢-期間-コホート(APC)モデルを生成することは不可能です。この研究では、この問題と、以前の出版物4,5,6,7で課した潜在的な制限を明らかにしました。
分割表のデータについてわずかな推測をすると、多段階法 8 はコホート効果を評価するための3つの段階を提供します。また、中央値のポリッシュは特定の分布やフレームワークに依存しないため、比率、対数比、カウントなど、さまざまな種類のデータに使用されました。中央値の研磨は、多相法で使用される主要な技術です。
二元配置分割表 9 からのデータを使用して、磨かれた中央値の発達を生成しました。中央値の研磨手順は、各行と各列から中央値を繰り返し減算することにより、年齢(つまり、行)と期間(つまり、列)の累積的な影響を排除するために使用されます。この手順は、疫学データ分析 10でよく使用されます。この手法の利点の 1 つは、双方向分割表のデータの分布や構造に関する仮定が不要であることです。したがって、この手法は、自殺データ 11など、テーブルに含まれる任意のタイプのデータに対して広く利用された。APCモデルは、疾患の発生率または死亡率の長期的な傾向を説明するためにも使用されてきました 5。APCモデルは、多くの場合、年齢、期間、およびコホートが疾患/死亡率の対数変換に相加的な影響を与えると仮定します。コホート効果を評価するために、記載されているプロトコルは、重み付け回帰による完全な肝細胞がん (HCC) 死亡率分析のための APC モデルを生成し、それにより、治療効果の信頼性の高い予測と中程度の評価をサポートします。
プロトコル
1. データソース
計算を実証するために、台湾の男性と女性の1976年から2015年までのHCC死亡率に関する年間データを使用しました。この研究のプロトコルを実行するために、WindowsおよびMicrosoft Excel用のStatistical Package for Social Sciences(SPSS)バージョン24.0が使用されました。
- HCC の医師に患者の臨床症状、臨床検査、および医用画像結果を分類してもらい、国際疾病分類 (ICD) コード、ICD 150 に従って診断コードを提供します。
- データファイル(CSVとして保存)に、年(期間)、年齢、コホート、死亡数、年半ばの人口数、および死亡率が列として含まれていることを確認してください。
- [ファイル] |データのインポート |CSVデータ |開いています。[データの最初の行から変数名を読み取る] の横にあるボックスにチェックが入っていることを確認し、[OK] をクリックします。データ・ファイルが SPSS にインポートされていることを確認します。
- SPSSを介して年齢-期間グループが交差する分割表データを作成します。一般に、行変数を年齢として定義し、列変数を期間として定義しました。データに単一期間の年(または単一の年齢の年)のデータが含まれている場合、それらを期間グループ(または年齢グループ)に統合する必要がありました。次に、調査年全体の年齢層に対する態度をクロス集計しました。
- [分析] |記述統計学 |クロス集計を行い、[行] の横のボックスで age 変数を選択し、[列] の横のボックスで [期間] 変数を選択します。[セル] をクリックし、[観察] の横のボックスにチェックが付いていることを確認します。死亡者数(または年央の人口数、または死亡率)の分割表は、上記の手順でSPSSで実行できます。
- CSV形式で入力された分割表のデータをエクスポートし、他のソフトウェアで分析することができます。 [ファイル] |データのエクスポート |必要なデータ形式をCSVとして確認する |場所。この編集不可のフィールドには、エクスポートされたファイルの安全な場所が表示されます。
- ファイル名: [選択 ] をクリックしてファイル名を変更します。
- エクスポートの種類: ドロップダウンメニューからCSVファイルの種類を選択します。 「変数 」をクリックして、使用可能な変数を表示し、変数テーブルを選択します。デフォルトでは、ソース・データ・セットのすべての変数は、エクスポートされたファイルに対して保持されます。研究者は、テーブルを使用して、エクスポートされたファイルに含めるソース変数を指定できます。 「エクスポート」をクリックします。
2. モデル設定
注:多段法は、KeysとLi 8 によってグラフィカルな調査とともに提案されました。年齢と期間の累積的な影響を排除するために、中央値のポリッシュ分析が行われました。最後に、線形回帰モデルのコホートカテゴリのポリッシュフェーズの中央値からのこれらの残差を回帰させ、分割表のデータを使用してコホート効果を評価しました。
- 最初のフェーズとしてのグラフィカル表現
- 年齢グループと期間グループの折れ線グラフを作成します。年齢グループまたは出生コホート全体で出生コホートを調べるには、折れ線グラフで年齢またはサイクル間で出生コホートを描画します。
- 分割表の死亡率データを含む CSV ファイルをインポートします。 [ファイル] |オープン | フォルダから CSV ファイルを参照して選択します。[ファイル名]ボックスの横にあるドロップダウンリストで [すべてのファイル ]を選択することを忘れないでください。
- [開く] をクリックして CSV ファイルを開きます。死亡率のコンティンジェンシーデータの行と列を強調表示し、[挿入] |チャート |折れ線グラフ。
- 第2フェーズとしてのポリッシュの中央値分析
- 各行と各列から中央値を繰り返し減算して、年齢と期間の累積効果を排除します。中央値の研磨フェーズの後、回帰手順の残差を保持して、コホート効果を評価します。
- 全体の中央値と残差テーブルを計算します。分割表の死亡率データを含むCSVファイルをインポートします(2.1.1.2を参照)。
- LNは、分割表の死亡率データの各セルに使用されました。[数式] |Mathematical & Trigonometry Function を選択し、LN.
- 番号: 各セルの場所ラベルを入力します。分割表の死亡率データの各セルがLNを取得したことを確認します。[ 数式] |その他の機能 |[統計 ] を選択し、[ MEDIAN] を選択します。
- 番号1:最初のセル位置ラベルを入力します。
- 番号2:最後のセル位置ラベルを入力します。結果の中央値が分割表の左上の余白に格納されていることを確認します。元の値(つまり、LN死亡率データ)と全体の中央値の差を取ることによって、残差テーブルが作成されることを確認します。
- 行の中央値(つまり、各年齢グループの中央値)を計算し、応答年齢グループの行の中央値が計算されたことを確認します。[ 数式] |その他の機能 |統計学 |[MEDIAN] を選択します。
- 番号1:生サンプルの最初のセル位置ラベルを入力します。
- 番号2:原材料の最後のセル位置ラベルを入力します。結果の行の中央値が分割表の左マージンに格納されていることを確認します。
- 行の中央値から減算した後、新しい残差テーブルを作成します。新しい残差値のセットが行の中央値から作成され、各セルがその行の各応答変数から行の中央値を減算する値を取ることを確認します。[=] をクリックし、各行の全体的なセル位置ラベルが左マージンの中央値のラベルを減算していることを確認します。
- 列の中央値(つまり、各期間グループの中央値)を計算し、応答期間グループの列の中央値が計算されるようにします。[ 数式] |その他の機能 |統計学 |[MEDIAN] を選択します。
- 番号 1: 列の最初のセル位置ラベルを入力します。番号 2: 列の最後のセル位置ラベルを入力します。結果の列の中央値が分割表の上マージンに格納されていることを確認します。
- 列の中央値から減算した後、新しい残差テーブルを作成します。新しい残差値のセットが列の中央値から作成され、各セルがその列の各応答変数から列の中央値の減算の値を取ることを確認します。[=] をクリックし、各列全体のセル位置ラベルが上余白の中央値のラベルを減算していることを確認します。
- 行と列の中央値がゼロに近づくまで、手順2.1.2.7から2.1.2.10を繰り返します。[ 数式] |その他の機能 |統計学 |[MEDIAN] を選択します。行と列の中央値がほぼゼロであることを確認してください。最終的な残差テーブルを CSV 形式で保存します。
- 重みを第 3 フェーズとする回帰手順
注:従属変数は、死亡者数を重みとして、各コホートの残差として計算しました。次に、線形回帰を実行してコホート効果を計算しました。- Kutools for Excelがインストールされていることを確認し、それを使用します 転置テーブル寸法 クロステーブルをフラットリストにすばやく変換するツール。分割表の残差データを含むCSVファイルをインポートします(2.1.2.11を参照)。
- リストに変換するテーブルを選択します。 Kutoolsをクリックします|変更 |転置テーブル次元。[転置テーブル寸法]ダイアログボックスで、[クロステーブル]リストの横にあるチェックボックスがオンになっていることを確認し、[結果範囲]を選択して残差をリスト形式で保存します。
- 初期データ・ファイル(1.2を参照)に、残差リスト形式のデータ(2.1.3.1を参照)を使用して列を挿入します。残差リスト形式のデータにサポート列が挿入されたことを確認します(2.1.3.1を参照)。「= age & period variables」をクリックし、「Enter」をクリックします。サポート列を使用して、残差リスト形式のデータの年齢および期間グループラベルを検索し、初期データファイルに応答残差列を挿入します(1.2を参照)。
- [ 数式] |ルックアップ&リファレンス |VLOOKUP を選択します。VLOOKUP を設定します (年齢のセル位置ラベルと期間のセル位置ラベル、支持列の最初のセル位置ラベル: 残差列の最後のセル位置ラベル、4, 0)。選択範囲に支持列、年齢列、期間列、残差列 (つまり、残差リストとして 4番目の 列) が含まれていることを確認します。
- 残差が初期データ・ファイル(1.2を参照)に挿入されていることを確認して、次のステップのために残差リスト形式のデータ(2.1.3.1を参照)を検索します。重み付けされていない最小二乗法で回帰モデルを当てはめ、残差を分析します。
- [分析] |回帰 |線形。独立変数のコホート・カテゴリー (つまり、17 の出生コホート) を「独立」ボックスに移し、従属変数の「残差」を「従属」ボックスに移します。[OK] をクリックします。重み付けされていないコホート効果の結果を生成することを確認します。
- 残差が最初の Excel データ・ファイル (1.2 を参照) に挿入されていることを確認して、次のステップのために残差リスト形式のデータ (2.1.3.1 を参照) を検索します。重み付き最小二乗法で回帰モデルを適合し、残差を分析します。 [分析] |回帰 |線形。
- 独立変数とコホート・カテゴリー (つまり、17 の出生コホート) を独立ボックスに、従属変数と残差を従属変数ボックスに移します。死亡番号をWLSウェイトボックスに移します。 [OK] をクリックします。コホート効果の加重平均の結果が生成されていることを確認します。
結果
死亡率データは、10の5歳年齢グループ(40-44、45-49、50-54、55-59、60-64、65-69、70-74、75-79、80-84、および85+)および8つの5年間(1976-1980、1981-1985、1986-1990、1991-1995、1996-2000、2001-2005、2006-2010、および2011-2015)で実証されました。コホートグループの数は、年齢グループの総数から1を引くことによって選択されました:10(5歳の年齢グループ)+8(5年間の期間)-1 = 17の出生コホート、出生コホートグループは、1891年、1896年、1901年、1906年、1911年、1916年、1921年、1926年、1931年、1936年、1941年、1946年、1951年、1961年、1966年、1971年として示されます。HCCの男性と女性の年齢層の偶発性の形式を提供します( 補足表1)。 図1 および 図2 は、年齢および期間グループ内のHCC死亡率を示しています。これらの変動は、女性よりも男性の間でより大きかった。年齢分布に基づく比率は、40〜44歳の年齢層の下限で、HCC死亡率が増加していることを示しています(図1)。対照的に、 図2 は、HCCの死亡率が≥60歳の年齢層で徐々に増加したことを明確に示しています。しかし、年齢に基づくHCC死亡率は時間とともに大幅に変化しており、これは、通常の年齢-期間の交差分類された人口動態統計表に隠された顕著なコホート効果が明らかになるのは、将来のある時点まで明らかになるということである。
私たちは、対数形質転換HCC死亡率の中央値研磨手順を実施しました。男性と女性のHCC死亡率のAPCモデルの推定コホート効果をそれぞれ表1と表2に示します。さらに、加重推定値を取得する前の2つの性別加重平均手順の計算は、 表1および表2に報告されています。重み付けされた推定値は、重み付けされた推定値の信頼区間(CI)の最小偏差(等しく重み付けされた推定値の比較)に基づいて、以前に推定されたコホート効果よりもデータによく適合します。
男性の場合、 表1 の左パネルは、出生コホートのコホート効果を示しています。コホート効果は、0.73(1891年の最も初期のコホート効果)から1.20(1936年の最大のコホート効果)に増加します。女性の場合、コホート効果は0.68(1891年の最も初期のコホート効果)から1.35(1936年の最大のコホート効果)に増加する。1891年のコホートと比較して、男性と女性のコホート効果がそれぞれ約64%と98%増加したことを強調することが重要です。増加は 、表2の右側のパネルに均等に分布しています。ここでは、コホート効果は0.71(1891年の最も初期のコホート効果)から1.11(1936年の最大のコホート効果)に増加しました。女性の場合、分布の増加による同様の効果が表2の右列で示されています。コホート効果は、0.64(1891年の最も初期のコホート効果)から1.11(1926年の最大のコホート効果)に増加した。したがって、男性と女性の最も初期のコホートと比較して、死亡率がそれぞれ約57%と73%増加したことが観察されました。
出生コホートの中で、1936年頃に生まれた男性はHCCによる死亡リスクが最も高いことを示しました(補足表1)。したがって、加重推定値では、1921年の参照出生コホートの影響と比較した1936年の出生コホートの影響は1.11(95%CI:1.08-1.14)であった。対照的に、1891年の以前のコホートは急激に増加傾向を示しました。さらに、1936年のコホート以降、影響は逆転しました。表1では、1916年の参照出生コホートと比較すると、加重効果は1.11(95%CI:1.07-1.16)であった。さらに、男性と女性について、それぞれ95%信頼区間を使用して、均等に重み付けされたコホート効果と重み付けされたコホート効果をモデル化しました。どちらの図も、同等に重み付けされたコホート効果が、95%CIのほぼすべての幅よりも広いことを示しています。
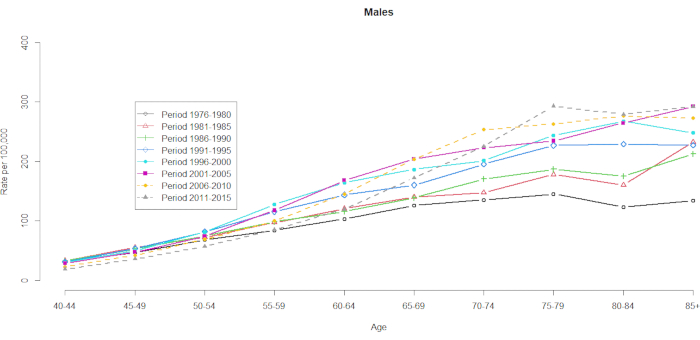
図 1.年齢および期間別の100,000人あたりのHCC死亡率、男性、台湾、1976-2015年。 この図の拡大版を表示するには、ここをクリックしてください。
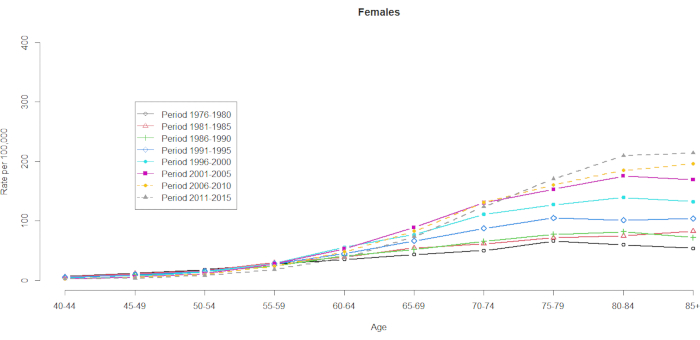
図 2.年齢および期間別の100,000人あたりのHCC死亡率、女性、台湾、1976-2015年。 この図の拡大版を表示するには、ここをクリックしてください。
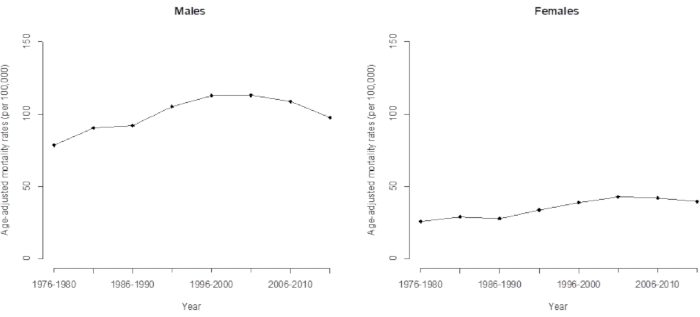
図 3.台湾の男性と女性の肝細胞がんによる年齢調整死亡率。 この図の拡大版を表示するには、ここをクリックしてください。
| 重み付けなし | 加重 | |||
| エフェクツ | エフェクトの95%CI | エフェクツ | エフェクトの95%CI | |
| コホート | ||||
| (1891~1971年) | ||||
| 1891 | 0.73 | 0.59-0.90 | 0.71 | 0.57- 0.88 |
| 1896 | 0.88 | 0.79-0.99 | 0.87 | 0.78- 0.97 |
| 1901 | 0.89 | 0.83-0.96 | 0.81 | 0.71- 0.92 |
| 1906 | 0.91 | 0.86- 0.97 | 0.85 | 0.78- 0.94 |
| 1911 | 0.95 | 0.90-1.00 | 0.89 | 0.83- 0.96 |
| 1916 | 1.01 | 0.97-1.06 | 0.99 | 0.95- 1.03 |
| 1921 | 1 | リファレンス | 1 | リファレンス |
| 1926 | 1.04 | 1.00-1.08 | 1.03 | 1.01- 1.06 |
| 1931 | 1.1 | 1.06-1.14 | 1.08 | 1.06- 1.11 |
| 1936 | 1.2 | 1.15- 1.24 | 1.11 | 1.08- 1.14 |
| 1941 | 1.14 | 1.09- 1.19 | 1.1 | 1.07- 1.13 |
| 1946 | 1.04 | 1.00-1.09 | 1.06 | 1.04- 1.09 |
| 1951 | 0.91 | 0.87-0.96 | 1 | 0.98- 1.03 |
| 1956 | 0.87 | 0.82-0.92 | 0.96 | 0.93- 0.98 |
| 1961 | 0.82 | 0.76-0.88 | 0.88 | 0.85- 0.92 |
| 1966 | 0.76 | 0.68- 0.85 | 0.79 | 0.74- 0.83 |
| 1971 | 0.71 | 0.57-0.87 | 0.83 | 0.80- 0.87 |
| 注:REF =参照。CI = 信頼区間。 | ||||
テーブル 1.1891年から1971年までの台湾の男性の肝細胞癌死亡率に対する出生コホートの影響に関する推定率比と95%会議間隔。
| 重み付けなし | 加重 | |||
| エフェクツ | エフェクトの95%CI | エフェクツ | エフェクトの95%CI | |
| コホート | ||||
| (1891~1971年) | ||||
| 1891 | 0.68 | 0.42- 1.10 | 0.64 | 0.38-1.09 |
| 1896 | 0.81 | 0.63-1.04 | 0.75 | 0.56- 1.00 |
| 1901 | 0.8 | 0.67- 0.95 | 0.7 | 0.52- 0.94 |
| 1906 | 0.83 | 0.72- 0.95 | 0.76 | 0.65- 0.88 |
| 1911 | 0.88 | 0.78- 0.99 | 0.85 | 0.78- 0.93 |
| 1916 | 1 | リファレンス | 1 | リファレンス |
| 1921 | 1.12 | 1.01-1.24 | 1.08 | 1.03- 1.13 |
| 1926 | 1.29 | 1.17-1.42 | 1.11 | 1.07- 1.12 |
| 1931 | 1.3 | 1.18-1.43 | 1.1 | 1.05- 1.15 |
| 1936 | 1.35 | 1.22-1.49 | 1.1 | 1.04- 1.14 |
| 1941 | 1.19 | 1.07-1.32 | 1.09 | 1.03-1.13 |
| 1946 | 1.05 | 0.94-1.17 | 1.06 | 1.02-1.11 |
| 1951 | 0.83 | 0.73-0.94 | 1 | 0.96-1.05 |
| 1956 | 0.67 | 0.58-0.77 | 0.93 | 0.89-0.98 |
| 1961 | 0.58 | 0.49-0.70 | 0.79 | 0.74-0.84 |
| 1966 | 0.59 | 0.46-0.75 | 0.58 | 0.49-0.69 |
| 1971 | 0.63 | 0.40-1.02 | 0.64 | 0.58-0.72 |
| 注:REF =参照。CI = 信頼区間。 | ||||
テーブル2.1891年から1971年までの台湾の女性の肝細胞癌死亡率に対する出生コホートの影響に関する推定率比と95%会議間隔。
ディスカッション
HCC死亡率の時間的傾向により、従来のモデルはデータに隠されたいくつかの重要な特徴(コホート効果など)を過小評価し、観察された対数年齢補正率の単純な線形外挿を使用する従来の分析では、予測の精度が大幅に低下しています。この傾向は35年間続いており、1976年から2015年までの台湾におけるHCC死亡率の長期傾向を直接観察すると、今後数年間で上昇傾向にあることは明らかです(図3)。実際、台湾におけるHCC死亡率の最近の傾向は減少しており、先に述べたように、1936年のコホート以降に減少したコホート効果(APC分析によって決定される)によって推進されている。この研究は、APCモデルの適用により、トレンドの変化に関する高度でより正確な警告が得られることを示しています。
臨床的な観点からは、B型肝炎ウイルス(HBV) 12に感染している人は約20億人おり、その結果、約3億5,000万人が罹患しています。その結果、これは世界的に高い罹患率を伴う重大な健康問題です。HBV感染は、肝炎、肝硬変、または肝細胞癌を発症させる効果のない保因者状態など、さまざまな臨床的問題を引き起こします。最も効果的な予防方法は、B型肝炎ワクチンを個人に接種することです。台湾は1984年に最初の世界的なB型肝炎集団予防接種計画を実施しました 13。このプログラムでは、妊婦はB型肝炎表面抗原(HBsAg)とB型肝炎エンベロープ抗原(HBeAg) 14のスクリーニングを受けました。このプログラムの最初の2年間は、予防接種プログラムはHBsAgの母親の赤ちゃんのみを対象としていました。しかし、ワクチン接種プログラムの3年目からは、すべての赤ちゃんが対象となりました。B型肝炎ワクチンの接種率は近年99%に達しています 15。約90%から95%の人が、ワクチンを3回接種した後、生涯にわたる免疫を経験するでしょう。台湾における小児HCCの減少は、主にこの世界的なワクチン接種プログラムに起因していることを強調します。
この記事で示す APC モデリングは、これらの (増加した) トレンドの変化 (近い将来に減少する) に関する高度な警告を提供します。コホート効果(表1および表2)と年齢調整死亡率(図3)の傾向を比較すると、直接年齢調整死亡率(または年齢標準化死亡率)は加重平均と同じであった。この研究では、2000年の世界標準人口 16 に基づいて、関心のある年齢層の割合によって年齢死亡率を重み付けします。コホート効果の検証がHCC死亡率の最新パターンの大部分を占めていたため、最新のデータ(2011-2015年まで)の年齢調整HCC死亡率を計算しました。これは、コホートの加重平均推定値が信頼できる情報を提供する一方で、将来のHCC死亡率を予測するための研究が準備されていることを意味すると解釈しました。HCCによる死亡率の予測に関する詳細は、 以前の研究5で確認できる。
一般的な仮説は、データ内の各値がモデル内のパラメーターを評価するための等しい情報を提供するというものです。このアプローチは、ほとんどのモデリング手法 (線形回帰モデルや非線形回帰モデルなど) で使用されており、誤差項の標準偏差が定数の基になる予測変数であることを意味します。しかし、私たちの文献レビューによると、この仮説はパラメータを経験的に推定するためのモデリングには適していません。未知のパラメータは、データポイントの精度が低い小さな重みとデータポイントの精度が高い大きな重みを生成する加重回帰を使用すると推定されます。重み付けプロセスにより、推定量の標準偏差が減少しました。それにもかかわらず、加重回帰法の欠点は、経験的実践ではほとんど知られていません。正確な重みは不明であるため、推定された重みを使用してパラメータを推定しました。さらに、これまでの経験から、推定に基づく重み付けは、回帰分析やその解釈17に有意に変化しないか、通常は影響しないことが実証されている。仮説的には、APCモデルは、発生率が年齢、期間、およびコホートによって影響を受ける任意の疾患に適合させることができます。さらに、予測18,19,20では、加重平均推定値が利用可能になりました。CIが比較的狭い場合、不確実性は小さくなります。CIがこの種の評価に内在する不確実性とその中の値を示しているという事実を考慮すると、CIを使用することは一般的に大きな影響を与えると結論付けます。
経カテーテル的動脈化学塞栓術 (TACE) は、HCC を臨床的に制御するための最も効率的な方法の 1 つです。しかし、この方法は開腹手術を必要としないため、一次治療または補助療法として選択することは困難です。肝臓は通常、肝臓の門脈を通じて血液と栄養素の75%を供給し、肝動脈は血液と栄養素の25%を提供します。ほとんどのHCCから抽出された肝動脈血とは対照的に、この体液は急速に増加し、肝門脈から来ることはめったにありません。さらに、原発性肝がんが体の他の部分に転移することはめったにないため、この効果はTACEによく適しています。肝細胞悪性腫瘍は転移する可能性は低いですが、根絶することは困難です。臨床診療では、HCC患者のフォローアップは2〜3か月ごとに行われます。α-フェトプロテイン(AFP)の異常な上昇または異常な超音波検査が検出されると、コンピューター断層撮影と磁気共鳴画像法が実行されます。新しい腫瘍が発見された場合は、TACEが考慮されます。HBV DNA定量的時間指数(HDQTI) 21など、HBV関連HCCの再発を検出するための新しいバイオマーカーも開発されています。フォローアップ結果と、検出されたHBV DNA負荷比と正常HBV DNA負荷比の対数の積がHDQTIの合計です。HDQTIは、HBV関連のHCC再発の独立した予後指標として使用されます 21。
私たちの研究にはいくつかの制限があります。まず、観察された変化の病因について仮説を立てただけです。APCモデルを用いて、年齢、期間、およびコホート効果によるHCC死亡率を再検討した。それにもかかわらず、本研究では、中央値の研磨設定を仮定として用いた。第二に、APC分析は、発展途上国または最近発展した国の疫学の分野で、長期コホート研究に広く使用されています。第三に、併存疾患やライフスタイルなどのAPCモデルの交絡因子を調整するための蓄積された形式のデータセットからの情報がありませんでした。この制限を解決するための将来の研究には、分離されたデータが必要です。第四に、多段階法の回帰手順を変更するために、HCCによる死亡者数を重みとして使用しました。正確な重量は不明であるため、さまざまな重量を使用すると、推定されたコホート効果内でわずかなインフレが発生します。最終的に、認識できない問題を解決するためのさまざまなAPC推定方法があります(たとえば、Holfordは認識できない問題を解くために線形トレンドと曲率トレンドを使用します 22)。同時に、中央値の洗練は、APCモデル間の概念変換の形で複雑な仮定を提供し、最も少ない仮定でコホート効果を評価し、分割表に共通の形式を容易に適用できます。
全体として、各コホートのCIが比較的狭い加重平均効果は、その後、回帰モデルを変更するための加重推定によって許容されました。簡単に言うと、多段階法では、回帰モデルの加重推定値を使用して、年齢-期間分割表データのコホート効果を評価することをお勧めします。
開示事項
著者は何も開示していません。
謝辞
本研究は、台北子智病院TCRD-TPE-109-RT-8(2/3)およびTCRD-TPE-109-39(2/2)の支援を受けました。
資料
| Name | Company | Catalog Number | Comments |
| not applicable | not applicable | not applicable | not applicable |
参考文献
- Kuntz, E., Kuntz, H. D. Hepatology: Principles and Practice. , Springer. New York. 774(2006).
- McGlynn, K. A., et al. International trends and patterns of primary liver cancer. International Journal of Cancer. 94 (2), 290-296 (2001).
- Bosch, F. X., Ribes, J., Diaz, M., Cleries, R. Primary liver cancer: worldwide incidence and trends. Gastroenterology. 127, 5-16 (2004).
- Tzeng, I. S., Ng, C. Y., Chen, J. Y., Chen, L. S., Wu, C. C. Using weighted regression model for estimating cohort effect in age-period contingency table data. Oncotarget. 9 (28), 19826-19835 (2018).
- Tzeng, I. S., Lee, W. C. Forecasting hepatocellular carcinoma mortality in Taiwan using an age-period-cohort model. Asia-Pacific Journal of PublicHealth. 27, 65-73 (2015).
- Tzeng, I. S., et al. Predicting emergency departments visit rates from septicemia in Taiwan using an age-period-cohort model, 1998 to 2012. Medicine. 95, 5598(2016).
- Chen, S. H., et al. Period and Cohort Analysis of Rates of Emergency Department Visits Due to Pneumonia in Taiwan, 1998-2012. Risk Management and Healthcare Policy. 13, 1459-1466 (2020).
- Keyes, K. M., Li, G. A multiphase method for estimating cohort effects in age-period contingency table data. Annals of Epidemiology. 20, 779-785 (2010).
- Tukey, J. Exploratory data analysis Reading: MS. , Addison-Wesley Publishing Company. (1977).
- Selvin, S. Statistical analysis of epidemiologic data. , University Press. New York: Oxford. (1996).
- Légaré, G., Hamel, D. An age-period-cohort approach to analyzing trends in suicide in Quebec between 1950 and 2009. Canadian Journal of Public Health. 104, 118-123 (2013).
- Lavanchy, D. Hepatitis B virus epidemiology, disease burden, treatment, and current and emerging prevention and control measures. Journal of Viral Hepatitis. 11, 97-107 (2004).
- Chang, M. H., et al. Universal hepatitis B vaccination in Taiwan and the incidence of hepatocellular carcinoma in children. Taiwan Childhood Hepatoma Study Group. New England Journal of Medicine. 336, 1855-1859 (1997).
- Lu, F. T., Ni, Y. H. Elimination of mother-to-infant transmission of hepatitis B virus: 35 years of experience. Pediatric Gastroenterology, Hepatology & Nutrition. 23 (4), 311-318 (2020).
- Chien, Y. C., Jan, C. F., Kuo, H. S., Chen, C. J. Nationwide hepatitis B vaccination program in Taiwan: effectiveness in the 20 years after it was launched. Epidemiologic Reviews. 28, 126-135 (2006).
- Ahmad, O. B., et al. Age standardization of rates: a new WHO standard. Geneva: GPE Discussion Paper Series. World Health Organization. , 31(2005).
- da Silva, C. P., Emídio, E. S., de Marchi, M. R. Method validation using weighted linear regression models for quantification of UV filters in water samples. Talanta. 131, 221-227 (2015).
- Dawes, R. M. The robust beauty of improper linear models in decision making. American Psychologist. 34, 571-582 (1979).
- Dawes, R. M., Corrigan, B. Linear models in decision making. Psychological Bulletin. 81, 95-106 (1974).
- Einhorn, H. J., Hogarth, R. M. Unit weighting schemes for decision making. Organizational Behavior and Human Performance. 13, 171-192 (1975).
- Wang, W., et al. Association of hepatitis B virus DNA level and follow-up interval with hepatocellular carcinoma recurrence. JAMA Network Open. 3 (4), 203707(2020).
- Holford, T. R. The estimation of age, period and cohort effects for vital rates. Biometrics. 39, 311-324 (1983).
転載および許可
このJoVE論文のテキスト又は図を再利用するための許可を申請します
許可を申請さらに記事を探す
This article has been published
Video Coming Soon
Copyright © 2023 MyJoVE Corporation. All rights reserved