Method Article
Prévision de la mortalité par carcinome hépatocellulaire à l’aide d’un modèle de régression pondérée pour estimer les effets de cohorte à Taïwan
Dans cet article
Résumé
Nous décrivons une méthode à plusieurs étapes pour mesurer un effet de cohorte avec des données sur l’âge, ce qui permet d’éliminer les données dans de nombreuses situations sans sacrifier la qualité des données. Le protocole démontre la stratégie et fournit un modèle de régression pondéré pour l’analyse des données sur le carcinome hépatocellulaire.
Résumé
Afin d’éliminer l’influence de l’âge et de la période dans les données du tableau de contingence du cycle d’âge, une méthode en plusieurs étapes a été adoptée pour évaluer l’effet de cohorte. La tumeur maligne primitive la plus générale du foie est le carcinome hépatocellulaire (CHC). Le CHC est associé à une cirrhose du foie avec des étiologies alcooliques et virales. En épidémiologie, les tendances à long terme de la mortalité du CHC ont été délimitées (ou prévues) à l’aide d’un modèle de cohorte d’âge, de période et de cohorte (APC). Les décès par CHC ont été déterminés pour chaque cohorte avec son influence pondérée. L’intervalle de confiance (IC) de la moyenne pondérée est assez étroit (comparé aux estimations équipondérées). En raison de l’IC assez étroit avec moins d’incertitude, l’estimation de la moyenne pondérée a été utilisée comme moyen de prévision. Avec la méthode à plusieurs degrés, il est recommandé d’utiliser une estimation moyenne pondérée basée sur un modèle de régression pour évaluer l’effet de cohorte dans les données du tableau de contingence âge-période.
Introduction
La tumeur maligne primitive la plus courante du foie est le carcinome hépatocellulaire (CHC). Son taux de mortalité se classe au cinquième rang chez les hommes et au huitième rang chez les femmes (6 % des hommes et 3 % des femmes) 1 parmi toutes les tumeurs malignes dans le monde. À Taïwan, c’est le cancer le plus fréquent chez les hommes et le deuxième cancer le plus fréquent chez les femmes (21,8 % des hommes et 14,2 % des femmes) 2. On estime que depuis 2000, le nombre annuel de CHC diagnostiqués dans le monde est de 564 000, dont 398 000 hommes et 166 000 femmes3. En épidémiologie, la façon la plus courante d’expliquer la relation entre les variables de l’âge, de la période et de la cohorte (APC) est que l’âge et la période s’influencent mutuellement pour créer une expérience générationnelle unique pour la tendance de la maladie étudiée.
Même si cette conceptualisation a toujours un lien linéaire précis entre l’âge et la cohorte = la période, l’exposition (prédicteur) n’est pas un facteur inhérent à une cohorte de naissance. Au lieu de cela, nous proposons que lorsque les changements entraînent des distributions différentes de la maladie, il y a un effet de cohorte. Néanmoins, puisque l’âge + la cohorte = la période, ces trois variables sont linéairement liées ; ce n’est que si d’autres restrictions sont appliquées qu’il est impossible de générer un modèle d’estimation de l’âge, de la période et de la cohorte (APC) en utilisant les effets linéaires de l’âge, de la période et de la cohorte. Dans cette étude, nous avons clarifié ce problème et les restrictions potentielles que nous avons imposées dans nos publications précédentes 4,5,6,7.
À la moindre conjecture sur les données du tableau de contingence, la méthode en plusieurs étapes 8 propose trois étapes pour évaluer l’effet de cohorte. De plus, comme le polissage médian ne dépend pas d’une distribution ou d’un cadre spécifique, il a été utilisé pour divers types de données, tels que les ratios, les rapports logarithmiques et les dénombrements. Le polissage médian est la principale technique utilisée dans la méthode multiphasique.
Les données d’un tableau de contingence à deux facteurs 9 ont été utilisées pour générer le développement de la médiane polie. La procédure de polissage de la médiane est utilisée pour éliminer les effets cumulatifs de l’âge (c’est-à-dire la rangée) et de la période (c’est-à-dire la colonne) en soustrayant itérativement la médiane de chaque ligne et de chaque colonne. Cette procédure est souvent utilisée dans l’analyse des données épidémiologiques 10. L’un des avantages de cette technique est qu’il n’est pas nécessaire d’émettre des hypothèses sur la distribution ou la structure des données dans le tableau de contingence bidirectionnel. Par conséquent, cette technique a été largement utilisée pour tout type de données contenues dans le tableau, telles que les données sur le suicide 11. Le modèle APC a également été utilisé pour décrire les tendances à long terme de l’incidence ou de la mortalité des maladies 5. Les modèles APC supposent souvent que l’âge, la période et la cohorte ont des effets additifs sur la transformation logarithmique de la maladie/mortalité. Pour évaluer les effets de cohorte, le protocole décrit génère un modèle APC pour l’analyse complète de la mortalité par carcinome hépatocellulaire (CHC) avec régression pondérée, ce qui permet des prédictions fiables et une évaluation modérée des effets du traitement.
Protocole
1. Sources des données
Pour démontrer les calculs, nous avons utilisé des données annuelles sur la mortalité par CHC de 1976 à 2015 pour les hommes et les femmes à Taïwan. Le progiciel statistique pour les sciences sociales (SPSS) version 24.0 pour Windows et Microsoft Excel a été utilisé pour exécuter les protocoles de cette étude.
- Demandez au médecin du CHC de classer les symptômes cliniques des patients, les tests de laboratoire et les résultats d’imagerie médicale afin de donner un code de diagnostic selon le code de la Classification internationale des maladies (CIM), CIM 150.
- Assurez-vous que le fichier de données (sauvegardé au format CSV) contient l’année (c.-à-d. la période), l’âge, la cohorte, le nombre de décès, le nombre de population au milieu de l’année et la mortalité sous forme de colonnes.
- Cliquez sur Fichier | Importer des données | Données CSV | Ouvrez. Assurez-vous que la case Lire les noms des variables de la première ligne des données est cochée, puis cliquez sur OK. Assurez-vous que le fichier de données est importé dans SPSS.
- Construire des données de tableau de contingence croisées par groupes d’âge-période à l’aide de SPSS. En général, nous définissons les variables de ligne comme l’âge et les variables de colonne comme la période. Si les données comportaient des données d’une seule période, d’une seule année (ou d’une seule année d’âge), il était nécessaire de les intégrer dans un groupe de périodes (ou de groupes d’âge). Ensuite, nous avons croisé les attitudes d’un groupe d’âge au cours des années d’enquête.
- Cliquez sur Analyser | Statistiques descriptives | Tableaux croisés et sélectionnez la variable d’âge dans la zone à côté de la ou des lignes et la variable de période dans la case à côté de la ou des colonnes. Cliquez sur Cellules et assurez-vous que la case Observé est cochée. Un tableau d’urgence du nombre de décès (ou du nombre de population en milieu d’année, ou de la mortalité) peut être effectué dans SPSS en procédant comme suit.
- Exportez les données du tableau de contingence qui ont été saisies au format CSV pour analyse à l’aide d’autres logiciels. Cliquez sur Fichier | Exporter des données | Assurez-vous que le format de données souhaité est au format CSV | Emplacement. Ce champ non modifiable affiche l’emplacement sécurisé du fichier exporté.
- Nom de fichier : cliquez sur Sélectionner pour modifier le nom du fichier.
- Exporter en tant que type : sélectionnez un type de fichier CSV dans le menu déroulant. Cliquez sur variables pour afficher les variables disponibles et pour sélectionner les tables de variables. Par défaut, toutes les variables de l’ensemble de données source sont conservées pour le fichier exporté. Les chercheurs peuvent utiliser les tables pour spécifier les variables sources à inclure dans le fichier exporté. Cliquez sur Exporter.
2. Réglage du modèle
REMARQUE : La méthode en plusieurs étapes a été proposée par Keys et Li 8 avec une investigation graphique. Une analyse du polissage médian a été effectuée afin d’éliminer les effets cumulatifs de l’âge et de la période ; Enfin, ces résidus de la phase de polissage médian dans la catégorie de cohorte du modèle de régression linéaire ont été régressés, et les effets de cohorte à l’aide des données du tableau de contingence ont été évalués.
- La représentation graphique comme première phase
- Créez un graphique linéaire des groupes d’âge et des groupes de périodes. Pour inspecter les cohortes de naissance de tous les groupes d’âge ou de toutes les cohortes de naissance, dessinez des cohortes de naissance paires de tous les âges ou de tous les cycles dans les graphiques linéaires.
- Importez un fichier CSV avec les données de mortalité de la table de contingence. Cliquez sur Fichier | Ouvrir | Sélectionnez un fichier CSV dans un dossier. N’oubliez pas de choisir Tous les fichiers dans la liste déroulante à côté de la zone Nom du fichier.
- Cliquez sur Ouvrir pour ouvrir le fichier CSV. Mettez en surbrillance les lignes et les colonnes des données d’urgence en matière de mortalité et cliquez sur Insérer | Graphiques | Graphique linéaire.
- L’analyse du polissage médian comme deuxième phase
- Soustrayez de manière itérative la médiane de chaque ligne et de chaque colonne pour éliminer l’effet cumulatif de l’âge et de la période. Après la phase de polissage médian, conservez les résidus pour la procédure de régression afin d’évaluer les effets de cohorte.
- Calculez le tableau médian et résiduel global. Importez un fichier CSV avec les données de mortalité du tableau de contingence (voir 2.1.1.2).
- LN a été utilisé pour chaque cellule des données de mortalité du tableau de contingence. Cliquez sur Formules | Fonction mathématique et trigonométrie et sélectionnez LN.
- Numéro : Entrez l’étiquette d’emplacement pour chaque cellule. Assurez-vous que chaque cellule des données de mortalité du tableau de contingence a pris LN. Cliquez sur Formules | Plus de fonctions | Statistiques et sélectionnez MÉDIANE.
- Numéro1 : Entrez l’étiquette d’emplacement de la première cellule.
- Numéro 2 : Entrez l’étiquette d’emplacement de la dernière cellule. Assurez-vous que la valeur médiane résultante est stockée dans la marge supérieure gauche du tableau de contingence. Assurez-vous qu’une table résiduelle est créée en prenant la différence entre la valeur d’origine (c’est-à-dire les données de mortalité LN) et la médiane globale.
- Calculez les médianes des rangées (c.-à-d. les médianes de chaque groupe d’âge) et assurez-vous qu’il a calculé les valeurs médianes des rangées pour le groupe d’âge de réponse. Cliquez sur Formules | Plus de fonctions | Statistiques | Sélectionnez MÉDIANE.
- Numéro 1 : Entrez l’étiquette de la première cellule de l’échantillon brut.
- Numéro 2 : Entrez l’étiquette de la dernière cellule de la matière première. Assurez-vous que les valeurs médianes de ligne résultantes sont stockées dans la marge de gauche de la table de contingences.
- Créez une nouvelle table résiduelle après avoir soustrait des médianes de ligne. Assurez-vous qu’un nouvel ensemble de valeurs résiduelles est créé à partir des médianes de ligne, où chaque cellule prend la valeur de la soustraction de la médiane de ligne de chaque variable de réponse de cette ligne. Cliquez sur = et assurez-vous que l’étiquette d’emplacement global de la cellule de chaque ligne a soustrait l’étiquette de la médiane de la marge de gauche.
- Calculez les médianes des colonnes (c’est-à-dire les médianes de chaque groupe de périodes) et assurez-vous qu’il calcule les valeurs médianes des colonnes pour le groupe de périodes de réponse. Cliquez sur Formules | Plus de fonctions | Statistiques | Sélectionnez MÉDIANE.
- Numéro 1 : Entrez le premier libellé d’emplacement de cellule de la colonne. Numéro 2 : Entrez le dernier libellé d’emplacement de cellule de la colonne. Assurez-vous que les valeurs médianes de colonne résultantes sont stockées dans la marge supérieure de la table de contingence.
- Créez une nouvelle table résiduelle après avoir soustrait des médianes de colonne. Assurez-vous qu’un nouvel ensemble de valeurs résiduelles est créé à partir des médianes de colonne, où chaque cellule prend la valeur de la soustraction de la médiane de colonne de chaque variable de réponse de cette colonne. Cliquez sur = et assurez-vous que l’étiquette d’emplacement de la cellule globale de chaque colonne a soustrait l’étiquette de la médiane de la marge supérieure.
- Répétez les étapes 2.1.2.7 à 2.1.2.10 jusqu’à ce que les médianes des lignes et des colonnes soient proches de zéro. Cliquez sur Formules | Plus de fonctions | Statistiques | Sélectionnez MÉDIANE. Assurez-vous que les médianes des lignes et des colonnes sont approximativement nulles. Enregistrez le tableau résiduel final au format CSV.
- Procédure de régression avec le poids comme troisième phase
REMARQUE : Nous avons calculé la variable dépendante sous forme de résidus pour chaque cohorte avec le nombre de décès comme poids. Ensuite, nous avons effectué des régressions linéaires pour calculer les effets de cohorte.- Assurez-vous que Kutools pour Excel a été installé et utilisez son outil Transposer les dimensions du tableau pour convertir rapidement les tableaux croisés en listes plates. Importez un fichier CSV avec les données résiduelles de la table de contingence (voir 2.1.2.11).
- Sélectionnez la table à convertir en liste. Cliquez sur le bouton Kutools | Modifier | Transposer la dimension de la table. Dans la boîte de dialogue Transposer les dimensions de la table, assurez-vous que la case en regard de la liste Table croisée à sélectionner est cochée et sélectionnez la plage Résultats pour stocker les valeurs résiduelles au format de liste.
- Insérer dans le fichier de données initial une colonne (voir 1.2) avec les données résiduelles du format de liste (voir 2.1.3.1). Assurez-vous qu’il a inséré une colonne de support dans les données du format de liste résiduelle (reportez-vous à 2.1.3.1). Cliquez sur = variables d’âge et de période, puis cliquez sur Entrée. Utilisez une colonne de support pour rechercher les étiquettes de groupe d’âge et de période des données de format de liste résiduelle pour insérer une colonne résiduelle de réponse dans le fichier de données initial (reportez-vous à 1.2).
- Cliquez sur Formules | Recherche et référence | Sélectionnez RECHERCHEV. Définissez VLOOKUP (étiquette d’emplacement de cellule d’âge et d’emplacement de cellule de la période, première étiquette d’emplacement de cellule de la colonne de support : l’étiquette de la dernière cellule de la colonne résiduelle, 4, 0). Assurez-vous que la plage sélectionnée comprend les colonnes de support, d’âge, de période et résiduelles (c’est-à-dire la 4ecolonne en tant que liste résiduelle).
- Assurez-vous que les résidus sont insérés dans le fichier de données initial (reportez-vous à la section 1.2) et recherchez les données du format de liste résiduelle (reportez-vous à la section 2.1.3.1) pour l’étape suivante. Ajustez le modèle de régression à l’aide des moindres carrés non pondérés et analysez les résidus.
- Cliquez sur Analyser | Régression | Linéaire. Transférez la variable indépendante, catégorie de cohorte (c.-à-d. 17 cohortes de naissance), dans la case Indépendant(s) et la variable dépendante, Résidus, dans la case Dépendant :. Cliquez sur OK. Assurez-vous de générer les résultats des effets de cohorte non pondérés.
- Assurez-vous que les valeurs résiduelles sont insérées dans le fichier de données Excel initial (reportez-vous à la section 1.2) et recherchez les données du format de liste résiduelle (reportez-vous à la section 2.1.3.1) pour l’étape suivante. Ajustez le modèle de régression par les moindres carrés pondérés et analysez les résidus. Cliquez sur Analyser | Régression | Linéaire.
- Transférez la variable indépendante et la catégorie de cohorte (c.-à-d. 17 cohortes de naissance) dans la case « indépendant » et la variable dépendante et les résidus dans la case « dépendant : ». Transférez le numéro de décès dans la case de poids WLS. Cliquez sur OK. Assurez-vous qu’il génère les résultats de la moyenne pondérée de l’effet de cohorte.
Résultats
Les données sur la mortalité ont été présentées pour 10 groupes d’âge de cinq ans (40-44 ans, 45-49, 50-54, 55-59, 60-64, 65-69, 70-74, 75-79, 80-84 et 85+) et 8 périodes de cinq ans (1976-1980, 1981-1985, 1986-1990, 1991-1995, 1996-2000, 2001-2005, 2006-2010 et 2011-2015). Le nombre de groupes de cohortes a été sélectionné en soustrayant un du nombre total de groupes d’âge-périodes : 10 (groupes d’âge de cinq ans) + 8 (périodes de cinq ans) -1 = 17 cohortes de naissance, les groupes de cohortes de naissance étant désignés par les années de milieu de cohorte comme 1891, 1896, 1901, 1906, 1911, 1916, 1921, 1926, 1931, 1936, 1941, 1946, 1951, 1956, 1961, 1966 et 1971. Nous fournissons un format de la contingence du groupe d’âge des hommes et des femmes atteints de CHC (dans le tableau supplémentaire 1). Les figures 1 et 2 montrent les taux de mortalité du CHC dans les groupes d’âge et de période. Ces fluctuations étaient plus importantes chez les hommes que chez les femmes. Le rapport basé sur la répartition par âge montre qu’à l’extrémité inférieure de la tranche d’âge des 40-44 ans, les taux de mortalité du CHC augmentent (figure 1). En revanche, la figure 2 montre clairement que les taux de mortalité du CHC ont progressivement augmenté dans le groupe d’âge des ≥ 60 ans. Cependant, les taux de mortalité des CHC fondés sur l’âge ont considérablement changé au fil du temps, ce qui signifie qu’un effet de cohorte remarquable caché dans la table de la statistique de l’état civil normalement classifiée par âge et période ne deviendra apparent qu’à un moment donné dans l’avenir.
Nous avons mis en œuvre la procédure de polissage médian sur les taux de mortalité du CHC transformé en log. Les effets de cohorte estimés pour le modèle APC des taux de mortalité du CHC chez les hommes et les femmes sont présentés dans les tableaux 1 et 2, respectivement. De plus, les tableaux 1 et 2 présentent le calcul des deux méthodes de moyenne pondérée selon le sexe avant d’obtenir les estimations pondérées. Les estimations pondérées sont plus conformes aux données que les effets de cohorte estimés précédents, en fonction de l’écart minimal (comparaison d’estimations équipondérées) de l’intervalle de confiance (IC) des estimations pondérées.
Pour les hommes, la partie gauche du tableau 1 montre les effets des cohortes de naissance. L’effet de cohorte passe de 0,73 (l’effet de cohorte le plus précoce en 1891) à 1,20 (effet de cohorte le plus important en 1936). Chez les femmes, l’effet de cohorte passe de 0,68 (l’effet de cohorte le plus précoce en 1891) à 1,35 (effet de cohorte le plus important en 1936). Il est important de souligner que, comparativement à la cohorte de 1891, l’effet de cohorte chez les hommes et les femmes a augmenté d’environ 64 % et 98 %, respectivement. L’augmentation a été répartie également dans la partie droite du tableau 2. Ici, l’effet de cohorte est passé de 0,71 (l’effet de cohorte le plus précoce en 1891) à 1,11 (l’effet de cohorte le plus important en 1936). Chez les femmes, un effet similaire de l’augmentation de la distribution est démontré dans la colonne de droite du tableau 2. L’effet de cohorte est passé de 0,64 (l’effet de cohorte le plus précoce en 1891) à 1,11 (l’effet de cohorte le plus important en 1926). Par conséquent, par rapport à la première cohorte d’hommes et de femmes, nous avons observé une augmentation des taux de mortalité d’environ 57 % et 73 %, respectivement.
Parmi les cohortes de naissance, les hommes nés vers 1936 présentaient le risque le plus élevé de mortalité par CHC (tableau supplémentaire 1). Par conséquent, pour les estimations pondérées, l’impact de la cohorte de naissance en 1936 par rapport à celui de la cohorte de naissance de référence en 1921 était de 1,11 (IC à 95 % : 1,08-1,14). En revanche, la cohorte précédente de 1891 a montré une tendance à la forte hausse. De plus, les effets se sont inversés après la cohorte de 1936. Dans le tableau 1, par rapport à la cohorte de naissance de référence de 1916, l’effet pondéré était de 1,11 (IC à 95 % : 1,07-1,16). De plus, avec des hommes et des femmes, nous avons modélisé des effets de cohorte équipondérés et pondérés, respectivement, avec des intervalles de confiance à 95 %. Les deux figures montrent que les effets de cohorte équipondérés sont plus larges que presque toutes les largeurs des IC à 95 %.
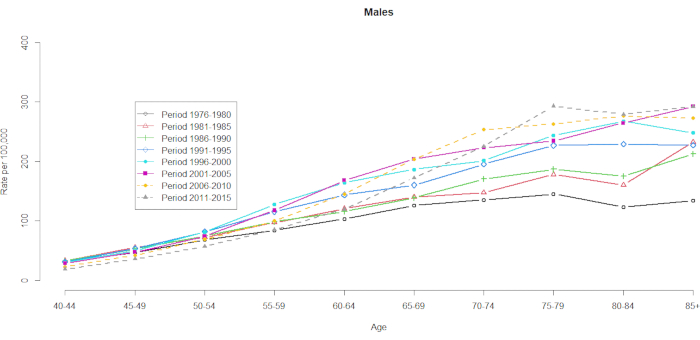
Graphique 1. Taux de mortalité par CHC pour 100 000 par âge et par période, hommes, Taïwan, 1976-2015. Veuillez cliquer ici pour voir une version agrandie de cette figure.
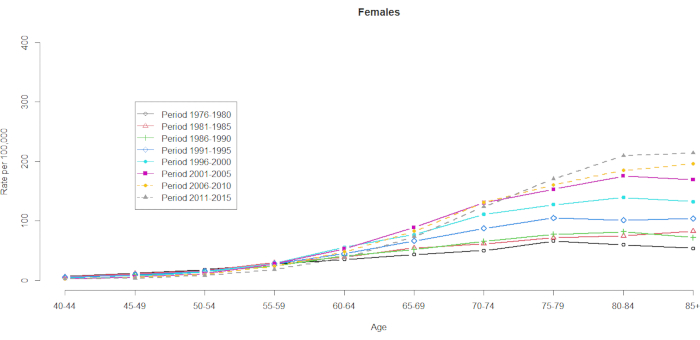
Graphique 2. Taux de mortalité par CHC pour 100 000 habitants, par âge et par période, femmes, Taïwan, 1976-2015. Veuillez cliquer ici pour voir une version agrandie de cette figure.
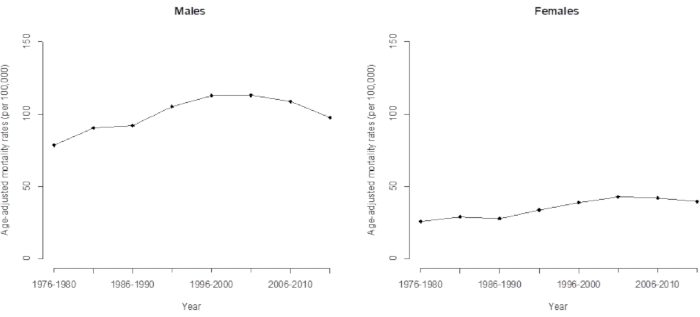
Graphique 3. Taux de mortalité ajusté selon l’âge par carcinome hépatocellulaire chez les hommes et les femmes à Taïwan. Veuillez cliquer ici pour voir une version agrandie de cette figure.
| Non lesté | Pondéré | |||
| Effets | IC à 95 % pour les effets | Effets | IC à 95 % pour les effets | |
| Cohorte | ||||
| (1891~1971) | ||||
| 1891 | 0.73 | 0.59-0.90 | 0.71 | 0.57- 0.88 |
| 1896 | 0.88 | 0.79-0.99 | 0.87 | 0.78- 0.97 |
| 1901 | 0.89 | 0.83-0.96 | 0.81 | 0.71- 0.92 |
| 1906 | 0.91 | 0.86- 0.97 | 0.85 | 0.78- 0.94 |
| 1911 | 0.95 | 0.90-1.00 | 0.89 | 0.83- 0.96 |
| 1916 | 1.01 | 0.97-1.06 | 0.99 | 0.95- 1.03 |
| 1921 | 1 | REF | 1 | REF |
| 1926 | 1.04 | 1.00-1.08 | 1.03 | 1.01- 1.06 |
| 1931 | 1.1 | 1.06-1.14 | 1.08 | 1.06- 1.11 |
| 1936 | 1.2 | 1.15- 1.24 | 1.11 | 1.08- 1.14 |
| 1941 | 1.14 | 1.09- 1.19 | 1.1 | 1.07- 1.13 |
| 1946 | 1.04 | 1.00-1.09 | 1.06 | 1.04- 1.09 |
| 1951 | 0.91 | 0.87-0.96 | 1 | 0.98- 1.03 |
| 1956 | 0.87 | 0.82-0.92 | 0.96 | 0.93- 0.98 |
| 1961 | 0.82 | 0.76-0.88 | 0.88 | 0.85- 0.92 |
| 1966 | 0.76 | 0.68- 0.85 | 0.79 | 0.74- 0.83 |
| 1971 | 0.71 | 0.57-0.87 | 0.83 | 0.80- 0.87 |
| Remarque : REF = référence ; IC = intervalle de confiance. | ||||
Tableau 1. Estimation des rapports de taux et des intervalles de conférence à 95 % pour l’effet de la cohorte de naissance sur la mortalité par carcinome hépatocellulaire chez les hommes à Taïwan, 1891-1971.
| Non lesté | Pondéré | |||
| Effets | IC à 95 % pour les effets | Effets | IC à 95 % pour les effets | |
| Cohorte | ||||
| (1891~1971) | ||||
| 1891 | 0.68 | 0.42- 1.10 | 0.64 | 0.38-1.09 |
| 1896 | 0.81 | 0.63-1.04 | 0.75 | 0.56- 1.00 |
| 1901 | 0.8 | 0.67- 0.95 | 0.7 | 0.52- 0.94 |
| 1906 | 0.83 | 0.72- 0.95 | 0.76 | 0.65- 0.88 |
| 1911 | 0.88 | 0.78- 0.99 | 0.85 | 0.78- 0.93 |
| 1916 | 1 | REF | 1 | REF |
| 1921 | 1.12 | 1.01-1.24 | 1.08 | 1.03- 1.13 |
| 1926 | 1.29 | 1.17-1.42 | 1.11 | 1.07- 1.12 |
| 1931 | 1.3 | 1.18-1.43 | 1.1 | 1.05- 1.15 |
| 1936 | 1.35 | 1.22-1.49 | 1.1 | 1.04- 1.14 |
| 1941 | 1.19 | 1.07-1.32 | 1.09 | 1.03-1.13 |
| 1946 | 1.05 | 0.94-1.17 | 1.06 | 1.02-1.11 |
| 1951 | 0.83 | 0.73-0.94 | 1 | 0.96-1.05 |
| 1956 | 0.67 | 0.58-0.77 | 0.93 | 0.89-0.98 |
| 1961 | 0.58 | 0.49-0.70 | 0.79 | 0.74-0.84 |
| 1966 | 0.59 | 0.46-0.75 | 0.58 | 0.49-0.69 |
| 1971 | 0.63 | 0.40-1.02 | 0.64 | 0.58-0.72 |
| Remarque : REF = référence ; IC = intervalle de confiance. | ||||
Tableau 2. Estimation des rapports de taux et des intervalles de conférence à 95 % pour l’effet de la cohorte de naissance sur la mortalité par carcinome hépatocellulaire chez les femmes à Taïwan, 1891-1971.
Tableau supplémentaire 1. Veuillez cliquer ici pour télécharger ce tableau.
Discussion
En raison de la tendance temporelle de la mortalité du CHC, les modèles conventionnels sous-estiment certaines caractéristiques importantes cachées dans les données (telles que les effets de cohorte), et les analyses conventionnelles qui utilisent une simple extrapolation linéaire du taux de correction logarithmique de l’âge observé montrent une précision significativement réduite dans leurs prédictions. Il est clair que cette tendance s’est poursuivie pendant 35 ans et qu’elle va suivre une tendance à la hausse dans les prochaines années si l’on observe directement la tendance à long terme de la mortalité par CHC à Taïwan de 1976 à 2015 (Figure 3). En effet, la tendance récente de la mortalité par CHC à Taïwan est à la baisse et est due à l’effet de cohorte (déterminé par l’analyse APC), qui, comme mentionné précédemment, a diminué après la cohorte de 1936. Cette étude montre que l’application du modèle APC fournit des avertissements avancés et plus précis sur les changements de tendance.
D’un point de vue clinique, environ deux milliards de personnes sont infectées par le virus de l’hépatite B (VHB) 12, et environ 350 millions de personnes en souffrent. Par conséquent, il s’agit d’un problème de santé important avec une morbidité élevée dans le monde entier. L’infection par le VHB provoque un large éventail de problèmes cliniques, notamment un statut de porteur inefficace pour fulminer l’hépatite, la cirrhose ou le carcinome hépatocellulaire. La méthode de prévention la plus efficace consiste à inoculer le vaccin contre l’hépatite B. Taïwan a mis en œuvre le premier plan mondial de vaccination de masse contre l’hépatite B en 1984 13. Dans le cadre de ce programme, les femmes enceintes ont été dépistées pour l’antigène de surface de l’hépatite B (HBsAg) et l’antigène d’enveloppe de l’hépatite B (HBeAg) 14. Pendant les deux premières années de ce programme, le programme d’immunisation ne couvrait que les bébés de mères atteintes d’HBsAg. Cependant, à partir de la troisième année du programme de vaccination, tous les bébés étaient couverts. Le taux de couverture du vaccin contre l’hépatite B a atteint 99 % ces dernières années 15. Près de 90 % à 95 % des personnes connaîtront une immunité à vie après avoir reçu les trois doses du vaccin. Nous soulignons que le déclin du CHC pédiatrique à Taïwan est largement attribué à ce programme mondial de vaccination.
La modélisation APC décrite dans cet article fournit un avertissement préalable sur ces changements de tendance (accrus) (qui diminueront dans un avenir proche). Lorsque l’on compare la tendance des effets de cohorte (tableaux 1 et 2) et de la mortalité ajustée selon l’âge (figure 3), le taux de mortalité ajusté directement selon l’âge (ou taux de mortalité normalisé selon l’âge) était le même que la moyenne pondérée. Il pondère les taux de mortalité selon l’âge en fonction de la proportion du groupe d’âge d’intérêt sur la base de la population standard mondiale de 2000 16 dans cette étude. Comme la validation des effets de cohorte dominait le dernier schéma de mortalité du CHC, nous avons calculé la mortalité du CHC ajustée selon l’âge pour les données à jour (jusqu’en 2011-2015). Nous avons interprété cela comme signifiant que l’estimation moyenne pondérée des cohortes fournit des informations fiables pendant que la recherche est prête à prévoir la mortalité future du CHC. Des détails sur la prévision de la mortalité du CHC sont disponibles dans notre étude précédente 5.
Une hypothèse générale est que chaque valeur dans les données fournit des informations égales pour évaluer les paramètres d’un modèle. Cette approche a été utilisée dans la plupart des méthodes de modélisation (telles que les modèles de régression linéaire ou non linéaire) et signifie que l’écart-type du terme d’erreur est la variable prédictive sous-jacente constante. Cependant, d’après notre revue de littérature, cette hypothèse n’est pas adaptée à une modélisation pour estimer empiriquement des paramètres. Les paramètres inconnus sont estimés lorsque nous utilisons la régression pondérée, qui génère un poids plus petit avec moins de précision pour les points de données et un poids élevé avec plus de précision pour les points de données. Le processus de pondération a diminué l’écart-type de l’estimateur. Néanmoins, les lacunes de la méthode de régression pondérée sont presque inconnues dans la pratique empirique. Comme les poids exacts ne sont pas connus, les poids estimés ont été utilisés pour estimer les paramètres. En outre, l’expérience antérieure a montré que la pondération basée sur l’estimation ne change pas de manière significative ou affecte généralement l’analyse de régression ou son interprétation 17. Hypothétiquement, le modèle APC peut être ajusté à n’importe quelle maladie dont l’incidence est affectée par l’âge, la période et la cohorte. De plus, des estimations moyennes pondérées ont été mises à disposition pour la prédiction 18,19,20. Si l’IC est relativement étroit, l’incertitude est faible. Compte tenu du fait que l’IC représente l’incertitude inhérente à ce type d’évaluation et les valeurs qu’il contient, nous concluons généralement que l’utilisation de l’IC a un impact substantiel.
La chimioembolisation artérielle transcathéter (TACE) est l’une des méthodes les plus efficaces pour contrôler cliniquement le CHC. Cependant, il est difficile de choisir cette méthode comme traitement principal ou auxiliaire, car elle ne nécessite pas de chirurgie ouverte. Le foie fournit généralement 75 % du sang et des nutriments par la veine porte hépatique, tandis que l’artère hépatique fournit 25 % du sang et des nutriments. Contrairement au sang de l’artère hépatique extrait de la plupart des CHC, ce liquide augmente rapidement et provient rarement de la veine porte hépatique. De plus, cet effet est bien adapté à la TACE car le cancer primitif du foie métastase rarement dans d’autres parties du corps. Même s’il est peu probable que les tumeurs malignes hépatocellulaires métastasent, elles sont difficiles à éradiquer. En pratique clinique, le suivi des patients atteints de CHC est effectué tous les deux à trois mois. Une fois qu’une élévation anormale de l’alpha-fœtoprotéine (AFP) ou un contrôle échographique anormal est détecté, une tomodensitométrie et une imagerie par résonance magnétique sont effectuées. Si une nouvelle tumeur est découverte, la TACE sera prise en compte. De nouveaux biomarqueurs ont également été développés pour détecter la récurrence du CHC lié au VHB, tels que l’indice quantitatif de temps de l’ADN du VHB (HDQTI) 21. Le produit des résultats de suivi et du logarithme du rapport de charge d’ADN du VHB détecté à la charge normale est la somme des HDQTI. Le HDQTI est utilisé comme indicateur pronostique indépendant de la récurrence du CHC lié au VHB 21.
Notre étude présente plusieurs limites. Tout d’abord, nous avons simplement émis des hypothèses concernant les étiologies des changements observés. À l’aide du modèle APC, la mortalité du CHC en fonction de l’âge, de la période et des effets de cohorte a été reconsidérée. Néanmoins, dans cette étude, nous avons utilisé le réglage médian de polissage comme hypothèse. Deuxièmement, l’analyse APC a été largement utilisée dans le domaine de l’épidémiologie dans les pays en développement ou récemment développés pour des études de cohorte à long terme. Troisièmement, nous ne disposions pas d’informations provenant de l’ensemble de données de format accumulées pour ajuster les facteurs de confusion dans le modèle APC, tels que les comorbidités ou le mode de vie. Des données isolées sont nécessaires pour les recherches futures afin de résoudre cette limitation. Quatrièmement, pour modifier la procédure de régression dans la méthode à plusieurs étapes, nous avons utilisé le nombre de décès dus au CHC comme poids. Comme le poids exact n’est pas connu, l’utilisation de divers poids provoque une légère inflation au sein des effets de cohorte estimés. En fin de compte, il existe différentes méthodes d’estimation APC pour résoudre le problème méconnaissable (par exemple, Holford utilise des tendances linéaires et de courbure pour résoudre le problème méconnaissable 22). Dans le même temps, le polissage médian fournit des hypothèses complexes sous la forme d’une conversion conceptuelle entre les modèles APC pour évaluer l’effet de cohorte avec le moins d’hypothèses possible et applique facilement un format commun pour les tableaux de contingence.
Dans l’ensemble, l’effet moyen pondéré avec un IC comparativement étroit de chaque cohorte a ensuite été autorisé par l’estimation pondérée à modifier le modèle de régression. En bref, pour les méthodes à plusieurs degrés, il est conseillé d’utiliser des estimations pondérées des modèles de régression pour évaluer les effets de cohorte dans les données des tableaux de contingence âge-période.
Déclarations de divulgation
Les auteurs n’ont rien à divulguer.
Remerciements
Ce travail a été soutenu par l’hôpital Taipei Tzu Chi TCRD-TPE-109-RT-8 (2/3) et TCRD-TPE-109-39 (2/2).
matériels
| Name | Company | Catalog Number | Comments |
| not applicable | not applicable | not applicable | not applicable |
Références
- Kuntz, E., Kuntz, H. D. Hepatology: Principles and Practice. , Springer. New York. 774(2006).
- McGlynn, K. A., et al. International trends and patterns of primary liver cancer. International Journal of Cancer. 94 (2), 290-296 (2001).
- Bosch, F. X., Ribes, J., Diaz, M., Cleries, R. Primary liver cancer: worldwide incidence and trends. Gastroenterology. 127, 5-16 (2004).
- Tzeng, I. S., Ng, C. Y., Chen, J. Y., Chen, L. S., Wu, C. C. Using weighted regression model for estimating cohort effect in age-period contingency table data. Oncotarget. 9 (28), 19826-19835 (2018).
- Tzeng, I. S., Lee, W. C. Forecasting hepatocellular carcinoma mortality in Taiwan using an age-period-cohort model. Asia-Pacific Journal of PublicHealth. 27, 65-73 (2015).
- Tzeng, I. S., et al. Predicting emergency departments visit rates from septicemia in Taiwan using an age-period-cohort model, 1998 to 2012. Medicine. 95, 5598(2016).
- Chen, S. H., et al. Period and Cohort Analysis of Rates of Emergency Department Visits Due to Pneumonia in Taiwan, 1998-2012. Risk Management and Healthcare Policy. 13, 1459-1466 (2020).
- Keyes, K. M., Li, G. A multiphase method for estimating cohort effects in age-period contingency table data. Annals of Epidemiology. 20, 779-785 (2010).
- Tukey, J. Exploratory data analysis Reading: MS. , Addison-Wesley Publishing Company. (1977).
- Selvin, S. Statistical analysis of epidemiologic data. , University Press. New York: Oxford. (1996).
- Légaré, G., Hamel, D. An age-period-cohort approach to analyzing trends in suicide in Quebec between 1950 and 2009. Canadian Journal of Public Health. 104, 118-123 (2013).
- Lavanchy, D. Hepatitis B virus epidemiology, disease burden, treatment, and current and emerging prevention and control measures. Journal of Viral Hepatitis. 11, 97-107 (2004).
- Chang, M. H., et al. Universal hepatitis B vaccination in Taiwan and the incidence of hepatocellular carcinoma in children. Taiwan Childhood Hepatoma Study Group. New England Journal of Medicine. 336, 1855-1859 (1997).
- Lu, F. T., Ni, Y. H. Elimination of mother-to-infant transmission of hepatitis B virus: 35 years of experience. Pediatric Gastroenterology, Hepatology & Nutrition. 23 (4), 311-318 (2020).
- Chien, Y. C., Jan, C. F., Kuo, H. S., Chen, C. J. Nationwide hepatitis B vaccination program in Taiwan: effectiveness in the 20 years after it was launched. Epidemiologic Reviews. 28, 126-135 (2006).
- Ahmad, O. B., et al. Age standardization of rates: a new WHO standard. Geneva: GPE Discussion Paper Series. World Health Organization. , 31(2005).
- da Silva, C. P., Emídio, E. S., de Marchi, M. R. Method validation using weighted linear regression models for quantification of UV filters in water samples. Talanta. 131, 221-227 (2015).
- Dawes, R. M. The robust beauty of improper linear models in decision making. American Psychologist. 34, 571-582 (1979).
- Dawes, R. M., Corrigan, B. Linear models in decision making. Psychological Bulletin. 81, 95-106 (1974).
- Einhorn, H. J., Hogarth, R. M. Unit weighting schemes for decision making. Organizational Behavior and Human Performance. 13, 171-192 (1975).
- Wang, W., et al. Association of hepatitis B virus DNA level and follow-up interval with hepatocellular carcinoma recurrence. JAMA Network Open. 3 (4), 203707(2020).
- Holford, T. R. The estimation of age, period and cohort effects for vital rates. Biometrics. 39, 311-324 (1983).
Réimpressions et Autorisations
Demande d’autorisation pour utiliser le texte ou les figures de cet article JoVE
Demande d’autorisationThis article has been published
Video Coming Soon