Method Article
Vorhersage der Mortalität des hepatozellulären Karzinoms unter Verwendung eines gewichteten Regressionsmodells zur Abschätzung von Kohorteneffekten in Taiwan
In diesem Artikel
Zusammenfassung
Wir stellen eine mehrstufige Methode dar, um einen Kohorteneffekt mit Altersdaten zu messen, wodurch Daten in vielen Situationen eliminiert werden können, ohne die Datenqualität zu beeinträchtigen. Das Protokoll demonstriert die Strategie und bietet ein gewichtetes Regressionsmodell für die Analyse der hepatozellulären Karzinomdaten.
Zusammenfassung
Um den Einfluss von Alter und Zeitraum auf die Kontingenztabellen des Alterszyklus zu eliminieren, wurde eine mehrstufige Methode zur Bewertung des Kohorteneffekts angewendet. Der häufigste primäre bösartige Tumor der Leber ist das hepatozelluläre Karzinom (HCC). HCC ist mit Leberzirrhose mit Alkohol und viralen Ätiologien assoziiert. In der Epidemiologie wurden langfristige Trends der HCC-Mortalität mit Hilfe eines Alters-Perioden-Kohortenmodells (APC) skizziert (bzw. prognostiziert). Die HCC-Todesfälle wurden für jede Kohorte mit ihrem gewichteten Einfluss bestimmt. Das Konfidenzintervall (CI) des gewichteten Mittelwerts ist relativ eng (im Vergleich zu den gleichgewichteten Schätzungen). Aufgrund des relativ engen KI mit geringerer Unsicherheit wurde die gewichtete mittlere Schätzung als Mittel für die Prognose verwendet. Bei der mehrstufigen Methode empfiehlt es sich, eine gewichtete Mittelwertschätzung auf Basis eines Regressionsmodells zu verwenden, um den Kohorteneffekt in den Daten der Altersperioden-Kontingenztabelle zu bewerten.
Einleitung
Der häufigste primäre bösartige Tumor der Leber ist das hepatozelluläre Karzinom (HCC). Die Sterblichkeitsrate liegt bei Männern an fünfter Stelle und bei Frauen an achter Stelle (6 % der Männer und 3 % der Frauen) 1 unter allen bösartigen Tumoren weltweit. In Taiwan ist es die häufigste Krebserkrankung bei Männern und die zweithäufigste Krebserkrankung bei Frauen (21,8 % der Männer und 14,2 % der Frauen) 2. Es wird geschätzt, dass seit dem Jahr 2000 weltweit jährlich 564.000 HCCs diagnostiziert wurden, davon 398.000 Männer und 166.000 Frauen 3. In der Epidemiologie ist die gebräuchlichste Methode, die Beziehung zwischen Alters-, Perioden- und Kohortenvariablen (APC) zu erklären, dass Alter und Periode sich gegenseitig beeinflussen, um eine einzigartige Generationserfahrung für den untersuchten Krankheitstrend zu schaffen.
Auch wenn diese Konzeptualisierung immer noch einen präzisen linearen Zusammenhang von Alter + Kohorte = Periode hat, ist die Exposition (Prädiktor) kein inhärenter Faktor in einer Geburtskohorte. Stattdessen schlagen wir vor, dass, wenn Veränderungen unterschiedliche Krankheitsverteilungen verursachen, es einen Kohorteneffekt gibt. Da Alter + Kohorte = Zeitraum jedoch sind, sind diese drei Variablen linear miteinander verknüpft; Nur wenn andere Einschränkungen durchgesetzt werden, ist es unmöglich, ein geschätztes Alters-Perioden-Kohortenmodell (APC) unter Verwendung der linearen Effekte von Alter, Zeitraum und Kohorte zu erstellen. In dieser Studie haben wir diese Problematik und die möglichen Einschränkungen, die wir in unseren früheren Publikationen auferlegt haben 4,5,6,7, geklärt.
Mit den geringsten Vermutungen über die Daten der Kontingenztabelle bietet die mehrstufige Methode 8 drei Stufen zur Bewertung des Kohorteneffekts. Da die Medianpolitur nicht von einer bestimmten Verteilung oder einem bestimmten Rahmen abhängt, wurde sie für verschiedene Datentypen verwendet, z. B. Verhältnisse, logarithmische Verhältnisse und Anzahl. Das Medianpolieren ist die wichtigste Technik, die bei der Mehrphasenmethode verwendet wird.
Daten aus einer bidirektionalen Kontingenztabelle 9 wurden verwendet, um die Entwicklung des polierten Medians zu generieren. Das Verfahren zum Polieren des Medians wird verwendet, um die kumulativen Effekte von Alter (d. h. Zeile) und Periode (d. h. Spalte) zu eliminieren, indem der Median iterativ von jeder Zeile und jeder Spalte subtrahiert wird. Dieses Verfahren wird häufig in der epidemiologischen Datenanalyse eingesetzt 10. Ein Vorteil dieser Technik besteht darin, dass keine Annahmen über die Verteilung oder Struktur der Daten in der bidirektionalen Kontingenztabelle erforderlich sind. Daher wurde diese Technik in großem Umfang für alle Arten von Daten verwendet, die in der Tabelle enthalten sind, wie z. B. Suiziddaten 11. Das APC-Modell wurde auch verwendet, um die langfristigen Trends der Krankheitsinzidenz oder Mortalität zu beschreiben 5. APC-Modelle gehen oft davon aus, dass Alter, Periode und Kohorte additive Effekte auf die logarithmische Transformation von Krankheit/Mortalität haben. Um Kohorteneffekte zu evaluieren, generiert das beschriebene Protokoll ein APC-Modell für die vollständige Mortalitätsanalyse des hepatozellulären Karzinoms (HCC) mit gewichteter Regression, wodurch zuverlässige Vorhersagen und eine moderate Bewertung der Behandlungseffekte unterstützt werden.
Protokoll
1. Datenquellen
Um die Berechnungen zu veranschaulichen, verwendeten wir jährliche Daten zur HCC-Mortalität von 1976 bis 2015 für Männer und Frauen in Taiwan. Für die Ausführung der Protokolle für diese Studie wurden das Statistical Package for Social Sciences (SPSS) Version 24.0 für Windows und Microsoft Excel verwendet.
- Lassen Sie den HCC-Arzt die klinischen Symptome der Patienten, Labortests und medizinische Bildgebungsergebnisse klassifizieren, um einen Diagnosecode gemäß dem Code der Internationalen Klassifikation der Krankheiten (ICD), ICD 150, zu erhalten.
- Stellen Sie sicher, dass die Datendatei (die als CSV gespeichert wird) das Jahr (d. h. den Zeitraum), das Alter, die Kohorte, die Sterbezahl, die Bevölkerungszahl zur Jahresmitte und die Sterblichkeit als Spalten enthält.
- Klicken Sie auf Datei | Daten importieren | CSV-Daten | Öffnen. Stellen Sie sicher, dass das Kontrollkästchen neben Variablennamen aus der ersten Zeile der Daten lesen aktiviert ist, und klicken Sie auf OK. Stellen Sie sicher, dass die Datendatei in SPSS importiert wird.
- Erstellen Sie Kontingenztabellendaten, die über SPSS nach Altersgruppen gekreuzt werden. Im Allgemeinen haben wir Zeilenvariablen als Alter und Spaltenvariablen als Zeitraum definiert. Wenn es sich bei den Daten um Daten für ein einzelnes Periodenjahr (oder ein einzelnes Altersjahr) handelte, war es notwendig, diese in eine Periodengruppe (oder Altersgruppe) zu integrieren. Dann haben wir die Einstellungen zu einer Altersgruppe über die Erhebungsjahre hinweg kreuztabellarisch dargestellt.
- Klicken Sie auf Analysieren | Deskriptive Statistik | Kreuztabellen und wählen Sie die Variable "Alter" im Feld neben der Zeile(n) und die Variable "Zeitraum" im Feld neben der Spalte(n) aus. Klicken Sie auf Zellen und vergewissern Sie sich, dass das Kontrollkästchen neben Beobachtet aktiviert ist. Eine Kontingenztabelle der Sterbezahl (oder der Bevölkerungszahl zur Jahresmitte oder der Sterblichkeit) kann in SPSS mit den oben genannten Schritten erstellt werden.
- Exportieren Sie die Daten der Kontingenztabelle, die im CSV-Format eingegeben wurden, für die Analyse mit anderer Software. Klicken Sie auf Datei | Daten exportieren | Gewünschtes Datenformat als CSV sicherstellen | Standort. Dieses nicht bearbeitbare Feld zeigt den sicheren Speicherort für die exportierte Datei an.
- Dateiname: Klicken Sie auf Auswählen , um den Dateinamen zu ändern.
- Als Typ exportieren: Wählen Sie einen CSV-Dateityp aus dem Dropdown-Menü aus. Klicken Sie auf Variablen , um die verfügbaren Variablen anzuzeigen und die Variablentabellen auszuwählen. Standardmäßig werden alle Variablen aus dem Quelldatensatz für die exportierte Datei beibehalten. Forscher können die Tabellen verwenden, um anzugeben, welche Quellvariablen in die exportierte Datei aufgenommen werden sollen. Klicken Sie auf Exportieren.
2. Modell-Einstellung
HINWEIS: Die mehrstufige Methode wurde von Keys und Li 8 mit grafischer Untersuchung vorgeschlagen. Es wurde eine mediane Polituranalyse durchgeführt, um die kumulativen Auswirkungen von Alter und Periode auszuschließen; Schließlich wurden diese Residuen aus der medianen polnischen Phase in der Kohortenkategorie im linearen Regressionsmodell regressiert und Kohorteneffekte anhand von Daten in der Kontingenztabelle bewertet.
- Grafische Darstellung als erste Phase
- Erstellen Sie ein Liniendiagramm der Altersgruppen und Periodengruppen. Um Geburtskohorten über Altersgruppen oder Geburtskohorten hinweg zu untersuchen, zeichnen Sie in den Liniendiagrammen gleichmäßige Geburtskohorten über Altersgruppen oder Zyklen hinweg.
- Importieren Sie eine CSV-Datei mit Sterbedaten aus der Kontingenztabelle. Klicken Sie auf Datei | Öffnen | Navigieren Sie zu einer CSV-Datei aus einem Ordner, um sie auszuwählen. Denken Sie daran, Alle Dateien in der Dropdown-Liste neben dem Feld Dateiname auszuwählen.
- Klicken Sie auf Öffnen , um die CSV-Datei zu öffnen. Markieren Sie die Zeilen und Spalten der Daten zum Sterbefall und klicken Sie auf Einfügen | Diagramme | Liniendiagramm.
- Median-Politur-Analyse als zweite Phase
- Subtrahieren Sie iterativ den Median von jeder Zeile und jeder Spalte, um den kumulativen Effekt von Alter und Zeitraum zu eliminieren. Bewahren Sie nach der medianen Polierphase die Residuen für das Regressionsverfahren auf, um die Kohorteneffekte zu bewerten.
- Berechnen Sie den Gesamtmedian und die Residuestabelle. Importieren Sie eine CSV-Datei mit Sterbedaten der Kontingenztabelle (siehe 2.1.1.2).
- LN wurde für jede Zelle der Kontingenztabelle verwendet: Sterbedaten. Klicken Sie auf Formeln | Mathematische & Trigonometrie-Funktion und wählen Sie LN.
- Zahl: Geben Sie die Standortbeschriftung für jede Zelle ein. Stellen Sie sicher, dass für jede Zelle der Kontingenztabelle die Sterbedaten der LN übernommen wurden. Klicken Sie auf Formeln | Weitere Funktionen | Statistik und wählen Sie MEDIAN aus.
- Zahl1: Geben Sie die erste Beschriftung der Zellenposition ein.
- Zahl2: Geben Sie die Beschriftung der letzten Zellenposition ein. Stellen Sie sicher, dass der resultierende Medianwert am oberen linken Rand der Kontingenztabelle gespeichert wird. Stellen Sie sicher, dass eine Residuentabelle erstellt wird, indem Sie die Differenz zwischen dem ursprünglichen Wert (d. h. den LN-Mortalitätsdaten) und dem Gesamtmedian verwenden.
- Berechnen Sie die Zeilenmediane (d. h. die Mediane jeder Altersgruppe), und stellen Sie sicher, dass die Zeilenmedianwerte für die Antwortaltersgruppe berechnet wurden. Klicken Sie auf Formeln | Weitere Funktionen | Statistik | Wählen Sie MEDIAN aus.
- Nummer 1: Geben Sie die erste Beschriftung der Zelle der Rohprobe ein.
- Nummer 2: Geben Sie die Beschriftung der letzten Zelle des Rohmaterials ein. Stellen Sie sicher, dass die resultierenden Zeilenmedianwerte am linken Rand der Kontingenztabelle gespeichert werden.
- Erstellen Sie eine neue Residuentabelle, nachdem Sie von den Zeilenmedianen subtrahiert haben. Stellen Sie sicher, dass ein neuer Satz von Restwerten aus den Zeilenmedianen erstellt wird, wobei jede Zelle den Wert der Subtraktion des Zeilenmedians von jeder Antwortvariablen in dieser Zeile annimmt. Klicken Sie auf =, und stellen Sie sicher, dass die Beschriftung der gesamten Zellenposition jeder Zeile die Beschriftung des Medians am linken Rand subtrahiert hat.
- Berechnen Sie die Spaltenmediane (d. h. die Mediane jeder Periodengruppe) und stellen Sie sicher, dass die Spaltenmedianwerte für die Antwortperiodengruppe berechnet werden. Klicken Sie auf Formeln | Weitere Funktionen | Statistik | Wählen Sie MEDIAN aus.
- Nummer 1: Geben Sie die Beschriftung der ersten Zellenposition der Spalte ein. Nummer 2: Geben Sie die Beschriftung der letzten Zellenposition der Spalte ein. Stellen Sie sicher, dass die resultierenden Spaltenmedianwerte am oberen Rand der Kontingenztabelle gespeichert werden.
- Erstellen Sie eine neue Residuentabelle, nachdem Sie von den Spaltenmedianen subtrahiert haben. Stellen Sie sicher, dass ein neuer Satz von Restwerten aus den Spaltenmedianen erstellt wird, wobei jede Zelle den Wert der Subtraktion des Spaltenmedians von jeder Antwortvariablen in dieser Spalte annimmt. Klicken Sie auf = und stellen Sie sicher, dass die Beschriftung der gesamten Zellenposition jeder Spalte die Beschriftung des oberen Randmedians subtrahiert hat.
- Wiederholen Sie die Schritte 2.1.2.7 bis 2.1.2.10, bis die Mediane der Zeilen und Spalten ungefähr Null betragen. Klicken Sie auf Formeln | Weitere Funktionen | Statistik | Wählen Sie MEDIAN aus. Stellen Sie sicher, dass der Zeilen- und Spaltenmedian ungefähr Null ist. Speichern Sie die endgültige Residuentabelle im CSV-Format.
- Regressionsverfahren mit Gewichtung als dritte Phase
HINWEIS: Wir haben die abhängige Variable als Residuen für jede Kohorte berechnet, wobei die Sterbezahl die Gewichtung ist. Als nächstes führten wir lineare Regressionen durch, um die Kohorteneffekte zu berechnen.- Stellen Sie sicher, dass Kutools für Excel installiert wurde, und verwenden Sie das Werkzeug Tabellenabmessungen transponieren, um Kreuztabellen schnell in flache Listen umzuwandeln. Importieren Sie eine CSV-Datei mit den Restdaten der Kontingenztabelle (siehe 2.1.2.11).
- Wählen Sie die Tabelle aus, die in eine Liste konvertiert werden soll. Klicken Sie auf die Kutools | Ändern | Tabellendimension transponieren. Vergewissern Sie sich, dass im Dialogfeld Tabellenabmessungen transponieren das Kontrollkästchen neben der Liste Kreuztabelle zu aktivieren ist, und wählen Sie den Ergebnisbereich aus, um die Residuen im Listenformat zu speichern.
- Einfügen einer Spalte in die ursprüngliche Datendatei (siehe 1.2) mit den Daten im Restlistenformat (siehe 2.1.3.1). Stellen Sie sicher, dass eine unterstützende Spalte in die Daten des Restlistenformats eingefügt wurde (siehe 2.1.3.1). Klicken Sie auf = Alters- und Periodenvariablen und klicken Sie auf Enter. Verwenden Sie eine unterstützende Spalte, um die Alters- und Periodengruppenbeschriftungen der Residuenlistenformatdaten nachzuschlagen, um eine Antwortrestspalte in die ursprüngliche Datendatei einzufügen (siehe 1.2).
- Klicken Sie auf Formeln | Nachschlagen & Nachschlagen | Wählen Sie SVERWEIS aus. Legen Sie SVERWEIS fest (Zellenpositionsbeschriftung des Alters und Zellenpositionsbeschriftung des Zeitraums, erste Zellenpositionsbeschriftung der unterstützenden Spalte: die letzte Zellenpositionsbeschriftung der Restspalte, 4, 0). Stellen Sie sicher, dass der Auswahlbereich die Spalten Stütze, Alter, Zeitraum und Rest enthält (d. h. die 4. Spalte als Restliste).
- Stellen Sie sicher, dass die Residuen in die ursprüngliche Datendatei eingefügt werden (siehe 1.2) und suchen Sie für den nächsten Schritt nach den Daten im Restlistenformat (siehe 2.1.3.1). Passen Sie das Regressionsmodell an ungewichtete kleinste Quadrate an, und analysieren Sie die Residuen.
- Klicken Sie auf Analysieren | Regression | Linear. Übertragen Sie die unabhängige Variable, Kohortenkategorie (d. h. 17 Geburtskohorten), in das Feld Unabhängig(e), und die abhängige Variable, Residuen, in das Feld Abhängig:. Klicken Sie auf OK. Stellen Sie sicher, dass die Ergebnisse der ungewichteten Kohorteneffekte generiert werden.
- Stellen Sie sicher, dass die Residuen in die anfängliche Excel-Datendatei eingefügt wurden (siehe 1.2) und suchen Sie für den nächsten Schritt nach den Daten des Restlistenformats (siehe 2.1.3.1). Passen Sie das Regressionsmodell nach gewichteten kleinsten Quadraten an, und analysieren Sie die Residuen. Klicken Sie auf Analysieren | Regression | Linear.
- Übertragen Sie die unabhängige Variable und die Kohortenkategorie (d. h. 17 Geburtskohorten) in das Feld unabhängige(n) Feld und die abhängige Variable und die Residuen in das Feld Abhängige:. Übertragen Sie die Sterbenummer in die WLS-Gewichtsbox. Klicken Sie auf OK. Stellen Sie sicher, dass die Ergebnisse des gewichteten Durchschnitts des Kohorteneffekts generiert werden.
Ergebnisse
Die Mortalitätsdaten wurden für 10 Fünfjahres-Altersgruppen (40-44, 45-49, 50-54, 55-59, 60-64, 65-69, 70-74, 75-79, 80-84 und 85+) und 8 Fünfjahreszeiträume (1976-1980, 1981-1985, 1986-1990, 1991-1995, 1996-2000, 2001-2005, 2006-2010 und 2011-2015) nachgewiesen. Die Anzahl der Kohortengruppen wurde ausgewählt, indem eine von der Gesamtzahl der Altersgruppen subtrahiert wurde: 10 (Fünfjahresgruppen) + 8 (Fünfjahreszeiträume) -1 = 17 Geburtskohorten, wobei die Geburtskohortengruppen nach mittleren Kohortenjahren als 1891, 1896, 1901, 1906, 1911, 1916, 1921, 1926, 1931, 1936, 1941, 1951, 1961, 1961, 1966 und 1971 bezeichnet wurden. Wir stellen ein Format der Altersgruppenkontingenz von Männern und Frauen mit HCC zur Verfügung (in der ergänzenden Tabelle 1). Abbildung 1 und Abbildung 2 zeigen die HCC-Mortalitätsraten innerhalb der Alters- und Periodengruppen. Diese Schwankungen waren bei Männern stärker ausgeprägt als bei Frauen. Das Verhältnis auf Basis der Altersverteilung zeigt, dass am unteren Ende der Altersgruppe der 40- bis 44-Jährigen die HCC-Mortalitätsraten steigen (Abbildung 1). Im Gegensatz dazu zeigt Abbildung 2 deutlich, dass die HCC-Mortalitätsraten in der Altersgruppe der ≥60-Jährigen allmählich anstiegen. Die altersabhängigen HCC-Sterblichkeitsraten haben sich jedoch im Laufe der Zeit erheblich verändert, was bedeutet, dass ein bemerkenswerter Kohorteneffekt, der in der normalen Altersperioden-Kreuzklassifikationstabelle der Vitalstatistik verborgen ist, erst irgendwann in der Zukunft sichtbar wird.
Wir führten das mediane Polierverfahren für logarithmisch-transformierte HCC-Mortalitätsraten ein. Die geschätzten Kohorteneffekte für das APC-Modell der HCC-Mortalitätsraten für Männer und Frauen sind in den Tabellen 1 bzw. 2 dargestellt. Darüber hinaus ist die Berechnung der beiden geschlechtsgewichteten Durchschnittsverfahren vor Erhalt der gewichteten Schätzungen in den Tabellen 1 und 2 aufgeführt. Die gewichteten Schätzungen stimmen besser mit den Daten überein als die zuvor geschätzten Kohorteneffekte, basierend auf der minimalen Abweichung (beim Vergleich gleichgewichteter Schätzungen) des Konfidenzintervalls (KI) der gewichteten Schätzungen.
Für Männer zeigt das linke Feld von Tabelle 1 die Kohorteneffekte der Geburtskohorten. Der Kohorteneffekt steigt von 0,73 (der früheste Kohorteneffekt im Jahr 1891) auf 1,20 (der größte Kohorteneffekt im Jahr 1936). Bei Frauen steigt der Kohorteneffekt von 0,68 (der früheste Kohorteneffekt im Jahr 1891) auf 1,35 (der größte Kohorteneffekt im Jahr 1936). Es ist wichtig zu betonen, dass der Kohorteneffekt für Männer und Frauen im Vergleich zur Kohorte von 1891 um etwa 64 % bzw. 98 % zunahm. Der Anstieg war im rechten Feld von Tabelle 2 gleichmäßig verteilt. Hier stieg der Kohorteneffekt von 0,71 (der früheste Kohorteneffekt im Jahr 1891) auf 1,11 (der größte Kohorteneffekt im Jahr 1936). Für Frauen ist ein ähnlicher Effekt der erhöhten Verteilung in der rechten Spalte von Tabelle 2 zu sehen. Der Kohorteneffekt stieg von 0,64 (der früheste Kohorteneffekt im Jahr 1891) auf 1,11 (der größte Kohorteneffekt im Jahr 1926). Daher beobachteten wir im Vergleich zur frühesten Kohorte von Männern und Frauen einen Anstieg der Sterblichkeitsraten um etwa 57% bzw. 73%.
Unter den Geburtskohorten wiesen Männer, die etwa 1936 geboren wurden, das höchste Risiko für HCC-Mortalität auf (Ergänzende Tabelle 1). Für die gewichteten Schätzungen betrug daher der Einfluss der Geburtskohorte im Jahr 1936 im Vergleich zur Referenzgeburtskohorte von 1921 1,11 (95%-KI: 1,08-1,14). Im Gegensatz dazu zeigte die frühere Kohorte von 1891 einen stark steigenden Trend. Darüber hinaus kehrten sich die Effekte nach der Kohorte von 1936 um. In Tabelle 1 betrug der gewichtete Effekt im Vergleich zur Referenzgeburtenkohorte von 1916 1,11 (95%-KI: 1,07-1,16). Darüber hinaus modellierten wir mit Männern und Frauen gleichgewichtete bzw. gewichtete Kohorteneffekte mit 95%-Konfidenzintervallen. Beide Abbildungen zeigen, dass die gleichgewichteten Kohorteneffekte breiter sind als fast alle Breiten der 95%-KIs.
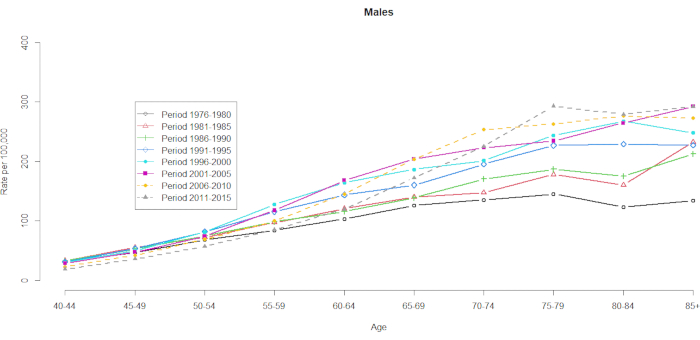
Abbildung 1. HCC-Mortalitätsraten pro 100.000 nach Alter und Zeitraum, Männer, Taiwan, 1976-2015. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.
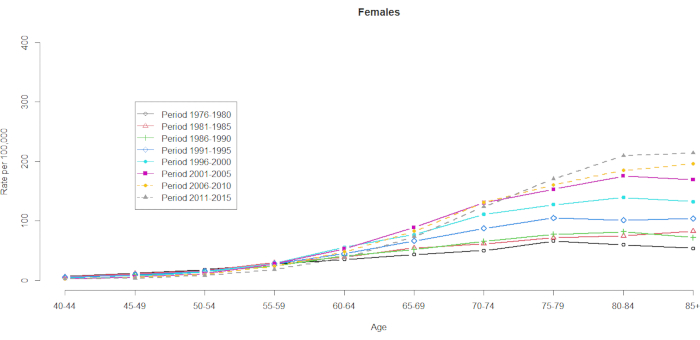
Abbildung 2. HCC-Mortalitätsraten pro 100.000 nach Alter und Zeitraum, Frauen, Taiwan, 1976-2015. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.
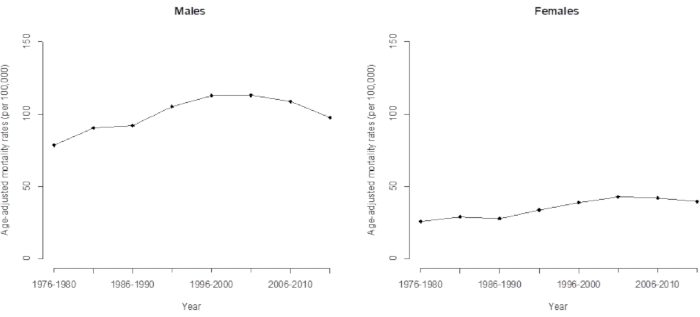
Abbildung 3. Altersbereinigte Mortalitätsrate durch hepatozelluläres Karzinom bei Männern und Frauen in Taiwan. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.
| Unbewertet | Gewichtet | |||
| Effekte | 95 % KI für Effekte | Effekte | 95 % KI für Effekte | |
| Kohorte | ||||
| (1891~1971) | ||||
| 1891 | 0.73 | 0.59-0.90 | 0.71 | 0.57- 0.88 |
| 1896 | 0.88 | 0.79-0.99 | 0.87 | 0.78- 0.97 |
| 1901 | 0.89 | 0.83-0.96 | 0.81 | 0.71- 0.92 |
| 1906 | 0.91 | 0.86- 0.97 | 0.85 | 0.78- 0.94 |
| 1911 | 0.95 | 0.90-1.00 | 0.89 | 0.83- 0.96 |
| 1916 | 1.01 | 0.97-1.06 | 0.99 | 0.95- 1.03 |
| 1921 | 1 | SCHIRI | 1 | SCHIRI |
| 1926 | 1.04 | 1.00-1.08 | 1.03 | 1.01- 1.06 |
| 1931 | 1.1 | 1.06-1.14 | 1.08 | 1.06- 1.11 |
| 1936 | 1.2 | 1.15- 1.24 | 1.11 | 1.08- 1.14 |
| 1941 | 1.14 | 1.09- 1.19 | 1.1 | 1.07- 1.13 |
| 1946 | 1.04 | 1.00-1.09 | 1.06 | 1.04- 1.09 |
| 1951 | 0.91 | 0.87-0.96 | 1 | 0.98- 1.03 |
| 1956 | 0.87 | 0.82-0.92 | 0.96 | 0.93- 0.98 |
| 1961 | 0.82 | 0.76-0.88 | 0.88 | 0.85- 0.92 |
| 1966 | 0.76 | 0.68- 0.85 | 0.79 | 0.74- 0.83 |
| 1971 | 0.71 | 0.57-0.87 | 0.83 | 0.80- 0.87 |
| Hinweis: REF = Referenz; KI = Konfidenzintervall. | ||||
Tabelle 1. Geschätzte Ratenverhältnisse und 95%-Konferenzintervalle für die Wirkung der Geburtskohorte auf die Mortalität des hepatozellulären Karzinoms bei Männern in Taiwan, 1891-1971.
| Unbewertet | Gewichtet | |||
| Effekte | 95 % KI für Effekte | Effekte | 95 % KI für Effekte | |
| Kohorte | ||||
| (1891~1971) | ||||
| 1891 | 0.68 | 0.42- 1.10 | 0.64 | 0.38-1.09 |
| 1896 | 0.81 | 0.63-1.04 | 0.75 | 0.56- 1.00 |
| 1901 | 0.8 | 0.67- 0.95 | 0.7 | 0.52- 0.94 |
| 1906 | 0.83 | 0.72- 0.95 | 0.76 | 0.65- 0.88 |
| 1911 | 0.88 | 0.78- 0.99 | 0.85 | 0.78- 0.93 |
| 1916 | 1 | SCHIRI | 1 | SCHIRI |
| 1921 | 1.12 | 1.01-1.24 | 1.08 | 1.03- 1.13 |
| 1926 | 1.29 | 1.17-1.42 | 1.11 | 1.07- 1.12 |
| 1931 | 1.3 | 1.18-1.43 | 1.1 | 1.05- 1.15 |
| 1936 | 1.35 | 1.22-1.49 | 1.1 | 1.04- 1.14 |
| 1941 | 1.19 | 1.07-1.32 | 1.09 | 1.03-1.13 |
| 1946 | 1.05 | 0.94-1.17 | 1.06 | 1.02-1.11 |
| 1951 | 0.83 | 0.73-0.94 | 1 | 0.96-1.05 |
| 1956 | 0.67 | 0.58-0.77 | 0.93 | 0.89-0.98 |
| 1961 | 0.58 | 0.49-0.70 | 0.79 | 0.74-0.84 |
| 1966 | 0.59 | 0.46-0.75 | 0.58 | 0.49-0.69 |
| 1971 | 0.63 | 0.40-1.02 | 0.64 | 0.58-0.72 |
| Hinweis: REF = Referenz; KI = Konfidenzintervall. | ||||
Tabelle 2. Geschätzte Ratenverhältnisse und 95%-Konferenzintervalle für die Wirkung der Geburtskohorte auf die Mortalität des hepatozellulären Karzinoms bei Frauen in Taiwan, 1891-1971.
Ergänzende Tabelle 1. Bitte klicken Sie hier, um diese Tabelle herunterzuladen.
Diskussion
Aufgrund des Zeittrends der HCC-Mortalität unterschätzen konventionelle Modelle einige wichtige Merkmale, die in den Daten verborgen sind (z. B. Kohorteneffekte), und konventionelle Analysen, die eine einfache lineare Extrapolation der beobachteten logarithmischen Alterskorrekturrate verwenden, zeigen eine signifikant geringere Genauigkeit in ihren Vorhersagen. Es wird deutlich, dass sich dieser Trend seit 35 Jahren fortsetzt und in den nächsten Jahren weiter nach oben tendieren wird, wenn wir den langfristigen Trend der HCC-Mortalität in Taiwan von 1976 bis 2015 direkt beobachten (Abbildung 3). In der Tat ist der jüngste Trend der HCC-Mortalität in Taiwan rückläufig und wird durch den Kohorteneffekt (bestimmt durch die APC-Analyse) angetrieben, der, wie bereits erwähnt, nach der Kohorte von 1936 zurückging. Diese Studie zeigt, dass die Anwendung des APC-Modells erweiterte und genauere Warnungen vor Trendänderungen liefert.
Aus klinischer Sicht gibt es etwa zwei Milliarden Menschen, die mit dem Hepatitis-B-Virus (HBV) 12 infiziert sind, und etwa 350 Millionen Menschen leiden darunter. Folglich handelt es sich um ein bedeutendes Gesundheitsproblem mit weltweit hoher Morbidität. Eine HBV-Infektion verursacht eine Vielzahl klinischer Probleme, einschließlich eines ineffektiven Trägerstatus zur Auslösung von Hepatitis, Zirrhose oder hepatozellulärem Karzinom. Die wirksamste Präventionsmethode besteht darin, Personen mit dem Hepatitis-B-Impfstoff zu impfen. Taiwan führte 1984 den ersten globalen Hepatitis-B-Massenimpfplan ein 13. In diesem Programm wurden schwangere Frauen auf Hepatitis-B-Oberflächenantigen (HBsAg) und Hepatitis-B-Hüllantigen (HBeAg) untersucht 14. In den ersten zwei Jahren dieses Programms umfasste das Impfprogramm nur Babys von Müttern mit HBsAg. Ab dem dritten Jahr des Impfprogramms waren jedoch alle Babys versichert. Die Durchimpfungsrate des Hepatitis-B-Impfstoffs hat in den letzten Jahren 99 % erreicht 15. Fast 90 bis 95 % der Menschen werden nach Erhalt der drei Dosen des Impfstoffs eine lebenslange Immunität erfahren. Wir betonen, dass der Rückgang des pädiatrischen HCC in Taiwan weitgehend auf dieses globale Impfprogramm zurückzuführen ist.
Die in diesem Artikel dargestellte APC-Modellierung bietet eine Vorwarnung vor diesen (verstärkten) Trendänderungen (die in naher Zukunft abnehmen werden). Beim Vergleich des Trends der Kohorteneffekte (Tabellen 1 und 2) und der altersbereinigten Mortalität (Abbildung 3) entsprach die direkte altersbereinigte Mortalitätsrate (oder altersstandardisierte Mortalitätsrate) dem gewichteten Durchschnitt. Sie gewichtet die Alterssterblichkeitsraten nach dem Anteil der interessierenden Altersgruppe, basierend auf der World Standard Population 16 aus dem Jahr 2000 in dieser Studie. Da die Validierung von Kohorteneffekten das neueste Muster der HCC-Mortalität dominierte, berechneten wir die altersbereinigte HCC-Mortalität für die aktuellen Daten (bis 2011-2015). Wir interpretierten dies so, dass die gewichtete mittlere Schätzung der Kohorten zuverlässige Informationen liefert, während die Forschung darauf vorbereitet ist, die zukünftige HCC-Mortalität vorherzusagen. Details zur Vorhersage der HCC-Mortalität finden Sie in unserer vorherigen Studie 5.
Eine allgemeine Hypothese ist, dass jeder Wert in den Daten die gleichen Informationen liefert, um die Parameter in einem Modell auszuwerten. Dieser Ansatz wurde in den meisten Modellierungsmethoden (z. B. linearen oder nichtlinearen Regressionsmodellen) verwendet und bedeutet, dass die Standardabweichung des Fehlerterms die konstante zugrunde liegende Prädiktorvariable ist. Nach unserer Literaturrecherche ist diese Hypothese jedoch nicht für die Modellierung zur empirischen Abschätzung von Parametern geeignet. Die unbekannten Parameter werden geschätzt, wenn wir die gewichtete Regression verwenden, die eine kleinere Gewichtung mit geringerer Genauigkeit für Datenpunkte und eine große Gewichtung mit höherer Genauigkeit für Datenpunkte generiert. Durch den Gewichtungsprozess wurde die Standardabweichung des Schätzers verringert. Dennoch sind die Unzulänglichkeiten der gewichteten Regressionsmethode in der empirischen Praxis nahezu unbekannt. Da die genauen Gewichte nicht bekannt sind, wurden die geschätzten Gewichte zur Schätzung der Parameter verwendet. Darüber hinaus haben frühere Erfahrungen gezeigt, dass sich die auf Schätzungen basierende Gewichtung nicht wesentlich ändert oder die Regressionsanalyse oder deren Interpretation in der Regel beeinflusst 17. Hypothetisch kann das APC-Modell an jede Krankheit angepasst werden, bei der die Inzidenz durch Alter, Zeitraum und Kohorte beeinflusst wird. Darüber hinaus wurden gewichtete mittlere Schätzungen für die Vorhersage 18,19,20 zur Verfügung gestellt. Ist das KI vergleichsweise eng, ist die Unsicherheit gering. In Anbetracht der Tatsache, dass das CI die Unsicherheit abbildet, die dieser Art der Bewertung innewohnt, und die darin enthaltenen Werte, kommen wir im Allgemeinen zu dem Schluss, dass die Verwendung von CI einen erheblichen Einfluss hat.
Die transkatheterarterielle Chemoembolisation (TACE) ist eine der effizientesten Methoden zur klinischen Kontrolle des HCC. Es ist jedoch schwierig, diese Methode als Haupt- oder Hilfstherapie zu wählen, da keine offene Operation erforderlich ist. Die Leber liefert in der Regel 75 % des Blutes und der Nährstoffe über die Leberpfortader, während die Leberarterie 25 % des Blutes und der Nährstoffe liefert. Im Gegensatz zum Leberarterienblut, das aus den meisten HCCs entnommen wird, nimmt diese Flüssigkeit schnell zu und kommt selten aus der Leberpfortader. Darüber hinaus ist dieser Effekt gut für TACE geeignet, da primärer Leberkrebs selten in andere Teile des Körpers metastasiert. Auch wenn es unwahrscheinlich ist, dass hepatozelluläre bösartige Tumoren Metastasen bilden, sind sie schwer auszurotten. In der klinischen Praxis wird die Nachsorge für HCC-Patienten alle zwei bis drei Monate durchgeführt. Sobald eine abnormale Erhöhung des Alpha-Fetoproteins (AFP) oder eine abnormale Ultraschalluntersuchung festgestellt wird, werden Computertomographie und Magnetresonanztomographie durchgeführt. Wenn ein neuer Tumor entdeckt wird, wird TACE in Betracht gezogen. Es wurden auch neue Biomarker entwickelt, um das Wiederauftreten von HBV-bedingtem HCC nachzuweisen, wie z. B. der quantitative Zeitindex der HBV-DNA (HDQTI) 21. Das Produkt aus den Follow-up-Ergebnissen und dem Logarithmus des Verhältnisses von nachgewiesener zu normaler HBV-DNA-Last ist die Summe der HDQTIs. Der HDQTI wird als unabhängiger prognostischer Indikator für das HBV-bedingte HCC-Rezidiv verwendet 21.
Unsere Studie hat mehrere Einschränkungen. Zunächst stellten wir lediglich Hypothesen über die Ätiologien der beobachteten Veränderungen auf. Unter Verwendung des APC-Modells wurde die HCC-Mortalität nach Alter, Zeitraum und Kohorteneffekten neu betrachtet. Nichtsdestotrotz haben wir in dieser Studie die mittlere Poliereinstellung als Annahme verwendet. Zweitens wird die APC-Analyse im Bereich der Epidemiologie in Entwicklungsländern oder kürzlich entwickelten Ländern für Langzeitkohortenstudien häufig eingesetzt. Drittens hatten wir keine Informationen aus dem akkumulierten Format-Datensatz, um Störfaktoren im APC-Modell, wie z. B. Komorbiditäten oder Lebensstil, zu berücksichtigen. Isolierte Daten werden für zukünftige Forschungen benötigt, um diese Einschränkung zu beheben. Viertens haben wir, um das Regressionsverfahren in der mehrstufigen Methode zu modifizieren, die Anzahl der Todesfälle aufgrund von HCC als Gewichtung verwendet. Da das genaue Gewicht nicht bekannt ist, führt die Verwendung verschiedener Gewichte zu einer leichten Inflation innerhalb der geschätzten Kohorteneffekte. Letztendlich gibt es verschiedene APC-Schätzmethoden, um das nicht erkennbare Problem zu lösen (z. B. verwendet Holford lineare und Krümmungstrends, um das nicht erkennbare Problem 22 zu lösen). Gleichzeitig liefert der Median Polish komplexe Annahmen in Form von konzeptioneller Konversion zwischen APC-Modellen, um den Kohorteneffekt mit den wenigsten Annahmen zu bewerten, und wendet problemlos ein gemeinsames Format für Kontingenztabellen an.
Insgesamt wurde dann der gewichtete mittlere Effekt mit einem vergleichsweise engen KI jeder Kohorte durch die gewichtete Schätzung zur Modifikation des Regressionsmodells zugelassen. Kurz gesagt, für mehrstufige Methoden ist es ratsam, gewichtete Schätzungen von Regressionsmodellen zu verwenden, um die Kohorteneffekte in den Daten der Altersperioden-Kontingenztabelle zu bewerten.
Offenlegungen
Die Autoren haben nichts offenzulegen.
Danksagungen
Diese Arbeit wurde unterstützt durch das Taipei Tzu Chi Hospital TCRD-TPE-109-RT-8 (2/3) und TCRD-TPE-109-39 (2/2).
Materialien
| Name | Company | Catalog Number | Comments |
| not applicable | not applicable | not applicable | not applicable |
Referenzen
- Kuntz, E., Kuntz, H. D. . Hepatology: Principles and Practice. , 774 (2006).
- McGlynn, K. A., et al. International trends and patterns of primary liver cancer. International Journal of Cancer. 94 (2), 290-296 (2001).
- Bosch, F. X., Ribes, J., Diaz, M., Cleries, R. Primary liver cancer: worldwide incidence and trends. Gastroenterology. 127, 5-16 (2004).
- Tzeng, I. S., Ng, C. Y., Chen, J. Y., Chen, L. S., Wu, C. C. Using weighted regression model for estimating cohort effect in age-period contingency table data. Oncotarget. 9 (28), 19826-19835 (2018).
- Tzeng, I. S., Lee, W. C. Forecasting hepatocellular carcinoma mortality in Taiwan using an age-period-cohort model. Asia-Pacific Journal of PublicHealth. 27, 65-73 (2015).
- Tzeng, I. S., et al. Predicting emergency departments visit rates from septicemia in Taiwan using an age-period-cohort model, 1998 to 2012. Medicine. 95, 5598 (2016).
- Chen, S. H., et al. Period and Cohort Analysis of Rates of Emergency Department Visits Due to Pneumonia in Taiwan, 1998-2012. Risk Management and Healthcare Policy. 13, 1459-1466 (2020).
- Keyes, K. M., Li, G. A multiphase method for estimating cohort effects in age-period contingency table data. Annals of Epidemiology. 20, 779-785 (2010).
- Tukey, J. . Exploratory data analysis Reading: MS. , (1977).
- Selvin, S. . Statistical analysis of epidemiologic data. , (1996).
- Légaré, G., Hamel, D. An age-period-cohort approach to analyzing trends in suicide in Quebec between 1950 and 2009. Canadian Journal of Public Health. 104, 118-123 (2013).
- Lavanchy, D. Hepatitis B virus epidemiology, disease burden, treatment, and current and emerging prevention and control measures. Journal of Viral Hepatitis. 11, 97-107 (2004).
- Chang, M. H., et al. Universal hepatitis B vaccination in Taiwan and the incidence of hepatocellular carcinoma in children. Taiwan Childhood Hepatoma Study Group. New England Journal of Medicine. 336, 1855-1859 (1997).
- Lu, F. T., Ni, Y. H. Elimination of mother-to-infant transmission of hepatitis B virus: 35 years of experience. Pediatric Gastroenterology, Hepatology & Nutrition. 23 (4), 311-318 (2020).
- Chien, Y. C., Jan, C. F., Kuo, H. S., Chen, C. J. Nationwide hepatitis B vaccination program in Taiwan: effectiveness in the 20 years after it was launched. Epidemiologic Reviews. 28, 126-135 (2006).
- Ahmad, O. B., et al. Age standardization of rates: a new WHO standard. Geneva: GPE Discussion Paper Series. World Health Organization. , 31 (2005).
- da Silva, C. P., Emídio, E. S., de Marchi, M. R. Method validation using weighted linear regression models for quantification of UV filters in water samples. Talanta. 131, 221-227 (2015).
- Dawes, R. M. The robust beauty of improper linear models in decision making. American Psychologist. 34, 571-582 (1979).
- Dawes, R. M., Corrigan, B. Linear models in decision making. Psychological Bulletin. 81, 95-106 (1974).
- Einhorn, H. J., Hogarth, R. M. Unit weighting schemes for decision making. Organizational Behavior and Human Performance. 13, 171-192 (1975).
- Wang, W., et al. Association of hepatitis B virus DNA level and follow-up interval with hepatocellular carcinoma recurrence. JAMA Network Open. 3 (4), 203707 (2020).
- Holford, T. R. The estimation of age, period and cohort effects for vital rates. Biometrics. 39, 311-324 (1983).
Nachdrucke und Genehmigungen
Genehmigung beantragen, um den Text oder die Abbildungen dieses JoVE-Artikels zu verwenden
Genehmigung beantragenThis article has been published
Video Coming Soon
Copyright © 2025 MyJoVE Corporation. Alle Rechte vorbehalten