Method Article
Pronóstico de la mortalidad por carcinoma hepatocelular mediante un modelo de regresión ponderada para estimar los efectos de cohorte en Taiwán
En este artículo
Resumen
Describimos un método multietápico para medir un efecto de cohorte con datos de edad, lo que permite eliminar los datos en muchas situaciones sin sacrificar la calidad de los datos. El protocolo demuestra la estrategia y proporciona un modelo de regresión ponderada para analizar los datos del carcinoma hepatocelular.
Resumen
Para eliminar la influencia de la edad y el período en los datos de la tabla de contingencia del ciclo de edad, se adoptó un método polietápico para evaluar el efecto de cohorte. El tumor maligno primario más general del hígado es el carcinoma hepatocelular (CHC). El CHC se asocia con cirrosis hepática con alcohol y etiologías virales. En epidemiología, se delinearon (o pronosticaron) las tendencias a largo plazo de la mortalidad por CHC mediante un modelo de cohorte por edad (APC). Las muertes por CHC se determinaron para cada cohorte con su influencia ponderada. El intervalo de confianza (IC) de la media ponderada es bastante estrecho (en comparación con las estimaciones igualmente ponderadas). Debido al IC bastante estrecho y con menor incertidumbre, se utilizó la estimación de la media ponderada como medio para la predicción. Con el método polietápico, se recomienda utilizar una estimación de la media ponderada basada en un modelo de regresión para evaluar el efecto de la cohorte en los datos de la tabla de contingencia por edad-período.
Introducción
El tumor maligno primario más común del hígado es el carcinoma hepatocelular (CHC). Su tasa de mortalidad ocupa el quinto lugar en los hombres y el octavo en las mujeres (6% de los hombres y 3% de las mujeres) 1 entre todos los tumores malignos del mundo. En Taiwán, es el cáncer más común en los hombres y el segundo cáncer más común en las mujeres (21,8% de los hombres y 14,2% de las mujeres) 2. Se estima que desde el año 2000, el número anual de CHC diagnosticados en todo el mundo es de 564.000, de los cuales 398.000 son hombres y 166.000 son mujeres 3. En epidemiología, la forma más común de explicar la relación entre las variables edad, período y cohorte (APC) es que la edad y el período se influyen mutuamente para crear una experiencia generacional única para la tendencia de la enfermedad investigada.
A pesar de que esta conceptualización todavía tiene una conexión lineal precisa de edad + cohorte = período, la exposición (predictor) no es un factor inherente en una cohorte de nacimiento. En cambio, proponemos que cuando los cambios causan diferentes distribuciones de la enfermedad, hay un efecto de cohorte. Sin embargo, dado que edad + cohorte = período, estas tres variables están relacionadas linealmente; solo si se aplican otras restricciones es imposible generar un modelo de cohorte de edad-período (APC) estimado utilizando los efectos lineales de la edad, el período y la cohorte. En este estudio, esclarecimos esta problemática y las posibles restricciones que impusimos en nuestras publicaciones anteriores 4,5,6,7.
Con las más mínimas conjeturas sobre los datos de la tabla de contingencia, el método multietápico 8 proporciona tres etapas para evaluar el efecto de cohorte. Además, dado que el pulido de la mediana no depende de una distribución o marco específico, se utilizó para varios tipos de datos, como proporciones, razones logarítmicas y recuentos. El pulido mediano es la técnica principal utilizada en el método multifásico.
Se utilizaron los datos de una tabla de contingencia bidireccional 9 para generar el desarrollo de la mediana pulida. El procedimiento de pulido de la mediana se utiliza para eliminar los efectos acumulativos de la edad (es decir, la fila) y el período (es decir, la columna) restando iterativamente la mediana de cada fila y cada columna. Este procedimiento es frecuentemente utilizado en el análisis de datos epidemiológicos 10. Una ventaja de esta técnica es que no se requieren suposiciones sobre la distribución o estructura de los datos en la tabla de contingencia bidireccional. Por lo tanto, esta técnica fue ampliamente utilizada para cualquier tipo de datos contenidos en la tabla, como los datos de suicidio 11. El modelo APC también se ha utilizado para describir las tendencias a largo plazo de la incidencia de enfermedades o la mortalidad 5. Los modelos APC a menudo asumen que la edad, el período y la cohorte tienen efectos aditivos en la transformación logarítmica de la enfermedad y la mortalidad. Para evaluar los efectos de cohorte, el protocolo descrito genera un modelo APC para el análisis de la mortalidad por carcinoma hepatocelular (CHC) completo con regresión ponderada, lo que respalda predicciones confiables y una evaluación moderada de los efectos del tratamiento.
Protocolo
1. Fuentes de datos
Para demostrar los cálculos, utilizamos datos anuales sobre la mortalidad por CHC de 1976 a 2015 para hombres y mujeres en Taiwán. Para la ejecución de los protocolos de este estudio se utilizaron los programas SPSS versión 24.0 para Windows y Microsoft Excel.
- Hacer que el médico del CHC clasifique los síntomas clínicos, las pruebas de laboratorio y los resultados de las imágenes médicas de los pacientes para dar un código de diagnóstico de acuerdo con el Código de la Clasificación Internacional de Enfermedades (CIE), CIE 150.
- Asegúrese de que el archivo de datos (guardado como CSV) contenga el año (es decir, el período), la edad, la cohorte, el número de defunciones, el número de población de mitad de año y la mortalidad como columnas.
- Haga clic en Archivo | Importar datos | Datos CSV | Abierto. Asegúrese de que haya una marca de verificación en la casilla junto a Leer nombres de variables de la primera fila de los datos y haga clic en Aceptar. Asegúrese de que el fichero de datos se ha importado en SPSS.
- Construir datos de tablas de contingencia cruzados por grupos de edad a través de SPSS. En general, definimos las variables de fila como edad y las variables de columna como período. Si los datos presentaban datos de un solo período de año (o de un solo año de edad), era necesario integrarlos en un grupo de período (o grupo de edad). A continuación, hicimos una tabulación cruzada de las actitudes hacia un grupo de edad a lo largo de los años de la encuesta.
- Haga clic en Analizar | Estadística Descriptiva | Tablas de referencias cruzadas y seleccione la variable de edad en el cuadro junto a las filas y la variable de período en el cuadro junto a las columnas. Haga clic en Celdas y asegúrese de que haya una marca de verificación en la casilla junto a Observado. Una tabla de contingencia del número de defunciones (o número de población a mitad de año, o mortalidad) se puede realizar en SPSS mediante los pasos anteriores.
- Exporte los datos de la tabla de contingencia que se ingresaron en formato CSV para su análisis a través de otro software. Haga clic en Archivo | Exportar datos | Asegúrese de que el formato de datos deseado sea CSV | Ubicación. Este campo no editable muestra la ubicación segura del archivo exportado.
- Nombre de archivo: haga clic en Seleccionar para cambiar el nombre del archivo.
- Exportar como tipo: selecciona un tipo de archivo CSV en el menú desplegable. Haga clic en Variables para mostrar las variables disponibles y seleccionar las tablas de variables. De forma predeterminada, todas las variables del conjunto de datos de origen se conservan para el archivo exportado. Los investigadores pueden utilizar las tablas para especificar qué variables de origen incluir en el archivo exportado. Haga clic en Exportar.
2. Configuración del modelo
NOTA: El método multietápico fue propuesto por Keys y Li 8 con investigación gráfica. Se realizó un análisis de la mediana de pulido para eliminar los efectos acumulativos de la edad y el período; Finalmente, se regresión de estos residuos de la fase de pulido mediano en la categoría de cohorte en el modelo de regresión lineal y se evaluaron los efectos de cohorte utilizando los datos de la tabla de contingencia.
- La representación gráfica como primera fase
- Cree un diagrama de líneas de grupos de edad y grupos de período. Para inspeccionar cohortes de nacimiento en todos los grupos de edad o cohortes de nacimiento, dibuje incluso cohortes de nacimiento en todas las edades o ciclos en los gráficos de líneas.
- Importe un archivo CSV con los datos de mortalidad de la tabla de contingencia. Haga clic en Archivo | Abierto | Busque para seleccionar un archivo CSV de una carpeta. Recuerde elegir Todos los archivos en la lista desplegable junto al cuadro Nombre de archivo.
- Haga clic en Abrir para abrir el archivo CSV. Resalte las filas y columnas de los datos de contingencia de mortalidad y haga clic en Insertar | Gráficos | Gráfico de líneas.
- Análisis de la mediana del pulido como segunda fase
- Reste iterativamente la mediana de cada fila y cada columna para eliminar el efecto acumulativo de la edad y el período. Después de la fase de pulido de la mediana, guarde los residuos para el procedimiento de regresión con el fin de evaluar los efectos de la cohorte.
- Calcule la mediana general y la tabla residual. Importe un archivo CSV con los datos de mortalidad de la tabla de contingencia (consulte 2.1.1.2).
- Para cada celda de la tabla de contingencia se utilizó la LN de datos de mortalidad. Haga clic en Fórmulas | Función Matemática y Trigonometría y seleccione LN.
- Número: Introduzca la etiqueta de ubicación de cada celda. Asegúrese de que cada celda de los datos de mortalidad de la tabla de contingencia tomó LN. Haga clic en Fórmulas | Más funciones | Estadísticas y seleccione MEDIANA.
- Número 1: Introduzca la primera etiqueta de ubicación de celda.
- Número 2: Introduzca la etiqueta de ubicación de la última celda. Asegúrese de que el valor mediano resultante se almacene en el margen superior izquierdo de la tabla de contingencia. Asegúrese de crear una tabla de residuos tomando la diferencia entre el valor original (es decir, los datos de mortalidad por LN) y la mediana general.
- Calcule las medianas de las filas (es decir, las medianas de cada grupo de edad) y asegúrese de que calculó los valores de la mediana de las filas para el grupo de edad de la respuesta. Haga clic en Fórmulas | Más funciones | Estadísticas | Seleccione MEDIANA.
- Número 1: Introduzca la primera etiqueta de ubicación de celda de la muestra sin procesar.
- Número 2: Introduzca la última etiqueta de ubicación de celda del material en bruto. Asegúrese de que los valores medianos de fila resultantes se almacenen en el margen izquierdo de la tabla de contingencia.
- Cree una nueva tabla residual después de restar de las medianas de fila. Asegúrese de que se crea un nuevo conjunto de valores residuales a partir de las medianas de fila en el que cada celda toma el valor de la resta de la mediana de fila de cada variable de respuesta de esa fila. Haga clic en = y asegúrese de que la etiqueta de ubicación de celda general de cada fila haya restado la etiqueta de la mediana del margen izquierdo.
- Calcule las medianas de las columnas (es decir, las medianas de cada grupo de períodos) y asegúrese de que calcula los valores de las medianas de las columnas para el grupo de períodos de respuesta. Haga clic en Fórmulas | Más funciones | Estadísticas | Seleccione MEDIANA.
- Número 1: Introduzca la primera etiqueta de ubicación de celda de la columna. Número 2: Introduzca la última etiqueta de ubicación de celda de la columna. Asegúrese de que los valores medianos de columna resultantes se almacenen en el margen superior de la tabla de contingencia.
- Cree una nueva tabla de residuos después de restar de las medianas de las columnas. Asegúrese de que se crea un nuevo conjunto de valores residuales a partir de las medianas de las columnas, donde cada celda toma el valor de la resta de la mediana de la columna de cada variable de respuesta de esa columna. Haga clic en = y asegúrese de que la etiqueta de ubicación general de la celda de cada columna haya restado la etiqueta de la mediana del margen superior.
- Repita los pasos 2.1.2.7 a 2.1.2.10 hasta que las medianas de fila y columna se aproximen a cero. Haga clic en Fórmulas | Más funciones | Estadísticas | Seleccione MEDIANA. Asegúrese de que las medianas de fila y columna sean aproximadamente cero. Guarde la tabla final de residuos en formato CSV.
- Procedimiento de regresión con el peso como tercera fase
NOTA: Calculamos la variable dependiente como residuales para cada cohorte con el número de muertes como peso. A continuación, se realizaron regresiones lineales para calcular los efectos de cohorte.- Asegúrese de que Kutools para Excel se instaló y use su herramienta Transponer dimensiones de tabla para convertir rápidamente tablas cruzadas en listas planas. Importe un archivo CSV con datos residuales de la tabla de contingencia (consulte 2.1.2.11).
- Seleccione la tabla que desea convertir en una lista. Haga clic en el botón Kutools | Modificar | Dimensión de la tabla de transposición. En el cuadro de diálogo Transponer dimensiones de tabla, asegúrese de que haya una marca de verificación en la casilla situada junto a la tabla cruzada a la lista y seleccione el rango de resultados para almacenar los valores residuales en formato de lista.
- Inserto de columna en el archivo de datos inicial (consulte 1.2) con los datos de formato de lista residual (consulte 2.1.3.1). Asegúrese de que ha insertado una columna de apoyo en los datos de formato de lista residual (consulte 2.1.3.1). Haga clic en = variables de edad y período y haga clic en Intro. Utilice una columna de apoyo para buscar las etiquetas de grupo de edad y período de los datos de formato de lista residual para insertar una columna residual de respuesta en el archivo de datos inicial (consulte 1.2).
- Haga clic en Fórmulas | Búsqueda y referencia | Seleccione BUSCARV. Establezca BUSCARV (etiqueta de ubicación de celda de edad y etiqueta de ubicación de celda del período, primera etiqueta de ubicación de celda de la columna de soporte: la última etiqueta de ubicación de celda de la columna residual, 4, 0). Asegúrese de que el rango de selección incluya columnas de soporte, edad, período y residuales (es decir, la4ª columna como la lista de residuales).
- Asegúrese de que los residuos estén insertados en el archivo de datos inicial (consulte 1.2), busque los datos del formato de lista residual (consulte 2.1.3.1) para el siguiente paso. Ajuste el modelo de regresión por mínimos cuadrados no ponderados y analice los residuos.
- Haga clic en Analizar | Regresión | Lineal. Transfiera la variable independiente, categoría de cohorte (es decir, 17 cohortes de nacimiento), al cuadro Independiente(s), y la variable dependiente, Residuales, al cuadro Dependiente:. Haga clic en Aceptar. Asegúrese de generar los resultados de los efectos de cohorte no ponderados.
- Asegúrese de que los residuos estén insertados en el archivo de datos inicial de Excel (consulte 1.2), busque los datos de formato de lista residual (consulte 2.1.3.1) para el siguiente paso. Ajuste el modelo de regresión por mínimos cuadrados ponderados y analice los residuos. Haga clic en Analizar | Regresión | Lineal.
- Transfiera la variable independiente y la categoría de cohorte (es decir, 17 cohortes de nacimiento) a la casilla independiente(s) y la variable dependiente y los residuales a la casilla dependiente:. Transfiera el número de defunción a la caja de peso WLS. Haga clic en Aceptar. Asegúrese de que genera los resultados de la media ponderada del efecto de cohorte.
Resultados
Los datos de mortalidad se demostraron para 10 grupos de edad de cinco años (40-44, 45-49, 50-54, 55-59, 60-64, 65-69, 70-74, 75-79, 80-84 y 85+) y 8 períodos de cinco años (1976-1980, 1981-1985, 1986-1990, 1991-1995, 1996-2000, 2001-2005, 2006-2010 y 2011-2015). El número de grupos de cohorte se seleccionó restando uno del número total de grupos de edad: 10 (grupos de edad de cinco años) + 8 (períodos de tiempo de cinco años) -1 = 17 cohortes de nacimiento, con los grupos de cohortes de nacimiento denotados por años de cohorte intermedia como 1891, 1896, 1901, 1906, 1911, 1916, 1921, 1926, 1931, 1936, 1941, 1946, 1951, 1956, 1961, 1966 y 1971. Proporcionamos un formato de la contingencia del grupo de edad de hombres y mujeres con CHC (en la Tabla Suplementaria 1). En las figuras 1 y 2 se muestran las tasas de mortalidad por CHC en los grupos de edad y período. Estas fluctuaciones fueron más sustanciales entre los hombres que entre las mujeres. La razón basada en la distribución por edad muestra que en el extremo inferior del grupo de 40 a 44 años, las tasas de mortalidad por CHC están aumentando (Figura 1). En contraste, la Figura 2 muestra claramente que las tasas de mortalidad por CHC aumentaron gradualmente en el grupo de edad ≥60 años. Sin embargo, las tasas de mortalidad por CHC basadas en la edad han cambiado sustancialmente con el tiempo, lo que significa que un notable efecto de cohorte oculto en la tabla de estadísticas vitales clasificadas de manera cruzada de período de edad normal no se hará evidente hasta algún momento en el futuro.
Implementamos el procedimiento de pulido de la mediana de las tasas de mortalidad por CHC transformadas logarítmicamente. En los Cuadros 1 y 2, respectivamente, se muestran los efectos estimados de la cohorte para el modelo APC de las tasas de mortalidad por CHC en hombres y mujeres. Además, en los cuadros 1 y 2 se presenta el cálculo de los dos procedimientos de promedio ponderado por género antes de obtener las estimaciones ponderadas. Las estimaciones ponderadas se ajustan mejor a los datos que los efectos de cohorte estimados anteriormente, sobre la base de la desviación mínima (comparando estimaciones igualmente ponderadas) del intervalo de confianza (IC) de las estimaciones ponderadas.
En el caso de los hombres, el panel izquierdo de la Tabla 1 muestra los efectos de las cohortes de nacimiento. El efecto de cohorte aumenta de 0,73 (el primer efecto de cohorte en 1891) a 1,20 (el mayor efecto de cohorte en 1936). En el caso de las mujeres, el efecto de cohorte aumenta de 0,68 (el primer efecto de cohorte en 1891) a 1,35 (el mayor efecto de cohorte en 1936). Es importante destacar que, en comparación con la cohorte de 1891, el efecto cohorte para hombres y mujeres aumentó aproximadamente un 64% y un 98%, respectivamente. El aumento se distribuyó de manera equitativa en el panel derecho de la Tabla 2. Aquí, el efecto de cohorte aumentó de 0,71 (el primer efecto de cohorte en 1891) a 1,11 (el mayor efecto de cohorte en 1936). En el caso de las mujeres, en la columna derecha de la Tabla 2 se muestra un efecto similar de una mayor distribución. El efecto de cohorte aumentó de 0,64 (el primer efecto de cohorte en 1891) a 1,11 (el mayor efecto de cohorte en 1926). Por lo tanto, en comparación con la cohorte más temprana de hombres y mujeres, observamos un aumento en las tasas de mortalidad de aproximadamente 57% y 73%, respectivamente.
Entre las cohortes de nacimiento, los hombres nacidos aproximadamente en 1936 mostraron el riesgo más alto de mortalidad por CHC (Cuadro suplementario 1). Por lo tanto, para las estimaciones ponderadas, el impacto de la cohorte de nacimiento en 1936 en comparación con el de la cohorte de nacimiento de referencia en 1921 fue de 1,11 (IC 95%: 1,08-1,14). En contraste, la cohorte anterior de 1891 mostró una tendencia marcadamente creciente. Además, los efectos se revirtieron después de la cohorte de 1936. En la Tabla 1, en comparación con la cohorte de nacimiento de referencia de 1916, el efecto ponderado fue de 1,11 (IC 95%: 1,07-1,16). Además, con hombres y mujeres, modelamos efectos de cohorte ponderados y ponderados por igual, respectivamente, con intervalos de confianza del 95%. Ambas figuras muestran que los efectos de cohorte ponderados por igual son más amplios que casi todos los anchos de los IC del 95%.
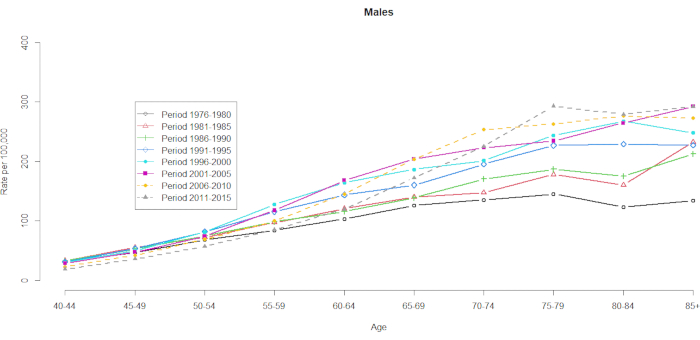
Figura 1. Tasas de mortalidad por 100 000 CHC por edad y período, hombres, Taiwán, 1976-2015. Haga clic aquí para ver una versión más grande de esta figura.
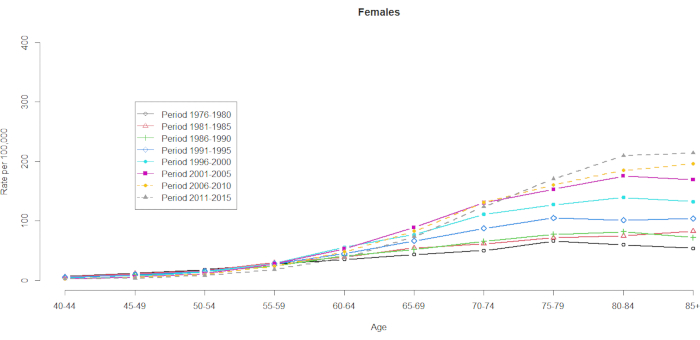
Figura 2. Tasas de mortalidad por 100.000 CHC por edad y período, mujeres, Taiwán, 1976-2015. Haga clic aquí para ver una versión más grande de esta figura.
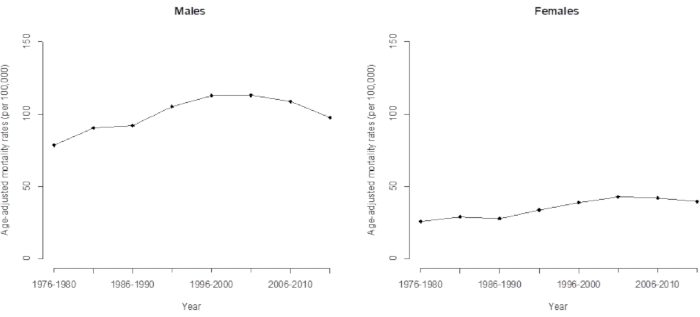
Figura 3. Tasa de mortalidad ajustada por edad por carcinoma hepatocelular en hombres y mujeres en Taiwán. Haga clic aquí para ver una versión más grande de esta figura.
| Sin ponderar | Ponderado | |||
| Efectos | IC del 95% para los efectos | Efectos | IC del 95% para los efectos | |
| Cohorte | ||||
| (1891~1971) | ||||
| 1891 | 0.73 | 0.59-0.90 | 0.71 | 0.57- 0.88 |
| 1896 | 0.88 | 0.79-0.99 | 0.87 | 0.78- 0.97 |
| 1901 | 0.89 | 0.83-0.96 | 0.81 | 0.71- 0.92 |
| 1906 | 0.91 | 0.86- 0.97 | 0.85 | 0.78- 0.94 |
| 1911 | 0.95 | 0.90-1.00 | 0.89 | 0.83- 0.96 |
| 1916 | 1.01 | 0.97-1.06 | 0.99 | 0.95- 1.03 |
| 1921 | 1 | REF | 1 | REF |
| 1926 | 1.04 | 1.00-1.08 | 1.03 | 1.01- 1.06 |
| 1931 | 1.1 | 1.06-1.14 | 1.08 | 1.06- 1.11 |
| 1936 | 1.2 | 1.15- 1.24 | 1.11 | 1.08- 1.14 |
| 1941 | 1.14 | 1.09- 1.19 | 1.1 | 1.07- 1.13 |
| 1946 | 1.04 | 1.00-1.09 | 1.06 | 1.04- 1.09 |
| 1951 | 0.91 | 0.87-0.96 | 1 | 0.98- 1.03 |
| 1956 | 0.87 | 0.82-0.92 | 0.96 | 0.93- 0.98 |
| 1961 | 0.82 | 0.76-0.88 | 0.88 | 0.85- 0.92 |
| 1966 | 0.76 | 0.68- 0.85 | 0.79 | 0.74- 0.83 |
| 1971 | 0.71 | 0.57-0.87 | 0.83 | 0.80- 0.87 |
| Nota: REF = referencia; IC = intervalo de confianza. | ||||
Tabla 1. Índices de tasas estimados e intervalos de conferencia del 95% para el efecto de la cohorte de nacimiento en la mortalidad por carcinoma hepatocelular de hombres en Taiwán, 1891-1971.
| Sin ponderar | Ponderado | |||
| Efectos | IC del 95% para los efectos | Efectos | IC del 95% para los efectos | |
| Cohorte | ||||
| (1891~1971) | ||||
| 1891 | 0.68 | 0.42- 1.10 | 0.64 | 0.38-1.09 |
| 1896 | 0.81 | 0.63-1.04 | 0.75 | 0.56- 1.00 |
| 1901 | 0.8 | 0.67- 0.95 | 0.7 | 0.52- 0.94 |
| 1906 | 0.83 | 0.72- 0.95 | 0.76 | 0.65- 0.88 |
| 1911 | 0.88 | 0.78- 0.99 | 0.85 | 0.78- 0.93 |
| 1916 | 1 | REF | 1 | REF |
| 1921 | 1.12 | 1.01-1.24 | 1.08 | 1.03- 1.13 |
| 1926 | 1.29 | 1.17-1.42 | 1.11 | 1.07- 1.12 |
| 1931 | 1.3 | 1.18-1.43 | 1.1 | 1.05- 1.15 |
| 1936 | 1.35 | 1.22-1.49 | 1.1 | 1.04- 1.14 |
| 1941 | 1.19 | 1.07-1.32 | 1.09 | 1.03-1.13 |
| 1946 | 1.05 | 0.94-1.17 | 1.06 | 1.02-1.11 |
| 1951 | 0.83 | 0.73-0.94 | 1 | 0.96-1.05 |
| 1956 | 0.67 | 0.58-0.77 | 0.93 | 0.89-0.98 |
| 1961 | 0.58 | 0.49-0.70 | 0.79 | 0.74-0.84 |
| 1966 | 0.59 | 0.46-0.75 | 0.58 | 0.49-0.69 |
| 1971 | 0.63 | 0.40-1.02 | 0.64 | 0.58-0.72 |
| Nota: REF = referencia; IC = intervalo de confianza. | ||||
Tabla 2. Índices de tasas estimados e intervalos de conferencia del 95% para el efecto de la cohorte de nacimiento en la mortalidad por carcinoma hepatocelular de mujeres en Taiwán, 1891-1971.
Tabla complementaria 1. Haga clic aquí para descargar esta tabla.
Discusión
Debido a la tendencia temporal de la mortalidad por CHC, los modelos convencionales subestiman algunas características importantes ocultas en los datos (como los efectos de cohorte), y los análisis convencionales que utilizan la extrapolación lineal simple de la tasa de corrección de la edad logarítmica observada muestran una precisión significativamente menor en sus predicciones. Está claro que esta tendencia ha continuado durante 35 años y tenderá al alza en los próximos años si observamos directamente la tendencia a largo plazo de la mortalidad por CHC en Taiwán desde 1976 hasta 2015 (Figura 3). De hecho, la tendencia reciente de la mortalidad por CHC en Taiwán está disminuyendo y está impulsada por el efecto de cohorte (determinado por el análisis de APC), que, como se mencionó anteriormente, disminuyó después de la cohorte de 1936. Este estudio muestra que la aplicación del modelo APC proporciona advertencias avanzadas y más precisas sobre los cambios de tendencia.
Desde una perspectiva clínica, hay aproximadamente dos mil millones de personas infectadas por el virus de la hepatitis B (VHB) 12, y aproximadamente 350 millones de personas sufren como consecuencia de ello. En consecuencia, se trata de un importante problema de salud con alta morbilidad a nivel mundial. La infección por VHB causa una amplia gama de problemas clínicos, incluido el estado de portador ineficaz para fulminar la hepatitis, la cirrosis o el carcinoma hepatocelular. El método de prevención más eficaz es inocular a las personas con la vacuna contra la hepatitis B. Taiwán implementó el primer plan mundial de vacunación masiva contra la hepatitis B en 1984 13. En este programa, las mujeres embarazadas fueron examinadas para detectar el antígeno de superficie de la hepatitis B (HBsAg) y el antígeno de la envoltura de la hepatitis B (HBeAg) 14. Durante los primeros dos años de este programa, el programa de inmunización solo cubrió a los bebés de madres con HBsAg. Sin embargo, a partir del tercer año del programa de vacunación, todos los bebés estaban cubiertos. La tasa de cobertura de la vacuna contra la hepatitis B ha alcanzado el 99% en los últimos años 15. Casi el 90% al 95% de las personas experimentarán inmunidad de por vida después de recibir las tres dosis de la vacuna. Hacemos hincapié en que la disminución del CHC pediátrico en Taiwán se atribuye en gran medida a este programa mundial de vacunación.
El modelo de APC que se muestra en este artículo proporciona una advertencia anticipada sobre estos (aumentados) cambios de tendencia (que disminuirán en un futuro próximo). Al comparar la tendencia de los efectos de cohorte (Cuadros 1 y 2) y la mortalidad ajustada por edad (Figura 3), la tasa de mortalidad directa ajustada por edad (o tasa de mortalidad por estandarización por edad) fue la misma que el promedio ponderado. En este estudio, se ponderan las tasas de mortalidad por edad en función de la proporción del grupo de edad de interés, basándose en la Población Estándar Mundial de 2000 16 . Dado que la validación de los efectos de cohorte dominó el patrón más reciente de mortalidad por CHC, calculamos la mortalidad de CHC ajustada por edad para los datos actualizados (hasta 2011-2015). Interpretamos esto en el sentido de que la estimación media ponderada de las cohortes proporciona información confiable mientras se preparan las investigaciones para pronosticar la mortalidad futura del CHC. Los detalles sobre la predicción de la mortalidad por CHC están disponibles en nuestro estudio previo 5.
Una hipótesis general es que cada valor dentro de los datos proporciona la misma información para evaluar los parámetros de un modelo. Este enfoque se ha utilizado en la mayoría de los métodos de modelado (como los modelos de regresión lineal o no lineal) y significa que la desviación estándar del término de error es la variable predictora subyacente constante. Sin embargo, de acuerdo con nuestra revisión de la literatura, esta hipótesis no es adecuada para la modelización para estimar empíricamente los parámetros. Los parámetros desconocidos se estiman cuando usamos la regresión ponderada, que genera un peso menor con menos precisión para los puntos de datos y un peso grande con más precisión para los puntos de datos. El proceso de ponderación disminuyó la desviación estándar del estimador. Sin embargo, las deficiencias del método de regresión ponderada son casi desconocidas en la práctica empírica. Dado que no se conocen los pesos exactos, se utilizaron los pesos estimados para estimar los parámetros. Además, la experiencia previa ha demostrado que la ponderación basada en la estimación no cambia significativamente o suele afectar al análisis de regresión o a su interpretación 17. Hipotéticamente, el modelo APC puede adaptarse a cualquier enfermedad en la que la incidencia se vea afectada por la edad, el período y la cohorte. Además, se dispuso de estimaciones medias ponderadas para la predicción 18,19,20. Si el IC es comparativamente estrecho, la incertidumbre es pequeña. En vista del hecho de que el IC representa la incertidumbre inherente a este tipo de evaluación y los valores que contiene, generalmente concluimos que el uso del IC tiene un impacto sustancial.
La quimioembolización arterial transcatéter (TACE, por sus siglas en inglés) es uno de los métodos más eficaces para controlar clínicamente el CHC. Sin embargo, es difícil elegir este método como terapia principal o auxiliar, ya que no requiere cirugía abierta. El hígado suele proporcionar el 75% de la sangre y los nutrientes a través de la vena porta hepática, mientras que la arteria hepática proporciona el 25% de la sangre y los nutrientes. A diferencia de la sangre de la arteria hepática extraída de la mayoría de los CHC, este líquido aumenta rápidamente y rara vez proviene de la vena porta hepática. Además, este efecto es muy adecuado para el TACE porque el cáncer primario de hígado rara vez hace metástasis a otras partes del cuerpo. Aunque es poco probable que los tumores hepatocelulares malignos hagan metástasis, son difíciles de erradicar. En la práctica clínica, el seguimiento de los pacientes con CHC se realiza cada dos o tres meses. Una vez que se detecta una elevación anormal de la alfafetoproteína (AFP) o una ecografía anormal, se realizan una tomografía computarizada y una resonancia magnética. Si se descubre un nuevo tumor, se considerará el TACE. También se han desarrollado nuevos biomarcadores para detectar la recurrencia del CHC relacionado con el VHB, como el índice de tiempo cuantitativo del ADN del VHB (HDQTI) 21. El producto de los resultados del seguimiento y el logaritmo de la relación entre la carga de ADN del VHB detectada y normal es la suma de los HDQTI. El HDQTI se utiliza como indicador pronóstico independiente de la recidiva del CHC relacionado con el VHB 21.
Nuestro estudio tiene varias limitaciones. En primer lugar, nos limitamos a formular hipótesis sobre las etiologías de los cambios observados. Con el modelo APC, se reconsideró la mortalidad por CHC según la edad, el período y los efectos de la cohorte. Sin embargo, en este estudio, utilizamos como hipótesis la mediana del pulido. En segundo lugar, el análisis de APC se ha utilizado ampliamente en el campo de la epidemiología en países en desarrollo o recientemente desarrollados para estudios de cohortes a largo plazo. En tercer lugar, no dispusimos de información del conjunto de datos de formato acumulado para ajustar los factores de confusión en el modelo de APC, como las comorbilidades o el estilo de vida. Se necesitan datos aislados para futuras investigaciones que resuelvan esta limitación. En cuarto lugar, para modificar el procedimiento de regresión en el método polietápico, se utilizó como ponderación el número de muertes por CHC. Dado que no se conoce el peso exacto, el uso de varios pesos provoca una ligera inflación dentro de los efectos de cohorte estimados. En última instancia, existen varios métodos de estimación de APC para resolver el problema irreconocible (por ejemplo, Holford utiliza tendencias lineales y de curvatura para resolver el problema irreconocible 22). Al mismo tiempo, el pulido de la mediana proporciona supuestos complejos en forma de conversión conceptual entre los modelos de APC para evaluar el efecto de cohorte con el menor número de supuestos y aplica fácilmente un formato común para las tablas de contingencia.
En general, la estimación ponderada permitió que el efecto medio ponderado con un IC comparativamente estrecho de cada cohorte modificara el modelo de regresión. En resumen, para los métodos polietápicos, se recomienda utilizar estimaciones ponderadas de modelos de regresión para evaluar los efectos de cohorte en los datos de la tabla de contingencia por edad-período.
Divulgaciones
Los autores no tienen nada que revelar.
Agradecimientos
Este trabajo fue apoyado por el Hospital Tzu Chi de Taipei TCRD-TPE-109-RT-8 (2/3) y TCRD-TPE-109-39 (2/2).
Materiales
| Name | Company | Catalog Number | Comments |
| not applicable | not applicable | not applicable | not applicable |
Referencias
- Kuntz, E., Kuntz, H. D. Hepatology: Principles and Practice. , Springer. New York. 774(2006).
- McGlynn, K. A., et al. International trends and patterns of primary liver cancer. International Journal of Cancer. 94 (2), 290-296 (2001).
- Bosch, F. X., Ribes, J., Diaz, M., Cleries, R. Primary liver cancer: worldwide incidence and trends. Gastroenterology. 127, 5-16 (2004).
- Tzeng, I. S., Ng, C. Y., Chen, J. Y., Chen, L. S., Wu, C. C. Using weighted regression model for estimating cohort effect in age-period contingency table data. Oncotarget. 9 (28), 19826-19835 (2018).
- Tzeng, I. S., Lee, W. C. Forecasting hepatocellular carcinoma mortality in Taiwan using an age-period-cohort model. Asia-Pacific Journal of PublicHealth. 27, 65-73 (2015).
- Tzeng, I. S., et al. Predicting emergency departments visit rates from septicemia in Taiwan using an age-period-cohort model, 1998 to 2012. Medicine. 95, 5598(2016).
- Chen, S. H., et al. Period and Cohort Analysis of Rates of Emergency Department Visits Due to Pneumonia in Taiwan, 1998-2012. Risk Management and Healthcare Policy. 13, 1459-1466 (2020).
- Keyes, K. M., Li, G. A multiphase method for estimating cohort effects in age-period contingency table data. Annals of Epidemiology. 20, 779-785 (2010).
- Tukey, J. Exploratory data analysis Reading: MS. , Addison-Wesley Publishing Company. (1977).
- Selvin, S. Statistical analysis of epidemiologic data. , University Press. New York: Oxford. (1996).
- Légaré, G., Hamel, D. An age-period-cohort approach to analyzing trends in suicide in Quebec between 1950 and 2009. Canadian Journal of Public Health. 104, 118-123 (2013).
- Lavanchy, D. Hepatitis B virus epidemiology, disease burden, treatment, and current and emerging prevention and control measures. Journal of Viral Hepatitis. 11, 97-107 (2004).
- Chang, M. H., et al. Universal hepatitis B vaccination in Taiwan and the incidence of hepatocellular carcinoma in children. Taiwan Childhood Hepatoma Study Group. New England Journal of Medicine. 336, 1855-1859 (1997).
- Lu, F. T., Ni, Y. H. Elimination of mother-to-infant transmission of hepatitis B virus: 35 years of experience. Pediatric Gastroenterology, Hepatology & Nutrition. 23 (4), 311-318 (2020).
- Chien, Y. C., Jan, C. F., Kuo, H. S., Chen, C. J. Nationwide hepatitis B vaccination program in Taiwan: effectiveness in the 20 years after it was launched. Epidemiologic Reviews. 28, 126-135 (2006).
- Ahmad, O. B., et al. Age standardization of rates: a new WHO standard. Geneva: GPE Discussion Paper Series. World Health Organization. , 31(2005).
- da Silva, C. P., Emídio, E. S., de Marchi, M. R. Method validation using weighted linear regression models for quantification of UV filters in water samples. Talanta. 131, 221-227 (2015).
- Dawes, R. M. The robust beauty of improper linear models in decision making. American Psychologist. 34, 571-582 (1979).
- Dawes, R. M., Corrigan, B. Linear models in decision making. Psychological Bulletin. 81, 95-106 (1974).
- Einhorn, H. J., Hogarth, R. M. Unit weighting schemes for decision making. Organizational Behavior and Human Performance. 13, 171-192 (1975).
- Wang, W., et al. Association of hepatitis B virus DNA level and follow-up interval with hepatocellular carcinoma recurrence. JAMA Network Open. 3 (4), 203707(2020).
- Holford, T. R. The estimation of age, period and cohort effects for vital rates. Biometrics. 39, 311-324 (1983).
Reimpresiones y Permisos
Solicitar permiso para reutilizar el texto o las figuras de este JoVE artículos
Solicitar permisoThis article has been published
Video Coming Soon
ACERCA DE JoVE
Copyright © 2025 MyJoVE Corporation. Todos los derechos reservados