הפרעות עקיפה

גל הוא תנודה במשרעת של כמות פיזית כלשהי בחלל ו /או בזמן. גלים או חלקים שונים של גלים יכולים לחפוף ו"להפריע " כדי לייצר משרעת חזקה וחלשה לסירוגין. הפרעה היא אחת התופעות האופייניות ביותר הקשורות לגלים. שקול דוגמה פשוטה לשני גלים המתפשטים לאורך קו בעל ממד אחד (ציר x) ומיוצגים מתמטית על-ידי:

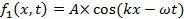
ו

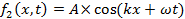
התפשטות ימינה (+x כיוון) ושמאל (−x כיוון), בהתאמה. כאן, A הוא משרעת השיא, ו- k הוא "מספר הגל" או "וקטור הגל" המוגדר כ,

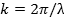
כאשר λ הוא אורך הגל (תקופתיות מרחבית של הגל). ω מוגדר כ,

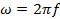
כאשר f הוא התדירות ו,

כאשר T היא התקופה (בזמן) של הגל. כאשר שני הגלים חופפים, המשרעת שלהם מסתכמת (הידועה בשם "עיקרון הסופרפוזיציה של הגל") כדי לתת:

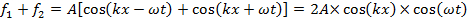
אשר ידוע גם בשם "גל עומד". באותם מקומות שבהם,

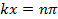
(כאשר n הוא מספר שלם) ו,

התנודות (כפונקציות של זמן t) תהיה משרעת מקסימלית (בין −2A ו +2A). לעומת זאת, במקומות שבהם,

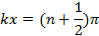
ו

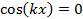
התנודות יהיו אפס (ולכן מינימלי) משרעת (הידוע גם בשם "צמתים"). שינוי מרחבי כזה של משרעת גל חזקה וחלשה מייצג "דפוס הפרעה". תופעה זו יכולה להיות כללית לגלים במרחב דו-ממדי ותלת ממדי. הוא גם עומד בבסיס התופעות של עקיפה חד-חריצית והפרעה כפולה של אור (שהוא גל אלקטרומגנטי) שניתן לראות בניסוי זה.

אם אור אורך הגל (λ) נוצץ על חריץ צר של רוחב (א) (מוצג באופן סכמטי באיור 1a),עוצמת האור (שהיא פרופורציונלית לריבוע של משרעת השיא של הגל) הרחק מהחריץ תחליף בין ערכים גדולים וקטנים (כמעט אפסיים), המתאימים לאזורים "בהירים" ו"כהים", לאורך כיוון הרוחב ("ציר y" באיור 1a) של החריץ. שינוי זה, המכונה "דפוס העקיפה" של האור (דרך צמצם קטן), הוא גם תופעה אופיינית לגלים. ביסודו של דבר, הוא נובע מההתערבות בין חלקים שונים של גל האור לאחר הצמצם (בפרט, נקודות בין שני הקצוות של הצמצם "פולטים מחדש" את גל האור לכיוונים שונים). השונות הזוויתית של עוצמת האור מסומנת כ- I(θ), כאשר θ מייצג את זווית הכיוון (לכיוון +y או -y) הרחק מהכיוון "ישר דרך", דרך y = 0 באיור 1a). עבור θ קטן, ניתן להראות כי אני(θ) הוא פרופורציונלי בערך |sin(πaθ/λ)/(πaθ/λ)|2. כלומר, "כהה" ל,

ו"בהיר עבור,

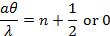
. אם המסך ממוקם במרחק L מהחריץ, נצפים לסירוגין שוליים בהירים וכהים במיקומים שונים של y (כל שוליים יפעלו במקביל לחתוך) כפי שמוצג בסכמטית באיור 1b (משמאל). עבור θ קטן (קרוב למרכז y = 0),

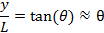
כך ניתן לתאר את עוצמת השוליים בערך,

(פונקציה זו מוצגת באופן סכמטי באיור 1b, מימין). המרכז y = 0 הוא תמיד שוליים בהירים (שכן החטא(t)/t יש מקסימום של 1 כאשר t→0 ויורד באופן מונוטוני עד 0 כמו t עולה מ 0 π). מתרחקים מהמרכז, השוליים הכהים "מסדר ראשון" נתקלים במרכז,

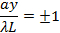
ואז שוליים בהירים מרוכזים ב,

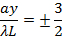
ואז השוליים הכהים שוב מרוכזים ב,

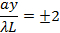
ואז שוליים בהירים שוב מרוכזים ב,

וכן הלאה. הרוחב של כל שוליים בהירים מחוץ למרכז הוא בערך λL/ a, למעט השוליים הבהירים המרכזיים שרוחבו כפליים (רוחב ~ 2λL/a, או ההפרדה בין שני שוליים כהים מסדר ראשון ב- ± λL/ a). ככל שהצמצום צר יותר, או ככל שאורך הגל גדול יותר או מרחק המסך L, כך השוליים יהיו מפוזרים יותר.

אם האור נוצץ דרך שני חריצים צרים מופרדים זה לזה עם הפרדה d (המתוארת באופן סכמטי באיור 2a)במערך דומה לזה באיור 1, ניתן להבחין ב"תבנית הפרעת החריץ הכפולה" המפורסמת של יאנג (מוצגת באופן סכמטי באיור 2b). ניתן להראות כי עבור θ קטן (קרוב למרכז y = 0), שוליים בהירים מרוכזים ב,

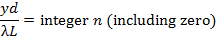
ושוליים כהים מרוכזים ב,

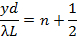
ניתן לצפות. בניגוד לתבנית עקיפה אחת החתכה שנדונו לעיל, כאן כל השוליים האור (כולל המרכזי ב y = 0), יש רוחב שווה והם מרווחים באותה מידה על ידי λL/ d. החריץ הצר עדיין ייצור דפוסי עקיפה, אך בדרך כלל רוחב החריץ (א) קטן בהרבה מההפרדה (ד),ואפנון העוצמה (בשל תבנית ההפרשה) יעלה על שולי ההפרעה הכפולה הקרובים והמרווחים באותה מידה.

מקור האור בדיון הנ"ל נחשב למונוכרומטי לחלוטין (כלומר יש לו אורך גל מוגדר היטב) וקוהרנטי (כלומר אם המיידיים שתנודות הגל מגיע למקסימום או למינימום במיקום אחד ידועים, ניתן לחזות את המיידיים שבהם ניתן יהיה לחזות את המקסימום או המינימום בכל מקום אחר). זהו המקרה לדוגמה, אם הגל מתואר על-ידי פונקציית קוסינוס כ- cos(kx−ωt+φ) עם שלב אחיד, קבוע φ, אשר ניתן לבחור להיות אפס על ידי הגדרה מחדש של נקודת ההתחלה של הזמן. מכיוון שלייזר הוא הקירוב הטוב ביותר לסוג זה של מקור אור אידיאלי, קרן לייזר משמשת כמקור האור בניסוי זה (מבחינה היסטורית בזמן טרום הלייזר, ניסויים כאלה השתמשו במקור אור דמוי נקודה כמו זה המיוצר על ידי אור חולף למרות חור קטן).

חשוב לציין כי השוליים העקיפה וההפרעה בפועל (כולל הצורה והעוצמה של השוליים) יכולים להיראות מסובכים יותר ופחות "אידיאליים" מאלה המתוארים לעיל במקרים והעריפות הפשוטים ביותר, בשל פגמים במקור האור כמו גם בחתכים. לדוגמה, ניתן להפחית את הניגודיות בין השוליים (כך שהשוליים ה"כהים" לא באמת מגיעים לאפס עוצמה) אם מקור האור פחות קוהרנטי. מצד שני, המיקום והמרווח של השוליים בדרך כלל צפויים היטב על ידי המודל הפשוט שנדון לעיל.
 

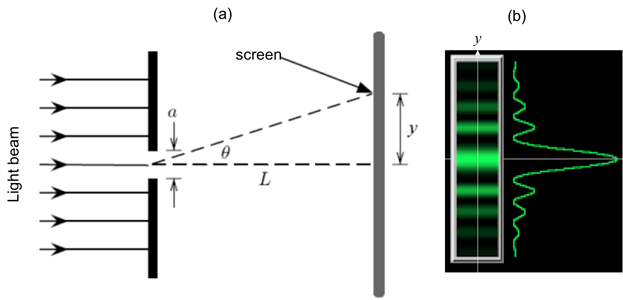
איור 1: עקיפה אחת. (א)תרשים סכמטי של ההתקנה האופטית, עם אור זורח דרך חריץ צר של רוחב a, ומסך תצפית הממוקם במרחק L משם; וכן (b)תבנית סטייה סכמטית מהשוליים שניתן לראות על המסך (משמאל) וריאציה תואמת של עוצמת האור כפונקציה של מרחק אנכי (y) הרחק מהמרכז.

 
איור 2: הפרעה כפולה לחתוך. (א)תרשים סכמטי של ההתקנה האופטית, עם אור זורח דרך שני חריצים צרים המופרדים על-ידי מרחק d, ומסך תצפית הממוקם במרחק L משם; נוסף (ב)שולי הפרעה סכמטית (במרווחים שווים) שניתן לצפות בהם על המסך.

בשלב 2.3 מוצגת תבנית אור מייצגת שניתן לראות על הקיר באיור 3ב, המציג את השוליים האופייניים לעקיפה. שים לב שהשוליים הבהירים המרכזיים רחבים בערך פי שניים (בכיוון y)מהשוליים הבהירים האחרים (שהם בערך זהים ברוחבם), ועוצמת היתר של השוליים הבהירים נרקבת מהמרכז לאורך ציר ה- y,כצפוי לתבנית עקיפה אחת.

בשלב 3.3 מוצגת תבנית אור מייצגת שניתן לראות על הקיר באיור 4ב. יש תבנית אפנון בעוצמה כוללת שנראית דומה לתבנית עקיפה שנצפתה בשלב 2.3. זהו אכן דפוס עקיפה בשל כל אחד מהחריץ הצר. בתוך האזורים הבהירים של תבנית ההפשטה, ניתן לצפות בפסים בהירים במרווחים שווים. אלה הם השוליים הפרעת חריץ כפול. שולי הפרעה אלה צרים בהרבה מהאזורים הבהירים של תבנית ההפרשה מכיוון שההפרדה הבין-חריץ d גדולה בהרבה מרוחב החריץ a (ההדדיות של אורכים אלה שולטות ברוחב ההפרעה או בשולי עקיפה, בהתאמה).

איור 3. תרשים המציג: (א) קרן לייזר זורחת על חריץ יחיד על רדיד אלומיניום, אשר קבוע על קרטון עם חור פתוח; ות"ב) שולי עקיפה מייצגים שנצפו על מסך לאחר החריץ.

איור 4. תרשים המציג: (א) קרן לייזר זורחת על חריצים כפולים על רדיד אלומיניום, אשר קבוע על קרטון עם חור פתוח; ות"ב) שולי הפרעה מייצגים שנצפו על המסך לאחר החריץ הכפול.

בניסוי זה, הדגמנו את תבנית עקיפה אחת חריץ דפוס הפרעה חריץ כפול של אור, באמצעות קרן לייזר. התבוננות בתופעות גל אופייניות אלה ממחישה את אופי הגל של האור.

עקיפה והפרעה של אור שיחקו תפקידים חיוניים בהתפתחות האופטיקה כפי שהם עזרו לקבוע כי האור הוא גל אלקטרומגנטי. השפעות אלה חשובות גם בטכנולוגיות רבות המבוססות על אופטיקה ופוטוניקה. לדוגמה, עקיפה משמשת בדרך כלל למדידת גודל של עצם קטן או חורים קטנים, והיא גם היבט חשוב שיש לקחת בחשבון בעת תכנון מיקרוסקופים אופטיים ומערכות הדמיה. מדידת הפרעות אופטיות (המכונות "אינטרפרומטריה") יכולה לשמש למדידה מדויקת של מרחקים (כגון אלה שבין מקורות אור או מראות) ומצאה יישומים החל עיבוד שבבי, גיאולוגיה ואסטרונומיה (כגון בפרויקט LIGO שזיהה גלי כבידה).

מחבר הניסוי מכיר בסיועו של גארי הדסון להכנת חומר וצ'ואנחסון לי על כך שהדגים את הצעדים בסרטון.