JoVE Science Education
Physics II
Hai accesso completo a questo contenuto tramite
Nanyang Technological UniversityInterferenza e diffrazione
Panoramica
Fonte: Yong P. Chen, PhD, Dipartimento di Fisica e Astronomia, College of Science, Purdue University, West Lafayette, IN
Interferenze e diffrazione sono fenomeni caratteristici delle onde, che vanno dalle onde d'acqua alle onde elettromagnetiche come la luce. L'interferenza si riferisce al fenomeno di quando due onde dello stesso tipo si sovrappongono per dare una variazione spaziale alternata di ampiezza d'onda grande e piccola. La diffrazione si riferisce al fenomeno di quando un'onda passa attraverso un'apertura o gira intorno a un oggetto, diverse parti dell'onda possono interferire e anche dare origine a un'alternanza spaziale di grande e piccola ampiezza.
Questo esperimento dimostrerà la natura ondulatoria della luce osservando la diffrazione e l'interferenza di una luce laser che passa attraverso una singola fessura e doppie fessure, rispettivamente. Le fessure vengono semplicemente tagliate usando lame di rasoio in un foglio di alluminio e i caratteristici modelli di diffrazione e interferenza si manifestano come modelli di alternanza di frange chiare e scure su uno schermo posto dopo il foglio, quando la luce viene illuminata attraverso le fessure sul foglio. Storicamente, l'osservazione della diffrazione e dell'interferenza della luce ha svolto un ruolo importante nello stabilire che la luce è un'onda elettromagnetica.
Principi
Un'onda è un'oscillazione nell'ampiezza di una certa quantità fisica nello spazio e/o nel tempo. Onde o diverse parti di onde possono sovrapporsi e "interferire" per produrre un'ampiezza forte e debole alternata. L'interferenza è uno dei fenomeni più caratteristici associati alle onde. Si consideri un semplice esempio di due onde che si propagano lungo una linea unidimensionale (asse x) e rappresentate matematicamente da:
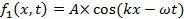
e
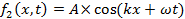
propagazione a destra (direzione +x) e sinistra (direzione −x), rispettivamente. Qui, A è l'ampiezza del picco e k è il "numero d'onda" o "vettore d'onda" definito come,
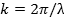
dove λ è la lunghezza d'onda (periodicità spaziale dell'onda). ω è definito come,
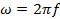
dove f è la frequenza e,

dove T è il periodo (nel tempo) dell'onda. Quando le due onde si sovrappongono, le loro ampiezze si sommano (che è noto come il "principio di sovrapposizione dell'onda") per dare:
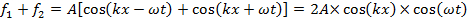
che è anche conosciuta come "onda stazionaria". In quei luoghi in cui,
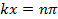
(dove n è un numero intero) e,

le oscillazioni (come funzioni del tempo t) avranno ampiezza massima (tra −2A e +2A). Al contrario, in luoghi in cui,
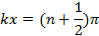
e
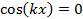
le oscillazioni avranno ampiezza zero (quindi minima) (note anche come "nodi"). Tale alternanza spaziale di ampiezza d'onda forte e debole rappresenta un "modello di interferenza". Questo fenomeno può essere generalizzato alle onde nello spazio bidimensionale e tridimensionale. È anche alla base dei fenomeni di diffrazione a fessura singola e interferenza a doppia fessura della luce (che è un'onda elettromagnetica) da osservare in questo esperimento.
Se la luce della lunghezza d'onda (λ) è illuminata su una stretta fessura di larghezza (a) (mostrata schematicamente in Figura 1a), l'intensità luminosa (che è proporzionale al quadrato dell'ampiezza di picco dell'onda) lontana dalla fessura si alternerà tra valori grandi e piccoli (quasi zero), corrispondenti a regioni "luminose" e "scure", lungo la direzione della larghezza ("asse y" in Figura 1a) della fessura. Questa alternanza, nota come "modello di diffrazione" della luce (attraverso una piccola apertura), è anche un fenomeno caratteristico per le onde. Fondamentalmente, nasce dall'interferenza tra diverse parti dell'onda luminosa dopo l'apertura (in particolare, i punti tra i due bordi dell'apertura "riemetteranno" l'onda luminosa verso direzioni diverse). La variazione angolare dell'intensità luminosa è indicata come I(θ), dove θ rappresenta l'angolo della direzione (verso +y o –y) lontano dalla direzione "dritta", attraverso y = 0 nella Figura 1a). Per il piccolo θ, si può dimostrare che I(θ) è approssimativamente proporzionale a |sin(πaθ/λ)/(πaθ/λ)|2. Cioè, "buio" per,

e "luminoso per,
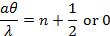
. Se lo schermo è posizionato a distanza L dalla fessura, si osservano frange alternate chiare e scure in diverse posizioni di y (ogni frangia correrà parallela alla fessura), come schematicamente mostrato nella Figura 1b (a sinistra). Per θ piccolo (vicino al centro y = 0),
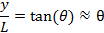
quindi l'intensità delle frange può essere approssimativamente descritta come,

(questa funzione è schematicamente mostrata nella Figura 1b, a destra). Il centro y = 0 è sempre una frangia luminosa (poiché sin(t) /t ha un massimo di 1 quando t →0 e diminuisce monotonamente fino a 0 mentre t aumenta da 0 a π). Allontanandosi dal centro, le frange scure del "primo ordine" si incontrano centrate su,
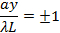
poi frange luminose centrate a,
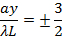
poi frange scure di nuovo centrate a,
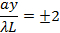
Poi frange luminose di nuovo centrate su,

E così via. La larghezza di ogni frangia luminosa al di fuori del centro è di circa λL/a, ad eccezione della frangia luminosa centrale che è due volte più larga (larghezza ~2 λL/a, o la separazione tra due frange scure del primo ordine a ± λL/a). Più stretta è la fessura, o maggiore è la lunghezza d'onda λ o la distanza dello schermo L, più diffuse saranno le frange.
Se la luce viene illuminata attraverso due fessure strette strettamente separate con separazione d (schematicamente raffigurata nella Figura 2a)in una configurazione altrimenti simile a quella della Figura 1,si può osservare il famoso "modello di interferenza a doppia fessura di Young" (schematicamente mostrato nella Figura 2b). Si può dimostrare che per piccoli θ (vicino al centro y = 0), frange luminose centrate a,
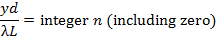
e frange scure centrate su,
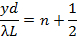
può essere osservato. In contrasto con il modello di diffrazione a fessura singola discusso sopra, qui tutte le frange di luce (compresa quella centrale a y = 0), hanno larghezze uguali e sono ugualmente distanziate da λL/ d. Le fessure strette produrranno ancora modelli di diffrazione, ma di solito la larghezza della fessura (a) è molto più piccola della separazione (d), e la modulazione dell'intensità (a causa del modello di diffrazione) si sovrapporrà alle frange di interferenza a doppia fessura molto più vicine e ugualmente distanziate.
Si presume che la sorgente luminosa nella discussione di cui sopra sia perfettamente monocromatica (nel senso che ha una lunghezza d'onda ben definita λ) e coerente (il che significa che se gli istanti in cui l'oscillazione dell'onda raggiunge il massimo o il minimo in una posizione sono noti, gli istanti in cui il massimo o il minimo saranno raggiunti in qualsiasi altra posizione possono essere previsti). Questo è il caso, ad esempio, se l'onda è descritta da una funzione coseno come cos(kx−ωt+φ) con una fase uniforme e costante φ, che può essere scelta per essere zero ridefinendo il punto di partenza del tempo. Poiché un laser è la migliore approssimazione per questo tipo di sorgente luminosa ideale, un raggio laser viene utilizzato come fonte di luce in questo esperimento (storicamente nel tempo pre-laser, tali esperimenti hanno utilizzato una fonte di luce simile a un punto come quella prodotta facendo passare la luce attraverso un piccolo foro).
È importante notare che le frange di diffrazione e interferenza effettive (compresa la forma e l'intensità delle frange) possono sembrare più complicate e meno "ideali" di quelle sopra descritte in questi casi e approssimazioni più semplici, a causa di imperfezioni nella sorgente luminosa e nelle fessure. Ad esempio, il contrasto delle frange può essere ridotto (in modo tale che le frange "scure" non raggiungano realmente l'intensità zero) se la sorgente luminosa è meno coerente. D'altra parte, le posizioni e la spaziatura delle frange sono solitamente ben previste dal semplice modello discusso sopra.
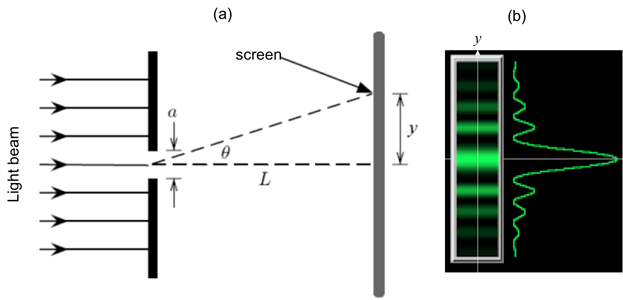
Figura 1: Diffrazione a fessura singola. a) Schema schematico dell'impostazione ottica, con la luce che splende attraverso una stretta fessura di larghezza a e uno schermo di osservazione situato a distanza L; e (b) Schema schematico di frange di diffrazione che può essere osservato sullo schermo (a sinistra) e corrispondente variazione dell'intensità luminosa in funzione della distanza verticale (y) dal centro.

Figura 2: Interferenza a doppia fessura. a) Schema schematico dell'impostazione ottica, con la luce che splende attraverso due fessure strette separate dalla distanza d e uno schermo di osservazione situato a distanza L; e (b) Frange di interferenza schematica (equamente distanziate) che possono essere osservate sullo schermo.
Procedura
1. Acquisizione dei componenti richiesti per l'esperimento
- Ottenere occhiali di sicurezza laser e indossare durante questo esperimento prima di accendere il laser.
- Procuratevi un pezzo di foglio di alluminio e usate le forbici per tagliarlo in due (circa) 2 x 2 in pezzi quadrati.
- Ottenere due cartoni, ciascuno di circa 3 x 3 pollici, con un foro (diametro circa 1 in) tagliato nel mezzo.
- Ottenere un dispositivo in grado di bloccare il cartone o un blocco a cui il cartone può essere nastrato.
- Ottenere alcune sottili lame di rasoio.
- Ottenere un puntatore laser He-Ne con lunghezza d'onda ~ 633 nm o puntatore laser verde con lunghezza d'onda di 532 nm.
2. Diffrazione a fessura singola
- Prendi un foglio di alluminio quadrato e usa una lama di rasoio per tagliare una fessura lunga circa 1 cm al centro del foglio. Usa un righello per aiutare a guidare il rasoio per ottenere un taglio dritto.
- Fissare la lamina su un quadrato di cartone con la fessura orientata orizzontalmente all'interno del foro aperto (schematicamente mostrato nella Figura 3a). Metti del nastro adesivo intorno agli angoli della lamina (non coprire la fessura). Il cartone aiuta a stabilizzare la lamina durante questo esperimento. Blocca un bordo del cartone con il dispositivo (il cartone deve essere perpendicolare alla superficie del tavolo), con il foro e la fessura orizzontale esposti e di fronte a un muro bianco (che sarà lo schermo) a circa 30 cm di distanza.
- Accendere il puntatore laser e far brillare il raggio laser (propagandosi nella direzione normale alla lamina) sulla fessura. Osserva il modello di luce sul muro dall'altra parte della lamina. Spegni la luce della stanza per una migliore visibilità del modello.
3. Interferenza a doppia fessura
- Prendi l'altro foglio di alluminio. Impilare 3 lame di rasoio insieme ma con il bordo della lama centrale incassato dai bordi delle altre due lame. Usa questa pila per tagliare due fessure strettamente distanziate al centro della lamina (ciascuna lunga circa 1 cm). Usa un righello per aiutare a guidare il rasoio e fare un taglio dritto.
- Fissare la lamina sull'altro cartone (schematicamente mostrato nella Figura 4a) e di nuovo sostenere il cartone con la morsa o il blocco, simile al passaggio 2.2.
- Accendere il puntatore laser e far brillare il raggio laser sulla doppia fessura. Osserva il modello di luce sul muro dall'altra parte della lamina. Spegni la luce della stanza per una migliore visibilità del modello.
Risultati
Per il passaggio 2.3, un modello di luce rappresentativo che può essere osservato sulla parete è mostrato nella Figura 3b, che mostra le caratteristiche frange di diffrazione. Si noti che la frangia luminosa centrale è circa due volte più larga (nella direzione y)delle altre frange luminose (che sono circa la stessa in larghezza) e la sovra intensità delle frange luminose decade dal centro lungo l'asse y,come previsto per il modello di diffrazione a fessura singola.
Per il passaggio 3.3, un modello di luce rappresentativo che può essere osservato sulla parete è mostrato nella Figura 4b. Esiste un modello di modulazione dell'intensità complessivo che sembra simile al modello di diffrazione osservato nel passaggio 2.3. Questo è infatti il modello di diffrazione dovuto a ciascuna delle fessure strette. All'interno delle regioni luminose del modello di diffrazione, si possono osservare strisce luminose approssimativamente equamente distanziate. Queste sono le frange di interferenza a doppia fessura. Queste frange di interferenza sono molto più strette delle regioni luminose del modello di diffrazione perché la separazione inter-fessura d è molto più grande della larghezza della fessura a (il reciproco di queste lunghezze controlla rispettivamente le larghezze delle frange di interferenza o diffrazione).

Figura 3. Diagramma che mostra:(a) unraggio laser che brilla su una singola fessura su un foglio di alluminio, che è fissato su cartone con un foro aperto; e (b) frange di diffrazione rappresentative osservate su uno schermo dopo la fessura. 
Figura 4. Diagramma che mostra:(a) unraggio laser che brilla su doppie fessure su foglio di alluminio, che è fissato su cartone con un foro aperto; e(b)frange di interferenza rappresentative osservate su uno schermo dopo le doppie fessure.
Applicazione e Riepilogo
In questo esperimento, abbiamo dimostrato il modello di diffrazione a singola fessura e il modello di interferenza a doppia fessura della luce, utilizzando un raggio laser. L'osservazione di questi fenomeni ondulatori caratteristici dimostra la natura ondulatoria della luce.
La diffrazione e l'interferenza della luce hanno svolto un ruolo essenziale nello sviluppo dell'ottica in quanto hanno contribuito a stabilire che la luce è un'onda elettromagnetica. Questi effetti sono importanti anche in molte tecnologie basate sull'ottica e sulla fotonica. Ad esempio, la diffrazione è comunemente usata per misurare le dimensioni di un piccolo oggetto o di piccoli fori ed è anche un aspetto importante da considerare quando si progettano microscopi ottici e sistemi di imaging. La misurazione delle interferenze ottiche (la cosiddetta "interferometria") può essere utilizzata per la misurazione di precisione delle distanze (come quelle tra sorgenti luminose o specchi) e hanno trovato applicazioni che vanno dalla lavorazione, alla geologia e all'astronomia (come nel progetto LIGO che ha rilevato onde gravitazionali).
L'autore dell'esperimento riconosce l'assistenza di Gary Hudson per la preparazione del materiale e Chuanhsun Li per aver dimostrato i passaggi del video.
Tags
Vai a...
Video da questa raccolta:

Now Playing
Interferenza e diffrazione
Physics II
91.1K Visualizzazioni

Campi elettrici
Physics II
77.5K Visualizzazioni

Potenziale elettrico
Physics II
104.7K Visualizzazioni

Campi magnetici
Physics II
33.5K Visualizzazioni

Carica elettrica in un campo magnetico
Physics II
33.7K Visualizzazioni

Leggi di Ohm per conduttori ohmici e non ohmici
Physics II
26.2K Visualizzazioni

Resistori in serie e in parallelo
Physics II
33.1K Visualizzazioni

Capacità
Physics II
43.8K Visualizzazioni

Induttanza
Physics II
21.6K Visualizzazioni

Circuiti elettrici RC/RL/LC
Physics II
142.9K Visualizzazioni

Semiconduttori
Physics II
29.8K Visualizzazioni

Effetto fotoelettrico
Physics II
32.7K Visualizzazioni

Riflessione e rifrazione
Physics II
36.1K Visualizzazioni

Onde stazionarie
Physics II
49.8K Visualizzazioni

Onde sonore e effetto Doppler
Physics II
23.4K Visualizzazioni
Copyright © 2025 MyJoVE Corporation. Tutti i diritti riservati
Utilizziamo i cookies per migliorare la tua esperienza sul nostro sito web.
Continuando a utilizzare il nostro sito web o cliccando “Continua”, accetti l'utilizzo dei cookies.