קביעת ספקטרופוטומטריה של קבוע שיווי משקל
Overview
מקור: המעבדה של ד"ר מייקל אוונס — המכון הטכנולוגי של ג'ורג'יה
קבוע שיווי המשקל, K, עבור מערכת כימית הוא היחס בין ריכוזי המוצר לריכוזים מגיבים בשיווי משקל, כל אחד מהם הועלה לעוצמה של מקדמי הסטויצ'יומטריים שלהם. מדידת K כרוכה בקביעת ריכוזים אלה עבור מערכות בשיווי משקל כימי.
ניתן לחקור מערכות תגובה המכילות רכיב צבעוני יחיד באופן ספקטרופוטומטרי. הקשר בין ספיגה לריכוז עבור הרכיב הצבעוני נמדד ומשמש לקביעת ריכוזו במערכת התגובה של העניין. ריכוזים של הרכיבים חסרי הצבע ניתן לחשב בעקיפין באמצעות המשוואה הכימית המאוזנת ואת הריכוז הנמדד של הרכיב הצבעוני.
בסרטון זה, עקומת חוק הבירה עבור Fe(SCN)2+ נקבעת אמפירית ומוחלת על מדידת K לתגובה הבאה:

ארבע מערכות תגובה עם ריכוזים ראשוניים שונים של מגיבים נחקרות כדי להמחיש כי K נשאר קבוע ללא קשר לריכוזים הראשוניים.
Principles
כל תגובה כימית קשורה עם שיווי משקל קבוע K, אשר משקף את היחס בין ריכוזי המוצר לריכוזים מגיבים בשיווי משקל כימי. עבור התגובה הכללית A + b B  C C + d D, קבוע שיווי המשקל מוגדר כ
C C + d D, קבוע שיווי המשקל מוגדר כ

שבו הריכוזים בצד ימין של המשוואה הם טחנות בשיווי משקל. משוואה זו ידועה כביטוי שיווי המשקל לתגובה. במערכות כימיות שאינן בשיווי משקל, התגובות קדימה ואחורה מתרחשות בקצבים שונים עד שריכוזים של מגיבים ומוצרים מספקים את ביטוי שיווי המשקל.
כדי למדוד את הערך של K עבור מערכת בשיווי משקל כימי, יש צורך לקבוע את הריכוזים של מגיבים ומוצרים במישרין או בעקיפין. שיטות ספקטרופוטומטריות לקביעת K כרוכות במדידה ישירה של הריכוז של רכיב צבעוני אחד ומדידה עקיפה של האחרים. ספקטרוסקופיה גלויה של הרכיב הצבעוני בריכוזים ידועים מגלה את הקשר בין ספיגה לריכוז עבור רכיב זה. על פי החוק של באר, לקשר זה יש את הטופס
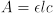
כאשר e הוא ספיגת הטוחנת של הרכיב ב L / מול-ס"מ, l הוא אורך הנתיב של אור דרך המדגם בס"מ, c הוא הטוחנת של הרכיב מול / L, ו- A הוא הספיגה.
ניתן להחיל את עקומת החוק של הבירה על הרכיב הצבעוני על מערכת תגובה בשיווי משקל כדי לקבוע את ריכוז הרכיב הזה ממדידות ספיגה (איור 1). לאחר מכן ניתן לחשב את הריכוזים של המגיבים והמוצרים הנותרים על ידי התאמת הריכוזים הראשוניים בהתבסס על הטוחנת הנמדדת של המינים הצבעוניים.
המערכת שנחקרה כאן היא התגובה של cation ברזל (III) עם אניון תיוצינאט כדי ליצור קומפלקס תיוצינאט ברזל (III).

ביטוי שיווי המשקל עבור מערכת תגובה זו הוא

כאשר הכתב התת-קרקעי eq מציין ריכוזי שיווי משקל. המוצר תיוציאנט ברזל (III) הוא כתום, אבל שני המגיבים הם חסרי צבע פתרון מימי. לפיכך, [Fe(SCN)2+]eq ניתן לקבוע ישירות ממדידות ספיגה.

ריכוזי שיווי משקל של המגיבים ניתן לחשב על ידי חיסור ריכוז שיווי המשקל של המוצר מהריכוזים הראשוניים של המגיבים. טבלה ראשונית-שינוי-שיווי משקל (ICE) ממחישה כיצד ריכוזי ראשוניים ושיווי משקל קשורים(טבלה 1).

ניסויים חוזרים ונשנים של ניסוי זה הכולל ריכוזים ראשוניים שונים של מגיבים צריכים להניב את אותו ערך של K, שכן הערך של K אינו תלוי בריכוז.
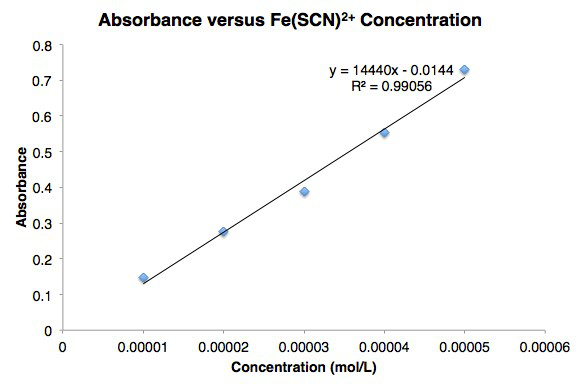
איור 1. עקומת חוק הבירה עבור ברזל (III) תיוציאנט.
| Fe3+ | SCN– | Fe (SCN)2+ | |
| הראשונית | [Fe3+] i | [SCN–] i | 0 |
| שינוי | –[Fe(SCN)2+]eq | –[Fe(SCN)2+]eq | +[Fe(SCN)2+]eq |
| שיווי משקל | [Fe3+] i – [Fe(SCN)2+]eq | [SCN–] i – [Fe(SCN)2+]eq | [Fe(SCN)2+] eq |
טבלה 1. טבלת שיווי משקל ראשוני-שינוי(ICE) הממחישה כיצד ריכוזי ראשוניים ושיווי משקל קשורים.
Procedure
1. קביעת עקומת חוק הבירה ל-Fe(SCN)2+
- כייל ספקטרופוטומטר גלוי באמצעות מים מזוקקים כריקים.
- הוסף 1.0 מ"ל של 1.0 × 10-4 M Fe(NO3)3 פתרון מבחנה.
- לאותה מבחנה, הוסף 5.0 מ"ל של פתרון KSCN 0.50 M.
- לאותה מבחנה, להוסיף 4.0 מ"ל של פתרון 0.10 M HNO3. מכסים את הצינור באצבע עם כפפות ומנערים בעדינות כדי לערבב.
- השתמש פיפטה פסטר להעביר כמות קטנה של הפתרון cuvette. ודא כי רמת הנוזל היא מעל הנתיב של קרן האור בספקטרופוטומטר.
- מניחים את הקובט בספקטרופוטומטר, כך שהאור עובר דרך הצדדים השקופים.
- רכש ספקטרום ורשום את הערךהמרבי של λ ואת הספיגה ב- λmax.
- על מנת לבנות עקומת חוק בירה, יש להכין ולמדוד פתרונות נוספים עם ריכוזים ידועים של Fe(SCN)2+. חזור על שלבים 2 – 7 באמצעות אמצעי האחסון של פתרונות Fe(NO3)3, KSCN ו- HNO3 בטבלה 2. הקפד להשתמש באותה cuvette עבור כל המדידות, שטיפה 3 פעמים עם מים מזוקקים בין כל מדגם.
- התווה את הספיגה הנמדדת לעומת הריכוזים של Fe(SCN)2+ בכל מבחנה ולקבוע את קו ההתאמה הטובה ביותר לנתונים. השיפוע של קו זה הוא ספיגת הטוחנת ואורך השביל הוא 1 ס"מ.
2. מדידת K למערכת הברזל (III) תיוצינאט
- הכן 4 מבחנות בינוניות המכילות את הנפחים המצוינים של 0.0025 M Fe(NO3)3, 0.0025 M KSCN ו- 0.10 M HNO3 פתרונות בטבלה 3.
- מכסים כל שפופרת באצבע ומנערים בעדינות כדי לערבב. אפשר להם לעמוד לפחות 10 דקות. תקופת מנוחה זו מבטיחה כי הפתרונות נמצאים בשיווי משקל כימי.
- השתמש פיפטה פסטר להעביר כמות קטנה של פתרון 6 ל cuvette. ודא כי רמת הנוזל היא מעל הנתיב של קרן האור בספקטרופוטומטר.
- לרכוש ספקטרום ולתעד את הספיגה ב λמקסימום.
- תגובות מרובות עם ריכוזים ראשוניים שונים של מגיבים ניתן ללמוד כדי להמחיש כי K אינו תלוי בריכוז. כדי לקבוע K עבור תנאים התחלתיים שונים, חזור על שלבים 3 ו- 4 עבור פתרונות 7 – 9.
| מספר צינור | נפח 1.0 x 10–4 M Fe(NO3)3 (מ"ל) |
נפח 0.50 M KSCN (מ"ל) |
נפח 0.10 מ' HNO3 (מ"ל) |
| 1 | 1.0 | 5.0 | 4.0 |
| 2 | 2.0 | 5.0 | 3.0 |
| 3 | 3.0 | 5.0 | 2.0 |
| 4 | 4.0 | 5.0 | 1.0 |
| 5 | 5.0 | 5.0 | 0.0 |
טבלה 2. נפחים מתאימים של Fe(NO3)3, KSCN ו- HNO3 פתרונות שיוצבו בצינורות 2 - 5.
| מספר צינור | נפח 0.0025 M Fe(NO3)3 (מ"ל) |
נפח 0.0025 M KSCN (מ"ל) |
נפח 0.10 מ' HNO3 (מ"ל) |
| 6 | 1.0 | 1.0 | 5.0 |
| 7 | 1.0 | 2.0 | 4.0 |
| 8 | 2.0 | 2.0 | 3.0 |
| 9 | 2.0 | 3.0 | 2.0 |
טבלה 3. נפחים מתאימים של 0.0025 M Fe(NO3)3, 0.0025 M KSCN ופתרונות HNO3 של 0.10 M.
Results
טבלה 4 מפרטת את נתוני הספיגה והריכוז לפתרונות 1 – 5. ריכוזים של Fe(SCN)2+ נקבעו מהריכוזים הראשוניים של Fe3+ תחת ההנחה שכל Fe3+ מומר ל- Fe(SCN)2 +. עודף גדול של SCN- שימש צינורות 1 - 5 כדי להבטיח כי הנחה זו נכונה.
הטוחנת [Fe(SCN)2+] והספיגה משורטטות באיור 2. הספיגות הנמדדות מסכימות היטב עם החוק של באר.
טבלה 5 מפרטת ספיגות נמדדות וערכי K מחושבים עבור צינורות 6 – 9. ערכי K נקבעו באמצעות שיטת הטבלה ICE. ריכוזי המגיבים הראשוניים התבססו על הטוחנות הידועות של Fe3+ ו- SCN- בפתרונות המגיבים ובנפח הכולל של התגובה (10 מ"ל). ריכוז שיווי המשקל של Fe(SCN)2+ נקבע על ידי חלוקת ספיגה נמדדת על ידי ספיגת הטוחנת של Fe(SCN)2 +. כי כל המוצר נוצר מתגובת 1:1 של Fe3+ ו SCN-, ריכוז שיווי המשקל של Fe(SCN)2+ מתאים לירידה בריכוז המגיבים. טבלה 6 מציגה את התהליך עבור מבחנה 6.
קבוע שיווי המשקל מחושב מהריכוזים בשורת שיווי המשקל. עבור מבחנה 6,

ערך K הממוצע היה 147 ± 11, הממחיש כי K הוא בערך קבוע על פני טווח הריכוזים שנחקרו.

איור 2. גרף קו של ספיגה לעומת ריכוז עבור Fe(SCN)2+.
| צינור | [Fe(SCN)2+] (מול/ל) | ספיגה |
| 1 | 1.00 x 10–5 | 0.10 |
| 2 | 2.00 x 10–5 | 0.20 |
| 3 | 3.00 x 10–5 | 0.25 |
| 4 | 4.00 x 10–5 | 0.32 |
| 5 | 5.00 x 10–5 | 0.42 |
טבלה 4. ספיגה לעומת נתוני ריכוז עבור Fe(SCN)2+.
| צינור | ספיגה | K |
| 6 | 0.120 | 136 |
| 7 | 0.268 | 161 |
| 8 | 0.461 | 142 |
| 9 | 0.695 | 150 |
שולחן 5. ערכי ספיגה נמדדים ו- K מחושב לתגובת ברזל (III) עם תיוציאנט.
| [Fe3+] (מול/ל) | [SCN–] (מול/ל) | [Fe(SCN)2+] (מול/ל) | |
| הראשונית | 3.57 x 10–4 | 3.57 x 10–4 | 0 |
| שינוי | –1.58 x 10–5 | –1.58 x 10–5 | +1.58 x 10–5 |
| שיווי משקל | 3.41 x 10–4 | 3.41 x 10–4 | 1.58 x 10–5 |
שולחן 6. טבלת ICE הממחישה את התהליך המשמש עבור מבחנה 6.
Application and Summary
קבוע שיווי המשקל מספק מידע שימושי על המידה שבה תגובה תמשיך ליצור מוצרים לאורך זמן. תגובות עם ערך גדול של K,גדול בהרבה מ-1, ייצרו מוצרים שכמעט הושלמו בהינתן מספיק זמן(איור 3). תגובות עם ערך של K פחות מ- 1 לא ימשיכו קדימה במידה משמעותית. קבוע שיווי המשקל משמש אפוא כמדד של היתכנות של תגובה כימית.

איור 3. קבוע שיווי המשקל של תגובה זו גדול מ- 1. כמות משמעותית של צורות מוצר צבעוניות בכל מקרה, למרות הריכוזים הראשוניים של מגיבים שונים.
קבוע שיווי המשקל מספק גם מידע תרמודינמי שימושי על השינויים באנרגיה חופשית, אנטלפיה ואנטרופיה במהלך תגובה כימית. קבוע שיווי המשקל קשור לשינוי האנרגיה החופשית של התגובה:
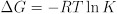
שינוי האנרגיה החופשית של התגובה קשור בתורו לשינויי האנטלפיה והאנטרופיה של התגובה:
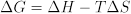
מדידות של תלות הטמפרטורה של K יכול לחשוף את שינוי האנטלפיה ΔH ואת האנטרופיה לשנות ΔS לתגובה. בנוסף לספק כימאים עם תובנה על דפוסים בהתנהגות מולקולרית, טבלאות של נתונים תרמודינמיים ניתן להשתמש כדי לזהות תגובות עם תכונות תרמודינמיות חיוביות. לדוגמה, תגובות redox המשחררות כמויות גדולות של אנרגיה (הקשורות לערכי ΔG שליליים) הן מועמדות אטרקטיביות לסוללות.
ערכים של K עבור תגובות דיסוציאציה חומצה (Kערכים) שימושיים לחיזוי התוצאות של תגובות בסיס חומצה, אשר נשלטים תרמודינמית. חומצות חזקות קשורותלערכי Kגדולים וחומצות חלשות עםערכי Kקטנים. מחווני pH הם חומצות חלשות עם צורות חומציות בסיסיות וצבעוניות שונות, וה- pKa (הלוגריתם השלילי של Ka) של מחוון מייצג את ה- pH שבו מתרחש שינוי צבע כחומצה או בסיס נוסף לפתרון המחוון.
באופן דומה, Ka ערכים משמשים להכנת פתרונות מאגר כדי להשיג ערך pH היעד. ה- pKa של חומצה חלשה מייצג את החומציות שבה החומצה והבסיס המ מצומד שלה נמצאים בתמיסה בריכוזים שווים. כאשר כמויות שוות של חומצה חלשה ובסיסה מצומד מומסים בתמיסה, ה- pH של הפתרון שווה ל- pKa של החומצה החלשה.
Skip to...
Videos from this collection:

Now Playing
קביעת ספקטרופוטומטריה של קבוע שיווי משקל
General Chemistry
158.3K Views

כלי זכוכית ושימושים נפוצים במעבדה
General Chemistry
654.7K Views

פתרונות וריכוזים
General Chemistry
273.3K Views

קביעת הצפיפות של מוצק ונוזל
General Chemistry
555.1K Views

קביעת הרכב אחוז המסה בפתרון מימי
General Chemistry
383.1K Views

קביעת הנוסחה האמפירית
General Chemistry
180.4K Views

קביעת כללי המסיסות של תרכובות יוניות
General Chemistry
141.1K Views

שימוש במד pH
General Chemistry
344.6K Views

מבוא לתמצית
General Chemistry
423.6K Views

חוק הגז האידיאלי
General Chemistry
78.2K Views

עקרון לה שאטלייה
General Chemistry
264.6K Views

דיכאון נקודת הקפאה כדי לקבוע תרכובת לא ידועה
General Chemistry
160.6K Views

קביעת חוקי התעריפים וסדר התגובה
General Chemistry
195.8K Views

שימוש בסריקה דיפרנציאלית קלורימטריה למדידת שינויים באנטלפיה
General Chemistry
44.4K Views

מתחמי כימיה של תיאום
General Chemistry
91.2K Views
Copyright © 2025 MyJoVE Corporation. All rights reserved