Evaluating the Heat Transfer of a Spin-and-Chill
Overview
Source: Michael G. Benton and Kerry M. Dooley, Department of Chemical Engineering, Louisiana State University, Baton Rouge, LA
The Spin-and-Chill uses heat transfer and fluid flow fundamentals to chill beverages from room temperature to 38 °F in as little as 2 min. It would take a refrigerator approximately 240 min and an ice chest approximately 40 min to achieve an equivalent temperature change. This is accomplished Spin and Chill by spinning a can or bottle at up to 500 rpm, which creates little or no foaming.
In this experiment, the efficacy of spinning a cylinder (i.e., soda can) at high speeds to cool a soft drink will be evaluated. Operational parameters, such as rpm and spin time, will be varied to assess their effect on heat transfer, and the heat transfer coefficient will be calculated using a lumped parameter model.
Principles
The Spin-and-Chill makes use of convective heat transfer. By spinning the can in contact with an external ice bath, warm liquid from the middle of the can moves to the outside and comes in contact with the colder surface. Then, energy is transferred from the warm liquid to the cold surface in the form of heat. This continues until the entire vessel has been cooled. Refrigeration makes use of a similar process1. In refrigeration, refrigerant cycles through the system, and undergoes a reduction in pressure1. In response, the temperature of the refrigerant decreases greatly to a temperature below the temperature of the space being cooled1. This temperature difference results in heat moving naturally from the warmer space to the cooler refrigerant, where it is taken in, later emitted, and the process repeats itself1.
The Spin-and-Chill is analogous to the cooling of a batch vessel and somewhat analogous to the cooling of a fluid flowing in a pipe. For fluid in an agitated vessel or in a pipe, the average fluid velocity is known. Theory and correlations are available to predict heat transfer coefficient (h) values. Because the cans in the Spin-and-Chill are rotating at very fast speeds (up to 500 rpm) the contents of the cans can be considered well-mixed. This means the temperature within the can will be uniform with respect to position, although the liquid in the can will be chilling as the can spins. This uniform temperature means conduction is negligible within the can and the heat flow in the Spin-and-Chill is primarily controlled by resistances to convection.
Because conduction within the can is negligible and convection is the determinant factor in cooling the can's contents, lumped parameter analysis can be used to model the cooling behavior. The lumped parameter analysis reduces a thermal system to a single discrete "lumped resistance", where the temperature difference of each individual resistance is considered unknown. The following equation is used in lumped parameter analysis:

In this equation, T(t) is the temperature of the can at time t, T∞ is the temperature in the bulk phase outside the can (ice), T(i) is the initial temperature in the can, h is the lumped heat transfer coefficient, A is area, t is run time, ρ is an average density, Cp is the average heat capacity, and V is volume. Recall the liquid inside and outside the can are assumed to have bulk temperatures that are uniform with respect to position. However, the temperature of the can is still dropping during the cooling process. The temperature of the ice bath is essentially constant (0 °C) because the bath is infinite compared to the volume of the can.
Heat flow from the water in the can to the ice involves an internal resistance, a wall resistance, and an external resistance (Figure 1). In the Spin-and-Chill, both the water in the can and the ice are well mixed, simplifying the system to a one-dimensional heat transfer problem.

Figure 1: A schematic of temperature conditions for the Spin-and-Chill.
In this case, the wall is very thin and the wall resistance can be neglected. Figure 2 shows the evolution of the internal temperature profiles with respect to time.

Figure 2: A schematic of temperature conditions in the can (hot fluid) over time. During spinning, convective heat transfer causes the temperature of the fluid in the can to decrease.
When using an ice chest, the liquid in the can will be moving even without mixing or spinning. Natural convection will occur due to the temperature gradients.
Procedure
1. Testing the Spin-and-Chill
- Fill the aluminum soda can with room temperature water and then record the temperature.
- Measure the total weight of the ice being used with the balance, enough to surround the Spin-and-Chill.
- Seal the aluminum soda can using a plastic sealing lid and insert the assembly into the Spin-and-Chill.
- Activate the Spin-and-Chill. It should run about 2 min at ~ 300 rpm.
- Remove the aluminum soda can from the Spin-and-Chill and remove the plastic sealing lid. Record the final temperature of the water within the aluminum soda can.
- Record the amount of ice that melted using either a graduated cylinder or a balance.
2. Lumped Parameter Model
- Starting with the can at room temperature, perform ~ 4 single runs using the Spin-and-Chill. Each should run last ~ 2 min at a constant rpm (e.g., 500).
- Record the final temperature of the water within the can after each run.
- Then, run the Spin-and-Chill sequentially three times starting with a warm can. Perform a reasonable number of replicates for the sequential Spin-and-Chill experiment. It should run for ~ 2 min at a constant rpm (e.g., 500).
- Record the amount of ice melted and final temperature after each run. Be careful when you open the can - it may or may not foam if a carbonated beverage is used.
- Repeat as desired to test the effect of Spin-and-Chill parameters. For example, vary the operating rpm at constant spin times or vary the spin times at constant rpm.
Results
The lumped parameter model is used to determine the heat transfer coefficient, h, for the different experimental conditions. To calculate the efficiency, we first determine the energy transferred as heat into the ice bath from the liquid in the can. If the system were adiabatic (100% efficient), Qwater + Qice = 0. The efficiency is determined by dividing the absolute value of heat released by the water in the can (Qwater) by the heat absorbed by the ice during melting (Qice). The observed efficiency is not dependent on any limiting case or heat transfer mechanism.
Results for ten two-minute runs at 300 rpm were averaged (Table 1). The water in the can was cooled by an average of 26.2 °F after the two minute spin. The average efficiency,η, was 77.7%.
| Trial # | Initial T (°F) | Final T (°F) | ΔT (°F) | Ice Δm (lbs.) | Qice | Qwater | η | h (Btu/hr-ft2-F) |
h (W/m2-C) |
| 1 | 77 | 53.4 | 23.6 | 0.172 | 24.8 | 18.5 | 74.5 | 70.5 | 401 |
| 2 | 84.7 | 60.1 | 24.7 | 0.17 | 24.5 | 19.3 | 78.9 | 59.9 | 340 |
| 3 | 86 | 59.7 | 26.3 | 0.175 | 25.2 | 20.6 | 81.7 | 63.4 | 360 |
| 4 | 83.1 | 55.4 | 27.7 | 0.195 | 28.1 | 21.7 | 77.3 | 74.3 | 422 |
| 6 | 81.9 | 52.3 | 29.5 | 0.212 | 30.5 | 23.1 | 75.7 | 85.2 | 484 |
| 7 | 83.7 | 58.3 | 25.4 | 0.171 | 24.6 | 19.9 | 80.7 | 64.2 | 365 |
| 8 | 79.2 | 50.7 | 28.4 | 0.203 | 29.2 | 22.3 | 76.2 | 87.8 | 499 |
| 9 | 81.7 | 56.3 | 25.4 | 0.181 | 26.1 | 19.9 | 76.2 | 68.0 | 386 |
| 10 | 81.9 | 56.7 | 25.2 | 0.173 | 24.9 | 19.7 | 79.2 | 66.9 | 380 |
| Avg. | 82.1 | 55.9 | 26.2 | 0.18 | 26.4 | 20.6 | 77.7 | 70.5 | 400 |
Table 1: Single-run nominal temperature change from 82 F to 56 F. Water in can: 0.783 lbs
Using three sequential 2-min runs at a constant rpm, it was observed that cooling performance was enhanced with longer run times (Figure 3) Reducing spin time led to a higher average temperature.

Figure 3: Temperature drop as a function of spin time. As spin time at a constant rpm increases, the observed temperature drop (Tfinal- Tinitial) also increases. Water in can: 0.783 lbs.
For the sequential runs, the efficiency, η, decreased from 78% to 71% and then to 50% over the course of the three runs (Figure 4). This decrease in efficiency is common in heat transfer when the temperature differential driving the heat transfer become smaller.

Figure 4: Efficiency decreases in sequential runs. The error bars represent standard deviation of at least three replicates. Water in can: 0.783 lbs rpm: ~300.
When varying the rpm, it was found that the average temperature of the liquid inside the can was inversely proportional to the rpm (Figure 5). Higher rpm led to lower liquid temperatures, closer to the ideal temperature, whereas lower rpm led to higher average temperatures.
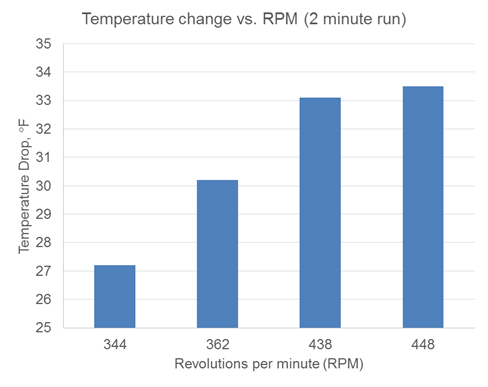
Figure 5: Temperature drop as a function of rpm. As rpm increases, the observed temperature drop (Tfinal- Tinitial) also increases. Water in can: 0.783 lbs
Application and Summary
This experiment is designed to assess the ability of the Spin-and-Chill to cool a soft drink at record speeds. The lumped parameter model was used since convection was much more important than conduction (due to the high rate of mixing).
The data collected calls into question the ability of the Spin-and-Chill to cool at warm can of soda to 38 °F in 2 minutes. However, with three sequential uses and a time period of about 6 minutes, the Spin-and-Chill can cool the soft drink to the desired temperature of 38 °F, still a major improvement over ice chests or household refrigerators. While the initial claims were invalidated, the concept does provide an advanced cooling method that could be made more efficient with more testing in the future.
The lumped parameter model has been applied to a wide variety of fields. By use of a lumped parameter analysis, forensics labs can determine time of death of a human body2. Forensic scientists treat the body as a lumped system2. Previous research was conducted on cooling when considering factors such as body size and shape2. Differential equations are then used with these known cooling factors to determine relative time of death2.
Another use of the lumped parameter model is in the advancement of HVAC (heating, ventilation, and air conditioning) systems3. Heat load distribution can be computationally predicted with a lumped parameter model to maximize energy efficiency3. These models account for fluid transport, energy transport, thermodynamics, and psychrometrics3. By fitting HVAC systems to a lumped model, engineers can maximize their efficiency, reducing costs and energy usage, while increasing the effectiveness of the climate control system3.
Modeling of convection is important in a variety of engineering fields, including materials processing, power station engineering, and refrigeration. Heat exchangers are one common application of convective heat transfer modeling4. These devices take energy from a hot stream and use it to heat a cooler one4. Shell and tube are the most common type of exchangers4. They are normally long cylinders, similar to the model used for this experiment, but much larger in scale4. Several tubes inside a larger cylindrical shell contain one flowing liquid, while a separate one flows through the shell4. Flow can be in the same or different directions. Heat will flow from the hottest stream to the colder one4. These tools can be used in many industries, such as chemical manufacturing and oil refining, where they can be used to heat or cool chemicals or oil4.
References
- Vapor-compression Refrigeration." ChemEngineering - Vapor-compression Refrigeration. N.p., n.d. Web. 01 Dec. 2016.
- Bartgis, Catherine, Alexander M. Lebrun, Rhongui Ma, and Liang Zhu. "Determination of Time of Death in Forensic Science via a 3-D Whole Body Heat Transfer Model." Journal of Thermal Biology (2016). Web.
- Wemhoff, A.p., and M.v. Frank. "Predictions of Energy Savings in HVAC Systems by Lumped Models." Energy and Buildings 42.10 (2010): 1807-814. Web.
- Encyclopedia of Chemical Engineering Equipment." Heat Exchangers - Heat Transfer - MEL Equipment Encyclopedia 4.0. N.p., n.d. Web. 01 Dec. 2016.
Skip to...
Videos from this collection:

Now Playing
Evaluating the Heat Transfer of a Spin-and-Chill
Chemical Engineering
7.4K Views

Testing the Heat Transfer Efficiency of a Finned-tube Heat Exchanger
Chemical Engineering
17.9K Views

Using a Tray Dryer to Investigate Convective and Conductive Heat Transfer
Chemical Engineering
43.9K Views

Viscosity of Propylene Glycol Solutions
Chemical Engineering
32.8K Views

Porosimetry of a Silica Alumina Powder
Chemical Engineering
9.6K Views

Demonstration of the Power Law Model Through Extrusion
Chemical Engineering
10.0K Views

Gas Absorber
Chemical Engineering
36.7K Views

Vapor-liquid Equilibrium
Chemical Engineering
88.9K Views

The Effect of Reflux Ratio on Tray Distillation Efficiency
Chemical Engineering
77.7K Views

Efficiency of Liquid-liquid Extraction
Chemical Engineering
48.5K Views

Liquid Phase Reactor: Sucrose Inversion
Chemical Engineering
9.7K Views

Crystallization of Salicylic Acid via Chemical Modification
Chemical Engineering
24.2K Views

Single and Two-phase Flow in a Packed Bed Reactor
Chemical Engineering
18.9K Views

Kinetics of Addition Polymerization to Polydimethylsiloxane
Chemical Engineering
16.1K Views

Catalytic Reactor: Hydrogenation of Ethylene
Chemical Engineering
30.4K Views
Copyright © 2025 MyJoVE Corporation. All rights reserved