간섭 및 회절

파도는 공간 및 / 또는 시간에 일부 물리적 수량의 진폭에 진동이다. 파도 또는 파도의 다른 부분은 중첩하고 "간섭"하여 번갈아 강하고 약한 진폭을 생성 할 수 있습니다. 간섭은 파도와 관련된 가장 특징적인 현상 중 하나입니다. 한 차원 선(x 축)을 따라 전파되고 수학적으로 표현되는 두 파도의 간단한 예를 고려하십시오.

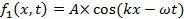
그리고

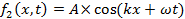
각각 오른쪽(+x 방향)과 왼쪽(−x 방향)으로 전파합니다. 여기서, A는 피크 진폭이며, k는 "웨이브 넘버" 또는 "웨이브 벡터"로 정의되고,

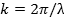
여기서 λ는 파장(파장의 공간 주기)입니다. ω은

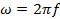
여기서 f는 주파수이며,

여기서 T는 파도의 기간(시간)입니다. 두 파도가 겹치면 진폭이 합산됩니다("파도의 중첩 원리"라고 함).

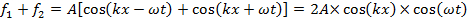
이는 "서있는 파도"라고도합니다. 그 위치에서,

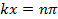
(n은 정수인) 및,

진동 (시간 t의함수로) 최대 진폭 (-2A와 +2A 사이)가있을 것입니다. 대조적으로, 위치,

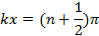
그리고

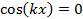
진동은 0(따라서 최소) 진폭("노드"라고도 함)을 갖습니다. 강하고 약한 파진환의 이러한 공간 적 변화는 "간섭 패턴"을 나타냅니다. 이 현상은 2차원 및 3차원 공간에서 파도에 일반화될 수 있다. 또한 이 실험에서 관찰되는 단일 슬릿 회절 및 이중 슬릿 간섭(전자파)의 현상의 근간을 형성한다.

파장(λ)의 빛이 폭(a)의 좁은 슬릿에 비추면(도 1a에서괄호로 표시됨), 슬릿으로부터 멀리 떨어진 광 강도(파도의 피크 진폭의 제곱에 비례)는 폭방향("y-axis")을 따라 크고 작은(거의 0) 값으로 번갈아 가며 빛의 "회절 패턴"(작은 조리개를 통해)으로 알려진 이러한 교대는 파도의 특징적인 현상이기도 합니다. 근본적으로, 조리개 후 광파의 다른 부분 사이의 간섭에서 발생합니다 (특히, 조리개의 두 모서리 사이의 점은 다른 방향으로 빛의 파를 "다시 방출"합니다). 광 강도의 각도 변형은 I(θ)로 표시되며, 여기서 θ는 방향의 각도(+y 또는 -y쪽으로) "직선 통과" 방향에서 y = 도 1a에서0을 통해 멀리 떨어진 방향으로 나타낸다. 작은 θ의 경우, I(θ)가 |신(πaθ/λ)/(πaθ/λ)|2에 약 비례한다는 것을 보여줄 수 있다. 즉, "어두운"에 대한,

그리고 "밝은,

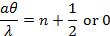
. 화면이 슬릿에서 거리 L에 배치되면 그림 1b (왼쪽)에 스키마하게 표시된 것처럼 y의 다른 위치에서 밝고 어두운 프린지가 번갈아 가며 관찰됩니다. 작은 θ의 경우(중심 y = 0에 가깝음),

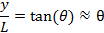
따라서 프린지 강도는 대략로 설명될 수 있고,

(이 함수는 그림 1b,오른쪽에 괄호로 표시됩니다). 센터 y = 0은 항상 밝은 프린지(죄(t)/t는 t→0일 때 최대 1을 가지며 t가 0에서 π 증가로 단조로 아래로 감소하기 때문에). 중심에서 벗어나 "첫 번째 순서"어두운 프린지가 중심을 이겨,

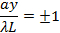
그런 다음 밝은 프린지를 중심으로,

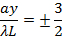
그런 다음 다시 어두운 프린지를 중심으로,

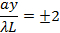
그런 다음 다시 중심의 밝은 프린지,

등등. 중앙 외부의 각 밝은 프린지의 폭은 약 λL/a이며, 중앙 밝은 프린지는 두 배 너비 (너비 ~ 2λL /a, 또는 ± λL/a에서 두 개의 1 차 어두운 프린지 사이의 분리). 슬릿이 좁거나 파장 λ 또는 화면 거리 L이클수록 프린지가 더 확산됩니다.

도 1과유사한 설정에서 분리 D(그림 2a에묘사됨)로 두 개의 밀접하게 분리된 좁은 슬릿을 통해 빛이 비추면 유명한 "영의 이중 슬릿 간섭 패턴"을 관찰할 수 있다(도 2b에괄전형으로 표시됨). 작은 θ(중심 y =0에 가깝음)의 경우, 밝은 프린지를 중심으로,

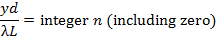
그리고 어두운 프린지를 중심으로,

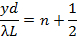
관찰할 수 있습니다. 위에서 설명한 단일 슬릿 회절 패턴과는 달리, 여기에 모든 라이트 프린지(y = 0의 중앙 프린지 포함)는동일한 너비를 가지며 λ L/d에 의해 동등하게 간격을 두고 있습니다. 좁은 슬릿은 여전히 회절 패턴을 생성하지만, 일반적으로 슬릿 폭(a)은분리(d)보다훨씬 작으며 강도 변조(회절 패턴으로 인해)는 훨씬 더 가깝고 동등하게 간격이 있는 이중 슬릿 간섭 프린지에 겹쳐진다.

상기 논의의 광원은 완벽하게 단색(잘 정의된 파장 λ을 의미함)과 일관성(파도 진동이 한 위치에서 최대 또는 최소에 도달하는 것을 의미하는 경우, 다른 위치에서 최대 또는 최소에 도달할 것이라는 순간을 예측할 수 있음)로 가정한다. 예를 들어, 파도가 코신 함수에 의해 cos(kx−ωt+φ)로 묘사되는 경우, 일정한 위상 φ, 이는 시작점을 재정의하여 0으로 선택할 수 있다. 레이저는 이상적인 광원의이 종류에 대 한 최고의 근사치 이기 때문에, 레이저 빔이 실험에서 광원으로 사용 됩니다 (역사적으로 사전 레이저 시간에, 이러한 실험은 작은 구멍 비록 빛을 통과 하 여 생산 하는 것과 같은 포인트 같은 광원을 사용 하 여).

실제 회절 및 간섭 프린지(프린지의 모양과 강도 포함)는 광원과 슬릿의 결함으로 인해 이러한 가장 간단한 경우및 근사치에서 위에서 설명한 것보다 더 복잡하고 덜 "이상적"으로 보일 수 있음을 주목하는 것이 중요합니다. 예를 들어, 광원이 덜 일관된 경우 변두리의 대비를 줄일 수 있습니다(예: "어두운" 프린지가 실제로 0 강도에 도달하지 않음). 한편, 프린지의 위치와 간격은 일반적으로 위에서 설명한 간단한 모델에 의해 잘 예측됩니다.
 

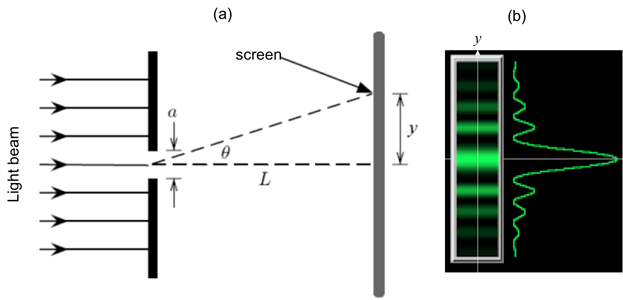
그림 1: 단일 슬릿 회절. (a)광학 설정의 회로도, 폭의 좁은 슬릿을 통해 빛나는 빛, 및 관측 화면 위치 거리 L; 및(b)중심에서 멀리 떨어진 수직 거리(y)의 함수로서 화면에서 관찰될 수 있는 회로도 회절 프린지 패턴(왼쪽) 및 해당 광 강도 변화.

 
그림 2: 이중 슬릿 간섭. (a)광학 설정의 회로도, 거리 D로 분리된 두 개의 좁은 슬릿을 통해 빛이 비추고, 관측화면은 거리 L거리에 위치한; 및(b)화면에서 관찰될 수 있는 회로도 간섭 프린지(동등하게 간격).

2.3단계의 경우, 벽에서 관찰될 수 있는 대표적인 라이트 패턴이 도 3b로나타내며, 특징적인 회절 프린지를 나타낸다. 중앙 밝은 프린지는 다른 밝은 프린지 (너비가 거의 동일함)와 거의 두 배 넓으며 밝은 프린지의 오버 강도는 단일 슬릿 회절 패턴에 예상대로 y축을 따라 중심에서 떨어져 부패합니다.

3.3단계의 경우, 벽에서 관찰될 수 있는 대표적인 라이트 패턴이 도 4b에도시된다. 2.3 단계에서 관찰된 회절 패턴과 유사한 전체 강도 변조 패턴이 있다. 이것은 실제로 좁은 슬릿의 각각에 기인하는 회절 패턴입니다. 회절 패턴의 밝은 영역 내에서, 하나는 대략 동등하게 간격밝은 줄무늬를 관찰 할 수 있습니다. 이중 슬릿 간섭 프린지입니다. 이러한 간섭 프린지는 슬릿 분리 d가 슬릿 너비보다 훨씬 크기 때문에 회절 패턴의 밝은 영역보다 훨씬 좁습니다(이러한 길이의 상호는 간섭 또는 회절 프린지의 폭을 각각 제어합니다).

그림 3. 다이어그램 표시:(a)열린 구멍이 있는 판지상에 고정된 알루미늄 호일에 단일 슬릿에 빛나는 레이저 빔; 및(b)슬릿 후 화면에서 관찰된 대표적인 회절 프린지.

그림 4. 다이어그램 표시:(a)열린 구멍이 있는 판지상에 고정되는 알루미늄 호일에 이중 슬릿에 빛나는 레이저 빔; 및(b)이중 슬릿 후 화면에서 관찰된 대표적인 간섭 프린지.

이 실험에서, 우리는 레이저 빔을 사용하여, 빛의 단일 슬릿 회절 패턴과 이중 슬릿 간섭 패턴을 시연했다. 이러한 특징적인 파도 현상을 관찰하는 것은 빛의 파성질을 보여줍니다.

빛의 회절과 간섭은 빛이 전자파임을 확립하는 데 도움을 주면서 광학 개발에 필수적인 역할을 했습니다. 이러한 효과는 광학 및 포토닉스를 기반으로 하는 많은 기술에서도 중요합니다. 예를 들어, 회절은 일반적으로 작은 물체 또는 작은 구멍의 크기를 측정하는 데 사용되며 광학 현미경 및 이미징 시스템을 설계할 때 고려해야 할 중요한 측면이기도 합니다. 광학 간섭(소위 "간섭"이라고 함)의 측정은 거리(예: 광원 또는 거울 사이)의 정밀 측정에 사용될 수 있으며 가공, 지질학 및 천문학(예: 중력파를 감지한 LIGO 프로젝트에서)에 이르는 응용 제품을 발견했습니다.

실험의 저자는 게리 허드슨의 재료 준비에 대한 도움을 인정하고 비디오의 단계를 시연하기위한 Chuanhsun 리.