定在波
概要
ソース:アリアナ ブラウンAsantha Cooray 博士は、物理学教室 & 天文学、物理的な科学の学校、カリフォルニア大学、アーバイン、カリフォルニア州
定在波、または停滞性波動が伝播していないように見える、反対方向に同じ周波数と振幅の 2 つの波の干渉によって生成される波。これらの波はない直線的な動きで上下に振動する表示され、マンドリン ギターの弦、湖の水や部屋の空気のような有限のメディアを振動に最も簡単に識別されます。たとえば、文字列は両端固定、長さに沿って旅行 2 つの同じ波が送信される場合、最初の波が終わりバリアにヒットし、反対の方向に反射し、2 つの波が定在波を生成する superpose。この動きは、媒体の長さによって定義される周波数と周期、単振動する運動の視覚的な例です。簡単な調和運動は振動、定期的な運動、意味遠い何かを押すと、一生懸命それを押し戻す復元力は、変位に比例します。
この実験の目的は、波の重ね合わせと定在波を作成する反射の役割を理解し、最初のいくつかの共振周波数の計算にこれらの概念を悪用または高調波、定在波セクシーに。オブジェクトを生成する各周波数が独自の定在波のパターン、最も低い可能な周波数の波が基本周波数と呼びます。調和は、整数番号で基本周波数に比例周波数を持つ波です。
原則
2 つの波は同時にパス内の同じポイントに到着、彼らは干渉します。結果として得られる波の振幅は 2 つの線形波 (直線波の重ね合わせの原理の直接結果) の振幅値の総和です。これらの 2 つの波は互いのパスまたは速度を変更することがなくお互いを通過します。建設的な干渉段階で届く波の振幅を追加するとき、に発生します。会うときに波の位相、振幅を引くし、破壊的な干渉を受けます。同じ振幅の 2 つの波は、破壊的な干渉を受けること、その振幅は (図 1) をキャンセルします。
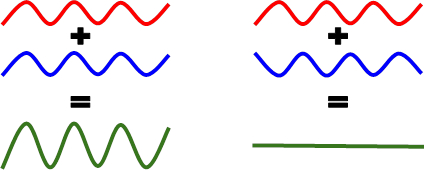
図 1:等しい振幅を持つ 2 つの波。左: 建設的な干渉。右: 破壊的な干渉。
進行波境界 (すなわち、別の媒体) に達する、そのエネルギーの一部が反映されます、いくつかは新しい媒体に転送され、一部が吸収されます。完璧な反射波シナリオでは、すべてのエネルギーが反映されて、システムに供給する必要がないので外のエネルギー、エネルギーは保存されています。固定境界条件で、有限の文字列のような媒体の波の最後の境界で反射され 180 ° 位相シフトを経験します。境界の間を行ったり来たり波は干渉し、定在波(図 2).として知られている静止パターンを作成するこのプロセスが時間の長時間にわたって続く場合最小振幅 (ノード) のポイントは、互いに相殺波を逆位相があるポイントです。最大振幅 (antinodes) のポイントはポイントで波がある同相、そのそれぞれの振幅を兼ね備えています。

図 2:長さ 2λ 培地での定在波。これはまた第 4 高調波の視覚的表現です。
最も単純な定在波は、基本周波数とも呼ばは、 Lの文字列の長さは ½λ、波長 λ であるときに発生します。これはですね

だから点固定文字列に最初の振動は動きで縄跳びのプロファイルに似ています。次の可能な定在波をするためには、ノードを追加する、センターで、 Lが λ と同等になります: 結果は短い波長の定在波パターン。基本周波数よりも短い波長の定在波パターンは、高調波と呼びます。ノードの追加を続けて、私たちを見つけます。
 (関係式 1)
(関係式 1)
nはノードと生成された高調波の数はn番目の調和として時々 呼ばれます。(注: 一部は他はnを参照してください最初高調波と基本周波数を参照してください最初の高調波として 2 次高調波を =)。
伝搬波エネルギーが波と一緒に転送されます。1 つのセクションが上方に移動すると、変位を移動次のセクションに力を発揮します。つまり、作業が行われます。定在波内のノードのような変位を経験ポイントを行うことはできません、隣接するセクションで動作します。したがって、文字列上のノード間でのエネルギーは送信されず、定在波のエネルギーを伝達しません。代わりに、定在波のエネルギーを弾性ポテンシャル エネルギー波が彼らの最大振幅で一瞬静止文字列が振動し、グリセリンに粒子の真ん中にフラットの場合、運動エネルギーは速度方向と交互に。さらに、定在波の動きを受けているひもの部分にある粒子を検討してください。定在波は、単純な前後運動、ので、周期を測定可能で、前後に移動するこの粒子が表示されます。定在波でこの振動と弾性体とポテンシャル エネルギーの関係は簡単な調和運動としてを説明し、周波数f周期Tの観察可能な性質を有しています。定在波では、頻度は, 単位時間あたりの振動数サイクル期間はいずれかのサイクルを完了するために必要な時間と、定義または。
 (式 2)
(式 2)
この演習ではこれらすべてのプロパティをさまざまな波とセクシーなによる定在波を作成することによって探る。
手順
1. 重ね合わせとセクシーなパルスの反射を観察すること
- またがってスリンキーや鋼春縦床や廊下、一方の端を保持している 1 人の学生と他を保持別の学生。テープを使用して、2 つ縦 'の障壁、スリンキーの真ん中から足についてそれぞれの側をマークします。各側面の中間から 2 フィート障壁を繰り返します。
- 交代でマークされた障壁内にとどまる振幅パルス (セクシーな小さな距離水平およびすぐにはスタート地点に戻ってスナップけいれん) を起動します。
- 次に、両端から同時に同じ極性の異なるパルスを起動してみてください、パルスに会うときに何が起こるかに注意してください。重畳波必要があります振幅の 2 倍、最初録音された障壁を横断し、2 番目のテープのバリアを打った。
- 同一パルスを立ち上げるが、反対の極性と同時にパルスつれを観察し、。パルスとスーパーイン ポーズ、旅行、障壁に触れて、進み互いを取り消すべきです。
- 位置にしっかりと保持することによって、スリンキーの一端を修正します。固定位置の下に 1 つのパルスを送信し、時の反射波の振幅を確認します。それが反対の極性に戻って反映されます。
2. 春の定在波の周波数を測定
- 客室や廊下、メジャー、レコード長で、セクシーなストレッチします。
- 一端動き (強く抱きしめて) から優しく固定基本周波数の定在波を見つけるまで一貫性のある動きで水平方向にもう一方の端をスライドを開始します。この高調波の動きで縄跳びのプロファイルのような前後移動 1 つの振幅のみ 1 つの波頭があるはずです。ストップウォッチを使用すると、いくつかの波のサイクルにかかる時間を記録します。1 つの完全なサイクルは起動時、片側にグリセリン フォームは、他の側に、グリセリンを形成する中心を通ってスライドし、元の位置に戻ります。これらの測定値を使用すると、頻度、期間、および方程式の 1 と 2を使用してこの波の波長を計算します。
- 次高調波までスライドの最後の速度を上げる (n = 2) を実現します。この高調波の反対の方向で動く、反対側の 2 つの波頭とする必要があり、2D プロジェクションの手紙のように見えますが「回転。周波数を測定し、期間とこの波の波長を計算します。この頻度は、基本周波数の比率は何ですか。
- 次の高調波について前の手順を繰り返します (n = 3)。
結果
| 高調波 (n) | # サイクル | 合計時間 (秒) | 周波数 (Hz) | f/f0 | 期間 (秒) | 波長 (m) |
| 1 | 10 | 19.2 | 0.521 (f0) | 1 | 1.210 | 16 m |
| 2 | 10 | 9.75 | 1.026 | 1.97 | 0.975 | 8 m |
| 3 | 10 | 6.21 | 1.601 | 3.07 | 0.625 | 5.33 m |
表 1:セクション 2 - 伸縮ばね長さ 8 m を =
セクション 1 の有限媒質中の反射波の重ね合わせの原則は実証、パルスに送られた、スリンキーの長さとして確認されました。具体的には、同一の振幅と位相の 2 つの波を満たして、建設的な干渉を受けるし、その振幅を追加するを参照してください。同様に、我々 は反対の極性 (180 ° 位相シフト) と同じ振幅の 2 つの波を満たして、破壊的な干渉を受けるし、その振幅をキャンセルを参照してください。これらの原則の後者は、定在波パターンを理解する鍵です。
セクション 2 のノードと、セクシーなの antinodes は、簡単に様々 な周波数で表示されていた。ノードの数が増えるにつれて頻度もそうです。波長の減少は当然のことながら、波長は周波数に反比例します。高調波の周波数は、正の整数nに対応する基本周波数の倍数。たとえば、 nを使用して = 2 高調波、頻度測定、単位時間あたりのサイクル数として定義されています。
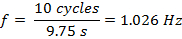
期間頻度 (式 2) の逆数として定義と等しい。
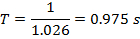
波長は、方程式 1として定義されます。

最後に、我々 は計算することで高調波と基本周波数の整数比例関係を見ることができます。
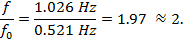
申請書と概要
この実験では 2 つのデモンストレーションの波の重ね合わせと定在波の概念を検討しました。波の反射と破壊的な干渉と建設的な最初のデモンストレーションで可視化しました。第二に、周波数と周期の変化を測定したし、高い高調波周波数は整数に発見された基本的な周波数の倍数。
現実の世界での定在波の有名な例は、ギター、または任意の弦楽器の文字列です。撥弦が特定の周波数を発するこれらの楽器はどのようにピンと張ったと密な文字列によって、文字列の長さ。各文字列はのみだけ特定の定在波や高調波、その文字列上に形成できるため特定のノートを作る。ミュージシャンは、自分の指を使用して、新しいノードを作成して、基本周波数に比例して高調波の新しいセットは文字列の長さを短くできます。適切な頻度で振動は言う指フレット上に文字列を固定はその文字列の長さで定在波を可能にする、奇妙な音、最終的に自分自身を相殺します。
定在波も自然湖と港のような境界水域で頻繁に発生します。時に、彼らを川に実際に移動することがなく長期間のこの波に乗るサーファーを許可する河床に形成できます。通常、彼らは大量の水が流れて、急速なペースで、大きな岩のような障害物を時を形成します。水が流れる岩の上に、それの後ろにクラッシュ、水の波と干渉する川の流れの反対の方向で大きな波を作成します。したがって、定在波が形成され、川サーファーは秒の問題の可能性が高い波が終わらないので、バランス、ことができます限り、それを乗ることができます。
スキップ先...
このコレクションのビデオ:

Now Playing
定在波
Physics II
49.8K 閲覧数

電界
Physics II
77.5K 閲覧数

電位
Physics II
105.0K 閲覧数

磁場
Physics II
33.6K 閲覧数

磁場下における電荷
Physics II
33.7K 閲覧数

オームの法則
Physics II
26.2K 閲覧数

シリーズと並列抵抗
Physics II
33.2K 閲覧数

静電容量
Physics II
43.8K 閲覧数

インダクタンス
Physics II
21.6K 閲覧数

RC/RL/LC 回路
Physics II
142.9K 閲覧数

半導体
Physics II
29.9K 閲覧数

光電効果
Physics II
32.7K 閲覧数

反射と屈折
Physics II
36.2K 閲覧数

干渉と回折
Physics II
91.2K 閲覧数

音の波とドップラー シフト
Physics II
23.5K 閲覧数
Copyright © 2023 MyJoVE Corporation. All rights reserved