Standing Waves
Обзор
Source: Arianna Brown, Asantha Cooray, PhD, Department of Physics & Astronomy, School of Physical Sciences, University of California, Irvine, CA
Standing waves, or stationary waves, are waves that appear not to propagate and are produced by the interference of two waves traveling in opposite directions with the same frequency and amplitude. These waves appear to vibrate up and down with no linear movement and are most easily identified in vibrating finite media like a plucked guitar string, water in a lake, or air in a room. For example, if a string is fixed at both ends and two identical waves are sent traveling along the length, the first wave will hit the end barrier and reflect back in the opposite direction, and the two waves will superpose to produce a standing wave. This motion is periodic with frequencies defined by the length of the medium and is a visual example of simple harmonic motion. Simple harmonic motion is motion that oscillates or is periodic, where the restoring force is proportional to the displacement, meaning the farther something is pushed, the harder it pushes back.
The goal of this experiment is to understand the roles of wave superposition and reflection in creating standing waves, and exploit those concepts to calculate the first few resonant frequencies, or harmonics, of standing waves on a slinky. Each frequency that an object produces has its own standing wave patterns, where the wave with the lowest possible frequency is called the fundamental frequency. A harmonic is a wave that has a frequency proportionate to the fundamental frequency by whole integer numbers.
Принципы
When two waves arrive at the same point in a path at the same time, they interfere. The amplitude of the resulting wave is the sum of the amplitude of the two linear waves (a direct result of the principle of superposition for linear waves). These two waves pass through one another without altering each other's paths or speeds. Constructive interference occurs when the amplitudes of the waves add, as they arrive in phase. When waves meet out of phase, their amplitudes subtract and they undergo destructive interference. If two waves with the same amplitude undergo destructive interference, their amplitudes cancel (Figure 1).
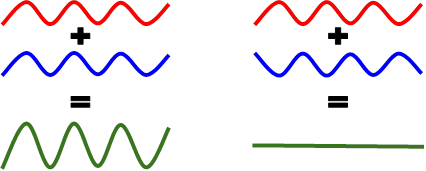
Figure 1: Two waves with equal amplitudes. Left: Constructive interference. Right: Destructive interference.
When a traveling wave meets a boundary (i.e., a different medium), some of its energy is reflected, some is transmitted into the new medium, and some is absorbed. For a perfect reflected wave scenario, where all of the energy is reflected and so no outside energy needs to be fed into the system, the energy is conserved. For a wave traveling on a medium with fixed boundaries, like a finite string, it will reflect off the end boundary and experience a 180 ° phase shift. If this process continues for an extended period of time, the waves bouncing back and forth between boundaries will interfere and create a stationary pattern known as a standing wave (Figure 2). The points of minimum amplitude (nodes) are points where the waves have opposite phases and cancel one another out. The points of maximum amplitude (antinodes) are points where the waves have the same phase and their respective amplitudes combine.

Figure 2: A standing wave on a medium of length 2λ. This is also a visual representation of the fourth harmonic.
The simplest standing wave, sometimes called the fundamental frequency, occurs when the length of the string L is ½λ, where λ is the wavelength. This means,

so the first vibration on a string with fixed points looks similar to the profile of a jump rope in motion. To make the next possible standing wave, a node is added in the center, and L becomes equivalent to λ: the result is a standing wave pattern with a shorter wavelength. Standing wave patterns with shorter wavelengths than the fundamental frequency are known as harmonics. Continuing to add nodes, we find that:
 (Equation 1)
(Equation 1)
where n is the number of nodes and the resulting harmonic is sometimes referred to as the nth harmonic. (Note: Some refer to the fundamental frequency as the first harmonic, while others refer to the n = 2 harmonic as the first harmonic).
In a propagating wave, energy is transferred along with the wave. As one section moves upward, it exerts a force on the next section, moving it through a displacement. In other words, work is done. Points that experience no displacement, like a node in a standing wave, cannot do work on the neighboring section. Thus, no energy is transmitted across a node on a string, and energy does not propagate in a standing wave. Instead, the energy of a standing wave alternates between elastic potential energy when the waves are momentarily stationary at their maximum amplitudes, and kinetic energy when the string is flat in the middle of an oscillation and a particle on an antinode has maximum directional speed. Additionally, consider a particle that is situated on a piece of string undergoing standing wave motion. Since standing waves result in simple back and forth motion, this particle appears to move back and forth at a measureable periodic rate. In standing waves, this oscillatory motion and the relationship between elastic and potential energy is described as simple harmonic motion, and thus has the observable properties of frequency f and period T. In the standing wave scenario, frequency is defined as the number of oscillation cycles per unit time, and period is the time required to make one complete cycle, or:
 (Equation 2)
(Equation 2)
In this lab, we will explore all of these properties by creating various waves and standing waves using a slinky.
Процедура
1. Observing the Superposition and Reflection of Slinky Pulses
- Stretch a slinky or steel spring lengthwise across a floor or hallway, with one student holding one end and another student holding the other. Use tape to mark two lengthwise 'barriers' about a foot away from the middle of the slinky, on each side. Repeat with barriers that are two feet away from the middle on each side.
- Take turns launching pulses (jerking the slinky a small distance horizontally and immediately snapping back to the starting point) with amplitudes that stay within the marked barriers.
- Next, try launching identical pulses with the same polarity simultaneously from both ends and notice what happens when the pulses meet. The superimposed wave should double in amplitude, cross the first taped barriers, and hit the second taped barriers.
- Now, launch identical pulses but with opposite polarity simultaneously and observe the pulse superpositions. The pulses should cancel one another out as they superimpose, and then continue traveling, never touching the barriers.
- Fix one end of the slinky by holding it tightly in position. Send a single pulse down to the fixed position and observe the wave's amplitude upon reflection. It will reflect back with opposite polarity.
2. Measuring the Frequency of Standing Waves on a Spring
- Stretch the slinky across a room or hallway and measure and record the stretched length.
- With one end fixed from motion (held tightly), gently begin sliding the other end horizontally in consistent motion until finding the fundamental frequency standing wave. For this harmonic, there should be only one wave crest with one amplitude moving back and forth, like the profile of a jump rope in motion. Use a stopwatch to record the time it takes for several wave cycles. One complete cycle starts when an antinode forms on one side, slides through the center to form an antinode on the other side, and then returns to its original position. Use these measurements to calculate the frequency, period, and wavelength for this wave using Equations 1 and 2.
- Increase the speed of the sliding end until the next harmonic (n = 2) is achieved. For this harmonic, there should be two wave crests on opposite sides moving in opposite directions, and it may look like the 2D projection of the letter 's' rotating. Measure the frequency, then calculate the period and wavelength for this wave. What is the ratio of this frequency to the fundamental frequency?
- Repeat the previous step for the next harmonic (n = 3).
Результаты
| Harmonic (n) | # Cycles | Total Time (s) | Frequency (Hz) | f/f0 | Period (s) | Wavelength (m) |
| 1 | 10 | 19.2 | 0.521 (f0) | 1 | 1.210 | 16 m |
| 2 | 10 | 9.75 | 1.026 | 1.97 | 0.975 | 8 m |
| 3 | 10 | 6.21 | 1.601 | 3.07 | 0.625 | 5.33 m |
Table 1: Section 2 - Stretched Spring Length = 8 m
In Section 1, principles of wave superposition and reflection in a finite medium are demonstrated and confirmed as pulses were sent down the length of the slinky. Specifically, we see that when two waves with identical amplitudes and phase meet, they undergo constructive interference and their amplitudes add. Similarly, we see that when two waves with opposite polarity (180 ° phase shift) and identical amplitudes meet, they undergo destructive interference and their amplitudes cancel. The latter of these principles is key in understanding standing wave patterns.
In Section 2, the nodes and antinodes of the slinky were easily visible at various frequencies. As the number of nodes increased, so did the frequency. The wavelength is inversely proportional to frequency, so there is naturally a decrease in wavelength. The frequencies of the harmonics are positive integer multiples of the fundamental frequency that correspond to n. For example, using the n = 2 harmonic, the frequency is measured and defined as the number of cycles per unit time:
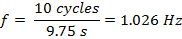
The period is defined as the inverse of the frequency (Equation 2) and is equal to:
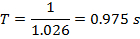
The wavelength is defined in Equation 1 as:

Finally, we can see the integer-proportional relationship between the harmonics and the fundamental frequency by calculating:
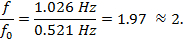
Заявка и Краткое содержание
In this experiment, the concepts of wave superposition and standing waves were explored in two demonstrations. Wave reflection and constructive versus destructive interference were visualized in the first demonstration. In the second, the changes in frequency and period were measured and higher harmonic frequencies were found to be integer multiples of the fundamental frequency.
A famous example of standing waves in the real world are the strings on a guitar, or any string instrument. In these instruments, a plucked string emits a particular frequency depending on how taut and dense the string is and the string length. Each string only makes certain notes because only certain standing waves, or harmonics, can form on that string. The musician can use their fingers to shorten the string length, creating a new node and new set of harmonics that are proportional to the fundamental frequency. Vibrations that are not at the right frequency, say fingers pinning the strings down onto a fret that doesn't allow for a standing wave at that string length, will sound odd and eventually cancel themselves out.
Standing waves also occur in nature, often in bounded bodies of water like lakes and harbors. Sometimes, they can form on a river bed allowing river surfers to ride this wave for an extended period of time without actually moving. Typically, they form when a large amount of water is flowing over an obstruction, like a big rock, at a rapid pace. As the water flows over the rock and crashes behind it, it creates a large wave in the opposite direction of the river's current that interferes with the incident wave of water. Thus, a standing wave is formed and river surfers can ride it for as long as their balance will allow them since the wave likely will not end in a matter of seconds.
Перейти к...
Видео из этой коллекции:

Now Playing
Standing Waves
Physics II
49.8K Просмотры

Electric Fields
Physics II
77.5K Просмотры

Electric Potential
Physics II
105.0K Просмотры

Magnetic Fields
Physics II
33.6K Просмотры

Electric Charge in a Magnetic Field
Physics II
33.7K Просмотры

Investigation Ohm's Law for Ohmic and Nonohmic Conductors
Physics II
26.2K Просмотры

Series and Parallel Resistors
Physics II
33.2K Просмотры

Capacitance
Physics II
43.8K Просмотры

Inductance
Physics II
21.6K Просмотры

RC/RL/LC Circuits
Physics II
142.9K Просмотры

Semiconductors
Physics II
29.8K Просмотры

Photoelectric Effect
Physics II
32.7K Просмотры

Reflection and Refraction
Physics II
36.2K Просмотры

Interference and Diffraction
Physics II
91.2K Просмотры

Sound Waves and Doppler Shift
Physics II
23.5K Просмотры
Авторские права © 2025 MyJoVE Corporation. Все права защищены