Stehende Wellen
Überblick
Quelle: Arianna Brown, Asantha Cooray, PhD, Department of Physics & Astronomie, School of Physical Sciences, University of California, Irvine, CA
Stehende Wellen oder stehende Wellen sind Wellen, die nicht scheinen, zu propagieren und entstehen durch die Interferenz von zwei Wellen mit gleicher Frequenz und Amplitude in entgegengesetzter Richtung unterwegs. Diese Wellen erscheinen oben und unten ohne lineare Bewegung zu vibrieren und am leichtesten in vibrierenden finite Medien wie einer gezupften Gitarrensaiten, Wasser in einem See oder Luft in einem Raum identifiziert. Zum Beispiel wenn eine Zeichenfolge an beiden Enden fixiert wird und zwei identische Wellen Reisen entlang der Länge gesendet werden, die erste Welle wird drücken Sie die Ende-Barriere und zurück in die entgegengesetzte Richtung, und die zwei Wellen überlagern werden, um eine stehende Welle erzeugen. Diese Bewegung ist periodisch mit Frequenzen, die durch die Länge des Mediums definiert und ist ein visuelles Beispiel für einfache harmonische Bewegung. Einfache harmonische Bewegung ist Bewegung, die schwankt oder ist periodisch, wo die Rückstellkraft ist proportional zur Vertreibung, d. h. je weiter etwas wird geschoben, je härter es drängt zurück.
Das Ziel dieses Experiments ist es, die Rollen der Welle Überlagerung und Reflexion bei der Schaffung von stehenden Wellen zu verstehen, und nutzen diese Konzepte um die ersten paar Resonanzfrequenzen zu berechnen, oder Obertöne, stehende Wellen auf ein aufreizendes. Jede Frequenz, die ein Objekt produziert hat eine eigene stehende Wellenmuster, wo die Welle mit der niedrigsten möglichen Frequenz der Grundfrequenz genannt wird. Eine harmonische ist eine Welle, die eine Frequenz proportional zur Grundfrequenz von Ganzzahl zahlen hat.
Grundsätze
Wenn zwei Wellen an der gleichen Stelle in einem Pfad zur gleichen Zeit ankommen, stören sie. Die Amplitude der resultierenden Welle ist die Summe der Amplitude der zwei lineare Wellen (eine direkte Folge des Grundsatzes der Überlagerung für lineare Wellen). Diese zwei Wellen durchlaufen einander ohne Änderung des anderen Pfade oder Geschwindigkeiten. Konstruktive Interferenz tritt auf, wenn die Amplitude der Wellen hinzufügen, wie sie in Phase zu gelangen. Wenn Wellen aus der Phase treffen, deren Amplituden subtrahieren und destruktive Interferenzzu unterziehen. Wenn zwei Wellen mit der gleichen Amplitude destruktive Interferenz unterziehen, stornieren ihre Amplituden (Abbildung 1).
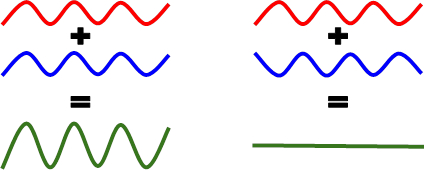
Abbildung 1: Zwei Wellen mit gleicher Amplitude. Links: Konstruktive Interferenz. Rechts: Destruktive Interferenz.
Wenn eine Reisende Welle eine Begrenzung (d.h. ein anderes Medium) stößt, etwas von seiner Energie spiegelt sich, einige in das neue Medium übertragen wird, und wird absorbiert. Für eine perfekte reflektierte Welle Szenario, wo all die Energie spiegelt sich und also keine externe Energie in das System eingespeist werden muss, ist die Energie erhalten. Für eine Welle auf ein Medium mit festen Grenzen, wie eine endliche Zeichenfolge wird von Ende Begrenzung reflektiert und erleben Sie eine 180° Phasenverschiebung. Wenn dieser Vorgang wiederholt sich für einen längeren Zeitraum hinweg, die Wellen hin und her springen zwischen den Grenzen stören und erstellen Sie eine stationäre Muster bekannt als eine stehende Welle (Abbildung 2). Die minimale Amplitude (Knoten) sind Punkte, wo die Wellen haben entgegengesetzte Phasen und heben sich gegenseitig auf. Die maximale Amplitude (Schwingungsknoten) sind Punkte, wo die Wellen sind gleichphasig und ihre jeweiligen Amplituden zu kombinieren.

Abbildung 2: Eine stehende Welle auf ein Medium der Länge 2λ. Dies ist auch eine visuelle Darstellung des vierten harmonischen.
Die einfachste stehende Welle, manchmal genannt die Grundfrequenz tritt auf, wenn die Länge der Zeichenfolge L ½λ, wo λ ist die Wellenlänge. Dies bedeutet,

So sieht die erste Schwingung auf eine Zeichenfolge mit festen Punkten ähnlich wie das Profil der ein Springseil in Bewegung. Um die nächste mögliche stehende Welle zu machen, ist ein Knoten in der Mitte hinzugefügt, und L wird λ entspricht: das Ergebnis ist eine stehende Wellenmuster mit einer kürzeren Wellenlänge. Stehende Wellenmuster mit kürzeren Wellenlängen als die Grundfrequenz werden Obertöne genannt. Weiterbildung zu Knoten hinzufügen, finden wir, dass:
 (Gleichung 1)
(Gleichung 1)
wo n ist die Anzahl der Knoten und die daraus resultierende harmonische wird manchmal alsder Oberwelle n bezeichnet. (Hinweis: einige beziehen sich auf die Grundfrequenz als die Grundschwingung, während andere beziehen sich auf n = 2 harmonische als die Grundschwingung).
In einer verbreitende Welle wird zusammen mit der Welle Energie übertragen. Während ein Teil nach oben bewegt, übt es eine Kraft auf den nächsten Abschnitt durch eine Verschiebung zu bewegen. Das heißt, ist die Arbeit getan. Punkte, die keine Verschiebung, wie ein Knoten in einer stehenden Welle erleben können nicht auf den benachbarten Abschnitt arbeiten. So werden über einen Knoten an einer Schnur keine Energie übertragen, und Energie wird nicht in eine stehende Welle ausbreiten. Stattdessen wechselt die Energie einer stehenden Welle zwischen elastischen potentielle Energie, wenn die Wellen kurzzeitig stationär an ihrer maximalen Amplituden sind und kinetische Energie, wenn die Zeichenfolge in der Mitte eine Schwingung und ein Teilchen auf ein Bauch flach ist direktionale Höchstgeschwindigkeit. Darüber hinaus berücksichtigen Sie einen Partikel, der auf ein Stück Schnur in der stehenden Wellenbewegung befindet. Da stehende Wellen in einfachen hin und her Bewegung führen, scheint dieses Teilchen auf eine messbare periodische Verzinsung hin-und herbewegen. In stehender Wellen diese oszillierende Bewegung und die Beziehung zwischen elastischen und potentielle Energie bezeichnet man als einfache harmonische Bewegung und hat somit die beobachtbaren Eigenschaften der Frequenz f und Periodendauer T. Im Szenario stehende Welle Frequenz ist definiert als die Anzahl der Schwingungen pro Zeiteinheit Zyklen, und der Zeitaufwand beträgt zu einem Zyklus, oder:
 (Gleichung 2)
(Gleichung 2)
In diesem Labor untersuchen wir alle diese Eigenschaften durch verschiedene Wellen und stehende Wellen mit ein slinky.
Verfahren
(1) unter Beachtung der Überlagerung und Reflexion der Slinky Impulse
- Erstrecken Sie sich eine slinky oder Stahl Feder längs einer Etage oder im Gang, ein Student mit einem Ende mit einem anderen Studenten halten die andere. Verwenden Sie Band, um zwei Länge "Barrieren" über einen Fuß weg von der Mitte der slinky, auf jeder Seite zu markieren. Mit Barrieren, die zwei Füße weg von der Mitte auf jeder Seite wiederholen.
- Abwechselnd starten Impulse (Rucken slinky kleinem Abstand horizontal und sofort schnappte zurück zum Ausgangspunkt) mit Amplituden, die innerhalb der markierten Hindernisse bleiben.
- Als nächstes versuchen Sie identische Impulse mit der gleichen Polarität gleichzeitig von beiden Seiten zu starten und bemerken Sie, was passiert, wenn die Impulse zu erfüllen. Die übereinander liegenden Welle sollte doppelte Amplitude, überqueren Sie die erste mit Klebeband Barrieren und traf die zweite mit Klebeband Barrieren.
- Nun starten identisch Impulse, aber mit entgegengesetzter Polarität gleichzeitig und die Puls-Überlagerungen zu beobachten. Die Hülsenfrüchte sollten einander aufheben, da sie überlagern, und dann reisen weiter, nie berühren die Barrieren.
- Befestigen Sie ein Ende der slinky von hielt sie fest in Position. Senden Sie einen einzigen Puls nach unten in die feste Position und beobachten Sie die Wellenamplitude nach reiflicher Überlegung. Es wird wieder mit entgegengesetzter Polarität widerspiegeln.
2. messen die Frequenz der stehenden Wellen auf einer Feder
- Erstrecken Sie die slinky sich über einen Raum oder Flur und Messen und aufzuzeichnen die gestreckte Länge.
- Beginnen Sie mit einem Ende fest von Motion (fest gehalten), sanft Ende horizontal in konsequente Bewegung bis das finden der Grundfrequenz stehende Welle schieben. Für diese harmonische sollte nur ein Wellenberg mit einer Amplitude hin-und herbewegen, wie das Profil der ein Springseil in Bewegung. Verwenden Sie eine Stoppuhr zum Speichern, die mehrere Welle Zyklen benötigt. Ein Gesamtzyklus beginnt bei einer Bauch-Formen auf der einen Seite gleitet durch das Zentrum, ein Bauch auf der anderen Seite bilden und dann in seine Ausgangsposition zurück. Verwenden Sie diese Messungen, um die Häufigkeit, Dauer und Wellenlänge für diese Welle mit Gleichungen 1 und 2zu berechnen.
- Erhöhen Sie die Geschwindigkeit der verschiebbaren Ende bis die nächste harmonische (n = 2) erreicht ist. Für diese harmonische sollte zwei Wellenbergen auf gegenüberliegenden Seiten in entgegengesetzte Richtungen bewegen, und es kann aussehen wie die 2D Projektion von des Buchstabens "drehen. Messen Sie die Frequenz zu, dann berechnen Sie die Zeit und die Wellenlänge für diese Welle. Wie ist das Verhältnis dieser Frequenz, die Grundfrequenz?
- Wiederholen Sie die vorherigen Schritt für die nächste harmonische (n = 3).
Ergebnisse
| Harmonische (n) | # Zyklen | Gesamtzeit (s) | Frequenz (Hz) | f/f0 | Periode (s) | Wellenlänge (m) |
| 1 | 10 | 19.2 | 0.521 (f-0) | 1 | 1.210 | 16 m |
| 2 | 10 | 9,75 | 1.026 | 1.97 | 0,975 | 8 m |
| 3 | 10 | 6.21 | 1.601 | 3.07 | 0,625 | 5,33 m |
Tabelle 1: Abschnitt 2 - gestreckt Federlänge = 8 m
In Abschnitt 1 sind Grundsätze der Welle Überlagerung und Reflexion in einem endlichen Medium nachgewiesen und bestätigt, wie Impulse entlang der slinky gesendet wurden. Insbesondere sehen wir, dass wenn zwei Wellen mit identischen Amplitude und Phase treffen, sie, konstruktiven Interferenz durchmachen und fügen Sie ihre Amplituden. In ähnlicher Weise sehen wir, dass wenn zwei Wellen mit entgegengesetzter Polarität (180° Phasenverschiebung) und identische Amplituden treffen, destruktive Interferenz zu unterziehen und ihre Amplituden zu stornieren. Letzteres dieser Prinzipien ist Schlüssel für das Verständnis der stehenden Wellenmuster.
In Abschnitt 2 wurden die Knoten und Bäuche von der slinky leicht sichtbar bei verschiedenen Frequenzen. Mit zunehmender Anzahl von Knoten haben also die Frequenz. Die Wellenlänge ist umgekehrt proportional zur Frequenz, so gibt es natürlich eine Abnahme der Wellenlänge. Die Frequenzen der harmonischen sind positive ganzzahlige Vielfache der Grundfrequenz, die nentsprechen. Verwenden Sie beispielsweise n = 2 harmonisch, die Frequenz gemessen und definiert als die Anzahl der Zyklen pro Zeiteinheit:
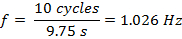
Die Periode ist definiert als der Kehrwert der Frequenz (Gleichung 2) und ist gleich:
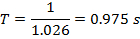
Die Wellenlänge wird in Gleichung 1 als definiert:

Schließlich sehen wir die Ganzzahl-proportionale Beziehung zwischen der Obertöne und die Grundfrequenz durch die Berechnung:
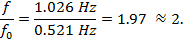
Anwendung und Zusammenfassung
In diesem Experiment wurden die Konzepte der Welle Überlagerung und stehende Wellen in zwei Demonstrationen erkundet. Welle Reflexion und konstruktive und destruktive Interferenz wurden in die erste Demonstration visualisiert. Im zweiten Fall wurden die Veränderungen in Häufigkeit und Zeitraum gemessen und höhere harmonischen Frequenzen erwiesen sich ganzzahlige Vielfache der Grundfrequenz.
Ein berühmtes Beispiel für stehende Wellen in der realen Welt sind die Saiten auf eine Gitarre oder ein String Instrument. Bei diesen Instrumenten einer gezupften Saite strahlt eine bestimmte Frequenz je nachdem, wie straff und dicht die Zeichenfolge ist und die Länge der Zeichenfolge. Jede Saite macht nur bestimmte Noten, weil nur bestimmte stehende Wellen oder Oberwellen, auf diese Zeichenfolge bilden können. Die Musiker können ihre Finger, um die Länge der Zeichenfolge zu verkürzen, erstellen einen neuen Knoten und neues set von Oberschwingungen, die proportional zur Grundfrequenz sind. Schwingungen, die nicht in der richtigen Frequenz sagen Finger fixieren die Saiten nach unten auf einen Bund, die nicht für eine stehende Welle auf die Länge der Zeichenfolge zu ermöglichen, wird merkwürdig klingen und schließlich heben sich auf.
Stehende Wellen auftreten, auch in der Natur oft in begrenzten Gewässern wie Seen und Häfen. Manchmal können sie auf einem Flussbett Fluss-Surfer auf dieser Welle für einen längeren Zeitraum hinweg zu reiten, ohne tatsächlich zu bewegen erlaubt bilden. In der Regel bilden sie, wenn eine große Menge Wasser über ein Hindernis, wie ein großer Stein, in einem rasanten Tempo fließt. Wie das Wasser über den Felsen fließt und dahinter abstürzt, schafft es eine große Welle in die entgegengesetzte Richtung des Flusses Strömung, die mit der einfallenden Welle des Wassers stört. So bildet sich eine stehende Welle und Fluss-Surfer können es für Reiten, solange ihr Gleichgewicht wird ihnen erlauben, da die Welle wahrscheinlich nicht in einer Angelegenheit von Sekunden enden wird.
pringen zu...
Videos aus dieser Sammlung:

Now Playing
Stehende Wellen
Physics II
49.8K Ansichten

Elektrische Felder
Physics II
77.5K Ansichten

Elektrisches Potential
Physics II
105.0K Ansichten

Magnetische Felder
Physics II
33.6K Ansichten

Elektrische Ladung in einem Magnetfeld
Physics II
33.7K Ansichten

Ohmsches Gesetz
Physics II
26.2K Ansichten

Reihen- und Parallelwiderstände
Physics II
33.2K Ansichten

Kapazität
Physics II
43.8K Ansichten

Induktivität
Physics II
21.6K Ansichten

RC/RL/LC-Schaltungen
Physics II
142.9K Ansichten

Halbleiter
Physics II
29.8K Ansichten

Photoeffekt
Physics II
32.7K Ansichten

Reflexion und Brechung
Physics II
36.2K Ansichten

Interferenz und Beugung
Physics II
91.2K Ansichten

Schallwellen und Dopplereffekt
Physics II
23.5K Ansichten
Copyright © 2025 MyJoVE Corporation. Alle Rechte vorbehalten