RC/RL/LC 回路

ソース: 龍 p. 陳博士は、物理学科 & 天文学、科学の大学、パーデュー大学、ウェスト ラファイエット, インディアナ

抵抗器 (R)、インダクタ (L)、コンデンサー (C) は、それぞれ個別の動作に重要な回路要素。抵抗はエネルギーを散らすし、その電流に比例する電圧とオームの法則に従います。コンデンサーは、インダクタの電圧、電流の変化の割合に比例して磁気エネルギーを格納、その電圧の変化の割合に比例する電流との電気エネルギーを格納します。これらの回路素子を組み合わせれば、電流または電圧が面白い方法で、時間とともに変化する可能性が。このような組み合わせは、交流電流 (AC) 回路、ラジオ、および電気フィルターの時間または周波数依存電気信号を処理する使用されます。この実験は抵抗器-コンデンサー (RC) の時間依存挙動を示す抵抗器インダクタ (RL)、およびインダクタ コンデンサー (LC) 回路。実験のデモンストレーション時にコンデンサーやインダクタを直列に接続した電球 (抵抗) を用いた RC と RL 回路の過渡 (とスイッチオン) に接続する電源装置。実験は、LC 回路の振動現象も示します。

図 1に示されている、(電圧出力 V)、電圧源に接続されているコンデンサー (キャパシタンス C) と一緒のシリーズ (抵抗 R) と抵抗を検討してください。電圧源が時間tにつけ = 0、抵抗 r. によって、回路の流れを開始する時間依存現在私(t)この電流は、それ「流れるように」コンデンサーとも呼ばれる「充電電流」、コンデンサーの (すなわち、コンデンサーの反対側板反対電荷をもたらす) コンデンサーで時間依存の電圧ドロップ V_cを開発します。総電圧 V の電源電圧から抵抗での電圧降下間で共有されるので (ある私 ×R) とコンデンサー (V_C) の間で。

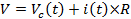(関係式 1)

初めに (t = 0 の出力 V の電源電圧になって後にすぐに)、コンデンサーには任意の電圧、およびしたがって V_Cを身につける機会がなかった (t = 0) = 0 と (式 1) によると私(t = 0) = V/r.時間が進むにつれて、料金は、コンデンサーの上に構築し V_cが増加し、したがって私(t) を減少させるでしょう。さらに、これらの料金は追加料金コンデンサーに到着を撃退する傾向がある (すなわち、反対の充電プロセス)。十分な時間の経過すると、この充電処理は停止し、したがってi(t→∞) = 0 および V_c(t→) = V。つまり、これ以上電流が流れるとコンデンサーの動作このオープン スイッチ、充電、定常状態と、コンデンサーが完全に充電して今 (またはそれを渡ってドロップ電圧ソースから全電圧 V があります)。一般に、コンデンサーはより高い周波数の過渡電流、以下を実施しています、またはすべてではない低周波や定常状態 (DC) 現在実施しています。

完全な定量的な時間依存現在私(t) ことで解決できます。

(式 2)

どこ

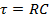(式 3)

"RC"回路「RC 時定数」として知られており、一般に RC 回路の応答のタイム スケールの特徴 (ここでは、電流の変化) 入力の過渡変化時 (ここでは電圧供給切り替え)。このような時間依存電流式 2によって与えられたとは、図 1に描かれています。

この場合、RC の時はまたコンデンサーを充電するため特徴的な時間スケールを表します。すなわち、(電圧) と完全に充電されたコンデンサーを (短い線で図 1の電圧ユニットの取り付けに対応する) 閉鎖回路を形成する抵抗を直結して、抵抗に流れる電流再度続く方程式 2コンデンサーを充放電の時間スケールです。

インダクタ、または図 2に示すように 1 つなどの"RL"回路の直列に抵抗の類似の分析が可能です。ただし、インダクタの動作とは逆キャパシタ、インダクタを (定常状態の電流インダクタが短い少し抵抗線として機能)、低周波より行っていますという意味で行っていますが、あまり高い周波数でまたは一時的な状況で (これはインダクタは、常に、現在の変更に反対しようと)。その結果、現在は私(t) 時間tでスイッチを閉じると、図 2に示す RL 回路の流れ = 0 (または V の出力電圧で切り替え) になります。

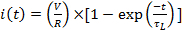(関係式 4)

どこ

(式 5)

応答の一般的な特徴的な時間スケールである (ここでは電流の変化) 入力の過渡変化時に RL 回路の (ここでは電圧供給切り替え)。メモここでは、私(t = 0) = 0、インダクタが現状で突然変更に反対するしようし、当初、(これは同じ抵抗を流れる電流) インダクタに流れる電流にはゼロの値 (前に電源をオンにすると)、その最初から変更するチャンスがなかった。回路の定常状態に達すると後は、現在はもはや時間と変化し、インダクタ動作短いワイヤと確かに私(t→∞) = V/R式 4によると。(現在は、0 から増加し、V/R を指数関数的に近づく) この動作は図 2、およびそれが反対に注意で描かれている (図 1電流が V/R から減少し、0 に指数関数的に減衰方程式 2 ・ RC 回路の動作から。

RC や RL 回路における指数時間依存性抵抗の散逸の性質に関連しています。対照的に、コンデンサーは図 3 aで示されているものなどのごくわずかな抵抗とインダクタに直結"LC"回路が動作、振動または「共鳴」。図 3 aは、コンデンサー、インダクタを接続して V のドロップ電圧を持っている初期充電を示しています (それまでは電流と最初) 時間t = 0。1 つは、コンデンサー (インダクタに同じ) に後続の電圧が次の振動 (正弦波) の時間依存性を持っていることを示すことができます。

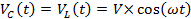(関係式 6)

どこ

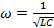(関係式 7)

「周波数」または「共振周波数」(ここでは、周波数"とは、角周波数を指します) LC 回路の。インダクタに流れる電流です。

(関係式 8)

コンデンサーは最初、インダクタ (V_C(t) 減少とi(t) の増加) を通して放電されます。Ωtが π/2 になったら、コンデンサーが完全に放電 (V_C = 0) と、インダクタの最大電流が流れる。(Ωtが π に達したら、V_C(t) 達する V) 逆極性に再び (インダクタに流れる電流) によってコンデンサーへ充電し、その後、再度放電と (ωt 3 π/2 に達すると完全に放電)、充電器 ωtに達すると 2 π = V を V_Cの元の極性に。サイクル時間 (t) の期間に繰り返されます

図 3 bで描かれているようなの振動現象は、コンデンサーとインダクタ (コンデンサーは電流による磁場下におけるインダクタの店エネルギーと電圧降下による電界のエネルギーを格納する) 相互間の電磁エネルギーの交換にも対応します。回路の抵抗はありません (およびしたがってないの損失) の理想的な状況で振動は無期限行くことができます。いくつかの存在下での例図 3 c「RLC」回路として知られている (外部電源供給がない) 場合、そのような振動減衰は、下図の回路での抵抗 (散逸)、描かれ図 3 dで、十分な時間の経過後両方の電圧電流ゼロに達するでしょう。

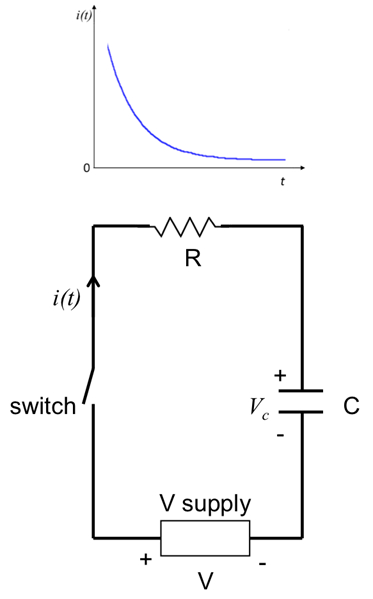
図 1:図の RC 回路、コンデンサー (C) と直列に抵抗 (R) スイッチと電源電圧に接続されています。(式 2によって与えられる) 代表的な時間依存の電流は、図の上に描かれています。

図 2:インダクタ (L) と直列に抵抗 (R) の RL 回路を示す図はスイッチで電源に接続されています。(方程式 4によって与えられる) 代表的な時間依存電流は、上図に描かれています。

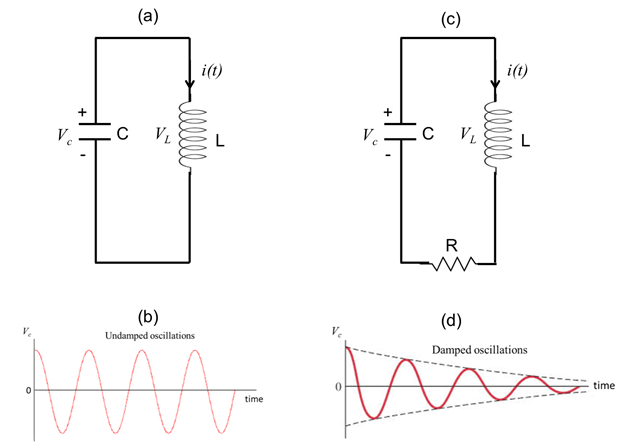
図 3:(、) インダクタ (L) との LC 回路図と接続される回路内のコンデンサー (C)。(b) 代表的な時間依存電圧コンデンサー、(与えられたもの数式 6) 不減衰振動を示します。(c) も RLC 回路として知られている一連の抵抗 (R)、LC 回路を示す図。(d) は代表的な時間依存電圧減衰振動を表示 (c) に示す回路のコンデンサー。

1. オシロ スコープを使用してください。

1. オシロ スコープ、(いくつかの Ω の抵抗 R) と小さな電球、スイッチと DC 電圧供給 (または 1.5 V バッテリーまたは) を取得します。
2. オープン スイッチを図 4に示すように、回路を接続します。この実験では接続ケーブル、クランプ、作ることができるまたは受信機器のポートにバナナプラグします。
3. 選択対 1 1 に近い範囲にオシロ スコープの時間スケールに近い範囲にオシロ スコープの垂直軸を選択する s。
4. (このように電球の切り替え) スイッチを閉じます。オシロ スコープ画面上のトレース (「波形」) と電球を観察します。オシロ スコープ、電球に並列に接続されている電球の電圧の測定が、この電圧は電球を流れる電流に比例します。
5. (このように電球をオフ)、スイッチをもう一度開きます。再びオシロ スコープ画面上のトレース (「波形」) と同様に、電球を観察します。
6. 必要な場合は、1.4 と 1.5 では、手順を繰り返します。

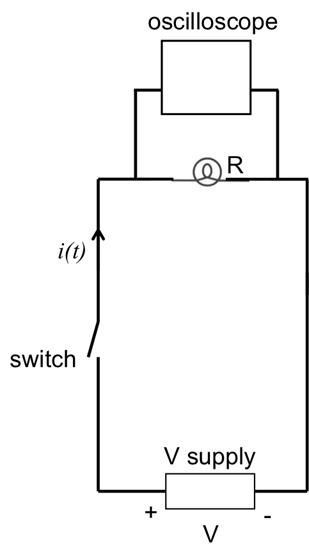
図 4:スイッチで電源に接続されている電球を示す図。オシロ スコープは、その電圧 (電流に比例した) を測定する電球に並列に接続されます。

2. RL 回路

1. 1 milliHenry (mH) のインダクタンス L とインダクタを取得します。
2. (オシロ スコープで電球に並列に接続)、シリーズのインダクタを電球に接続し、オープン スイッチで供給電圧を図 5 aに示すように。
3. スイッチを閉じます。電球としてオシロ スコープで波形を観察します。
4. スイッチを開きます。(最初の電球と同じような) の他の電球を入手して、図 5 bに示すように、最初の電球を並列に接続します。
5. 手順 2.3 (スイッチを閉じる)、繰り返し、電球とオシロ スコープを観察します。

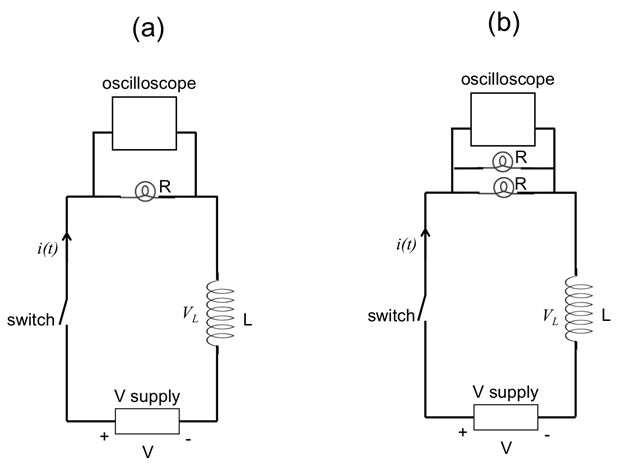
図 5:図 (a) または (b) 抵抗 (R) として 2 つの並列電球 1 つの電球での RL 回路を示しています。オシロ スコープは、light bulb(s) の light bulb(s)、現在の合計に比例した電圧を測定すると並列に接続されます。

3. RC 回路

1. 1 ファラド (F) の容量のコンデンサーを入手します。
2. (オシロ スコープに並列につながった) 電球シリーズのコンデンサーを接続し、一緒に電圧を供給オープン スイッチを図 6 aに示すように。これはインダクタ、コンデンサー取替えを除いて 2.2 の手順で接続図 5 aに示すような回路に対応します。
3. スイッチを閉じます。電球としてオシロ スコープで波形を観察します。
4. スイッチを開きます。図 6bに示すように、最初の電球を並列に 2 番目の電球を接続します。
5. 手順 3.3 (スイッチを閉じる)、繰り返し、電球とオシロ スコープを観察します。

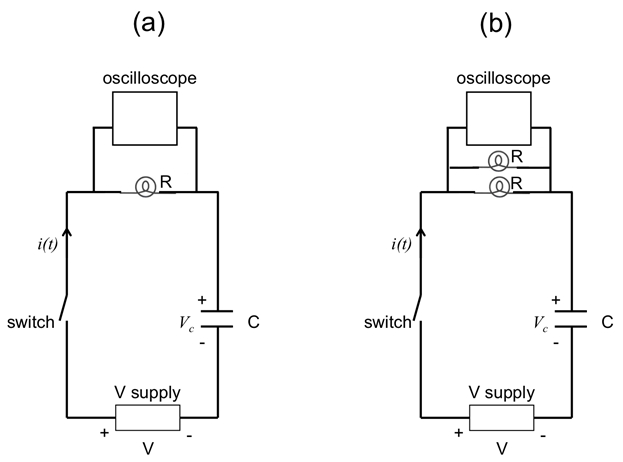
図 6:図 (a) または (b) 抵抗 (R) として 2 つの並列電球 1 つの電球での RC 回路を示しています。オシロ スコープは、light bulb(s) の light bulb(s)、現在の合計に比例した電圧を測定すると並列に接続されます。

3. LC 回路

1. 図 7に示すように、8 の mH のインダクタ別オープン スイッチ (スイッチ #2) シリーズと一緒に 10 μ F のコンデンサーを並列に接続します。充電コンデンサーを持っている #1 スイッチを閉じます。実験のこの部分では、電球は使用されません。
2. 図 7に示すように、コンデンサーと並列にオシロ スコープを接続します。
3. 今開いている #1、すぐにまたすぐスイッチ #2。オシロ スコープを観察します。

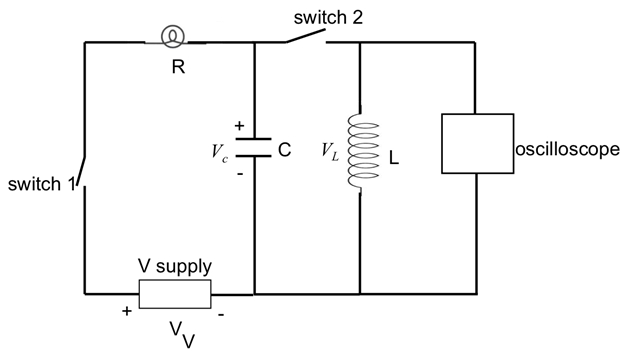
図 7:スイッチ インダクタ (L) を示す図は、図 6で勉強シリーズ RC 回路の一部であるコンデンサー (C) に並列に接続します。オシロ スコープは、その電圧を測定するインダクタに並列に接続されます。

ステップ 1、電球は「瞬時に」オンとオフにする (手順 1.4) 開閉の手順で 1.5 スイッチ。代表的なオシロ スコープ トレースは、図 8のとおりです。

2.3 ステップ スイッチを閉じた後それが観察できる電球をオンにするための小さいが顕著な時間かかる (の代わりに即座に手順 1 に従って)。2 つの並列の電球を使用する場合 (2.5 ステップ)、前の例 (手順 2.3) と比較してに電球の長い時間がかかります。これは、2 つの並列の電球を与えるより小さい抵抗 (R) とこのように長い時定数 τ_L = L/R RL 回路 (時定数ないこと丁度 2 回限り 2 つの電球にまったく同じの抵抗がなく、回路の他の非取るにたらない抵抗がありますので注意してください)。2 つの場合のオシロ スコープの代表的な痕跡は、図 9のとおりです。「オン」時オシロ スコープで測定スケールは 〜 ms 定数 τ_Lインダクタンスと電球抵抗値に基づく予定時刻と一致しているとします。

ステップ 3.3 スイッチを閉じた後それが観察できる絶滅する前に簡潔に電球が光ります。2 つの並列の電球を使用した場合 (ステップ 3.5)、前の例 (手順 3.3) と比較して死ぬため電球の短い時間がかかります。これは 2 つの平行光の電球を与えるより小さい抵抗 (R)、およびこうして短い RC 時定数 τ = RC。2 つの場合のオシロ スコープの代表的な痕跡は、図 10のとおりです。タイム スケールの「オン」~ 1 s キャパシタンスと電球の抵抗の値に基づいて定数 τ 予定時刻と一致しています。

ステップ 4.3、図 3 bで描かれているものなど振動電圧の3 dをオシロ スコープで観察できます。回路を接続するワイヤの有限抵抗のためいくつかの減衰振動を生じること。ミリ秒の順序、振動の周期が予想される LC 発振周期と一致 (2 π) キャパシタンスと抵抗の値に基づいて。

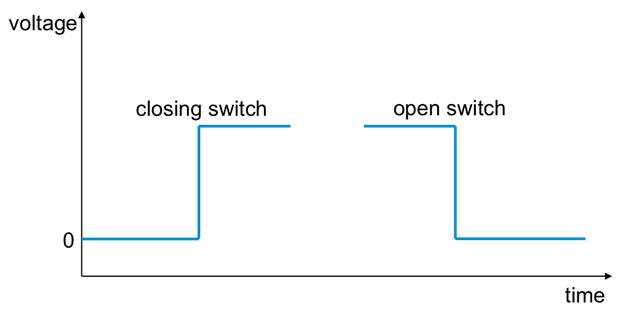
図 8:代表的なオシロ スコープ トレース (または波形」) は電源電圧に接続されている電球の電圧を直接測定ときスイッチを閉じるか開くと、図 4に描かれている実験で観察されることがあります。

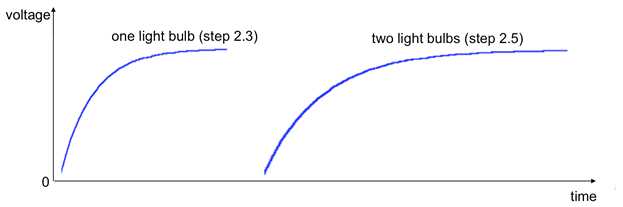
図 9:代表的なオシロ スコープ トレース (または波形」) に示す図 5インダクタと電圧源のシリーズで接続されている電球の間で電圧を測定する実験でスイッチを閉じるときを観察することがあります。

図 10:代表的なオシロ スコープ トレース (または波形」)図 6コンデンサーと電圧源のシリーズで接続されている電球の間で電圧を測定する実験でスイッチを閉じるときを観察することがあります

この実験では、RC や RL 回路の時定数の抵抗を変更するしくみの時間依存応答 (指数回転オン/オフ) を示しています。また、LC 回路の振動応答を示した。

RC、RL と LC 回路は回路の多くのアプリケーションで不可欠なビルディング ブロックです。たとえば、RC と RL 回路は通常フィルター (コンデンサーは、高周波信号を渡すが、反対はインダクタの本当に低周波信号をブロックする傾向があるという事実の利点を取って) として使用します。たとえば、デリバティブや電気信号の積分を取って電気信号処理に便利ですも。電気の「発振器」または共振回路の簡単な例の LC 回路でアンプ ラジオのチューニングなどに使用される回路の一般的なコンポーネント

実験の著者は、材料準備のためゲイリー ハドソンとビデオの手順を示すため Chuanhsun Li の支援を認めています。