Circuitos RC/RL/LC

Fuente: Yong P. Chen, PhD, Departamento de física & Astronomía, Facultad de Ciencias, Universidad de Purdue, West Lafayette, IN

Resistencias (R), condensadores (C) y bobinas (L) son un elemento importante del circuito con distintos comportamientos. Una resistencia disipa energía y obedece ley del ohmio, con la tensión proporcional a su corriente. Un condensador almacena energía eléctrica, con su corriente proporcional a la tasa de cambio de su tensión, mientras que un inductor almacena energía magnética, con su tensión proporcional a la tasa de cambio de su corriente. Cuando se combinan estos elementos de circuito, pueden causar la corriente o voltaje que varíe con el tiempo vario, interesantes formas. Tales combinaciones se utilizan para procesar señales eléctricas o frecuencia-dependiente del tiempo, como por ejemplo en circuitos de corriente alterna (CA), las radios y filtros eléctricos. Este experimento demostrará el comportamiento dependiente del tiempo del resistencia-condensador (RC), resistencia-inductor (RL) y circuitos de inductor-capacitor (LC). El experimento demostrará el comportamiento transitorio de circuitos RC y RL utilizando una bombilla (resistencia) conectada en serie a un condensador o un inductor, al conectarse (y encendido) una fuente de alimentación. El experimento también demostrará el comportamiento oscilatorio de un circuito LC.

Considerar una resistencia (con resistencia R) en serie de un condensador (con capacitancia C), junto conectada a una fuente de tensión (con salida de voltaje V), como se muestra en la figura 1. Si la fuente de tensión se conecta en el tiempo t = 0, un dependiente del tiempo corriente (t) empezará a fluir en el circuito, a través del resistor R. Esta corriente es también conocida como la "corriente de carga" para el condensador, ya que "desemboca" el condensador (es decir, trae cargas opuestas a las placas opuestas en el condensador) para desarrollar un voltaje dependientes del tiempo de caída de V_c a través del condensador. Puesto que la tensión total V de la fuente de voltaje se reparte entre la caída de tensión en la resistencia (que es i ×R) y que a través del condensador (V_C):

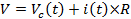(Ecuación 1)

Al inicio (t = 0, inmediatamente después de encender la fuente de tensión con salida de V), el condensador no ha tenido la oportunidad de desarrollar cualquier tensión y por lo tanto V_C(t = 0) = 0 y (según la ecuación 1), (t = 0) = V/R. Medida que avanza el tiempo, los cargos se acumulan en el condensador V_c aumentará y así (t) disminuye. Además, estas cargas tienden a rechazar cargos adicionales en el condensador (es decir, oponerse a la carga de proceso). Después de una cantidad suficiente de tiempo, carga de este proceso se detiene y por lo tanto i(t→∞) = 0 y V_c(t→) = V. Esto significa que el condensador está ahora cargado (o tiene el V el voltaje completo de la fuente de voltaje que cae a través de él), los flujos no más actuales y el condensador se comporta como un interruptor abierto en este completamente cargada, estado estacionario. En general, un condensador realiza más de mayor frecuencia o transitorios de corriente, mientras se lleva a cabo menos o nada de menor frecuencia o corriente de estado estacionario (DC).

El completo, cuantitativa dependiente del tiempo corriente (t) puede ser resuelto por:

(Ecuación 2)

donde,

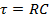(Ecuación 3)

se conoce como la "constante de tiempo RC" del circuito "RC" y caracteriza en general la escala de tiempo para la respuesta del circuito RC (aquí el cambio en la corriente) a un cambio transitorio en una entrada (aquí el encendido de la fuente de tensión). Tal una corriente dependiente del tiempo dado por la ecuación 2 se representa en la figura 1.

En este caso, el tiempo RC también representa la escala de tiempo característica para cargar el condensador. Es la escala de tiempo para la descarga de un condensador, es decir, si un condensador cargado (con voltaje V) está conectado directamente a un resistor para formar un circuito cerrado (correspondiente a la sustitución de la fuente de tensión en la figura 1 mediante un cable corto), entonces la corriente que fluye a través del resistor otra vez seguirá ecuación 2.

Un análisis similar puede hacerse para una resistencia en serie de un inductor o un circuito de "RL" como se muestra en la figura 2. Sin embargo, el comportamiento de un inductor es opuesta a la de un condensador, en el sentido de que el inductor se realiza mejor en una frecuencia más baja (para estado estable actual el inductor actúa como un cable corto con poca resistencia), sino conductas mucho menos en una frecuencia más alta o en situación transitoria (porque un inductor siempre trata de oponerse a los cambios en su actual). Como resultado, la corriente (t) que fluiría en el circuito RL mostrado en la figura 2 , después de cerrar el interruptor en el tiempo t = 0 (o encender la fuente de voltaje a la salida de V) sería:

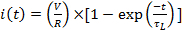(Ecuación 4)

donde,

(Ecuación 5)

que es la escala de tiempo característica general para la respuesta (aquí el cambio de corriente) del circuito RL con un cambio transitorio en una entrada (aquí el encendido de la fuente de tensión). Señalar, (t = 0) = 0, ya que inicialmente la corriente por el inductor (que es la misma corriente a través del resistor) no ha tenido oportunidad de cambiar desde su inicial valor cero (antes de encender la fuente de tensión), y el inductor trata de oponerse a cualquier cambio repentino en su actual. El circuito alcanza el estado estacionario, la corriente no cambia con el tiempo, entonces el inductor comporta como un cable corto y de hecho yo(t→∞) = V/R según ecuación 4. Este comportamiento (la corriente aumenta desde 0 y V/R aproxima exponencialmente) es representado en la figura 2y nota que está enfrente del comportamiento del circuito RC (ecuación 2 y figura 1, donde la corriente disminuye de V/R y decae exponencialmente a 0).

La dependencia exponencial de tiempo del circuito RC o RL está relacionado con la naturaleza disipativa de la resistencia. En contraste, un circuito "LC" donde un condensador está directamente conectado a un inductor con resistencia despreciable, como se muestra en la figura 3a, exhibe un comportamiento oscilatorio o "resonante". Figura 3a muestra un condensador, inicialmente cargado para tener un voltaje V, conectado a un inductor de la gota (con ninguna corriente a través de él al principio) en el tiempo t = 0. Se puede demostrar que la tensión subsecuente en el condensador (el mismo en el inductor) tendría la siguiente dependencia oscilatoria tiempo (sinusoidal):

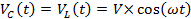(Ecuación 6)

donde,

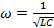(Ecuación 7)

es la "frecuencia de la oscilación" o "frecuencia resonante" (aquí, frecuencia se refiere a la frecuencia angular) del circuito del LC. La corriente por el inductor es:

(Ecuación 8)

El condensador descarga primero a través del inductor (V_C(t) disminuye y aumenta de i(t)). Cuando ωt llega a π/2, el condensador se descarga completamente (V_C = 0) y los flujos de corriente máxima en el inductor. Entonces el condensador se carga otra vez (por la corriente que fluye en el inductor) en la polaridad inversa (V_C(t) alcanza el -V cuando ωt π) y luego otra vez (totalmente descargadas cuando ωt alcanza 3π/2) y recargas a la polaridad original de V_C = V cuando ωt 2π. El ciclo se repite con el periodo de tiempo (t)

Tan un comportamiento oscilatorio, representado en la figura 3b, corresponde también al capacitor y el inductor de intercambio de energía electromagnética entre sí (un capacitor almacena energía en el campo eléctrico debido a la caída de tensión y un inductor almacenes de energía en el campo magnético debido a la corriente). En la situación ideal de la no resistencia (y por lo tanto no hay disipación) en el circuito, la oscilación puede continuar indefinidamente. En algunos la presencia de resistencia (disipación), por ejemplo en el circuito se muestra en la figura 3 c, también conocido como un circuito "RLC", tal una oscilación será amortiguada (si no hay ninguna fuente de alimentación externa), representado en la Figura 3dy después de una suficiente cantidad de tiempo tanto la tensión y corriente llegaría a cero.

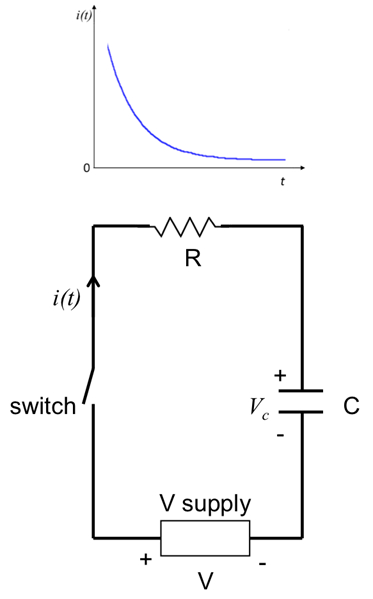
Figura 1: Diagrama que muestra un circuito RC con una resistencia (R) en serie con un condensador (C), conectado a una fuente de voltaje con un interruptor. Una corriente dependiente de tiempo representativo (dada por la ecuación 2) se representa por encima de la figura.

Figura 2: Diagrama que muestra un circuito RL, resistencia (R) en serie con un inductor (L), conectado a una fuente de voltaje con un interruptor. Una corriente dependiente de tiempo representativo (dada por la ecuación 4) se representa por encima de la figura.

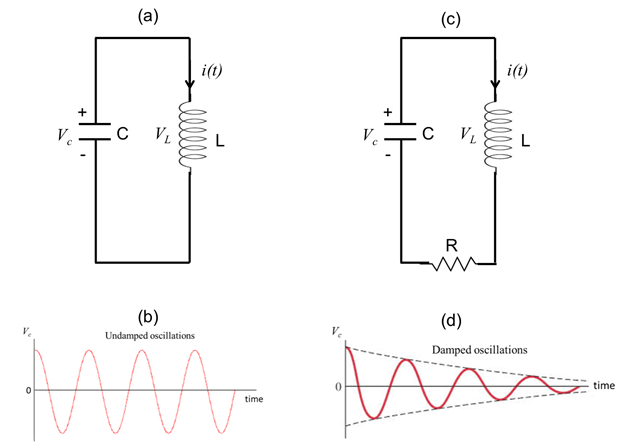
Figura 3: (a) diagrama que muestra un circuito LC con un inductor (L) conectado con un condensador (C) en un circuito cerrado. (b) un representante de voltaje dependiente de tiempo en el condensador, mostrando oscilación undamped (dado por la ecuación 6). (c) diagrama que muestra un circuito LC con una resistencia en serie (R), también conocido como un circuito RLC. (d) A voltaje dependiente de tiempo representativo en el condensador del circuito que se muestra en (c), que muestra una oscilación amortiguada.

1. utilizando un osciloscopio

1. Obtener un osciloscopio, un pequeño foco (con resistencia R de unos Ω), un interruptor y una fuente de voltaje DC (o alternativamente una batería V 1.5).
2. Conecte el circuito como se muestra en la figura 4, con el interruptor abierto. Las conexiones en este experimento pueden realizarse con cables, abrazaderas, o enchufes de plátano en la recepción de los puertos en los instrumentos.
3. Seleccione la escala vertical del osciloscopio a una gama que es cercano a 1 V. Seleccione la escala de tiempo del osciloscopio a una gama que es cercano a 1 s.
4. Cerrar el interruptor (así encender la bombilla de luz). Observar la bombilla, así como el rastro ("onda") en la pantalla del osciloscopio. El osciloscopio, conectado en paralelo a la bombilla, mida el voltaje a través de la bombilla, y este voltaje es proporcional a la corriente a través de la bombilla.
5. Ahora abra el interruptor otra vez (así apagar la bombilla). Observe otra vez la bombilla, así como el rastro ("onda") en la pantalla del osciloscopio.
6. Repita los pasos 1.4 y 1.5, si es necesario.

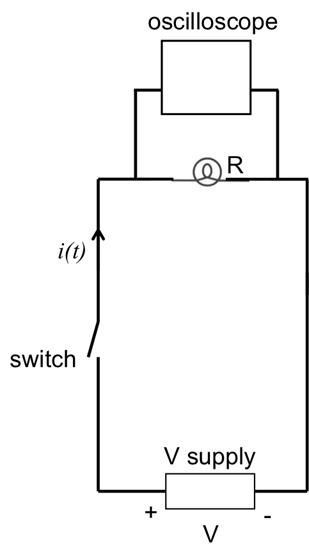
Figura 4 : Diagrama que muestra un foco conectado a una fuente de voltaje con un interruptor. Un osciloscopio está conectado en paralelo con la bombilla de luz para medir la tensión (proporcional a la corriente).

2. circuito RL

1. Obtener un inductor con inductancia L de 1 milihenry (mH).
2. Conectar el inductor en serie a la bombilla (con el osciloscopio conectado en paralelo con la bombilla de luz) y a la tensión de la fuente con un interruptor abierto, como se muestra en la figura 5a.
3. Cerrar el interruptor. Observar la bombilla, así como la forma de onda en el osciloscopio.
4. Abra el interruptor. Obtener otra bombilla (de la misma clase que la primera bombilla de luz) y conectarlo en paralelo con la primera bombilla de luz, como se muestra en la figura 5b.
5. Repita el paso 2.3 (cerrar el interruptor) y observar las bombillas y el osciloscopio.

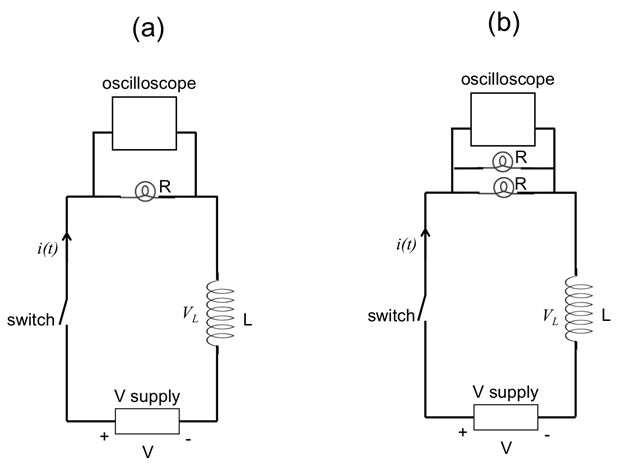
Figura 5 : Diagrama que muestra un circuito RL, con una bombilla (a) o dos focos de luz paralelo (b) actúa como resistor (R). Un osciloscopio está conectado en paralelo con las bombillas para medir el voltaje a través de las bombillas, proporcional a la corriente total.

3. circuito RC

1. Obtener un capacitor con una capacitancia de 1 faradio (F).
2. Conectar el condensador en serie con la bombilla (que está conectada en paralelo con el osciloscopio) y junto a la tensión de la fuente con el interruptor abierto, como se muestra en la Figura 6a. Esto corresponde al circuito similar que se muestra en la figura 5a conectado en el paso 2.2, excepto con el inductor sustituido por el condensador.
3. Cerrar el interruptor. Observar la bombilla, así como la forma de onda en el osciloscopio.
4. Abra el interruptor. Conecte la segunda bombilla en paralelo con la primera bombilla de luz, como se muestra en la figura 6b.
5. Repita el paso 3.3 (cerrar el interruptor) y observar las bombillas y el osciloscopio.

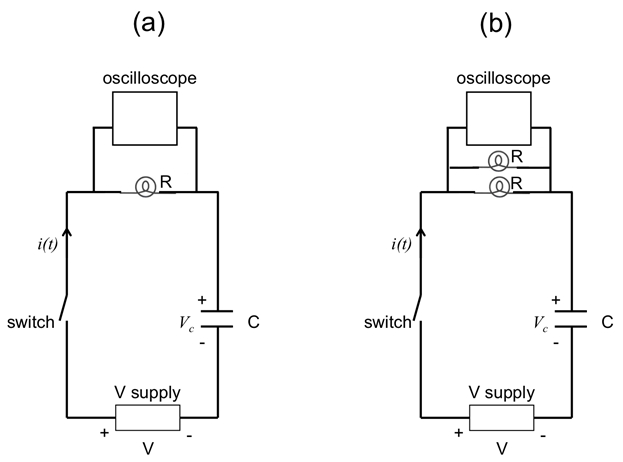
Figura 6 : Diagrama que muestra un circuito RC, con una bombilla (a) o dos focos de luz paralelo (b) actúa como resistor (R). Un osciloscopio está conectado en paralelo con las bombillas para medir el voltaje a través de las bombillas, proporcional a la corriente total.

3. circuito LC

1. Conectar un inductor 8 de mH en serie con otro interruptor abierto (interruptor #2) y, juntos, en paralelo a un condensador de 10 μF, como se muestra en la figura 7. Cerrar el interruptor #1 para tener el condensador cargado. No hay bombillas se utilizan en esta parte del experimento.
2. Conecte el osciloscopio en paralelo con el condensador, como se muestra en la figura 7.
3. Ahora abierto interruptor #1, luego cambiar enseguida también #2. Observar el osciloscopio.

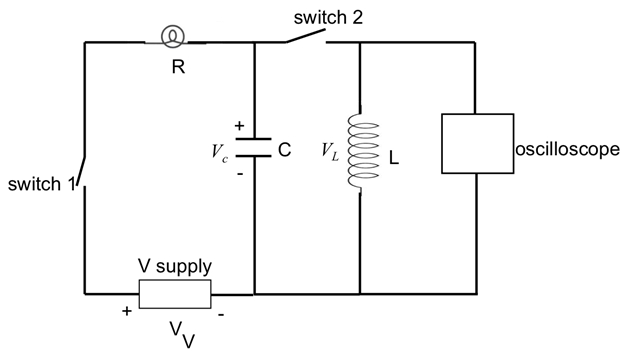
Figura 7 : Diagrama que muestra un inductor (L) con un interruptor conectado en paralelo a un condensador (C), que forma parte de un circuito RC serie estudiado en la figura 6. Ahora, el osciloscopio está conectado en paralelo con el inductor para medir su voltaje.

Para el paso 1, la voluntad de la bombilla "al instante" vuelta encendido y apagado cuando cierre (paso 1.4) y apertura (en el paso 1.5) el interruptor. Rastros de osciloscopio representativa se muestran en la figura 8.

Paso 2.3, después de cerrar el interruptor, se puede observar que lleva una pequeña pero notable cantidad de tiempo para la bombilla encender (en vez de al instante como en el paso 1). Cuando se utilizan dos bombillas paralelo (paso de 2.5), tarda un tiempo más largo para los focos de luz encender en comparación con el caso anterior (paso 2.3). Esto es porque los dos focos de luz paralelo da una menor resistencia (R) y así un largo tiempo constante τ_L = L/R para un circuito RL (nota que la constante de tiempo puede no ser exactamente dos veces como mucho porque los dos focos de luz no puede tener exactamente las mismas resistencias, y pueden existir otras resistencias no despreciable en el circuito). Representante de rastros en el osciloscopio para los dos casos se muestran en la figura 9. El tiempo de "encendido" escala mide en el osciloscopio es ~ ms y es consistente con el tiempo esperado constante τ_L basada en los valores de resistencia inductancia y foco de luz.

Paso 3.3, después de cerrar el interruptor, se puede observar que la bombilla se iluminará brevemente antes de morir hacia fuera. Cuando se utilizan dos bombillas paralelo (paso 3.5), tarda un tiempo más corto para las bombillas a morir hacia fuera en comparación con el caso anterior (paso 3.3). Esto es porque las dos bombillas en paralelo dan una menor resistencia (R), y así una RC más corto tiempo constante τ = RC. Representante de rastros en el osciloscopio para los dos casos se muestran en la figura 10. La escala de tiempo "encendido" de ~ 1 s es constante con el tiempo τ constante basado en los valores de resistencia capacitancia y foco de luz.

Paso 4.3, una tensión oscilatoria como los representados en la figura 3b, 3d se puede observar en el osciloscopio. Debido a la resistencia finita de los cables de conexión del circuito se puede observar cierta amortiguación de la oscilación. El período de la oscilación, del orden de milisegundos, es consistente con el período de oscilación de LC previsto (2π) basado en los valores de capacitancia y resistencia.

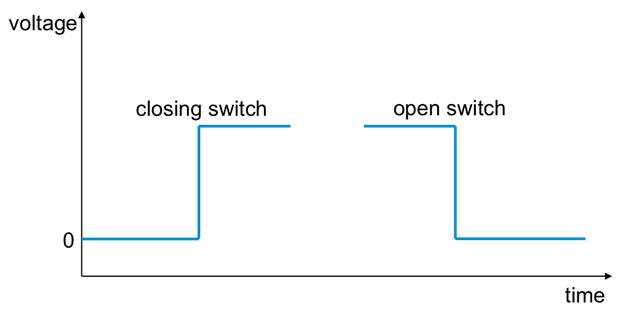
Figura 8 : Rastros de osciloscopio representativa (o "onda") que se puede observar en el experimento representado en la figura 4, cuando el interruptor está cerrado o abierto, medir el voltaje a través de un foco de luz directamente conectado a una fuente de voltaje.

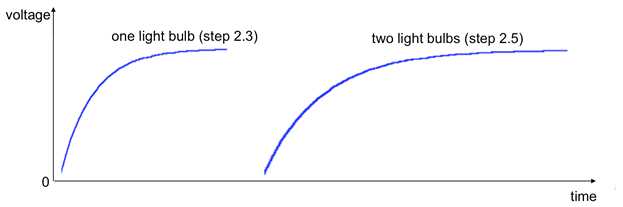
Figura 9 : Rastros de osciloscopio representativa (o "onda") que se puede observar cuando el interruptor está cerrado en el experimento representado en la figura 5, medir el voltaje a través de una bombilla conectada en serie de un inductor y una fuente de voltaje.

Figura 10 : Rastros de osciloscopio representativa (o "onda") que se puede observar cuando el interruptor está cerrado en el experimento representado en la figura 6, medir el voltaje a través de una bombilla conectada en serie de un condensador y una fuente de voltaje

En este experimento, hemos demostrado la respuesta dependiente del tiempo (exponencial da vuelta encendido y apagado) en circuitos RC o RL, y cómo cambiar la resistencia afecta la constante de tiempo. También hemos demostrado la respuesta oscilatoria en un circuito LC.

RC, circuitos RL y LC son bloques de edificio fundamentales en muchas aplicaciones de circuitos. Por ejemplo, circuitos RC y RL se utilizan como filtros (aprovechando el hecho de que los condensadores tienden a enviar señales de alta frecuencia pero bloquean señales de baja frecuencia, mientras que lo contrario es cierto para los inductores). También son útiles para el procesamiento de la señal eléctrica, por ejemplo, tomando la derivada o integral de una señal eléctrica. El circuito LC es un ejemplo simple de un "oscilador" electrónico o circuito de resonancia y es un componente común en los circuitos para amplificadores, radio sintonía, etc.

El autor del experimento agradece la ayuda de Gary Hudson para la preparación de material y Chuanhsun Li para la demostración de los pasos en el video.