磁場下における電荷

ソース: アンドリュー ダフィー博士は、物理学教室、ボストン大学、ボストン、マサチューセッツ

この実験は、^{彼は電子の質量電荷比を測定した、19 世紀}の終わりに j. j. トムソンの有名な実験を複製します。ロバート ・ ミリカンの油滴実験数年後電子の電荷の値を生成すると組み合わせると、実験では、電子のための重要なパラメーターであるの質量と電子の電荷の両方の最初の時間を探して、科学者が有効になります。

トムソン質量別々 に電子の電荷量や電子を測定することができませんでしたが、その比率を見つけることができました。このデモのも同じです。ここで、電子の電荷の大きさの値を検索することができるという利点があるが(e) と今両方知られている正確に (m_e)、電子の質量。

この実験で (真空管) の中の電子の磁気フィールド ビーム実験者のコントロールです。重要な概念の 1 つは、磁場が運動する電荷に力を適用できることです。充電速度を持っている場合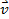磁気フィールドが、 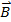、力の大きさによって与えられます。

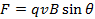(関係式 1)

qある電荷とθの大きさは、速度と磁場の間の角度です。罪のθ要因のため力は最大速度と磁場は、互いに垂直な速度と、フィールドが互いに平行に力がないと。

この力に方向があります。力の方向は速度と磁場によって定義される平面に垂直な (言い換えれば、力は速度と磁場の両方に対して垂直な)。力の正確な方向は右手の法則により決定することができます。右手の法則の 1 つのバージョンは次のとおりです。

右手を使用して、速度の方向に指を指します。

(並列のコンポーネントを生成力ない) 速度に垂直な磁場のコンポーネントについて考えます。磁場の垂直コンポーネントの方向に直面している手のひらまで、手を回転速度の方向に指を維持します。

親指を突き出します。限り、電荷は肯定的な親指移動電荷に及ぼす磁場によって適用されるフォースの方向に指摘しておきます。

電荷が負の場合、力は方法に反対の方向に親指ポイントです。

力は速度に垂直な、力は、粒子をスピードアップすることも、それを遅くことも。力を行うことができます、速度の方向を変更します。結果、速度と磁場は、互いに垂直な特殊なケースで、荷電粒子に円形のパスは、一定の速度で円の旅が続くことです。これ意味する求心性加速加速とニュートンの第 2 法則を適用ことができます等速円運動の定義です。

この場合。

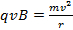(式 2)

これは運動する電荷の電荷質量比の式を見つけるに並べ替えることができます。

(式 3)

導出のための方程式の両側が乗します。

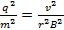(関係式 4)

再整理します。

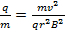(式 5)

これが、右側にある分子では電荷粒子の運動エネルギーを半分に奇妙なことのようになります。実験では、電子はVの電位差を残りから加速されるが、磁場に入る前に運動エネルギーを得る。省エネのアイデアを適用します。

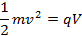
だから

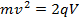(関係式 6)

電荷・質量方程式の結果に挿入します。

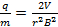(関係式 7)

だから単に 3 つの情報、すなわち、加速電圧、magnetic field の強さと荷電粒子の循環経路の半径を知ることによって、実験では、質量電荷比を見つけることが。

加速電圧Vが設定されて高電圧電源のスライダーは、電圧を読み取りに使用することができますメートルを供給します。

磁場Bは電流が流れてコイル、チューブの各側に 1 つのコイルのペアが生成されます。現在の私はデジタル電流計が読んで、特定のコイルの磁気フィールドを作成します。

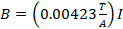(関係式 8)

ビームの軌道までの半径は管内 (図 1) 二次元 XY スケールから見つけることができます。(X, Y) 座標を持つポイント G を電子ビームが通過するまで、コイルの電流を調整します。X と Y の値は、管の内部のスケールを簡単に読むことができます。その後、直角三角形に図 1に示すように、サイド OE、R Y の長さを有し側 EG X. 適用ピタゴラスの定理の結果の長さ

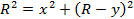(式 9)

この方程式の研究結果。

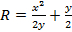(関係式 10)

これは、電荷質量比を決定するために必要なすべての情報です。

図 1: 電子ビームの幾何学の図。右に左に移動、電子入力 F 点における磁場 = (0, 0)、G 点を通過する円形のパスに磁場による偏向は、(X, Y) を =。調節可能な磁場は、管の両側に 1 つ (ヘルムホルツ コイルとして知られている)、2 つのコイルによって作成されます。この写真の magnetic field の方向ページからが、ビームが曲がるので、フィールドを取り消すことができますの代わりにダウン。円形のパスの中心は点 o. です。半径Rを決定することができますから、直角三角形が表示されます。

1. 地球の Magnetic Field を補う

1. この実験では 2 つの独立した回路があることに注意してください。
   1. 磁気フィールド (図 2) を作成するコイルに電流を供給します。現在はロータリー ダイヤルによって設定され回路にはにより、測定する電流デジタル電流計が含まれています。二重双極双投スイッチを使用して、反転磁場コイルに流れる電流の方向を逆にします。
   2. 第 2 の回路 (図 3) は、電子管を実行します。加速電圧を設定する高電圧供給があるし、6.3 V の交互になる信号をフィラメントに接続します。電子はフィラメントをゆで、加速電圧により加速され、いくつかの意味で、です。
2. 第 2 の回路では、高電圧電源、フィラメントを有効にするをオンに。管の内部にスイッチの光は、白熱フィラメントです。
3. 約 2,000 V の高電圧を徐々 に上げます。管内は電子ビームによって当られている、画面の部分は青、電子ビームの可視化グローする必要があります。
   1. 電子が青 - このわけメモ画面上のコーティングは蓄光と青色の輝きを放つこのコーティングの原子は、電子が通電。
4. 均一な磁場を作るコイルを流れる電流を調整します。現在の上下調節、ビームのパスを変更します。現在、グリッド上の (X, Y) 特定のポイントでビームを渡すを調整します。その点を通過するビームに必要な電流の大きさのメモしておきます。
5. 逆に電流が逆方向にビームを曲線し、ポイント (X、−Y) を通過するビームまで電流を調整する (元の点のミラー イメージ)。また、その特定のポイントを通過するビームに必要な電流の大きさのメモしておきます。
6. 2 つの電流の大きさが異なるかを確認してください。電子ビームは地球の磁場に平行に配置するチューブが起こらなければ、現在は一方向で、現在は、他の方向でそれから減算するときに、地球のフィールドがコイルのフィールドに追加します。
7. 実験中平均 2 つの電流、ビームを持っている必要な電流の大きさを通過 (X, Y) 特定のポイント、グリッド上と X (−Y)、地球の磁場の効果を削除するミラー イメージのポイントを通過するために必要な現在。

図 2: ヘルムホルツ コイルの回路図です。ヘルムホルツ コイルによって作成される magnetic field の強さはそれらを通る電流に比例します。調整可能な電源でコイルに流れる電流は、デジタル電流計によって測定されます。ダブル スイッチの目的は、簡単に磁場の方向を反転するコイルを通過する電流の方向を逆にすることです。各コイルに 2 つの接続、マークされているに注意してください A と Z、および 2 台の Z は、コイル磁場とは反対の方向の同じ方向で生産していることを確保するため一緒に接続必要があります。

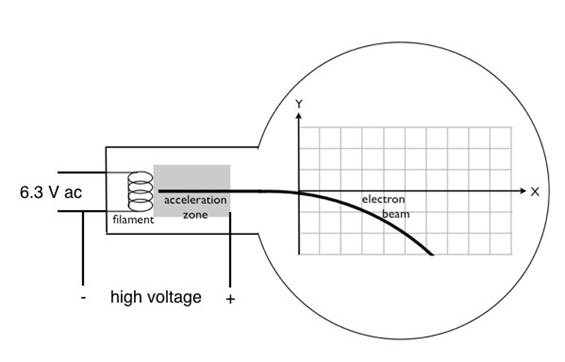
図 3: 電子管を実行するための回路図です。電子の源である白熱フィラメントは、6.3 V 交流電源によって実行されます。(約 2,000-3,000 V DC) 正の高電圧信号は加速ゾーンの右側の電極に接続されている高電圧信号の負の側面が、フィラメントの片側にも接続されているに注意してください。これは左から右へ電子を加速加速ゾーンの左監督大きな電界を生成します。

2. データ コレクション特定の (X, Y) と (X − Y) の組み合わせ

1. 管は高価で、やや壊れやすいことに注意してください。加速電圧 V 3,500 を超えるし、測定が取られていないときゼロに加速電圧をオンにしません。
2. この実験では、記録データは、それぞれ異なる加速電圧と同じ (X, Y) と (X, −Y) の 5 つのセットの組み合わせです。
3. 加速電圧を増加させると電子は速く移動、彼らは限り、曲げていない、したがって、コイルからの磁界が画面の同じポイントを通過するビームを持っている増加する必要がありますに注意してください。特定の (X, Y) を選択し、(X, −Y) 実験のこの部分に使用するポイント。ビームのパスの対応する半径を計算するのに方程式 10を使用します。
4. 特定の加速電圧の (X, Y) 選択した点を通過するビームに必要な電流の大きさを記録します。逆に、現在とミラー イメージのポイント (X, −Y) を通過するビームに必要な電流の大きさを記録します。
5. 地球の磁場の影響を除去する 2 つの電流の平均値します。
6. 式 8の現在の平均を使用して、磁場の強度を計算します。
7. 電子の電荷質量比の大きさを計算するのに加速電圧、半径、および磁場の値を使用します。
8. 新しい加速電圧を選択し、手順 2.3 2.7 を繰り返します。5 組のデータが収集されるまでこれを行うに進みます。
9. 電子の平均質量電荷比の大きさを計算します。

3 特定の加速電圧のデータ収集

1. 5 つのより多くのデータセットを収集します。今回は、加速電圧を一定に保つ、変更 (X, Y) と (X, −Y) ビームが通過点。データを記録します。
2. 電子の平均質量電荷比の大きさを計算します。
3. セクション 2、3、および状態実験における誤差の原因から 2 つの平均電荷質量比の平均値します。

セクション 2 の代表的な結果は、表 1で見ることができます。これらの値は、10^-11 C/kg x 1.717 の平均電荷質量比を与えます。電子の電荷は負値なので、その比率の大きさであることに注意してください。

セクション 3 の代表的な結果は、表 1で見ることができます。これらの値は、10^-11 C/kg x 1.677 の平均電荷質量比を与えます。再度、これ電子の電荷は負値なので、その比率の大きさでは。

質量電荷比の大きさの 2 つの値を平均し、3 つの有効数字に丸める 10^-11 C/kg × 1.70 の値を与えます。

この比率は、多くの有効数字の電子の質量と電子の電荷の値が知られているとして見てではなく正確に知られています。これらの知られている数量を使用して、それすることができます判断する電荷質量比の大きさ。

1.7588047 ± 0.0000049 C/kg

実験的に決定された価格が約 4% これより低いことに注意してください。実際には、系統誤差の表示は、承認済みの値より低い値のすべての 10 です。このような体系的なエラーの原因は、特に高電圧の値を与えるメーターで、メーターの 1 つになるでしょう。メーターは、実際の値よりも一貫して少し低かった測定値を与えた場合、それはひとりでにやや低い電荷質量比を説明できます。

地球の磁場の存在は 2 つの現在の値を平均することによって地球のフィールドの効果の実験を修正しましたので、エラーのソースではありません。しかし、方程式を導出の前提の 1 つは、コイルによって生成された磁場が均一だったです。フィールドは、無限長ソレノイドの中制服ですがエラーの可能性のあるソースになる可能性がありますので、この実験で使用される 2 つの有限コイル内部領域では完全に均一ではないです。

X = 7 cm Y = 1 cm R = 25 cm

加速電圧 (V)	を通過する電流の大きさ (X、 Y)	を通過する電流の大きさ (X、 −Y)	平均電流 (A)	磁場 (T)	e/m 比 (C/kg) x 1011
1,800	0.1537	0.1205	0.1371	0.0005799	1.713
2,000	0.1615	0.1242	0.14285	0.0006043	1.753
2,500	0.1800	0.1426	0.1613	0.0006823	1.718
3,000	0.1993	0.1571	0.1782	0.0007538	1.690
3,500	0.2136	0.1694	0.1915	0.0008100	1.707

表 1:特定の (X, Y) と (X, −Y) データ コレクションの塗りつぶされたテーブルの組み合わせ。

加速電圧 = 2,700 V

(Cm) x	Y (cm)	R (cm)	(X, Y) を通過する電流の大きさ	通過する電流の大きさ (X ・ Y)	平均電流 (A)	磁場 (T)	e/m 比 (C/kg) x 1011
7	1	25	0.1875	0.1500	0.16875	0.0007138	1.696
8	2	17	0.2702	0.2270	0.2486	0.001052	1.690
7	2	13.25	0.3378	0.2953	0.31655	0.001339	1.716
9	2	21.25	0.2166	0.1826	0.1996	0.0008443	1.678
10	1	50.5	0.1006	0.0710	0.0858	0.0003629	1.608

表 2:特定の加速電圧のデータ コレクションの塗りつぶされたテーブル。

この実験は、^{後半 19 世紀、} j ・ j ・ トムソンによって最初に実行はことを歴史的な観点から非常に重要な実験、電子の存在を示した。電子以来無数の電子デバイスに利用しました。

以下は円形またはスパイラルのパスで旅行している荷電粒子のいくつかのアプリケーションの一覧およびしたがって磁場で旅しています。

1) 地球の磁力線の周りスパイラル、極域におけるエネルギー荷電粒子による北極光 (オーロラ) とサザン ・ ライト (南天オーロラ) の形成。

2) A 陰極線管、LCD、LED、および血しょうスクリーンの新しい技術の前に、すべてのテレビのための基礎に使用されます。

3) A の質量分析計。いくつかの質量分析計は、磁場を利用した円形のパスにそれらの軌道を曲げることによってその質量に基づくイオン成分を分離します。パスの後に特定のイオンの半径がその質量に比例です。

4) 大型ハドロン衝突型加速器 (LHC)、有名な 27 km の円周楽器であるは、物理学者は最近なぜ粒子は質量を持っているために責任がある、ヒッグス粒子の存在を証明するために実験を行ったフランス、スイスの国境沿い地下に埋められます。