Carga Elétrica em um Campo Magnético

Fonte: Andrew Duffy, PhD, Departamento de Física, Universidade de Boston, Boston, MA

Este experimento duplica o famoso experimento de J.J. Thomson no final do século^XIX, no qual ele mediu a relação carga-massa do elétron. Em combinação com o experimento de gota de óleo de Robert A. Millikan alguns anos depois que produziu um valor para a carga do elétron, os experimentos permitiram que os cientistas encontrassem, pela primeira vez, tanto a massa quanto a carga do elétron, que são parâmetros-chave para o elétron.

Thomson não foi capaz de medir a carga eletrônica ou a massa eletrônica separadamente, mas ele foi capaz de encontrar sua razão. O mesmo vale para esta demonstração; embora aqui haja a vantagem de ser capaz de olhar para cima os valores para a magnitude da carga sobre o elétron(e) e a massa do elétron (m_e), que agora são ambos conhecidos precisamente.

Neste experimento, um feixe de elétrons (dentro de um tubo evacuado) e um campo magnético estão sob o controle do experimentador. Uma das ideias-chave é que um campo magnético pode aplicar uma força a uma carga móvel. Se a carga tem uma velocidade 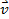e o campo magnético 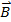é, então a magnitude da força é dada por:

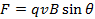(Equação 1)

onde q é a magnitude da carga e φ é o ângulo entre a velocidade e o campo magnético. Por causa do fatorpecado, a força é máxima quando a velocidade e o campo magnético são perpendiculares uns aos outros, e não há força quando a velocidade e o campo são paralelos um ao outro.

Esta força tem uma direção. A direção da força é perpendicular ao plano definido pela velocidade e pelo campo magnético (em outras palavras, a força é perpendicular tanto à velocidade quanto ao campo magnético). A direção exata da força pode ser determinada pela regra da direita. Uma versão da regra da direita é a seguinte:

Usando a mão direita, aponte os dedos na direção da velocidade.

Pense no componente do campo magnético que é perpendicular à velocidade (o componente paralelo não produz força). Mantendo os dedos na direção da velocidade, gire a mão até que a palma enfrente a direção do componente perpendicular do campo magnético.

Esia o polegar. Desde que a carga seja positiva, o polegar deve apontar na direção da força aplicada pelo campo magnético na carga móvel.

Se a carga for negativa, então a força está na direção oposta à forma como o polegar aponta.

Como a força é perpendicular à velocidade, a força não pode acelerar a partícula nem retardá-la. Tudo o que a força pode fazer é mudar a direção da velocidade. No caso especial de que a velocidade e o campo magnético são perpendiculares uns aos outros, o resultado é que a partícula carregada segue um caminho circular, viajando em um círculo em velocidade constante. Esta é a definição de movimento circular uniforme, o que significa que a segunda lei de Newton pode ser aplicada com a aceleração como a aceleração centrípeta.

Neste caso:

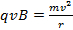(Equação 2)

Isso pode ser reorganizado para encontrar uma expressão para a relação carga-massa da carga móvel:

(Equação 3)

Para efeitos de derivação, ambos os lados da equação são quadrados:

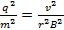(Equação 4)

Que reorganiza para:

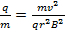(Equação 5)

Isso pode parecer uma coisa estranha de se fazer, mas note que no numerador do lado direito, há metade da energia cinética da partícula de cargas. No experimento, os elétrons ganham energia cinética, antes de entrar no campo magnético, sendo acelerados do resto através de uma diferença potencial, V. Aplicando ideias de conservação de energia:

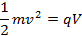
Então

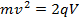(Equação 6)

Inserir isso na equação de carga em massa resulta em:

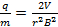(Equação 7)

Assim, no experimento, a relação carga-massa pode ser encontrada simplesmente conhecendo três pedaços de informação, ou seja, a tensão acelerada, a força do campo magnético e o raio do caminho circular seguido pelas partículas carregadas.

A tensão acelerada V é definida com um controle deslizante na fonte de alimentação de alta tensão, com um medidor que pode ser usado para ler a tensão.

O campo magnético B é produzido pela correnteza que atravessa um par de bobinas, com uma bobina em cada lado do tubo. A corrente é lida por um amímetro digital, e as bobinas específicas usadas criam um campo magnético de:

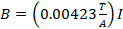(Equação 8)

O raio do caminho do feixe pode ser encontrado a partir de uma escala X-Y bidimensional dentro do tubo(Figura 1). A corrente nas bobinas é ajustada até que o feixe de elétrons passe pelo ponto G, que tem coordenadas de (X, Y). Os valores X e Y podem ser lidos facilmente fora da escala dentro do tubo. Em seguida, no triângulo de ângulo reto mostrado na Figura 1, o lado OE tem um comprimento de R-Y, e o EG lateral tem um comprimento de X. A aplicação do teorema de Pitagórico resulta em

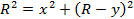(Equação 9)

Resolver esta equação para R resulta em:

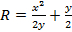  (Equação 10)

Esta é toda a informação necessária para determinar a relação carga-massa.

Figura 1: Diagrama da geometria para o feixe de elétrons. Os elétrons, viajando da esquerda para a direita, entram no campo magnético no ponto F = (0, 0) e são então desviados por um campo magnético em um caminho circular que passa pelo ponto G = (X, Y). O campo magnético ajustável é criado por duas bobinas (conhecidas como bobinas Helmholtz), uma em cada lado do tubo. A direção do campo magnético nesta imagem está fora da página, mas o campo pode ser invertido para que o feixe se incline para cima, em vez de para baixo. O centro do caminho circular está no ponto O. Um triângulo de ângulo reto é mostrado, a partir do qual o raio R pode ser determinado.

1. Compensação para o Campo Magnético da Terra

1. Observe que existem dois circuitos independentes neste experimento:
   1. Corrente de fornecimento para as bobinas que criam o campo magnético (Figura 2). A corrente é definida por um mostrador rotativo, e o circuito inclui um amímetro digital que permite medir a corrente. Um interruptor de duplo polo de duplo arremesso é usado para reverter a direção da corrente fornecida às bobinas, o que inverte o campo magnético.
   2. O segundo circuito (Figura 3)roda o tubo eletrônico. Há uma fonte de alta tensão, que define a tensão acelerada e um sinal alternado de 6,3 V conectado a um filamento. Os elétrons são, em certo sentido, fervidos do filamento e, em seguida, acelerados pela tensão acelerada.
2. No segundo circuito, ligue a fonte de alimentação de alta tensão para ligar o filamento. A luz que se liga dentro do tubo é o filamento brilhante.
3. Aumente gradualmente a alta tensão para cerca de 2.000 V. A parte da tela dentro do tubo, que está sendo atingida pelo feixe de elétrons, deve brilhar azul, tornando o feixe de elétrons visível.
   1. Note que isso não significa que os elétrons são azuis - o revestimento na tela é fosforescente e emite um brilho azul quando os átomos deste revestimento são energizados pelos elétrons.
4. Ajuste a corrente através das bobinas, que criam o campo magnético uniforme. À medida que a corrente é ajustada para cima ou para baixo, o caminho do feixe muda. Ajuste a corrente para passar o feixe através de um determinado ponto (X, Y) na grade. Anote a magnitude da corrente necessária para que a viga passe por esse ponto.
5. Inverta a corrente para curvar o feixe na direção oposta e ajuste a corrente até que o feixe passe pelo ponto (X, −Y) (a imagem do espelho do ponto original). Mais uma vez, anote a magnitude da corrente necessária para que a viga passe por esse ponto em particular.
6. Verifique se as magnitudes das duas correntes são diferentes. A menos que o tubo esteja alinhado para que o feixe de elétrons esteja paralelo ao campo magnético da Terra, o campo da Terra adiciona ao campo das bobinas quando a corrente está em uma direção e subtrai dele quando a corrente está na outra direção.
7. Ao longo do experimento, média das magnitudes das duas correntes, a corrente necessária para que o feixe passasse por um determinado ponto (X, Y) na grade, e a corrente necessária para passar pelo ponto de imagem espelhada (X, −Y), para remover o efeito do campo magnético da Terra.

Figura 2: Diagrama de circuito para as bobinas helmholtz. A força do campo magnético criado pelas bobinas Helmholtz é proporcional à corrente que passa por elas. A corrente fornecida às bobinas pela fonte de alimentação ajustável é medida pelo amímetro digital. O objetivo do interruptor duplo é facilmente inverter a direção da corrente que passa pelas bobinas, o que inverte a direção do campo magnético. Observe que as duas conexões de cada bobina estão marcadas A e Z, e as duas Z devem ser conectadas juntas para garantir que as bobinas estejam produzindo campos magnéticos na mesma direção, e não em direções opostas.

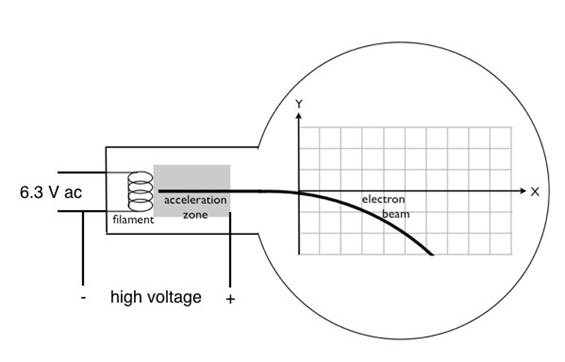
Figura 3: Diagrama de circuito para a execução do tubo de elétrons. O filamento brilhante que é a fonte dos elétrons é executado por uma fonte de corrente alternada de 6,3 V. Observe que o lado negativo do sinal de alta tensão também está conectado a um lado do filamento, enquanto o sinal positivo de alta tensão (na ordem de 2.000-3.000 V DC) está conectado a um eletrodo no lado direito da zona de aceleração. Isso produz um grande campo elétrico direcionado à esquerda na zona de aceleração, acelerando os elétrons da esquerda para a direita.

2. Coleta de dados para uma combinação particular (X, Y) e (X, − Y)

1. Note que os tubos são caros e um pouco frágeis. Não exceda 3.500 V para a tensão acelerada e gire a tensão acelerada para zero quando as medidas não estiverem sendo tomadas.
2. Nesta parte do experimento, registo cinco conjuntos de dados, cada um com uma tensão acelerada diferente com a mesma combinação (X, Y) e (X, −Y).
3. Note que à medida que a tensão acelerada aumenta e os elétrons viajam mais rápido, eles não dobram tanto, e assim, o campo magnético das bobinas precisa ser aumentado para que o feixe passe pelo mesmo ponto na tela. Escolha um determinado ponto (X, Y) e (X, −Y) para usar nesta parte do experimento. Use a Equação 10 para calcular o raio correspondente do caminho do feixe.
4. Para uma tensão acelerada particular, registo a magnitude da corrente necessária para que o feixe passe pelo ponto escolhido (X, Y). Inverta a corrente e regise a magnitude da corrente necessária para que o feixe passe pelo ponto de imagem do espelho (X, −Y).
5. Média das duas correntes para remover a influência do campo magnético da Terra.
6. Use a corrente média na Equação 8 para calcular a força do campo magnético.
7. Use os valores da tensão acelerada, raio e campo magnético para calcular a magnitude da relação carga-massa do elétron.
8. Escolha uma nova tensão acelerada e repita as etapas 2.3-2.7. Continue a fazer isso até que cinco conjuntos de dados tenham sido coletados.
9. Calcule a magnitude da relação carga-massa média para o elétron.

3. Coleta de dados para uma tensão acelerada particular

1. Colete mais cinco conjuntos de dados. Desta vez, mantenha a tensão acelerada constante e altere os pontos (X, Y) e (X, −Y) pelos que o feixe passa. Regisso.
2. Calcule a magnitude da relação carga-massa média para o elétron.
3. Em média, as duas relações médias de carga/massa determinadas da Seção 2 e 3, e afirmam possíveis fontes de erro no experimento.

Os resultados representativos da Seção 2 podem ser vistos na Tabela 1. Esses valores dão uma relação carga-massa média de 1,717 x 10^-11 C/kg. Note que essa é a magnitude da razão, porque a carga do elétron é um valor negativo.

Os resultados representativos da Seção 3 podem ser vistos na Tabela 1. Esses valores dão uma relação carga-massa média de 1,677 x 10^-11 C/kg. Novamente, esta é a magnitude da razão, porque a carga do elétron é um valor negativo.

A média dos dois valores da magnitude da relação carga-massa e arredondamento para três números significativos dá um valor de 1,70 x 10^-11 C/kg.

Essa razão é conhecida com bastante precisão, visto que o valor da carga do elétron e a massa do elétron de muitas figuras significativas é conhecido. Usando essas quantidades conhecidas, pode-se determinar que a magnitude da relação carga-massa é:

1,7588047 ± 0,0000049 C/kg

Note que o valor experimentalmente determinado é cerca de 4% menor do que este. Na verdade, todos os dez valores são inferiores ao valor aceito, o que é uma indicação de um erro sistemático. A fonte mais provável de tal erro sistemático seria em um dos medidores, particularmente no medidor que dá o valor da alta tensão. Se esse medidor fornecesse leituras consistentemente ligeiramente inferiores ao valor real, poderia explicar os valores ligeiramente baixos da relação carga-massa por si só.

A presença do campo magnético da Terra não é uma fonte de erro, porque o experimento corrigiu para o efeito do campo da Terra, fazendo uma média dos dois valores atuais. No entanto, uma das suposições em derivar a equação foi que o campo magnético produzido pelas bobinas é uniforme. O campo é uniforme dentro de um solenoide infinitamente longo, mas não é perfeitamente uniforme na região dentro das duas bobinas finitas usadas neste experimento, de modo que poderia ser uma possível fonte de erro.

X = 7 cm Y = 1 cm R = 25 cm

Tensão acelerada (V)	Magnitude da corrente para passar (X, Y)	Magnitude da corrente para passar (X, −Y)	Corrente média (A)	Campo magnético (T)	e/m razão (C/kg) x 1011
1,800	0.1537	0.1205	0.1371	0.0005799	1.713
2,000	0.1615	0.1242	0.14285	0.0006043	1.753
2,500	0.1800	0.1426	0.1613	0.0006823	1.718
3,000	0.1993	0.1571	0.1782	0.0007538	1.690
3,500	0.2136	0.1694	0.1915	0.0008100	1.707

Tabela 1: Uma tabela preenchida da coleta de dados para uma combinação específica (X, Y) e (X, −Y).

Tensão acelerada = 2.700 V

X (cm)	Y (cm)	R (cm)	Magnitude da corrente para passar (X,Y)	Magnitude da corrente para passar (X,-Y)	Corrente média (A)	Campo magnético (T)	e/m razão (C/kg) x 1011
7	1	25	0.1875	0.1500	0.16875	0.0007138	1.696
8	2	17	0.2702	0.2270	0.2486	0.001052	1.690
7	2	13.25	0.3378	0.2953	0.31655	0.001339	1.716
9	2	21.25	0.2166	0.1826	0.1996	0.0008443	1.678
10	1	50.5	0.1006	0.0710	0.0858	0.0003629	1.608

Tabela 2: Uma tabela preenchida da coleta de dados para uma tensão acelerada específica.

Este experimento, realizado pela primeira vez por J.J. Thomson no final do século^XIX, demonstrou a existência do elétron, tornando-o um experimento tremendamente importante de uma perspectiva histórica. Elétrons foram explorados em inúmeros dispositivos eletrônicos.

A seguir está uma lista de algumas aplicações de partículas carregadas que estão viajando em caminhos circulares ou espiral, e assim estão viajando em um campo magnético:

1)A formação das Luzes do Norte (Aurora Boreal) e Luzes do Sul (Aurora Australis) por partículas carregadas que giram em torno das linhas de campo magnético da Terra e depositam sua energia nas regiões polares.

2)Um tubo de raios catódicos, que costumava ser a base para todas as televisões, antes das novas tecnologias de telas LCD, LED e plasma.

3)Um espectrômetro de massa. Alguns espectrômetros de massa separam íons baseados em sua massa, dobrando suas trajetórias em caminhos circulares usando um campo magnético. O raio do caminho seguido por um determinado íon é proporcional à sua massa.

4)O Grande Colisor de Hádrons (LHC), que é o famoso instrumento de circunferência de 27 km enterrado no subsolo ao longo da fronteira França-Suíça, onde físicos realizaram recentemente experimentos para provar a existência do bóson de Higgs, que é responsável por por que as partículas têm massa.