Carga eléctrica en un campo magnético

Fuente: Andrew Duffy, PhD, Departamento de física de la Universidad de Boston, Boston, MA

Este experimento duplica el experimento famoso de J.J. Thomson al final del^{siglo 19, en el que midió la relación carga a masa del electrón} . En combinación con el experimento de gota de aceite de Robert A. Millikan unos años más tarde que producen un valor para la carga del electrón, los experimentos permitieron a los científicos a encontrar, por primera vez, la masa y la carga del electrón, que son parámetros fundamentales para el electrón.

Thomson no fue capaz de medir la carga del electrón o electrón masa por separado, pero fue capaz de encontrar su relación. Lo mismo es válido para esta demostración; Aunque aquí existe la ventaja de poder ver los valores de la magnitud de la carga en electrón(e) y la masa del electrón (m_e), que ahora ambos conocen precisamente.

En este experimento, un haz de electrones (dentro de un tubo evacuado) y un campo magnético están bajo control del experimentador. Una de las ideas claves es que un campo magnético puede aplicar una fuerza a una carga en movimiento. Si la carga tiene una velocidad de 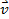y el campo magnético es 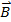, entonces la magnitud de la fuerza está dada por:

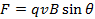(Ecuación 1)

donde q es la magnitud de la carga y θ es el ángulo entre la velocidad y el campo magnético. Por el factor deθ del pecado, la fuerza es máxima cuando la velocidad y campo magnético son perpendiculares uno al otro, y no hay ninguna fuerza cuando la velocidad y el campo son paralelas entre sí.

Esta fuerza tiene una dirección. La dirección de la fuerza es perpendicular al plano definido por la velocidad y el campo magnético (en otras palabras, la fuerza es perpendicular a la velocidad y el campo magnético). La dirección exacta de la fuerza puede determinarse por la regla derecha. Una versión de la regla derecha es el siguiente:

Con la mano derecha, punto de los dedos en la dirección de la velocidad.

Pensar en el componente del campo magnético que es perpendicular a la velocidad (el componente paralela no produce ninguna fuerza). Manteniendo los dedos en la dirección de la velocidad, gire la mano hasta que la palma enfrenta a la dirección de la componente perpendicular del campo magnético.

Sobresale el pulgar. Como la carga es positiva, el pulgar debe apuntar en la dirección de la fuerza aplicada por el campo magnético sobre la carga en movimiento.

Si la carga es negativa, entonces la fuerza es en sentido contrario a la forma de los puntos del dedo pulgar.

Porque la fuerza es perpendicular a la velocidad, la fuerza no puede acelerar la partícula ni retrasarlo. La fuerza puede hacer es cambiar la dirección de la velocidad. En el caso especial que la velocidad y el campo magnético son perpendiculares uno al otro, el resultado es que la partícula cargada sigue una trayectoria circular, viajando en un círculo a velocidad constante. Esta es la definición de movimiento circular uniforme, que significa segunda ley de Newton se puede aplicar con la aceleración como la aceleración centrípeta.

En este caso:

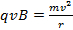(Ecuación 2)

Esto puede ordenarse para encontrar una expresión para la relación carga a masa de la carga en movimiento:

(Ecuación 3)

A los efectos de la derivación, ambos lados de la ecuación son cuadrados:

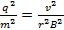(Ecuación 4)

Que vuelva a arregla:

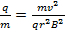(Ecuación 5)

Esto puede parecer una cosa extraña, pero tenga en cuenta que en el numerador del lado derecho, es mitad de la energía cinética de la partícula de cargos. En el experimento, los electrones ganan energía cinética, antes de entrar en el campo magnético, por ser acelerado desde el reposo mediante una diferencia de potencial, V. Aplicando ideas de conservación de la energía:

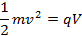
por lo tanto,

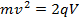(Ecuación 6)

Insertar los resultados de la ecuación de carga a masa en:

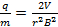(Ecuación 7)

Así que en el experimento, puede encontrarse la relación carga a masa simplemente conociendo tres piezas de información, es decir, el voltaje de aceleración, la fuerza del campo magnético y el radio de la trayectoria circular seguida por las partículas cargadas.

El voltaje de aceleración V se fija con un control deslizante en la alimentación de alto voltaje fuente, con un medidor que puede utilizarse para leer el voltaje.

El campo magnético B es producido por el funcionamiento actual a través de un par de bobinas, una bobina a cada lado del tubo. Actual es leído por un amperímetro digital, y las bobinas particular utilizadas crean un campo magnético de:

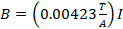(Ecuación 8)

El radio de la trayectoria del haz se puede encontrar desde una escala bidimensional de X-Y dentro del tubo (figura 1). La corriente en las bobinas se ajusta hasta que el haz de electrones pasa a través del punto G, que tiene coordenadas (X, Y). Los valores de X e Y se pueden leer fácilmente la escala dentro del tubo. Luego, en el triángulo rectángulo mostrado en la figura 1, lado OE tiene una longitud de R-Y y lado EG tiene una longitud de X. aplicando el teorema de Pitágoras resulta en

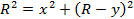(Ecuación 9)

Para resolver esta ecuación para R resultados en:

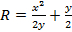(Ecuación 10)

Esta es toda la información necesaria para determinar la relación carga a masa.

Figura 1: Diagrama de la geometría para el haz de electrones. Los electrones, viajando de izquierda a derecha, entrar en el campo magnético en el punto F = (0, 0) y luego se desvía por un campo magnético en una trayectoria circular que pasa por el punto G = (X, Y). El campo magnético ajustable es creado por dos bobinas (conocidas como bobinas de Helmholtz), uno a cada lado del tubo. La dirección del campo magnético en esta foto es de la página, pero el campo se puede invertir para que la viga se dobla para arriba, en vez de hacia abajo. El centro de la trayectoria circular es en el punto O. Se muestra un triángulo rectángulo, de que el radio R puede ser determinado.

1. compensar el campo magnético de la tierra

1. Tenga en cuenta que existen dos circuitos independientes en este experimento:
   1. Suministrar corriente a las bobinas que crean el campo magnético ( figura 2). La corriente se establece por un dial rotatorio, y el circuito incluye un amperímetro digital que permite que la corriente a medir. Un interruptor de doble polo doble tiro se utiliza para invertir la dirección de la corriente suministrada a las bobinas, que invierte el campo magnético.
   2. Del segundo circuito ( figura 3) funciona el tubo del electrón. Hay una fuente de alta tensión, que establece el voltaje de aceleración y una señal alterna de 6.3 V conectados a un filamento. Electrones son, en cierto sentido, hervido apagado el filamento y luego acelerado por el voltaje de aceleración.
2. En el segundo circuito, encienda la fuente de alimentación de alto voltaje para encender el filamento. La luz que se enciende dentro del tubo es el filamento que brilla intensamente.
3. Poco a poco suba el alto voltaje a cerca de 2.000 V. La parte de la pantalla dentro del tubo, que está siendo golpeado por el haz de electrones, debe resplandor azul, haciendo visible el haz de electrones.
   1. Nota que esto no significa electrones son azules - la capa en la pantalla es fosforescente y emite un brillo azul cuando los átomos de esta capa son energizados por los electrones.
4. Ajustar la corriente a través de las bobinas, que crean el campo magnético uniforme. Como la corriente se ajusta hacia arriba o hacia abajo, cambia la trayectoria del haz. Ajustar la corriente para pasar el rayo a través de un punto particular (X, Y) en la red. Tome nota de la magnitud de la corriente que el rayo pase a través de ese punto.
5. Invertir la corriente para la viga en la dirección opuesta de la curva y ajustar la corriente hasta que el rayo pase por el punto (X, −Y) (la imagen especular del punto original). Una vez más, toma nota de la magnitud de la corriente que el rayo pase a través de ese punto particular.
6. Verifique si las magnitudes de las dos corrientes son diferentes. A menos que el tubo pasa a ser alineado el haz de electrones es paralelo al campo magnético de la tierra, campo de la tierra agrega al campo de las bobinas la corriente en una dirección y resta de ella cuando la corriente está en la otra dirección.
7. Durante todo el experimento, promedio las magnitudes de las dos corrientes, la corriente necesaria para que el rayo pasen por un punto particular (X, Y) de la red y la corriente necesaria para pasar por el espejo-imagen (X, −Y), para eliminar el efecto del campo magnético de la tierra.

Figura 2 : Diagrama del circuito para las bobinas de Helmholtz. La fuerza del campo magnético creado por las bobinas de Helmholtz es proporcional a la corriente que pasa a través de ellos. La corriente suministrada a las bobinas por la fuente de alimentación regulable se mide con el amperímetro digital. El propósito del interruptor doble es fácil invertir el sentido de la corriente que pasa por las bobinas, que invierte la dirección del campo magnético. Tenga en cuenta que las dos conexiones a cada bobina están marcadas A y Z y dos Z debe conectarse entre sí para asegurarse de que las bobinas están produciendo campos magnéticos en la misma dirección y no en direcciones opuestas.

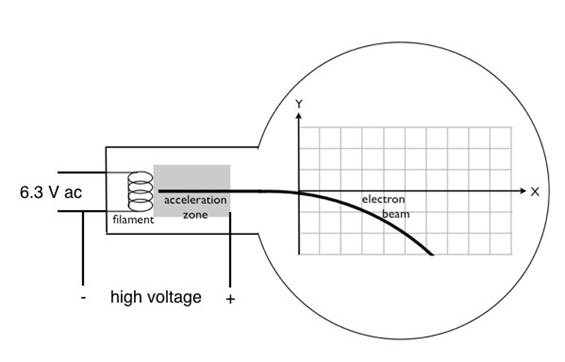
Figura 3 : Diagrama del circuito para correr el tubo del electrón. El filamento incandescente que es la fuente de los electrones está dirigido por una fuente de corriente alterna V 6.3. Tenga en cuenta que el lado negativo de la señal de alto voltaje está conectado también a un lado del filamento, mientras que la señal de positivo de alto voltaje (del orden de 2.000-3.000 V CC) está conectada a un electrodo en el lado derecho de la zona de aceleración. Esto produce un campo eléctrico dirigido de izquierda en la zona de aceleración, aceleración de los electrones de izquierda a derecha.

2. recopilación de un Particular (X, Y) y (X, − Y) combinación

1. Tenga en cuenta que los tubos son costosos y algo frágil. No exceda de 3.500 V para el voltaje de aceleración y convertir el voltaje de aceleración a cero cuando no se están tomando medidas.
2. En esta parte del experimento, grabar cinco conjuntos de datos, cada uno con un voltaje de aceleración diferentes con el mismo (X, Y) y (X, −Y) combinación.
3. Tenga en cuenta que aumenta el voltaje de aceleración y los electrones viajan más rápido, no se doblan tanto, y por lo tanto, el campo magnético de las bobinas tiene que aumentar para que el rayo pase por el mismo punto de la pantalla. Elegir una en particular (X, Y) y (X, −Y) punto a usar para esta parte del experimento. Utilice la ecuación 10 para calcular el correspondiente radio de trayectoria del haz.
4. Para un voltaje de aceleración particular, registrar la magnitud de la corriente necesaria para que el rayo pase por el punto elegido (X, Y). La corriente inversa y registrar la magnitud de la corriente necesaria para que el rayo pase por el punto imagen de espejo (X, −Y).
5. Promedio de las dos corrientes para eliminar la influencia del campo magnético de la tierra.
6. Utilizar la media actual en la ecuación 8 para calcular la fuerza del campo magnético.
7. Utilizar los valores de la tensión de aceleración, radio y campo magnético para calcular la magnitud de la relación carga a masa del electrón.
8. Elige un voltaje de aceleración de nuevo y repita los pasos 2.3-2.7. Continuar hacerlo hasta que se han recogido cinco conjuntos de datos.
9. Calcular la magnitud de la relación carga a masa promedio para el electrón.

3. recolección de un determinado voltaje de aceleración

1. Recoge cinco más conjuntos de datos. Esta vez, mantenga la aceleración constante de voltaje y (X, Y) y (X, −Y) puntos que el rayo pasa a través. Registrar los datos.
2. Calcular la magnitud de la relación carga a masa promedio para el electrón.
3. Promedio de los dos ratios de carga a masa promedio determinados de sección 2 y 3 y las fuentes posibles de error en el experimento de estado.

Representative results for Section 2 can be seen in Table 1. Those values give an average charge-to-mass ratio of 1.717 x 10^-11 C/kg. Note that that is the magnitude of the ratio, because the charge of the electron is a negative value.

Representative results for Section 3 can be seen in Table 1. Those values give an average charge-to-mass ratio of 1.677 x 10^-11 C/kg. Again, this is the magnitude of the ratio, because the charge of the electron is a negative value.

Averaging out the two values of the magnitude of the charge-to-mass ratio and rounding to three significant figures gives a value of 1.70 x 10^-11 C/kg.

This ratio is known rather precisely, seeing as the value of the charge of the electron and the mass of the electron of many significant figures is known. Using these known quantities, it can be determined that the magnitude of the charge-to-mass ratio is:

1.7588047 ± 0.0000049 C/kg

Note that the experimentally determined value is about 4% lower than this. In fact, all ten of the values are lower than the accepted value, which is an indication of a systematic error. The most likely source of such a systematic error would be in one of the meters, particularly in the meter that gives the value of the high voltage. If that meter gave readings that were consistently slightly lower than the actual value, it could explain the slightly low charge-to-mass ratio values all by itself.

The presence of Earth's magnetic field is not a source of error, because the experiment corrected for the effect of Earth's field by averaging the two current values. However, one of the assumptions in deriving the equation was that the magnetic field produced by the coils is uniform. The field is uniform inside an infinitely long solenoid, but is not perfectly uniform in the region inside the two finite coils used in this experiment, so that could be a possible source of error.

X = 7 cm    Y = 1 cm    R = 25 cm

Accelerating voltage (V)	Magnitude of current to pass through (X, Y)	Magnitude of current to pass through (X, −Y)	Average current (A)	Magnetic field (T)	e/m ratio (C/kg) x 1011
1,800	0.1537	0.1205	0.1371	0.0005799	1.713
2,000	0.1615	0.1242	0.14285	0.0006043	1.753
2,500	0.1800	0.1426	0.1613	0.0006823	1.718
3,000	0.1993	0.1571	0.1782	0.0007538	1.690
3,500	0.2136	0.1694	0.1915	0.0008100	1.707

Table 1: A filled-in table of the data collection for a particular (X, Y) and (X, −Y) combination.

Accelerating voltage = 2,700 V

X (cm)	Y (cm)	R (cm)	Magnitude of current to pass through (X,Y)	Magnitude of current to pass through (X,-Y)	Average current (A)	Magnetic field (T)	e/m ratio (C/kg) x 1011
7	1	25	0.1875	0.1500	0.16875	0.0007138	1.696
8	2	17	0.2702	0.2270	0.2486	0.001052	1.690
7	2	13.25	0.3378	0.2953	0.31655	0.001339	1.716
9	2	21.25	0.2166	0.1826	0.1996	0.0008443	1.678
10	1	50.5	0.1006	0.0710	0.0858	0.0003629	1.608

Table 2: A filled-in table of the data collection for a particular accelerating voltage.

Por primera vez por J.J. Thomson en los finales^del siglo 19, este experimento demostró la existencia del electrón, lo que es un experimento muy importante desde una perspectiva histórica. Electrones han sido explotados desde entonces en innumerables dispositivos electrónicos.

La siguiente es una lista de algunas aplicaciones de partículas cargadas que viajan en trayectorias circulares o en espiral, y así viaja en un campo magnético:

1) la formación de la aurora boreal (Aurora Borealis) y el Southern Lights (Aurora Australis) por partículas cargadas que espiral alrededor de las líneas de campo magnético de la tierra y depositan su energía en las regiones polares.

2) un cátodo – ray tubo, que solía ser la base para todos los televisores, antes de las nuevas tecnologías de pantallas LCD, LED y plasma.

Espectrómetro de masas A 3). Algunos espectrómetros de masas separan los iones basados en su masa doblando sus trayectorias en trayectorias circulares usando un campo magnético. El radio de la trayectoria de un ion particular es proporcional a su masa.

4) el Gran Colisionador de Hadrones (LHC), que es el instrumento de circunferencia de 27 km famoso enterrado subterráneo a lo largo de la frontera con Francia, Suiza, donde los físicos recientemente realizaban experimentos para probar la existencia del bosón de Higgs, que es responsable de por qué las partículas tienen masa.