Method Article
静電力によるスラストスタンドのトレーサブルキャリブレーション
要約
スラストスタンドの機械的特性のトレーサビリティ校正は、スラストのトレーサビリティ測定を確実にするための必須の前提条件です。ここでは、平行平板コンデンサによって発生する静電力によってスラストスタンドを較正する方法を説明します。
要約
マイクロスラスタは、低周波重力波検出や衛星形成、衛星間レーザー通信などに重要な用途があるため、トレーサビリティを持ってマイクロスラスタの推力を正確に測定する必要があります。スラストスタンドは、高解像度と大きな負荷の利点を備えた広く使用されているマイクロスラスト測定装置です。スラストスタンドの機械的特性のトレーサビリティ校正は、スラストのトレーサビリティ測定を確実にするための必須の前提条件です。この研究では、平行平板コンデンサを使用して、国際単位系(SI)にさかのぼることができるマイクロニュートンの静電力を生成することにより、スラストスタンドを較正しました。一定の静電容量勾配範囲は、シミュレーションと理論計算によって求められました。さらに、静電気力は、単純な原理、瞬時トリガー、およびトレーサビリティの利点を備えた標準電圧によって変更できます。このデバイスは、簡単な組み立てと短いトレーサビリティパスにより、マイクロニュートンスラストスタンドのトレーサビリティキャリブレーションに使用できます。
概要
マイクロスラスタは、超静的で超安定な宇宙実験プラットフォームが、低周波重力波検出で宇宙船の非保存的な力をリアルタイムで相殺するためのマイクロスラストを提供するために不可欠です。複雑な騒音環境下でのマイクロスラスターの推力を確実に測定することが、抗力のない制御を実現するための前提です。したがって、機械的応答モデルを確立するためには、スラストスタンドを高精度にキャリブレーションすることが不可欠です。スラストスタンドのキャリブレーション方法には、主に接触式と非接触式の2種類があります。
接触式キャリブレーション方法には、主にローププーリーウェイトシステム、インパクトハンマー、インパクト振り子などがあり、これらは従来のキャリブレーション方法です。2002年、Lakeら1 は、分銅と滑車を使用して、mNの範囲の較正力を適用しました。2006年、Polzinら2 も同様の自動システムを使用してスイングアームに垂直荷重をロードしましたが、力が10mN未満の場合、大きな誤差がありました。2004年、小泉ら3 は、力覚センサーが記録した力を衝突過程に積算することにより、発生した運動量を求めました。力センサの分解能は90mN、実効インパルスは20-80μN、100μNでの総誤差は2.6μNsでした。衝撃振り子は、機械的振動がキャリブレーションに深刻な影響を与えるため、大きなインパルス測定にのみ適しています。接触式校正方式は簡単に設定できますが、ドリフト誤差はゼロで、校正された力は一般に非接触式よりも大きくなります。したがって、マイクロフォーススラストスタンドのキャリブレーションには適していません。
非接触校正方法には、主にガス動態校正、電磁校正、静電校正などがあります。2002年、Jamisonら4 は、80 nN-1 μN、86.2 nNの推力(10.7%の誤差)、712 nNの推力(2%の誤差)の力範囲を生成するガス動的較正技術を開発しました。ガスダイナミックキャリブレーション技術は、nNおよびサブμNの力を確実に生成でき、実装が容易です。ただし、これは一種の間接キャリブレーション技術であり、国際単位系(SI)まで追跡することはできません。さらに、ガスの動的校正は真空中でのみ適しています。
電磁力はマイクロニュートンのオーダーと同じくらい小さくすることができ、電磁力と電流との間には良好な線形関係があり、再現性が良好です。Tangら5 は、永久磁石とコイルを用いた電磁校正技術を開発しました。測定範囲は10〜1000μN、校正力は10mN未満、310μNの校正信頼性は95%です。2013年、He et al.6 は、エアギャップ付きのリング電磁石と通電した銅線をキャリブレーションに使用しました。150μNの力の校正不確かさは4.17μNであり、校正力の範囲が大きく、スラストスタンドアームの変位に敏感ではなかったが、銅線電流が電磁石コアを磁化する問題があった。2019年、Lamら7 は、さまざまな磁石と市販のボイスコイルを使用して、さまざまな力を較正しました。構造はコンパクトで設置が簡単でした。また、力の範囲は30-23000μNと4桁と広く、静的力とパルス力の不確かさはそれぞれ18.47%と11.38%でした。ただし、スラストフレームのキャリブレーションでは、電磁力はSIにトレーサブルではありません。
静電力校正は、最も広く使用されている直接校正技術です。SeldenとKetsdever8 は、3%の誤差で数十マイクロニュートンの測定範囲を持つ較正装置として静電コーム(ESC)を使用しました。プレートの間隔が1mm変わると、力は2%変化しました。ただし、隣接する歯の間の距離は同じである必要があり、これは変位の小さいスラストスタンドにのみ適用できました。2012年、Pancottiら9 は、パルス範囲が0.01 mNs〜20 mNsの対称静電コームを設計しました。これにより、より大きな静電パルスを生成できます。ただし、複雑な構造と静電コームの損傷の容易さの欠点を解決する必要があります。
スラストスタンドを校正するための基準力としてトレーサブルなマイクロニュートン力を提供することが前提条件です。静電力は、計測研究所10,11,12で力をSIにトレースするために広く使用されています。静電力には、単純な原理、瞬時トリガー、および短いトレースパスという利点があります。本研究では、平行平板キャパシタを用いて、振り子推力スタンドの変位出力が加わった推力に比例する振り子推力スタンドを校正するための基準力として、静電力を発生させる役割を果たしました。推力と変位の比率がスラストスタンドの剛性です。コンデンサの静電容量勾配をキャリブレーションすることで、平行な2枚のプレートの姿勢を厳密に制御する必要がなくなりました。一定の静電容量勾配範囲は、シミュレーションと理論計算によって求められました。静電気力の範囲は、2つのプレートの間隔と面積によって調整でき、剛性の異なるスラストスタンドの効率的なキャリブレーションに適していました。
プロトコル
1. 実験的実現
- 図1に示すように、円形平行板コンデンサ、電動リニアステージ、スラストスタンド、キャパシタンスブリッジ、SMU機器、レーザー干渉計、その他のコンポーネントなど、すべてのシステムコンポーネントを収集します。
- プレートAを電動リニアステージに固定し、プレートBをスラストスタンドのアームに固定して、プレートAとBを平行にします。
注:プレートはアルミニウム合金の高精度研削によって処理されます。プレートAの直径は6cm、プレートBの直径は4cmですので、位置合わせ誤差は無視できます。 - 電動リニアステージ(分解能0.625μm)により、2枚のプレート間の距離 Dab を制御します。2つのプレートを完全にはめ込み、リニアステージを1mmの固定距離で引っ張ります。
- キャパシタンスブリッジ(分解能0.8aF、精度±5PPM)を2枚のプレートに接続し、プレート間隔の変更によるキャパシタンスCabの変動を測定します。
- 高電圧源測定ユニット(SMU)計器(Precision 0.012%, ±5 - ±1100 V)でコンデンサに標準電圧を印加し、制御可能な高精度静電気力を発生させます。
- レーザー干渉計(分解能10nm)をスラストスタンドのアームに直接向くように調整し、変位 x をリアルタイムで測定します。
2. キャパシタンスグラジエントのキャリブレーション
- 駆動プレートAは、電動リニアステージによってステップ長0.02mmでプレートBから離れた側に移動し、初期プレート間隔を1mmにします。
- プレート間隔の相対的な変化が0.12mmになるまで、各ステップの後にキャパシタンスブリッジによって2つの平行プレートのキャパシタンス値を測定します。
- 長さ0.02mmで逆ステップを開始し、初期位置に戻ります。
- 合計 5 回の反復可能な実験を実施します。
- 結果を当てはめて、平行平板コンデンサ dCab/ddab の静電容量勾配とプレート間隔の関係を求めます。
3. 推圧スタンドの静電力の口径測定
- コンデンサブリッジを平行プレートコンデンサから外します。
- 2つのプレートをSMU機器に接続し、2つのプレート間のスペースを1mmにします。
- 印加電圧が300Vになるまで、50Vのステップ値でコンデンサの両方のプレートで電圧Uをゼロから段階的に増やします。静電力Fは1/2U2(dCab/dd ab)に等しいです。
- レーザー干渉計を使用して、スラストスタンドアームの変位xをリアルタイムで測定します。Sampレーザー干渉計の周波数を50Hzに設定します。
- 印加電圧がゼロになるまで、コンデンサの両方のプレートで電圧 U を300Vからステップごとに50Vずつ減らします。
- 合計 5 回の反復可能な実験を実施します。
- 結果をあてはめて、静電力 F とスラストスタンドアームの変位xの関係を求めます。スラストスタンドの剛性 k をフックの法則( k = F / x)に従って計算します。
結果
プロトコルに従って、スラストスタンドの静電容量勾配と剛性が校正されます。静電力の原理を導入すべきです。外力Fの作用下で、2つの帯電したプレート間に相対運動Dabがあります。また、外力によるワークWは、コンデンサに蓄えられた電気エネルギーEに変換されます。電位差U、プレートQと静電容量Cの両方の電荷を求めることができる。2枚のプレート間に蓄積されたエネルギーは、式(1)に従って計算できます。外力による仕事は、式(2)に従って計算できます。
 (1)
(1)
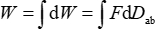 (2)
(2)
仮想作業13,14,15の原理に基づくと、WはEに等しい。
 (3)
(3)
外力により、2つのプレート間の距離 dz が変化し、その後
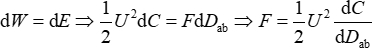 (4)
(4)
したがって、静電容量勾配を式(4)に基づいて較正する限り、電圧で静電力を計算することができます。2枚の円形金属板を使用して、平行板コンデンサーを形成しています。
図2 は、プレートAとプレートBの静電容量と変位の平均値のフィッティング曲線を示しています。静電容量勾配 dCab/dDab の平均は 6.2 pF/mm で、適合度は 0.9983 に達する可能性があります。したがって、式(4)によれば、平行平板コンデンサは1μN未満(電圧が17.96V未満の場合)のトレーサブルな力を生成でき、力の値の範囲は~0.279mNです。
図3A は、静電気力の変化によるスラストスタンドアームの変位変化を示しています。印加電圧が等距離に変化すると、各ステップの変位はますます大きくなります。電圧が増加し、電圧が減少すると、変位が対称的に変化することがわかります。 図3B は、スラストスタンドの変位と静電力の平均値のフィッティング曲線を示しています。スラストスタンドの剛性 k は式(5)で3.176N/m、繰り返し精度は0.0023N/mです。
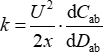 (5)
(5)
平行平板コンデンサの静電容量は、エッジ効果を無視した条件で式(6)と表すことができます。
 (6)
(6)
 (7)
(7)
Sはオーバーラップ領域、真空ε0 = 8.85 x 10-12 F / mの誘電率、および空気中の相対誘電率εr = 1です。プレートの間隔によって静電容量の勾配が変化することがわかります。ただし、プレートの間隔がほとんど変化しない場合、変化は非常に小さくなります。静電容量勾配は一定の値になる傾向があります。スラストスタンドキャリブレーションのmNマグニチュード標準力の要求に応じて、SMUの出力電圧が数百ボルトの場合、円形平行プレートコンデンサのプレート径はセンチメートルサイズ以内、距離Dabは式(1)および(2)を基準にしてミリメートルサイズ内にある必要があります。SMU機器の出力範囲は±5μV〜±1100Vであるため、プレートAとBの直径はそれぞれ6cmと4cmです。2つのプレート間の距離Dabは1mmです。
一定の静電容量勾配範囲を得るために、高電圧の平行平板コンデンサの電位分布、電界分布、静電容量、およびその他のパラメータを有限要素シミュレーションを使用して計算します。平行平板コンデンサの電位分布を 図4に示しますが、そのサイズは実際のデバイスと一致しています。マイクロニュートンの静電力の要求を満たすために、プレートの間隔は1mmに設定されています。 図5 は、平行プレートコンデンサの電界分布を示しています。矢印は電界の方向を表しており、高電圧から始まり、接地端子を指しています。平行平板コンデンサの静電容量は、平板の間隔を変えることでシミュレーションされます。ステップサイズは20μmで、1.2mmで終わります。 図6に示すように、プレート間隔が1mmから1.2mmのとき、静電容量勾配は9.81pF/mmの定数値です。式(4)によれば、静電容量勾配が一定の場合、静電力の大きさは印加電圧の2乗と線形の関係を持ちます。 図7 は、さまざまな電圧でシミュレートされた静電力を示しており、これは式(4)の導出に準拠しています。2つのプレート間の距離が1〜1.2 mmの場合、シミュレーション計算によれば、1〜1000μNの校正力を生成するには、電圧範囲は14.29〜451.57 Vです。
最後に、キャリブレーション結果の不確かさを以下で評価します。
1. 相対的不確実性のタイプA評価
不確実性の主な原因は、空気の乱れと地盤の振動です。ベッセル法によれば、5つの測定値の平均値を測定結果の最良の推定値として使用した場合、相対的な不確かさ urel(re)は0.0724%です。
2. 相対的不確実性のタイプB評価
ある。レーザー干渉計で測定された変位の相対的不確かさ
レーザー干渉計は、スラストスタンドの変位を測定するために使用されます。補償なしのレーザー干渉計の相対的な不確実性は0.005%であり、これは無視できます。
b.SMU機器による印加電圧の相対的不確かさ
SMU機器の相対的な不確実性は0.012%です。したがって、印加電圧 urel(U)によってもたらされる相対的な不確実性は0.012%です。
c. 静電容量勾配dCab/ddabの相対不確かさ
静電容量勾配 dCab/dd ab は、コンデンサ ブリッジで測定した静電容量を、電動リニア ステージで移動した距離に当てはめることによって得られます。容量性ブリッジの精度は5PPMで、その不確かさは無視できます。電動リニアステージの変位分解能は5μmです。その結果、dCab/dDabの相対不確かさは0.16%です。
3. 不確実性の拡大
不確かさの成分は、 表1にまとめられているように、互いに独立しています。相対的な不確かさは0.18%であるため、標準的な不確かさは0.0057N/mです。静電容量勾配によってもたらされる相対的な不確実性が最も寄与します。カバレッジ係数は3であるため、拡張不確かさは0.0171N /mです。
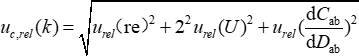 (8)
(8)
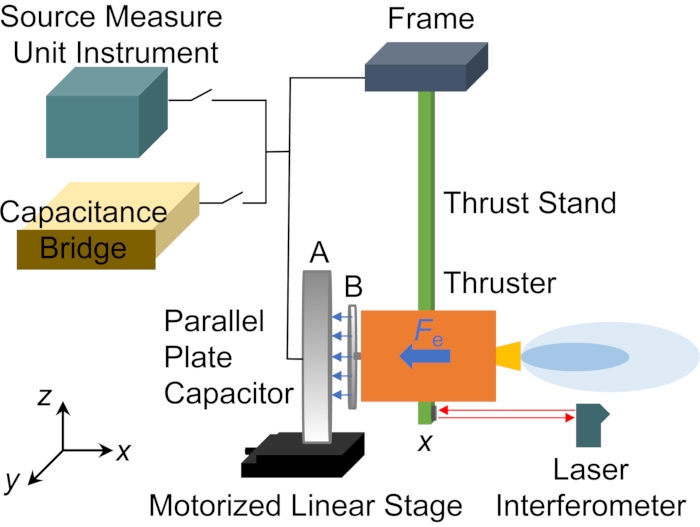
図1:平行平板コンデンサキャリブレーションスラストスタンドの概略図。 平行平板コンデンサは、スラストスタンドの校正の基準となる静電力を発生させました。 この図の拡大版を表示するには、ここをクリックしてください。

図2:平行平板コンデンサの静電容量とプレート間隔の関係。 フィッティングラインの傾きは静電容量勾配でした。 この図の拡大版を表示するには、ここをクリックしてください。

図3:スラストスタンドを校正する静電力 (A)スラストスタンドアームの変位。(B)スラストスタンドアームの静電気力と変位の関係。 この図の拡大版を表示するには、ここをクリックしてください。

図4:平行平板コンデンサの電位分布。 電位分布は均一でした。 この図の拡大版を表示するには、ここをクリックしてください。

図5:平行平板コンデンサの電界分布。 矢印は電界の方向を表しています。 この図の拡大版を表示するには、ここをクリックしてください。

図6:プレート間隔による静電容量変動のシミュレーション。 静電容量はプレートの間隔とともに減少しました。 この図の拡大版を表示するには、ここをクリックしてください。

図7:電圧による静電力のシミュレーション。 静電気力は、プレートコンデンサに印加される電圧とともに増加します。 この図の拡大版を表示するには、ここをクリックしてください。
| 不確実性の源 | 不確実性全体に占める割合(%) |
| 再現 | 0.07% |
| U | 0.01% |
| dcab/dd ab | 0.16% |
| 相対的な不確実性の組み合わせ | 0.18% |
表1:スラストスタンドのキャリブレーションの不確実性。
ディスカッション
このプロトコルでは、平行平板コンデンサを使用して、SIにトレースできるマイクロニュートンの静電力を発生させることにより、スラストスタンドを較正しました。すべてのステップで、静電容量勾配を正確に較正することが重要です。電動リニアステージは、この平行プレートコンデンサの初期プレート間隔を1mmに等しくし、プレートAを0.02mm刻みで移動させました。キャパシタンスブリッジは、キャパシタンス勾配を正確に較正するためのキャパシタンスを測定するために使用されました。静電容量勾配が式(4)に基づいて校正されている限り、電圧で静電力を計算することができます。
このプロトコルで静電力を発生させるための平行平板コンデンサは、範囲が狭くなります。電圧が高すぎると、一定に保つのが難しくなります。したがって、静電気力は、マイクロスラストスタンドのキャリブレーションにのみ適しています。
平行平板コンデンサには、単純な原理、瞬時トリガ、およびトレーサビリティという利点がありました。平行平板コンデンサの線形応答範囲は、シミュレーションと理論計算によって得られたため、スラストスタンドの機械的応答校正に適しています。電圧によって調整された基準力とレーザー干渉計によって測定された変位が得られ、スラストスタンドのキャリブレーションが完了しました。
平行平板コンデンサによって生成される静電力に基づくスラストスタンドのトレーサブルなキャリブレーションは、~0.279mNの範囲で1μN未満にすることができ、組み立てが簡単でトレーサブルな経路が短いという利点があります。スラストスタンドで測定した力をSIトレーサブル静電力にトレースし、測定精度を向上させました。この装置はマイクロ推力の測定、またマイクロニュートンのスラスターの設計そして開発に肯定的な影響を与える。
開示事項
著者は何も開示していません。
謝辞
この研究に資金を提供してくださった中国国家自然科学基金会(助成金第11772202号)に感謝します。
資料
| Name | Company | Catalog Number | Comments |
| Motorized linear stage | Zolix | TSA50-C | Resolution 0.625 μm |
| Capacitance bridge | Andeen-Hagerling | AH2550A | Resolution 0.8 aF, Accuracy ±5 PPM |
| High voltage source measure unit (SMU) instrument | Keithley | 2410 | Precision 0.012%, ±5 μV– ±1100 V |
| Laser interferometer | Renishaw | RLE10 | Resolution 10 nm |
| Circular parallel plate capacitor | Processed by high precision grinding | The plates are processed by high precision grinding of aluminum alloy. The diameter of plate A is 6 cm, and the diameter of plate B is 4 cm. | |
| Thrust stand | Processed by high precision grinding | Pendulum type thrust stand |
参考文献
- Lake, J. P., et al. Resonant Operation of a Micro-Newton Thrust Stand[C]. AIAA,38th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit. 3821, (2002).
- Polzin, K. A., Markusic, T. E., Stanojev, B. J., DeHoyos, A., Spaun, B. Thrust stand for electric propulsion performance evaluation. Review of Scientific Instruments. 77 (10), 105108(2008).
- Koizumi, H., Komurasaki, K., Arakawa, Y. Development of thrust stand for low impulse measurement from microthrusters. Review of Scientific Instruments. 75 (10), 3185(2004).
- Jamison, A. J., Ketsdever, A. D., Muntz, E. P. Gas dynamic calibration of a nano-Newton thrust stand. Review of Scientific Instruments. 73 (10), 3629(2002).
- Tang, H., Shi, C., Zhang, X., Zhang, Z., Cheng, J. Pulsed thrust measurements using electromagnetic calibration techniques. Review of Scientific Instruments. 82 (3), 035118(2011).
- He, Z., et al. Precision electromagnetic calibration technique for micro-Newton thrust stands. Review of Scientific Instruments. 84 (5), 055107(2013).
- Lam, J. K., Koay, S. C., Lim, C. H., Cheah, K. H. A voice coil based electromagnetic system for calibration of a sub-micronewton torsional thrust stand. Measurement. 131, 597-604 (2019).
- Selden, N. P., Ketsdever, A. D. Comparison of force balance calibration techniques for the nano-Newton range. Review of Scientific Instruments. 74 (12), 5249(2003).
- Pancotti, A. P., Gilpin, M., Hilario, M. S. Comparison of electrostatic fins with piezoelectric impact hammer techniques to extend impulse calibration range of a torsional thrust stand. Review of Scientific Instruments. 83 (3), 035109(2012).
- Zheng, Y., et al. Improving environmental noise suppression for micronewton force sensing based on electrostatic by injecting air damping. Review of Scientific Instruments. 85 (5), 055002(2014).
- Zheng, Y., et al. Elegant shadow making tiny force visible for water-walking arthropods and updated Archimedes' principle. Langmuir. 32 (41), 10522-10528 (2016).
- Zheng, Y., et al. The multi-position calibration of the stiffness for atomic-force microscope cantilevers based on vibration. Measurement Science and Technology. 26 (5), (2015).
- Song, L., et al. Highly sensitive, precise, and traceable measurement of force. Instrumentation Science & Technology. 44 (4), 386-400 (2016).
- Zheng, Y., Zhao, M., Sun, P., Song, L. Optimization of electrostatic force system based on Newton interpolation method. Journal of Sensors. 2018, 1-7 (2018).
- Zheng, Y., et al. A multiposition method of viscous measurement for small-volume samples with high viscous. IEEE Transactions on Instrumentation and Measurement. 69 (7), 4995-5001 (2020).
転載および許可
このJoVE論文のテキスト又は図を再利用するための許可を申請します
許可を申請さらに記事を探す
This article has been published
Video Coming Soon
Copyright © 2023 MyJoVE Corporation. All rights reserved