Method Article
通过静电力对推力架进行可追溯校准
摘要
推力台机械特性的可追溯性校准是确保推力测量可追溯性的重要前提。在这里,我们描述了如何通过平行板电容器产生的静电力来校准推力支架。
摘要
微型推进器在低频引力波探测、卫星形成和星间激光通信方面具有重要应用,因此需要精确测量具有可追溯性的微型推进器推力。推力架是一种应用广泛的微推力测量装置,具有分辨率高、载荷大等优点。推力台机械特性的可追溯性校准是确保推力测量可追溯性的重要前提。在这项研究中,使用平行板电容器通过产生微牛顿静电力来校准推力台,这可以追溯到国际单位制 (SI)。通过仿真和理论计算得到恒定电容梯度范围。此外,静电力可以通过标准电压来改变,具有原理简单、瞬时触发和可追溯性等优点。由于组装简单且可追溯性路径短,该装置可用于微牛顿推力台的可追溯性校准。
引言
微型推力器对于超静态和超稳定空间实验平台来说是必不可少的,在低频引力波探测中,提供微推力以实时抵消航天器上的非保守力。在复杂的噪声环境中可靠测量微型推进器的推力是实现无阻力控制的前提。因此,必须高精度校准推力台以建立机械响应模型。推力架的标定方法主要包括接触式和非接触式两种标定方法。
接触式标定方法主要包括绳索滑轮配重系统、冲击锤和冲击摆等传统标定方法。2002 年,Lake 等人1 使用砝码和滑轮施加 mN 范围内的校准力。2006 年,Polzin 等人2 也使用类似的自动系统将垂直载荷加载到摆臂中,但当力小于 10 mN 时,它会产生很大的误差。2004 年,Koizumi 等人 3 通过将力传感器记录的力整合到碰撞过程中来获得产生的动量。力传感器的分辨率为 90 mN,有效脉冲为 20-80 μNs,100 μNs 时总误差为 2.6 μNs。冲击摆仅适用于大脉冲测量,因为机械振动严重影响校准。接触式标定方法虽然设置简单,但存在零点漂移误差,标定力一般比非接触式方法大。因此,它不适合校准微力推力架。
非接触式校准方法主要包括气体动态校准、电磁校准和静电校准。2002 年,Jamison 等人4 开发了一种气体动态校准技术,该技术产生了 80 nN-1 μN 的力范围、86.2 nN 的推力(10.7% 的误差)和 712 nN 的推力(2% 的误差)。气体动力学校准技术可以可靠地产生 nN 和 sub-μN 力,并且易于实施。然而,它是一种间接校准技术,无法追溯到国际单位制 (SI)。此外,气体动态校准仅适用于真空。
电磁力可以小到微牛顿的数量级,并且电磁力与电流之间有很好的线性关系,具有良好的重复性。Tang 等人5 开发了一种使用永磁体和线圈的电磁校准技术。测量范围为 10-1000 μNs,校准力小于 10 mN,310 μN 的校准可靠性为 95%。2013 年,He et al.6 使用带气隙的环形电磁铁和通电铜线进行校准。150 μN 力的标定不确定度为 4.17 μN,标定力范围大,对推力架臂的位移不敏感,但存在铜线电流会磁化电磁铁芯的问题。2019 年,Lam 等人7 使用不同的磁铁和商用音圈来校准各种力。结构紧凑,易于安装。力范围较大,为30-23000 μN的四个数量级,静力和脉冲力的不确定度分别为18.47%和11.38%。然而,对于推力系的校准,电磁力无法追溯到 SI。
静电力校准是使用最广泛的直接校准技术。Selden 和 Ketsdever8 使用静电梳 (ESC) 作为校准装置,测量范围为数十微牛顿,误差为 3%。当板间距变化 1 mm 时,力变化了 2%。但是,相邻齿之间的距离应相同,这仅适用于小位移的推力台。2012 年,Pancotti 等人9 设计 了一种对称静电梳,其脉冲范围为 0.01 mNs-20 mNs,可以产生更大的静电脉冲。然而,静电梳结构复杂、易损坏的缺点有待解决。
提供可追踪的微牛顿力作为校准推力台的参考力是先决条件。静电力在计量研究所 10,11,12 中被广泛用于将力追溯到 SI。静电力具有原理简单、瞬时触发、追踪路径短等优点。在本研究中,平行板电容器产生静电力作为参考力,以校准摆锤推力架,其位移输出与施加的推力成正比。推力和位移的比值是推力架的刚度。通过校准电容器的电容梯度,无需严格控制两个平行板的姿态。通过仿真和理论计算得到恒定电容梯度范围。静电力范围可通过两块板的间距和面积进行调整,适用于不同刚度的推力台的高效标定。
研究方案
1. 实验实现
- 收集所有系统组件,包括圆形平行板电容器、电动线性平台、推力架、电容桥、SMU 仪器、激光干涉仪和其他组件,如图 1 所示。
- 将板 A 固定在电动线性平台上,将板 B 固定在推力架的臂上,使板 A 和 B 彼此平行。
注:板材采用铝合金高精度磨削加工而成。板 A 的直径为 6 cm,板 B 的直径为 4 cm,因此可以忽略对准误差。 - 通过电动线性平台(分辨率 0.625 μm)控制两块板之间的距离 Dab 。完全适合两块板,然后通过线性载物台拉动 1 mm 的固定距离。
- 将电容桥(分辨率 0.8 aF,精度 ±5 PPM)与两块板连接,以测量电容 Cab 随 板间距变化的变化。
- 通过高压源测量单元 (SMU) 仪器(精度 0.012%,±5 - ±1100 V)向电容器施加标准电压,以产生可控的高精度静电力。
- 调整激光干涉仪(分辨率 10 nm)使其直接面向推力架的臂,并实时测量位移 x 。
2. 电容梯度的校准
- 通过电动线性平台驱动板 A 以 0.02 mm 的步长移动到远离板 B 的一侧,并使初始板间距等于 1 mm。
- 每一步后通过电容桥测量两个平行板的电容值,直到板间距的相对变化为 0.12 mm。
- 以 0.02 mm 的长度开始反向步骤,以返回到初始位置。
- 总共进行 5 次可重复实验。
- 对结果进行拟合,得到电容梯度与平行板电容器 dCab/dDab 的极板间距之间的关系。
3. 推力台的静电力校准
- 断开电容器桥与平行板电容器的连接。
- 将两个板与 SMU 仪器连接,使两个板之间的间距等于 1 mm。
- 在电容器的两极板上以 50 V 的步长值逐步从零开始增加电压 U ,直到施加的电压为 300 V。静电力 F 等于 1/2U2(dCab/dDab)。
- 使用激光干涉仪实时测量推力支架臂的位移 x。将激光干涉仪的采样频率设置为 50 Hz。
- 在电容器的两极板上以 50 V 的步长值从 300 V 逐步降低电压 U ,直到施加的电压为零。
- 总共进行 5 次可重复实验。
- 拟合结果以获得静电力 F 与推力架臂的位移 x 之间的关系。根据胡克定律计算推力架的刚度 k,k = F/x。
结果
按照协议,校准推力台的电容梯度和刚度。应介绍静电力的原理。在外力 F 的作用下,两个带电板之间会有相对运动 Dab。此外,功 W 受外力作用,会转化为储存在电容器中的电能 E。可以获得电位差 U、极板 Q 的电荷和电容 C。两块板之间存储的能量可以根据方程(1)计算。外力所做的功可以根据方程(2)计算。
 (1)
(1)
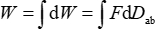 (2)
(2)
根据虚功 13,14,15 的原理,W 等于 E。
 (3)
(3)
外力改变两块板之间的距离 dz ,然后
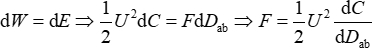 (4)
(4)
因此,只要根据方程 (4) 校准电容梯度,就可以通过电压计算静电力。两个圆形金属板用于形成一个平行板电容器。
图 2 显示了板 A 和板 B 的电容和位移平均值的拟合曲线。电容梯度 dCab/dDab 的平均值为 6.2 pF/mm,拟合优度可达 0.9983。因此,根据方程 (4),平行板电容器可以产生小于 1 μN 的可追踪力(只要电压小于 17.96 V),力值范围为 ~0.279 mN。
图 3A 显示了推力架臂的位移随静电力变化的变化。随着施加的电压等距变化,每个阶跃位移变得越来越大。可以看出,位移随着电压的增加和电压的降低而对称变化。 图 3B 显示了推力台位移和静电力的平均值的拟合曲线。根据方程 (5),推力台的刚度 k 为 3.176 N/m,重复精度为 0.0023 N/m。
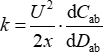 (5)
(5)
在忽略边缘效应的情况下,平行板电容器的电容可以描述为方程(6)。
 (6)
(6)
 (7)
(7)
S 是重叠面积、真空ε介电常数 0 = 8.85 x 10-12 F/m,以及空气中的相对介电常数 r = 1 ε。可以看出,电容梯度随板间距的变化而变化。但是,当板间距变化很小时,变化非常小。电容梯度趋于恒定值。根据推力台校准的 mN 幅度标准力的要求,当 SMU 的输出电压为几百伏时,圆形平行板电容器的板径应在厘米幅度以内,距离 Dab 应在毫米幅度内,基于方程 (1) 和 (2)。SMU 仪器的输出范围为 ±5 μV- ±1100 V。因此,板 A 和 B 的直径分别为 6 cm 和 4 cm。两块板之间的距离 Dab 为 1 mm。
为了获得恒定的电容梯度范围,采用有限元仿真计算了高压平行板电容器的电位分布、电场分布、电容等参数。平行板电容器的电位分布如图 4 所示,其尺寸与实际器件一致。为了满足微牛顿静电力的需求,极板间距设置为 1 mm。 图 5 显示了平行板电容器的电场分布。箭头表示电场的方向,从高压开始,指向接地端子。通过改变极板间距来模拟平行板电容器的电容。步长为 20 μm,终点为 1.2 mm。如图 6 所示,当板间距在 1 mm 和 1.2 mm 之间时,电容梯度为 9.81 pF/mm 的常数值。根据方程(4),当电容梯度为固定常数时,静电力的大小与外加电压的平方呈线性关系。 图 7 显示了不同电压下的模拟静电力,这与方程 (4) 的推导一致。当两板之间的距离为 1-1.2 mm 时,为了产生 1-1000 μN 的校准力,根据仿真计算,电压范围为 14.29-451.57 V。
最后,下面评估校准结果的不确定性。
1. 相对不确定性的 A 类评估
不确定性的主要来源是空气扰动和地面振动。根据贝塞尔方法,当使用五个测量值的平均值作为测量结果的最佳估计值时,相对不确定度 urel(re) 为 0.0724%。
2. 相对不确定度的 B 类评估
一个。激光干涉仪测量的位移的相对不确定度
激光干涉仪用于测量推力台的位移。无补偿激光干涉仪的相对不确定度为 0.005%,可以忽略不计。
b.SMU 仪器施加的电压的相对不确定度
SMU 仪器的相对不确定度为 0.012%。因此,由施加电压 urel(U) 引入的相对不确定度为 0.012%。
c. 电容梯度 dCab/dDab 的相对不确定度
电容梯度 dCab/dDab 是通过将电容器电桥测得的电容与电动线性平台移动的距离拟合而获得的。电容电桥的精度为 5 PPM,其不确定性可以忽略不计。电动线性平台的位移分辨率为 5 μm。因此,dCab/dDab 的相对不确定度为 0.16%。
3. 扩大的不确定性
不确定性分量彼此独立,如 表 1 所示。相对不确定度为 0.18%,因此标准不确定度为 0.0057 N/m。电容梯度引入的相对不确定性贡献最大。覆盖率因子为 3,因此扩展不确定度为 0.0171N /m。
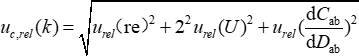 (8)
(8)
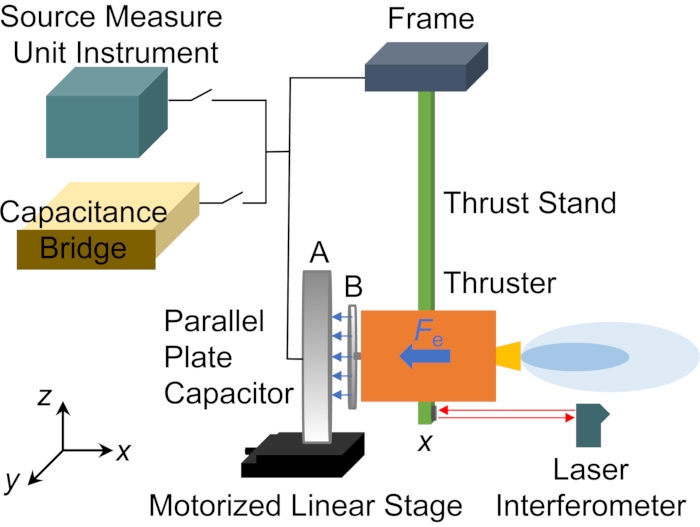
图 1:平行板电容器校准推力架的示意图。 平行板电容器产生静电力,作为校准止推台的参考。 请单击此处查看此图的较大版本。

图 2:平行板电容器的电容和极板间距之间的关系。 拟合线的斜率是电容梯度。 请单击此处查看此图的较大版本。

图 3:校准推力架的静电力。 (A) 推力架臂的位移。(B) 静电力与推力支架臂位移之间的关系。 请单击此处查看此图的较大版本。

图 4:平行板电容器的电位分布。 电位分布是均匀的。 请单击此处查看此图的较大版本。

图 5:平行板电容器中的电场分布。 箭头表示电场的方向。 请单击此处查看此图的较大版本。

图 6:电容随板间距变化的模拟。 电容随板间距的增加而减小。 请单击此处查看此图的较大版本。

图 7:静电力与电压的模拟。 静电力随着施加到板电容器上的电压而增加。 请单击此处查看此图的较大版本。
| 不确定性来源 | 对总不确定性的贡献 (%) |
| 重复性 | 0.07% |
| U | 0.01% |
| dCab/dDab | 0.16% |
| 综合相对不确定性 | 0.18% |
表 1:推力台校准的不确定性。
讨论
在该协议中,使用平行板电容器通过产生微牛顿静电力来校准推力台,该静电力可以追溯到 SI。所有步骤都必须精确校准电容梯度。电动线性平台使该平行板电容器的初始极板间距等于 1 mm,并以 0.02 mm 的步长移动极板 A。电容电桥用于测量电容,以精确校准电容梯度。只要根据方程 (4) 校准电容梯度,就可以通过电压计算静电力。
在该协议中,用于产生静电力的平行板电容器受到较小范围的限制。电压过高很难保持恒定。因此,静电力仅适用于校准微型推力台。
平行板电容器具有原理简单、瞬时触发、可追溯性等优点。通过仿真和理论计算得到平行板电容器的线性响应范围,使其适用于推力台的机械响应校准。得到电压调整的参考力和激光干涉仪测得的位移,完成推力台的标定。
基于平行板电容器产生的静电力,推力架的可溯源校准在 ~0.279 mN 范围内可以小于 1 μN,具有组装简单和可追溯路径短的优点。将推力台测得的力追溯到 SI 可追溯的静电力,以提高测量精度。该装置对微推力的测量以及微牛顿推进器的设计和开发具有积极影响。
披露声明
作者没有什么可披露的。
致谢
我们感谢中国国家自然科学基金(第 11772202 号)资助这项工作。
材料
| Name | Company | Catalog Number | Comments |
| Motorized linear stage | Zolix | TSA50-C | Resolution 0.625 μm |
| Capacitance bridge | Andeen-Hagerling | AH2550A | Resolution 0.8 aF, Accuracy ±5 PPM |
| High voltage source measure unit (SMU) instrument | Keithley | 2410 | Precision 0.012%, ±5 μV– ±1100 V |
| Laser interferometer | Renishaw | RLE10 | Resolution 10 nm |
| Circular parallel plate capacitor | Processed by high precision grinding | The plates are processed by high precision grinding of aluminum alloy. The diameter of plate A is 6 cm, and the diameter of plate B is 4 cm. | |
| Thrust stand | Processed by high precision grinding | Pendulum type thrust stand |
参考文献
- Lake, J. P., et al. Resonant Operation of a Micro-Newton Thrust Stand[C]. AIAA,38th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit. 3821, (2002).
- Polzin, K. A., Markusic, T. E., Stanojev, B. J., DeHoyos, A., Spaun, B. Thrust stand for electric propulsion performance evaluation. Review of Scientific Instruments. 77 (10), 105108 (2008).
- Koizumi, H., Komurasaki, K., Arakawa, Y. Development of thrust stand for low impulse measurement from microthrusters. Review of Scientific Instruments. 75 (10), 3185 (2004).
- Jamison, A. J., Ketsdever, A. D., Muntz, E. P. Gas dynamic calibration of a nano-Newton thrust stand. Review of Scientific Instruments. 73 (10), 3629 (2002).
- Tang, H., Shi, C., Zhang, X., Zhang, Z., Cheng, J. Pulsed thrust measurements using electromagnetic calibration techniques. Review of Scientific Instruments. 82 (3), 035118 (2011).
- He, Z., et al. Precision electromagnetic calibration technique for micro-Newton thrust stands. Review of Scientific Instruments. 84 (5), 055107 (2013).
- Lam, J. K., Koay, S. C., Lim, C. H., Cheah, K. H. A voice coil based electromagnetic system for calibration of a sub-micronewton torsional thrust stand. Measurement. 131, 597-604 (2019).
- Selden, N. P., Ketsdever, A. D. Comparison of force balance calibration techniques for the nano-Newton range. Review of Scientific Instruments. 74 (12), 5249 (2003).
- Pancotti, A. P., Gilpin, M., Hilario, M. S. Comparison of electrostatic fins with piezoelectric impact hammer techniques to extend impulse calibration range of a torsional thrust stand. Review of Scientific Instruments. 83 (3), 035109 (2012).
- Zheng, Y., et al. Improving environmental noise suppression for micronewton force sensing based on electrostatic by injecting air damping. Review of Scientific Instruments. 85 (5), 055002 (2014).
- Zheng, Y., et al. Elegant shadow making tiny force visible for water-walking arthropods and updated Archimedes' principle. Langmuir. 32 (41), 10522-10528 (2016).
- Zheng, Y., et al. The multi-position calibration of the stiffness for atomic-force microscope cantilevers based on vibration. Measurement Science and Technology. 26 (5), (2015).
- Song, L., et al. Highly sensitive, precise, and traceable measurement of force. Instrumentation Science & Technology. 44 (4), 386-400 (2016).
- Zheng, Y., Zhao, M., Sun, P., Song, L. Optimization of electrostatic force system based on Newton interpolation method. Journal of Sensors. 2018, 1-7 (2018).
- Zheng, Y., et al. A multiposition method of viscous measurement for small-volume samples with high viscous. IEEE Transactions on Instrumentation and Measurement. 69 (7), 4995-5001 (2020).
转载和许可
请求许可使用此 JoVE 文章的文本或图形
请求许可探索更多文章
This article has been published
Video Coming Soon
版权所属 © 2025 MyJoVE 公司版权所有,本公司不涉及任何医疗业务和医疗服务。