Method Article
La calibrazione tracciabile del supporto di spinta mediante forza elettrostatica
In questo articolo
Riepilogo
La calibrazione delle caratteristiche meccaniche del cavalletto di spinta è un prerequisito essenziale per garantire la misurazione della spinta in riferibilità. Qui descriviamo come calibrare il supporto di spinta in base alla forza elettrostatica generata dal condensatore a piastre parallele.
Abstract
I micro propulsori hanno importanti applicazioni nel rilevamento di onde gravitazionali a bassa frequenza, nella formazione di satelliti e nella comunicazione laser inter-satellite, quindi è necessario misurare con precisione la spinta dei micro propulsori con tracciabilità. Un supporto di spinta è un dispositivo di misurazione della microspinta ampiamente utilizzato con i vantaggi di un'alta risoluzione e di un carico elevato. La calibrazione delle caratteristiche meccaniche del cavalletto di spinta è un prerequisito essenziale per garantire la misurazione della spinta in riferibilità. In questo studio, un condensatore a piastre parallele è stato utilizzato per calibrare il supporto di spinta generando una forza elettrostatica di micronewton, che potrebbe essere ricondotta al Sistema Internazionale di Unità (SI). L'intervallo di gradiente di capacità costante è stato ottenuto attraverso la simulazione e il calcolo teorico. Inoltre, la forza elettrostatica potrebbe essere modificata dalla tensione standard con i vantaggi del principio semplice, dell'innesco istantaneo e della tracciabilità. Il dispositivo può essere utilizzato per la calibrazione della tracciabilità del supporto di spinta micro newton grazie al semplice assemblaggio e al breve percorso di tracciabilità.
Introduzione
Il micro propulsore è indispensabile per la piattaforma sperimentale spaziale ultra-statica e ultra-stabile per fornire una micro spinta per compensare la forza non conservativa sul veicolo spaziale in tempo reale nel rilevamento di onde gravitazionali a bassa frequenza. La misurazione affidabile della spinta del micropropulsore in un ambiente di rumore complesso è la premessa per ottenere un controllo senza trascinamento. Pertanto, è essenziale calibrare il cavalletto di spinta con elevata precisione per stabilire il modello di risposta meccanica. I metodi di calibrazione del supporto di spinta includono principalmente due tipi, metodi di calibrazione a contatto e senza contatto.
I metodi di calibrazione a contatto includono principalmente il sistema di zavorra a fune, il martello a percussione e il pendolo a percussione, che sono metodi di calibrazione tradizionali. Nel 2002, Lake et al.1 hanno utilizzato pesi e pulegge per applicare la forza di calibrazione nell'intervallo di mN. Nel 2006, Polzin et al.2 hanno anche utilizzato un sistema automatico simile per caricare carichi verticali nel braccio oscillante, ma aveva un grosso errore quando la forza era inferiore a 10 mN. Nel 2004, Koizumi et al.3 hanno ottenuto la quantità di moto generata integrando la forza registrata dal sensore di forza nel processo di collisione. La risoluzione del sensore di forza era di 90 mN, l'impulso effettivo era di 20-80 μN e l'errore totale era di 2,6 μNs a 100 μNs. Il pendolo d'impatto è adatto solo per la misurazione di impulsi di grandi dimensioni, poiché le vibrazioni meccaniche influiscono seriamente sulla calibrazione. Sebbene il metodo di calibrazione del contatto sia facile da configurare, non vi è alcun errore di deriva e la forza calibrata è generalmente maggiore rispetto ai metodi senza contatto. Pertanto, non è adatto per calibrare il supporto di spinta micro forza.
I metodi di calibrazione senza contatto includono principalmente la calibrazione dinamica dei gas, la calibrazione elettromagnetica e la calibrazione elettrostatica. Nel 2002, Jamison et al.4 hanno sviluppato una tecnologia di calibrazione dinamica dei gas, che ha generato un intervallo di forza di 80 nN-1 μN, 86,2 nN di spinta con un errore del 10,7% e 712 nN di spinta con un errore del 2%. La tecnologia di calibrazione dinamica dei gas è in grado di generare una forza di nN e inferiore al μN in modo affidabile ed è facile da implementare. Tuttavia, si tratta di una sorta di tecnologia di calibrazione indiretta che non può risalire al Sistema Internazionale di Unità di Misura (SI). Inoltre, la calibrazione dinamica dei gas è adatta solo nel vuoto.
La forza elettromagnetica può essere piccola quanto l'ordine del micronewton e c'è una buona relazione lineare tra la forza elettromagnetica e la corrente, che ha una buona ripetibilità. Tang et al.5 hanno sviluppato una tecnologia di calibrazione elettromagnetica utilizzando un magnete permanente e una bobina. L'intervallo di misurazione era 10-1000 μNs, la forza di calibrazione era inferiore a 10 mN e l'affidabilità di calibrazione di 310 μN è del 95%. Nel 2013, He et al.6 hanno utilizzato l'elettromagnete ad anello con traferro e il filo di rame eccitato per la calibrazione. L'incertezza di calibrazione di una forza di 150 μN era di 4,17 μN e la forza di calibrazione aveva un ampio intervallo e non era sensibile allo spostamento del braccio di spinta, ma c'era un problema che la corrente del filo di rame avrebbe magnetizzato il nucleo dell'elettromagnete. Nel 2019, Lam et al.7 hanno utilizzato diversi magneti e bobine mobili commerciali per calibrare un'ampia gamma di forze. La struttura era compatta e facile da installare. Inoltre, l'intervallo di forza era ampio, con quattro ordini di grandezza di 30-23000 μN, e le incertezze della forza statica e della forza dell'impulso erano rispettivamente del 18,47% e dell'11,38%. Tuttavia, per la calibrazione del sistema di spinta, la forza elettromagnetica non è riconducibile al SI.
La calibrazione della forza elettrostatica è la tecnica di calibrazione diretta più utilizzata. Selden e Ketsdever8 hanno utilizzato un pettine elettrostatico (ESC) come dispositivo di calibrazione con un campo di misura di decine di micronewton con un errore del 3%. La forza è cambiata del 2% al variare della distanza tra le piastre di 1 mm. Tuttavia, la distanza tra i denti adiacenti dovrebbe essere la stessa, che era applicabile solo al cavalletto di spinta con piccolo spostamento. Nel 2012, Pancotti et al.9 hanno progettato un pettine elettrostatico simmetrico il cui intervallo di impulsi era 0,01 mNs-20 mNs, che potrebbe generare un impulso elettrostatico più grande. Tuttavia, gli svantaggi della struttura complessa e del facile danneggiamento del pettine elettrostatico devono essere risolti.
È un prerequisito fornire la forza tracciabile dei micronewton come forza di riferimento per calibrare il supporto di spinta. La forza elettrostatica è ampiamente utilizzata per tracciare la forza al SI nell'Istituto di metrologia 10,11,12. La forza elettrostatica presenta i vantaggi di un principio semplice, di un innesco istantaneo e di un breve percorso di tracciamento. In questo studio, il condensatore a piastre parallele è stato utilizzato per generare forza elettrostatica come forza di riferimento per calibrare il supporto di spinta del pendolo, la cui uscita di spostamento è proporzionale alla spinta applicata. Il rapporto tra la spinta e lo spostamento è la rigidità del cavalletto di spinta. Calibrando il gradiente di capacità del condensatore, non era necessario controllare rigorosamente la posa di due piastre parallele. L'intervallo di gradiente di capacità costante è stato ottenuto attraverso la simulazione e il calcolo teorico. La gamma di forza elettrostatica poteva essere regolata dalla spaziatura e dall'area di due piastre, che era adatta per una calibrazione efficiente del supporto di spinta con diversa rigidità.
Protocollo
1. Realizzazione sperimentale
- Raccogli tutti i componenti del sistema, incluso il condensatore a piastre parallele circolari, lo stadio lineare motorizzato, il supporto di spinta, il ponte capacitivo, lo strumento SMU, l'interferometro laser e altri componenti, mostrati nella Figura 1.
- Fissare la piastra A sul tavolino lineare motorizzato e fissare la piastra B sul braccio del cavalletto di spinta, rendendo le piastre A e B parallele tra loro.
NOTA: Le piastre vengono lavorate mediante rettifica ad alta precisione della lega di alluminio. Il diametro della piastra A è di 6 cm e il diametro della piastra B è di 4 cm, quindi l'errore di allineamento può essere ignorato. - Controllo della distanza Dab tra le due piastre tramite un tavolino lineare motorizzato (risoluzione 0,625 μm). Montare completamente le due piastre e quindi tirare una distanza fissa di 1 mm attraverso il tavolino lineare.
- Collegare il ponte capacitivo (risoluzione 0,8 aF, precisione ±5 PPM) con le due piastre per misurare la variazione della capacità Cab con la variazione della spaziatura delle piastre.
- Applicare una tensione standard al condensatore con uno strumento SMU (High Voltage Source Measure Unit) (precisione 0,012%, ±5 - ±1100 V) per generare una forza elettrostatica controllabile ad alta precisione.
- Regola l'interferometro laser (risoluzione 10 nm) in modo che sia rivolto direttamente verso il braccio del supporto di spinta e misura lo spostamento x in tempo reale.
2. Calibrazione del gradiente di capacità
- La piastra di azionamento A si sposta lateralmente alla piastra B con una lunghezza del passo di 0,02 mm dal tavolino lineare motorizzato e rende la distanza iniziale della piastra pari a 1 mm.
- Misurare il valore della capacità delle due piastre parallele mediante il ponte capacitivo dopo ogni passaggio fino a quando la variazione relativa della spaziatura delle piastre è di 0,12 mm.
- Iniziare un passo inverso con una lunghezza di 0,02 mm per tornare alla posizione iniziale.
- Conduci un totale di cinque esperimenti ripetibili.
- Adattare i risultati per ottenere la relazione tra il gradiente di capacità e la spaziatura delle piastre del condensatore a piastre parallele, dCab/dDab.
3. Calibrazione della forza elettrostatica del supporto di spinta
- Scollegare il ponte del condensatore dal condensatore a piastre parallele.
- Collegare le due piastre con lo strumento SMU e rendere lo spazio tra le due piastre pari a 1 mm.
- Aumentare gradualmente la tensione U da zero su entrambe le piastre del condensatore con un valore di passo di 50 V fino a quando la tensione applicata è di 300 V. La forza elettrostatica F è pari a 1/2U2(dCab/dDab).
- Usa l'interferometro laser per misurare lo spostamento x del braccio di spinta in tempo reale. Impostare la frequenza di campionamento dell'interferometro laser su 50 Hz.
- Diminuire gradualmente la tensione U da 300 V su entrambe le piastre del condensatore con un valore di passo di 50 V fino a quando la tensione applicata è zero.
- Conduci un totale di cinque esperimenti ripetibili.
- Adattare i risultati per ottenere la relazione tra la forza elettrostatica F e lo spostamento x del braccio del cavalletto di spinta. Calcola la rigidezza k del cavalletto di spinta secondo la legge di Hooke, k = F/x.
Risultati
Seguendo il protocollo, vengono calibrati il gradiente di capacità e la rigidità del cavalletto di spinta. Dovrebbe essere introdotto il principio della forza elettrostatica. Ci sarà un moto relativo Dab tra due piastre cariche sotto l'azione della forza esterna F. Inoltre, l'opera W da una forza esterna sarà convertita in energia elettrica E immagazzinata nel condensatore. Si possono ottenere la differenza di potenziale U, la carica di entrambe le piastre Q e la capacità C . L'energia immagazzinata tra due piastre può essere calcolata secondo l'Eq.(1). Il lavoro svolto dalla forza esterna può essere calcolato secondo l'Eq.(2).
 (1)
(1)
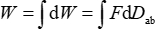 (2)
(2)
Sulla base del principio del lavoro virtuale 13,14,15, W è uguale a E.
 (3)
(3)
La forza esterna cambia la distanza dz tra due piastre, quindi
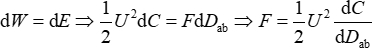 (4)
(4)
Pertanto, la forza elettrostatica può essere calcolata in base alla tensione, purché il gradiente di capacità sia calibrato in base all'Eq.(4). Due piastre metalliche circolari vengono utilizzate per formare un condensatore a piastre parallele.
La Figura 2 mostra la curva di adattamento dei valori medi di capacità e spostamento della piastra A e della piastra B. La media del gradiente di capacità dCab/dDab è di 6,2 pF/mm e la bontà dell'adattamento può raggiungere 0,9983. Pertanto, secondo l'Eq. (4), il condensatore a piastre parallele può produrre una forza tracciabile inferiore a 1 μN (purché la tensione sia inferiore a 17,96 V) e l'intervallo di valori della forza è ~0,279 mN.
La Figura 3A mostra la variazione di spostamento del braccio del cavalletto di spinta al variare della forza elettrostatica. Man mano che la tensione applicata cambia in modo equidistante, ogni spostamento di passo diventa sempre più grande. Si può vedere che lo spostamento cambia simmetricamente all'aumentare della tensione e al diminuire della tensione. La Figura 3B mostra la curva di adattamento dei valori medi dello spostamento del cavalletto di spinta e della forza elettrostatica. La rigidità k del cavalletto di spinta è 3,176 N/m in base all'Eq. (5) e la ripetibilità è 0,0023 N/m.
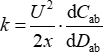 (5)
(5)
La capacità del condensatore a piastre parallele può essere descritta come Eq.(6) a condizione di ignorare l'effetto bordo.
 (6)
(6)
 (7)
(7)
S è l'area di sovrapposizione, la permittività del vuoto ε0 = 8,85 x 10-12 F/m e la costante dielettrica relativa εr = 1 nell'aria. Si può notare che il gradiente di capacità cambia con la spaziatura delle piastre. Tuttavia, la variazione è molto piccola quando la spaziatura delle piastre cambia molto poco. Il gradiente di capacità tende ad un valore costante. Secondo la richiesta della forza standard di magnitudo mN per la calibrazione del supporto di spinta, il diametro della piastra del condensatore a piastre parallele circolari dovrebbe essere compreso nella grandezza centimetrica e la distanza Dab dovrebbe essere compresa nella grandezza millimetrica basata sull'Eq. (1) e (2) quando la tensione di uscita dell'SMU è di poche centinaia di volt. L'intervallo di uscita dello strumento SMU è ±5 μV- ±1100 V. Pertanto, i diametri delle piastre A e B sono rispettivamente di 6 cm e 4 cm. La distanza Dab tra le due piastre è di 1 mm.
Al fine di ottenere l'intervallo di gradiente di capacità costante, la distribuzione del potenziale, la distribuzione del campo elettrico, la capacità e altri parametri del condensatore a piastre parallele con alta tensione vengono calcolati utilizzando la simulazione agli elementi finiti. La distribuzione del potenziale dei condensatori a piastre parallele è mostrata nella Figura 4, le cui dimensioni sono coerenti con il dispositivo reale. Per soddisfare la richiesta di forza elettrostatica di micronewton, la spaziatura tra le piastre è impostata su 1 mm. La Figura 5 mostra la distribuzione del campo elettrico del condensatore a piastre parallele. La freccia rappresenta la direzione del campo elettrico, partendo dall'alta tensione e puntando verso il terminale di messa a terra. La capacità del condensatore a piastre parallele viene simulata modificando la spaziatura delle piastre. La dimensione del passo è di 20 μm e termina a 1,2 mm. Come mostrato nella Figura 6, il gradiente di capacità è un valore costante di 9,81 pF/mm, quando la spaziatura tra le piastre è compresa tra 1 mm e 1,2 mm. Secondo l'Eq.(4), quando il gradiente di capacità è una costante fissa, l'entità della forza elettrostatica ha una relazione lineare con il quadrato della tensione applicata. La Figura 7 mostra la forza elettrostatica simulata a diverse tensioni, che è conforme alla derivazione dell'Eq. (4). Quando la distanza tra due piastre è 1-1,2 mm, per produrre la forza di calibrazione di 1-1000 μN, secondo il calcolo della simulazione, l'intervallo di tensione è 14,29-451,57 V.
Infine, di seguito viene valutata l'incertezza dei risultati della taratura.
1. Valutazione di tipo A dell'incertezza relativa
Le principali fonti di incertezza sono il disturbo dell'aria e le vibrazioni del suolo. Secondo il metodo di Bessel, l'incertezza relativa urel(re) è dello 0,0724% quando il valore medio delle cinque misurazioni viene utilizzato come migliore stima dei risultati della misurazione.
2. Valutazione di tipo B dell'incertezza relativa
un. Incertezza relativa dello spostamento misurata dall'interferometro laser
L'interferometro laser viene utilizzato per misurare lo spostamento del supporto di spinta. L'incertezza relativa dell'interferometro laser senza compensazione è dello 0,005%, che può essere ignorata.
b. Incertezza relativa della tensione applicata dallo strumento SMU
L'incertezza relativa dello strumento SMU è dello 0,012%. Pertanto, l'incertezza relativa introdotta dalla tensione applicata urel(U) è dello 0,012%.
c. Incertezza relativa del gradiente di capacità dCab/dDab
Il gradiente di capacità dCab/ddab si ottiene adattando la capacità misurata dal ponte del condensatore con la distanza percorsa dallo stadio lineare motorizzato. Il ponte capacitivo ha una precisione di 5 PPM, la cui incertezza può essere ignorata. La risoluzione di spostamento dello stadio lineare motorizzato è di 5 μm. Di conseguenza, l'incertezza relativa di dCab/dDab è dello 0,16%.
3. Incertezza estesa
Le componenti di incertezza sono indipendenti l'una dall'altra, riassunte nella Tabella 1. L'incertezza relativa è 0,18%, quindi l'incertezza standard è 0,0057 N/m. L'incertezza relativa introdotta dal gradiente di capacità contribuisce maggiormente. Il fattore di copertura è 3, quindi l'incertezza estesa è 0,0171 N/m.
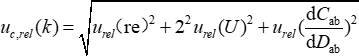 (8)
(8)
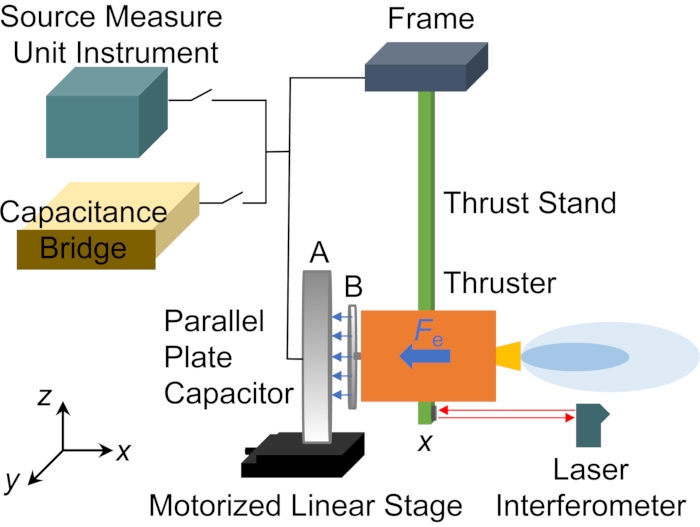
Figura 1: Diagramma schematico del supporto di spinta di calibrazione del condensatore a piastre parallele. Il condensatore a piastre parallele generava la forza elettrostatica come riferimento per la calibrazione del cavalletto di spinta. Clicca qui per visualizzare una versione più grande di questa figura.

Figura 2: Relazione tra la capacità e la spaziatura delle piastre del condensatore a piastre parallele. La pendenza della linea di raccordo era il gradiente di capacità. Clicca qui per visualizzare una versione più grande di questa figura.

Figura 3: Forza elettrostatica che calibra il cavalletto di spinta. (A) Lo spostamento del braccio del cavalletto di spinta. (B) La relazione tra la forza elettrostatica e lo spostamento del braccio di spinta. Clicca qui per visualizzare una versione più grande di questa figura.

Figura 4: Distribuzione del potenziale del condensatore a piastre parallele. La distribuzione del potenziale era uniforme. Clicca qui per visualizzare una versione più grande di questa figura.

Figura 5: Distribuzione del campo elettrico nel condensatore a piastre parallele. Le frecce rappresentano la direzione del campo elettrico. Clicca qui per visualizzare una versione più grande di questa figura.

Figura 6: Simulazione della variazione di capacità con spaziatura delle piastre. La capacità diminuiva con la spaziatura delle piastre. Clicca qui per visualizzare una versione più grande di questa figura.

Figura 7: Simulazione della forza elettrostatica con tensione. La forza elettrostatica aumentava con la tensione applicata al condensatore a piastre. Clicca qui per visualizzare una versione più grande di questa figura.
| Fonte di incertezza | Contributo all'incertezza totale (%) |
| Ripetibilità | 0.07% |
| U | 0.01% |
| dCab/dDab | 0.16% |
| Incertezza relativa combinata | 0.18% |
Tabella 1: Incertezza della taratura del cavalletto di spinta.
Discussione
In questo protocollo, un condensatore a piastre parallele è stato utilizzato per calibrare il supporto di spinta generando una forza elettrostatica di micro-newton, che potrebbe essere ricondotta al SI. È fondamentale per tutte le fasi calibrare con precisione il gradiente di capacità. Lo stadio lineare motorizzato ha reso la distanza iniziale tra le piastre di questo condensatore a piastre parallele pari a 1 mm e ha spostato la piastra A con un passo di 0,02 mm. Il ponte capacitivo è stato utilizzato per misurare la capacità per calibrare accuratamente il gradiente di capacità. La forza elettrostatica può essere calcolata in base alla tensione, purché il gradiente di capacità sia calibrato in base all'Eq.(4).
Il condensatore a piastre parallele per generare la forza elettrostatica in questo protocollo è limitato da un piccolo intervallo. Una tensione troppo alta è difficile da mantenere costante. Pertanto, la forza elettrostatica è adatta solo per calibrare il supporto di microspinta.
Il condensatore a piastre parallele presentava i vantaggi di un principio semplice, di un innesco istantaneo e di una tracciabilità. Il campo di risposta lineare del condensatore a piastre parallele è stato ottenuto attraverso la simulazione e il calcolo teorico, che lo ha reso adatto alla calibrazione della risposta meccanica del supporto di spinta. La forza di riferimento regolata dalla tensione e lo spostamento misurati dall'interferometro laser sono stati ottenuti per completare la calibrazione del supporto di spinta.
La calibrazione tracciabile del supporto di spinta in base alla forza elettrostatica generata dal condensatore a piastre parallele potrebbe essere inferiore a 1 μN in un intervallo di ~0,279 mN, con i vantaggi di un assemblaggio semplice e di un breve percorso tracciabile. La forza misurata dal supporto di spinta è stata ricondotta alla forza elettrostatica tracciabile SI per migliorare l'accuratezza della misurazione. Questo dispositivo ha un'influenza positiva sulla misurazione della microspinta, nonché sulla progettazione e lo sviluppo del propulsore micronewton.
Divulgazioni
Gli autori non hanno nulla da rivelare.
Riconoscimenti
Ringraziamo la National Natural Science Foundation of China (Grant No. 11772202) per aver finanziato questo lavoro.
Materiali
| Name | Company | Catalog Number | Comments |
| Motorized linear stage | Zolix | TSA50-C | Resolution 0.625 μm |
| Capacitance bridge | Andeen-Hagerling | AH2550A | Resolution 0.8 aF, Accuracy ±5 PPM |
| High voltage source measure unit (SMU) instrument | Keithley | 2410 | Precision 0.012%, ±5 μV– ±1100 V |
| Laser interferometer | Renishaw | RLE10 | Resolution 10 nm |
| Circular parallel plate capacitor | Processed by high precision grinding | The plates are processed by high precision grinding of aluminum alloy. The diameter of plate A is 6 cm, and the diameter of plate B is 4 cm. | |
| Thrust stand | Processed by high precision grinding | Pendulum type thrust stand |
Riferimenti
- Lake, J. P., et al. Resonant Operation of a Micro-Newton Thrust Stand[C]. AIAA,38th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit. 3821, (2002).
- Polzin, K. A., Markusic, T. E., Stanojev, B. J., DeHoyos, A., Spaun, B. Thrust stand for electric propulsion performance evaluation. Review of Scientific Instruments. 77 (10), 105108 (2008).
- Koizumi, H., Komurasaki, K., Arakawa, Y. Development of thrust stand for low impulse measurement from microthrusters. Review of Scientific Instruments. 75 (10), 3185 (2004).
- Jamison, A. J., Ketsdever, A. D., Muntz, E. P. Gas dynamic calibration of a nano-Newton thrust stand. Review of Scientific Instruments. 73 (10), 3629 (2002).
- Tang, H., Shi, C., Zhang, X., Zhang, Z., Cheng, J. Pulsed thrust measurements using electromagnetic calibration techniques. Review of Scientific Instruments. 82 (3), 035118 (2011).
- He, Z., et al. Precision electromagnetic calibration technique for micro-Newton thrust stands. Review of Scientific Instruments. 84 (5), 055107 (2013).
- Lam, J. K., Koay, S. C., Lim, C. H., Cheah, K. H. A voice coil based electromagnetic system for calibration of a sub-micronewton torsional thrust stand. Measurement. 131, 597-604 (2019).
- Selden, N. P., Ketsdever, A. D. Comparison of force balance calibration techniques for the nano-Newton range. Review of Scientific Instruments. 74 (12), 5249 (2003).
- Pancotti, A. P., Gilpin, M., Hilario, M. S. Comparison of electrostatic fins with piezoelectric impact hammer techniques to extend impulse calibration range of a torsional thrust stand. Review of Scientific Instruments. 83 (3), 035109 (2012).
- Zheng, Y., et al. Improving environmental noise suppression for micronewton force sensing based on electrostatic by injecting air damping. Review of Scientific Instruments. 85 (5), 055002 (2014).
- Zheng, Y., et al. Elegant shadow making tiny force visible for water-walking arthropods and updated Archimedes' principle. Langmuir. 32 (41), 10522-10528 (2016).
- Zheng, Y., et al. The multi-position calibration of the stiffness for atomic-force microscope cantilevers based on vibration. Measurement Science and Technology. 26 (5), (2015).
- Song, L., et al. Highly sensitive, precise, and traceable measurement of force. Instrumentation Science & Technology. 44 (4), 386-400 (2016).
- Zheng, Y., Zhao, M., Sun, P., Song, L. Optimization of electrostatic force system based on Newton interpolation method. Journal of Sensors. 2018, 1-7 (2018).
- Zheng, Y., et al. A multiposition method of viscous measurement for small-volume samples with high viscous. IEEE Transactions on Instrumentation and Measurement. 69 (7), 4995-5001 (2020).
Ristampe e Autorizzazioni
Richiedi autorizzazione per utilizzare il testo o le figure di questo articolo JoVE
Richiedi AutorizzazioneEsplora altri articoli
This article has been published
Video Coming Soon