Test sensoriale del numero approssimato

Fonte: Laboratorio di Jonathan Flombaum—Johns Hopkins University

Un gioco di carnevale comune è chiedere alle persone di indovinare il numero di gelatine confezionate in un barattolo. Le probabilità che qualcuno ottenga il numero esatto giusto sono basse. Ma che dire delle possibilità che qualcuno indovini 17 o 147.000? Probabilmente anche meno delle possibilità di indovinare la risposta corretta; 17 e 147.000 sembrano semplicemente irrazionali. Perché? Dopotutto, se i fagioli non possono essere tolti e contati uno alla volta, come si può dire che una stima è troppo alta o troppo bassa?

Si scopre che oltre al conteggio verbale (qualcosa di chiaramente appreso), le persone sembrano possedere meccanismi mentali e neurali cablati per stimare i numeri. Per dirla colloquialmente, è ciò che potrebbe essere chiamato una capacità di indovinare, o "ballpark". Gli psicologi sperimentali lo chiamano "Approximate Number Sense" e recenti ricerche con un paradigma sperimentale con lo stesso nome hanno iniziato a scoprire i calcoli sottostanti e i meccanismi neurali che supportano la capacità di indovinare.

In questo video vengono illustrate le procedure standard per l'analisi della stima numerica non verbale con il test approssimativo del senso del numero.

1. Stimoli e prove

1. Programma l'esperimento in Psychopy, MATLAB o qualcosa di simile (una versione gratuita può anche essere scaricata per usi non commerciali a www.panamath.org).
2. Progetta tutte le versioni di prova dell'esperimento in modo che appaiano più o meno uguali.
   1. Dividere il display a metà. Usa uno sfondo grigio.
   2. Un lato del display mostra una raccolta di cerchi blu.
   3. L'altro lato mostra una collezione di cerchi gialli.
3. Disegnare i cerchi in diverse dimensioni, come mostrato nella prova del campione (Figura 1).
   
   Figura 1. Rappresentazione schematica di una singola prova del test approssimativo del senso numerico. In ogni prova, il partecipante riferisce se ha visto più punti blu o gialli.
4. La manipolazione della chiave coinvolge il numero di cerchi gialli e blu. Ci dovrebbe sempre essere più di un tipo rispetto all'altro. La differenza dovrebbe essere caratterizzata in termini di rapporto: 2:1, 1.75:1, 1.5:1, 1.35:1, 1.25:1 e 1.15:1.
5. Istruire il programma a produrre 20 prove con ogni rapporto.
   1. Selezionare casualmente il colore più grande.
   2. Selezionare casualmente il numero minore di cerchi.
   3. Selezionare il numero maggiore per creare il rapporto desiderato.
   4. Disegna cerchi gialli su un lato del display.
   5. Disegna cerchi blu dall'altra parte.
   6. Scegli casualmente il raggio di ciascun cerchio tra 1° (di angolo visivo) e 3,5°.
6. In ogni versione di prova, viene visualizzato un display per 500 ms. Dopo che scompare, il partecipante preme il tasto "Y" se pensa di aver visto più punti gialli, o il tasto "B" se pensa di aver visto più punti blu.
7. Fornisci feedback dopo ogni prova con una schermata che visualizza "Corretto!" o "Errato".

Per rappresentare graficamente i risultati di un partecipante, prestazioni medie in funzione del rapporto su ciascuna prova (Figura 2). Ad esempio, in tutte le 20 prove con un rapporto di 2:1, in quale frazione il partecipante ha fornito la risposta giusta?

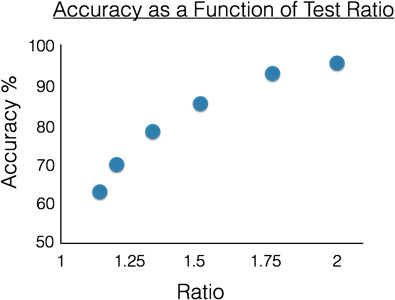
Figura 2. Risultati del campione di un singolo partecipante al test del numero approssimativo. Le prestazioni, misurate come precisione di risposta, aumentano all'aumentare della differenza di rapporto tra il set di punti più grande e quello più piccolo. Poiché il partecipante fa una scelta binaria , gialla o blu più grande - la probabilità è del 50%.

Le prestazioni, misurate come precisione di risposta, aumentano all'aumentare della differenza di rapporto tra il set di punti più grande e quello più piccolo. Poiché il partecipante fa una scelta binaria , gialla o blu più grande - la probabilità è del 50%. Si noti che le prestazioni del partecipante migliorano all'aumentare della differenza di rapporto. Ma la funzione non è lineare, dal momento che c'è un tetto del 100% su quanto bene si può fare. Il fatto che le prestazioni siano vincolate al rapporto suggerisce che l'approssimazione numerica è controllata da un meccanismo analogico o simile alla magnitudine. Un'analogia è utile qui. Immagina di rappresentare due quantità facendo cadere un pugno di sabbia in un secchio per ogni punto visto, un secchio per i punti gialli e uno per i punti blu. È molto improbabile che tu depositi la stessa quantità di sabbia nei secchi su ogni goccia. Quindi diciamo che un secchio rappresenta quattro punti: ha quattro manciate di sabbia al suo. E l'altro rappresenta otto punti: ha otto manciate di sabbia. Potresti pesare i secchi e sapere facilmente quale doveva rappresentare più punti. Ma ora immagina che il secchio più grande fosse pensato solo per rappresentare cinque punti: ha solo cinque manciate di sabbia. Probabilmente peserà ancora più del secchio con quattro, ma non di molto. E poiché a volte potresti prendere un po 'più di sabbia, e a volte un po 'meno, potrebbero anche esserci occasioni in cui il secchio destinato a rappresentare quattro finisce per pesare di più! Questo è un sistema analogico. La rappresentazione, in questo caso la massa di sabbia, fa un buon lavoro nel catturare grandi differenze proporzionali tra le quantità rappresentate, ma a causa del rumore, piccole differenze possono essere difficili da distinguere.

Il risultato è che tali sistemi sono vincolati al rapporto. La capacità di distinguere più o meno dipende dalla differenza di rapporto tra le quantità, non dalla differenza sottrattiva. È facile distinguere otto e quattro come otto e sedici. D'altra parte, otto contro dodici è più difficile, anche se sottrae anche una differenza di quattro.

Le persone differiscono notevolmente tra loro in termini di acutezza del loro senso numerico approssimativo. Per caratterizzare le differenze tra gli individui, gli psicologi sperimentali generalmente testano per trovare il rapporto più piccolo che una persona può distinguere con un'accuratezza del 75%. Come mostrato nella Figura 2, è un rapporto compreso tra 1,25 e 1,5. Questo numero è solo un modo rapido per riassumere quanto sia acuto un senso numerico approssimativo di una persona. Ma al di là del fatto che ci sono grandi differenze tra le persone – una persona potrebbe avere un rapporto di 1: 1 e un'altra potrebbe avere un rapporto di 1: 4, per esempio – queste differenze sono correlate in modo significativo con l'abilità matematica formale. Ad esempio, i rapporti corretti al 75% nei bambini piccoli sono correlati alle abilità aritmetiche misurate da test standardizzati. Questo è sorprendente, perché in definitiva, l'aritmetica non riguarda la stima. Tuttavia, questi tipi di correlazioni suggeriscono che l'abilità matematica formale dipende da un senso numerico approssimativo sottostante.