Charge électrique dans un champ magnétique

Source : Andrew Duffy, Ph.d., département de physique, Université de Boston, Boston, MA

Cette expérience fait double emploi avec la célèbre expérience de J.J. Thomson à la fin du 19^ème siècle, dans lequel il a mesuré le ratio frais de masse de l’électron. En combinaison avec l’expérience de Millikan de la huile-goutte quelques années plus tard qui produit une valeur pour la charge de l’électron, les expériences permis aux scientifiques de trouver, pour la première fois, la masse et la charge de l’électron, qui sont des paramètres clés pour l’électron.

Thomson n’a pas pu mesurer la charge de l’électron ou l’électron de masse séparément, mais il parvint à trouver leur ratio. Le même est vrai pour cette démonstration ; Bien qu’ici il y a l’avantage d’être en mesure de rechercher les valeurs de l’amplitude de la charge de l’électron(e) et la masse de l’électron (m_e), qui sont maintenant tous deux connus avec précision.

Dans cette expérience, un faisceau d’électrons (à l’intérieur d’un tube à vide) et un champ magnétique sont sous le contrôle de l’expérimentateur. Une des idées principales est qu’un champ magnétique peut appliquer une force pour un coût de déménagement. Si l’accusation a une vitesse 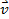et le champ magnétique est 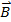, puis l’intensité de la force est donnée par :

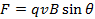(Équation 1)

où q est l’importance de la charge et θ est l’angle entre la vitesse et le champ magnétique. En raison du facteurθ de péché, la force est maximale lorsque la vitesse et le champ magnétique sont perpendiculaires entre eux, et il n’y a aucune force lorsque la vitesse et le domaine sont parallèles entre eux.

Cette force a une direction. La direction de la force est perpendiculaire au plan défini par la vitesse et du champ magnétique (en d’autres termes, la force est perpendiculaire à la fois la vitesse et le champ magnétique). Le sens exact de la force peut être déterminé par la règle de droite. Une version de la règle de droite est le suivant :

À l’aide de la main droite, pointer les doigts dans le sens de la vitesse.

Pensez à la composante du champ magnétique perpendiculaire à la vitesse (la composante parallèle ne produise aucune force). Garder les doigts dans le sens de la vitesse, tournez la main jusqu'à ce que la paume face à la direction de la composante perpendiculaire du champ magnétique.

Coller sur le pouce. Tant que la charge est positive, le pouce doit pointer dans la direction de la force exercée par le champ magnétique sur le coût de déménagement.

Si la charge est négative, alors la force est dans la direction opposée à la façon dont les points de pouce.

Parce que la force est perpendiculaire à la vitesse, la force peut accélérer la particule ni ralentir. Tout ce que la force peut faire est de changer la direction de la vitesse. Dans le cas particulier que la vitesse et du champ magnétique sont perpendiculaires les uns aux autres, le résultat est que la particule chargée suit une trajectoire circulaire, voyageant dans un cercle à vitesse constante. Il s’agit de la définition du mouvement circulaire uniforme, ce qui signifie la seconde loi de Newton peut être appliqué avec l’accélération comme l’accélération centripète.

Dans ce cas :

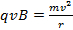(Équation 2)

Cela peut être réorganisé afin de trouver une expression pour le rapport masse sur charge des frais de déplacement :

(Équation 3)

Aux fins de calcul, les deux côtés de l’équation sont élevés au carré :

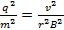(Équation 4)

Re-, qui s’arrange pour :

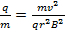(Équation 5)

Cela peut ressembler à une chose étrange à faire, mais notez que dans le numérateur du côté droit, il n’y a moitié de l’énergie cinétique de la particule de charges. Dans l’expérience, les électrons gain énergie cinétique, avant d’entrer dans le champ magnétique, en étant accéléré du reste par une différence de potentiel, V. Appliquant les idées de la conservation de l’énergie :

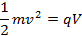
ainsi,

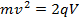(Équation 6)

Insertion de qui dans les résultats de l’équation de masse sur charge dans :

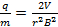(Équation 7)

Donc dans l’expérience, le rapport masse sur charge trouvera en sachant simplement trois éléments d’information, à savoir la tension d’accélération, la force du champ magnétique et le rayon de la trajectoire circulaire suivie par les particules chargées.

La tension d’accélération est serti de V un curseur sur la haute tension d’alimentation, avec un compteur qui peut être utilisé pour lire la tension.

Le champ magnétique B est produit par le courant circulant à travers une paire de bobines, avec une bobine de chaque côté du tube. L’actuel j’ai est lu par un ampèremètre numérique, et les bobines particuliers utilisés créer un champ magnétique de :

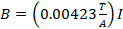(Équation 8)

Vous trouverez le rayon de la trajectoire du faisceau d’une échelle de X-Y bidimensionnelle à l’intérieur du tube (Figure 1). Le courant dans les bobines est ajusté jusqu'à ce que le faisceau d’électrons passe par le point G, qui a les coordonnées (x, Y). Les valeurs X et Y peuvent être facilement lue l’échelle à l’intérieur du tube. Puis, dans le triangle rectangle illustré à la Figure 1, côté OE a une longueur de R-Y, et côté EG a une longueur de X. appliquant le théorème de Pythagore se traduit par

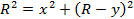(Équation 9)

Résoudre cette équation pour R se traduit par :

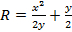(Équation 10)

Il s’agit de toutes les informations nécessaires pour déterminer le ratio masse sur charge.

Figure 1 : schéma de la géométrie pour le faisceau d’électrons. Les électrons, voyageant de gauche à droite, entrez le champ magnétique au point F = (0, 0) et sont ensuite déviés par un champ magnétique dans une trajectoire circulaire qui passe par le point G = (X, Y). Le champ magnétique réglable est créé par deux bobines (connus comme les bobines d’Helmholtz), un de chaque côté du tube. La direction du champ magnétique dans cette image est hors de la page, mais le champ peut être inversé pour que le faisceau se penche vers le haut, au lieu de vers le bas. Le centre de la trajectoire circulaire est au point O. Un triangle rectangle est montré, depuis laquelle on peut déterminer le rayon R .

1. compenser le champ magnétique terrestre

1. Notez qu’il y a deux circuits indépendants dans cette expérience :
   1. Fourniture de courant à des bobines qui créent le champ magnétique ( Figure 2). Le courant est défini par un cadran rotatif, et le circuit comprend un ampèremètre numérique qui permet le courant à mesurer. Un interrupteur va-etvient bipolaire est utilisé pour inverser le sens du courant fourni à des bobines, qui annule le champ magnétique.
   2. Le deuxième circuit ( Figure 3) exécute le tube électronique. Il y a une alimentation haute tension, qui définit la tension d’accélération et un signal alternatif de 6,3 V relié à un filament. Les électrons sont, en quelque sorte, bouilli hors du filament et puis accélérés par la tension d’accélération.
2. Dans le second circuit, allumez l’alimentation haute tension pour allumer le filament. La lumière qui s’allume à l’intérieur du tube est le filament incandescent.
3. Augmentez progressivement le niveau de tension à environ 2 000 V. La partie de l’écran à l’intérieur du tube, qui est touché par le faisceau d’électrons, devrait s’illuminer bleu, visibiliser le faisceau d’électrons.
   1. Note que cela ne signifie pas les électrons sont bleus - le revêtement sur l’écran est phosphorescent et dégage une lueur bleue lorsque les atomes de ce revêtement sont alimentés par les électrons.
4. Ajuster le courant traversant les bobines, qui créent le champ magnétique uniforme. Lorsque le courant est réglé vers le haut ou vers le bas, le chemin du faisceau change. Ajuster le courant pour passer le faisceau à travers un point particulier (X, Y) sur la grille. Prenez note de l’amplitude du courant doit avoir le faisceau passe par ce point.
5. Inverser le courant pour la poutre dans le sens inverse de la courbe et d’ajuster le courant jusqu'à ce que le faisceau passe par le point (X, −Y) (le reflet du point d’origine). Encore une fois, prenez note de l’importance de l’intensité nécessaire pour avoir le faisceau passent par ce point particulier.
6. Vérifier si les amplitudes des deux courants sont différents. À moins que le tube arrive à aligner le faisceau d’électrons est parallèle au champ magnétique terrestre, le champ terrestre s’ajoute au champ des bobines quand le courant est dans une seule direction et soustrait de lui lorsque le courant est dans l’autre sens.
7. Tout au long de l’expérience, moyenne les amplitudes des deux courants, le courant nécessaire pour avoir le faisceau passent par un point particulier (X, Y) sur la grille, et le courant doit pour passer par le point de miroir-image (X, −Y), pour supprimer l’effet du champ magnétique de la terre.

Figure 2 : Schéma de circuit pour les bobines d’Helmholtz. La force du champ magnétique créé par les bobines d’Helmholtz est proportionnelle à la courant passant à travers eux. Le courant fourni à des bobines par le bloc d’alimentation réglable est mesuré par l’ampèremètre numérique. Le but de l’interrupteur double est facilement inverser le sens du courant traversant les bobines, qui provoque une inversion du champ magnétique. Notez que les deux connexions à chaque bobine sont marquées A et Z et les deux Z doit être reliés entre eux pour s’assurer que les bobines produisent des champs magnétiques dans le même sens et pas dans des directions opposées.

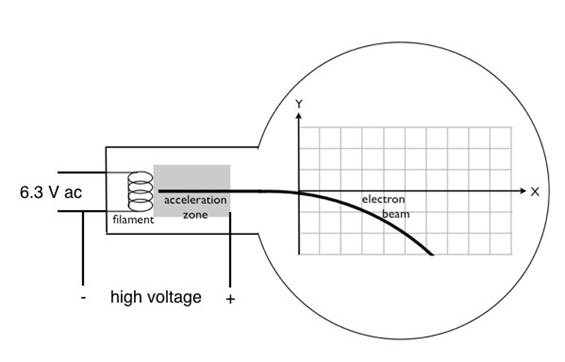
Figure 3 : Schéma électrique pour faire fonctionner le tube éléctron. Le filament incandescent qui est la source des électrons est géré par une source de courant alternatif 6,3 V. Notez que le côté négatif du signal haute tension est également connecté à un côté du filament, tandis que le signal positif de haute tension (l’ordre de 2 000-3 000 V DC) est relié à une électrode sur le côté droit de la zone d’accélération. Ceci produit un champ électrique important réalisé à gauche dans la zone d’accélération, accélérer les électrons de gauche à droite.

2. collecte des données pour un particulier (X, Y) et (X, Y −) combinaison

1. Notez que les tubes sont coûteux et un peu fragile. Ne pas dépasser 3 500 V pour la tension d’accélération et tourner à la tension d’accélération jusqu'à zéro lorsque des mesures ne sont pas prises.
2. Dans cette partie de l’expérience, enregistrer cinq ensembles de données, chacun avec une tension d’accélération différente avec le même (X, Y) et (X, −Y) combinaison.
3. Notez que, comme la tension d’accélération augmente et les électrons voyagent plus vite, ils ne se plient pas autant, et ainsi, le champ magnétique des bobines doit être augmentée pour que le faisceau passe par le même point sur l’écran. Choisir un particulier (X, Y) et (X, −Y) point à utiliser pour cette partie de l’expérience. 10 équation permet de calculer le rayon correspondant de chemin d’accès de la poutre.
4. Pour une tension d’accélération particulier, inscrivez l’amplitude du courant nécessaire pour avoir le faisceau passe par le point choisi (X, Y). Inverser le courant et d’enregistrer l’amplitude du courant nécessaire pour avoir le faisceau passe par le point de miroir-image (X, −Y).
5. Moyenne des deux courants pour supprimer l’influence du champ magnétique terrestre.
6. La moyenne actuelle de l’équation 8 permet de calculer la force du champ magnétique.
7. Les valeurs de la tension croissante, rayon et champ magnétique permet de calculer l’ampleur du ratio masse sur charge de l’électron.
8. Choisissez une nouvelle tension d’accélération et répétez les étapes 2,3 à 2,7. Continuez à faire ceci jusqu'à ce que cinq ensembles de données ont été collectées.
9. Calculer l’ampleur du ratio masse charge moyens pour l’électron.

3. collecte des données pour un particulier de tension d’accélération

1. Recueillir les cinq ensembles de données plus. Cette fois, garder la tension constante accélération et changer le (X, Y) et (X, −Y) points que le faisceau passe à travers. Enregistrer les données.
2. Calculer l’ampleur du ratio masse charge moyens pour l’électron.
3. Les deux rapports masse sur charge déterminées à partir de sources possibles d’état d’erreur dans l’expérience, l’article 2 et 3 en moyenne.

Des résultats représentatifs de l’article 2 peuvent être vu dans le tableau 1. Ces valeurs donnent un ratio moyen de masse sur charge de 1,717 x 10^-11 C/kg. Remarque que c’est l’ampleur du ratio, parce que la charge de l’électron est une valeur négative.

Les résultats représentatifs pour l’article 3 peuvent être vu dans le tableau 1. Ces valeurs donnent un ratio moyen de masse sur charge de 1.677 x 10^-11 C/kg. Encore une fois, c’est l’ampleur du ratio, parce que la charge de l’électron est une valeur négative.

En moyenne sur les deux valeurs de l’amplitude du ratio masse frais et arrondis à trois chiffres significatifs donne une valeur de 1,70 x 10^-11 C/kg.

Ce ratio est connu assez précisément, car la valeur de la charge de l’électron et la masse de l’électron de nombreux chiffres significatifs est connue. À l’aide de ces quantités connues, il peut être déterminé que l’ampleur du ratio masse sur charge est :

1.7588047 ± 0,0000049 C/kg

Notez que la valeur déterminée expérimentalement est environ 4 % de moins que cela. En fait, tous les dix des valeurs sont inférieures à la valeur acceptée, ce qui témoigne d’une erreur systématique. La source la plus probable d’une telle erreur systématique serait dans l’un des compteurs, en particulier le compteur qui indique la valeur de la haute tension. Si ce compteur a donné des lectures qui ont été constamment légèrement inférieures à la valeur réelle, pourrait expliquer les valeurs légèrement faible ratio de masse sur charge par elle-même.

La présence du champ magnétique de la terre n’est pas une source d’erreur, car l’expérience corrigé de l’effet du champ terrestre en faisant la moyenne des deux valeurs actuelles. Toutefois, l’une des hypothèses en dérivant l’équation a été que le champ magnétique produit par des bobines est uniform. Le champ est uniform à l’intérieur d’un solénoïde infiniment long, mais il n’est pas parfaitement homogène dans la région dans les deux serpentins finis utilisés dans cette expérience, qui pourrait être une possible source d’erreur.

X = 7 cm Y = R 1 cm = 25 cm

Tension (V) d’accélération	Grandeur du courant de traverser (X, Y)	Grandeur du courant de traverser (X, −Y)	Courant moyen (A)	Champ magnétique (T)	rapport e/m (C/kg) x 1011
1 800	0.1537	0,1205	0,1371	0.0005799	1,713
2 000	0.1615	0.1242	0.14285	0.0006043	1,753
2 500	0.1800	0.1426	0.1613	0.0006823	1.718
3 000	0.1993	0.1571	0.1782	0.0007538	1,690
3 500	0.2136	0.1694	0.1915	0.0008100	1.707

Tableau 1 : Une table remplie dans la collecte de données pour un particulier (X, Y) et (X, −Y) combinaison.

Tension d’accélération = 2 700 V

X (cm)	Y (cm)	R (cm)	Amplitude du courant de traverser (X, Y)	Amplitude du courant de traverser (X,-Y)	Courant moyen (A)	Champ magnétique (T)	rapport e/m (C/kg) x 1011
7	1	25	0,1875	0.1500	0.16875	0.0007138	1.696
8	2	17	0.2702	0.2270	0.2486	0.001052	1,690
7	2	13,25	0.3378	0.2953	0.31655	0.001339	1.716
9	2	21.25	0.2166	0.1826	0.1996	0.0008443	1.678
10	1	50,5	0.1006	0,0710	0.0858	0.0003629	1.608

Tableau 2 : Une table remplie dans la collecte de données pour une tension d’accélération particulière.

Cette expérience, créée par J.J. Thomson à la fin du 19^ème siècle, a démontré l’existence de l’électron, ce qui en fait une expérience extrêmement importante dans une perspective historique. Électrons ont depuis lors été exploités dans d’innombrables dispositifs électroniques.

Voici une liste de certaines applications de particules chargées qui se rendent dans des chemins circulaires ou en spirale, et donc ils se rendent dans un champ magnétique :

1) la formation des aurores boréales (aurore boréale) et Southern Lights (Aurora Australis) par des particules chargées qui en spirale autour des lignes de champ magnétique de la terre et déposent leur énergie dans les régions polaires.

2) A cathode – ray tube, qui était le fondement de toutes les télévisions, avant les nouvelles technologies d’écrans LCD, LED et plasma.

Spectromètre de masse 3) A. Des spectromètres de masse séparent les ions en fonction de leur masse en pliant leurs trajectoires en chemins circulaires à l’aide d’un champ magnétique. Le rayon de la trajectoire suivie par un ion particulier est proportionnel à sa masse.

4) le Large Hadron Collider (LHC), qui est l’instrument de circonférence célèbre 27 km enterrés le long de la frontière France-Suisse, où les physiciens récemment effectué des expériences pour prouver l’existence du boson de Higgs, qui est responsable de pourquoi les particules ont une masse.