Ondes sonores et décalage Doppler
Vue d'ensemble
Source : Arianna Brown, Antonella Cooray, Ph.d., département de physique & astronomie, école de Sciences physique, University of California, Irvine, CA
Les ondes sont des perturbations qui se propagent dans un espace matériel de moyen ou vide. Ondes lumineuses capable de franchir un vide et certaines formes de la matière et sont transverses dans la nature, ce qui signifie que les oscillations sont perpendiculaires à la direction de propagation. Cependant, les ondes sonores sont des ondes de pression qui voyagent dans un milieu élastique comme l’air et sont longitudinales dans la nature, ce qui signifie que les oscillations soient parallèles à la direction de propagation. Lorsque son est introduit dans un milieu par un objet vibrant, comme les cordes vocales d’une personne ou cordes à piano, les particules dans l’air expérience motion avance et en arrière comme l’objet vibrant se déplace vers l’avant et vers l’arrière. Cela se traduit par régions dans l’air où les particules de l’air sont compressés ensemble, appelé les compressions et autres régions où elles sont écartées, appelé raréfactions. L’énergie créée par une onde sonore oscille entre l’énergie potentielle créée par des compressions et des vitesses des particules du milieu et l’énergie cinétique des petits mouvements.
Compressions et raréfactions peuvent servir à définir la relation entre la fréquence et la vitesse de l’onde sonore. L’objectif de cette expérience est de mesurer la vitesse du son dans l’air et explorer le changement apparent de fréquence pour un objet émettant des ondes sonores en mouvement, appelé l’effet Doppler.
Principles
Comme une onde sonore se propage, il compresse périodiquement et rarefies (étend) les molécules d’air à un endroit. Puisque la relation entre la pression et la densité dépend de la température, la vitesse du son voyage par air est aussi dépendante de la température et définie comme :
 (Équation 1)
(Équation 1)
où TC est la température en degrés Celsius (° C) et v est la vitesse de l’onde sonore, mesuré en mètres par seconde (m/s). Classiquement, la vitesse d’une onde est définie comme :
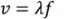 (Équation 2)
(Équation 2)
où λ est la longueur d’onde (m), ou la distance entre les ondes de pression et f est la fréquence (Hz), ou le nombre de vagues par unité de temps. Équation 1 est une estimation pour l’air qui est à l’arrêt ; Si le milieu de l’onde sonore se déplace, la vitesse du son varie selon la direction du mouvement. Par exemple, les ondes sonores se déplaçant en face en direction de vents forts auront probablement sa vitesse a diminué la vitesse du vent. Dans cette expérience, cet effet est négligeable.
Lorsque la source sonore change vitesse ou la direction et le support est que généralement à l’arrêt, il n’y a aucun changement dans la vitesse de l’onde sonore. Toutefois, un observateur peut entendre une fausse augmentation ou diminution de la fréquence à cause de l’effet Doppler. La source des vagues d’accession à l’observateur, les ondes sont émises dans des positions qui sont plus rapprochées. Ils sont toujours émis à la même fréquence, mais en raison de leur position relative que la source se déplace qu’ils atteignent l’observateur en bottes ensemble et apparemment à une fréquence plus élevée. Dans la même logique, lorsque la source s’éloigne de l’observateur, l’observateur entend le son à des fréquences basses. La meilleure façon de comprendre cet effet est d’imaginer une voiture de police avec une sirène conduite vers un piéton : comme il pousse vers le piéton, la fréquence de la zone piétonne semble obtenir plus haut et plus élevés jusqu'à ce qu’enfin la voiture passe le piéton et le piéton commence à entendre des fréquences qui diminuent lorsque les voiture des lecteurs pas. La relation entre la fréquence observée de f et de la fréquence émise f0 est définie par :

où c est la vitesse des ondes sonores dans l’air, v,r est la vitesse du récepteur par rapport à la moyenne et (= 0 si le récepteur est au repos), et vs est la vitesse de la source par rapport à la moyenne.
Dans cette expérience, nous calculer la vitesse du son à l’aide de diverses fréquences et longueurs d’onde et comparer cette vitesse à la vitesse théorique. Nous observerons également l’effet Doppler sur les fréquences émises par un diapason.
Procédure
1. mesure de la vitesse du son
- Mis en place : deux haut-parleurs face à face sur un banc d’optique. Un orateur doit être branché sur un générateur de fonctions (signal) sur un côté d’un té BNC, avec l’autre côté du té BNC connecté au canal A sur l’oscilloscope. Le deuxième orateur doit être branché sur canal B de l’oscilloscope.
- Mettre en marche le générateur de signaux et l’oscilloscope et régler le cadran sur le générateur pour produire une vague de 5 kHz. L’enceinte connectée à l’appareil devrait produire un terrain stable qui sonne comme une alarme et deux vagues devraient apparaître sur l’oscilloscope.
- Introduisez l’enceinte qui est raccordé au canal B le long de l’audience jusqu'à ce que les deux ondes sont en phase. Noter la distance entre les deux enceintes.
- Glisser lentement vers l’arrière l’enceinte du canal B pour que les ondes sont déphasées. Continuer glissant vers l’arrière jusqu'à ce que les ondes sont en phase de nouveau. Enregistrer la nouvelle distance entre les enceintes.
- Soustraire la distance finale de l’initiale de trouver la longueur d’onde du son. Utilisez cette valeur et la fréquence pour calculer la vitesse observée du son à l’aide de l’équation 2.
- Répétez les étapes 1,3 à 1,5 pour les fréquences de 8 kHz et 3 kHz. Notez la relation inversement proportionnelle entre la longueur d’onde et de fréquence.
- Comparer les vitesses expérimentales à la vitesse prévue en utilisant la température de la salle de classe.
2. effet Doppler avec un appareil de diapason/Doppler
La vidéo montre une expérience à l’aide d’un appareil Doppler, mais cette même expérience pourrait être réalisée à l’aide d’un diapason. Le protocole à l’aide d’un diapason est décrit ici :
- Attacher un morceau long de 1 m de chaîne à la fin d’un diapason. Maintenue à la longueur de la taille, le diapason doit se rapprocher de mais pas toucher le sol.
- Connecter un microphone à un canal de l’oscilloscope et placez le micro à une distance fixe (environ 1,5 m).
- Vibrer le diapason pour créer un son et maintenez-le en place à 1,5 m du micro. Notez combien vagues apparaissent sur l’écran.
- Vibrer le diapason à nouveau et commencer à balancer la fourche autour en cercles à une vitesse stabilisée.
- Celles observant que le diapason oscillant remarquerez que comme la fourche oscille vers eux, la fréquence ou pas, obtient plus élevés. En même temps, l’oscilloscope devrait montrer un peu plus de vagues sur l’écran. Comme il balance loin d’eux, le terrain est plus faible et l’oscilloscope devrait montrer un peu moins vagues sur l’écran. Voir Figure 1 ci-dessous pour un exemple d’une vue de l’oscilloscope.
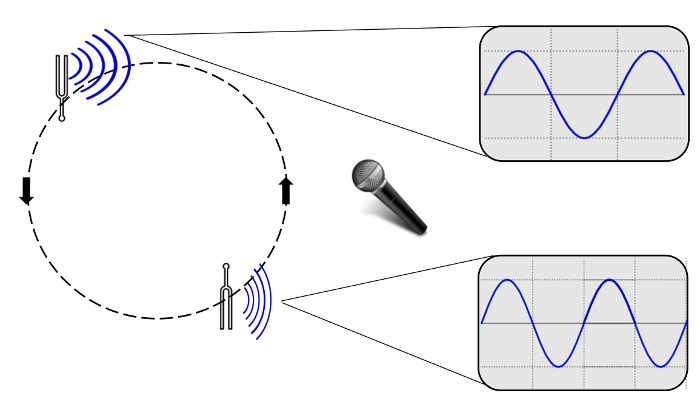
Figure 1 : Représentation des ondes sonores d’un diapason subir l’effet Doppler, telles qu’affichées par un oscilloscope. Comme la fourche oscille vers le micro, les ondes sonores sont émis à des distances plus étroites et créer l’illusion d’un terrain plus élevé. Remarque : Le changement de fréquence des ondes suivi l’écran de l’oscilloscope peut être subtil, et l’amplitude des vagues va aussi changer par rapport à la position de la fourche comme l’amplitude de l’onde sonore est proportionnelle au volume (ou « loudness »).
Résultats
Température ambiante : 20 ° C
Prévu de vitesse : v = 331,4 + 0.6(20) = 343.4 m/s
| Fréquence | Distance en phase initiale | Distance d’en phase finale | Longueur d’onde | Vitesse calculée | % Erreur |
| 5 kHz | 27,4 cm | 34,3 cm | 6,90 cm | 345 m/s | 0,5 % |
| 8 kHz | 25,5 cm | 29,75 cm | 4,25 cm | 340 m/s | 1,0 % |
| 3 kHz | 22,8 cm | 34,2 cm | 11,40 cm | 342 m/s | 0,4 % |
À l’aide de l’équation 2, la vitesse du son peut être calculée sur une valeur assez précise. Par exemple, pour la première fréquence, f = 5 kHz = 5 000 Hz et λ = 6,90 cm = 0,069 m, donc Vitesse = λf = 5 000 x 0,069 = 345 m/s. Pour déterminer l’erreur entre la vitesse attendue et la vitesse observée, nous utilisons ce qui suit :
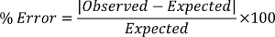
L’effet Doppler se manifesteront par le balancement de la fourche, ou tout autre objet émettant son. Comme le diapason oscille vers le micro, les ondes sonores s’en bottes ensemble produisant une fréquence plus élevée, comme en témoigne le groupage des ondes sonores sur l’oscilloscope. Comme la fourche sera de loin, les vagues deviennent plus étalés et donc de faire des vagues sur l’oscilloscope.
Applications et Résumé
Dans cette expérience, les propriétés de l’onde sonore sont définies et explorées. Plus précisément, la relation entre la fréquence de l’onde sonore, longueur d’onde et la vitesse ont été confirmés. Diapasons sont conçus pour ne émettre qu’une seule fréquence, rendant les dispositifs optimales pour démontrer l’effet Doppler. Que le diapason se rapproche et plus éloigné de l’observateur, la fréquence apparaît supérieur et inférieur aigu, respectivement. L’effet Doppler et l’équation 2 peuvent être étendue à d’autres formes de vagues, tels que la lumière.
En tant qu’humains, nous utilisons des ondes sonores pour communiquer tous les jours. Cependant, une de ces formes de communication représente réellement comment notre espèce exploitée tout d’abord la physique du son : musique, instrument en particulier nécessitant un souffle. Fourche air colonne instruments, comme la trompette, tuba ou flûte, se composent d’une colonne d’air enfermée à l’intérieur d’un tube creux qui est parfois courbé. Comme l’air est poussé dans l’instrument, une vibration se produit à l’intérieur qui provoque des ondes de pression à reflètent sur l’intérieur du tube. Cependant, seulement la pression des vagues de certaines longueurs d’onde et fréquences avec reflètent de telle manière qu’elles commencent à interférer avec l’incident waves ainsi créer ondes de pression permanente. Chaque instrument de musique a un ensemble de fréquences naturelles au cours de laquelle il vibre, ou résonne. Ce qu’on appelle les harmoniques et chaque harmonique est associée à un modèle spécifique des ondes stationnaires défini par ses points de terminaison, longueur d’onde et de fréquence. Dans une flûte, des trous peuvent être ouverts le long de la flûte pour réduire la longueur effective des frontières, donc réduisant la longueur d’onde et augmentation de la fréquence. Dans une trompette, soupapes de rendre l’air traversent les différentes parties de la trompette qui sont de différentes tailles, entraînant des changements dans la longueur d’onde et de fréquence à nouveau.
Une application notable de l’effet Doppler est le radar Doppler, utilisé par les météorologues pour lire les phénomènes météorologiques. En règle générale, un émetteur émet des ondes radio à une fréquence spécifique vers le ciel d’une station météo. Les ondes radio rebondir hors des nuages et des précipitations et puis voyage de retour à la station météo. La fréquence des ondes réfléchie vers la station semblent diminuer si les nuages ou les précipitations vont de la gare, alors que la radio fréquence semble augmenter si les objets atmosphériques sont dirigent vers la station. Cette technologie peut également être appliquée pour déterminer les vitesses de vent et de la direction.
L’effet Doppler a aussi des applications en physique médicale. Dans une échocardiographie Doppler, ondes sonores d’une certaine fréquence sont canalisés vers le cœur et réfléchir hors des cellules sanguines se déplaçant à travers le cœur et les vaisseaux sanguins. Tout comme le radar Doppler, cardiologues peuvent comprendre la vitesse et la direction de la circulation sanguine dans le cœur à cause de la Maj dans les fréquences reçues après réflexion. Cela peut les aider à identifier les zones d’obstruction dans le cœur.
Passer à...
Vidéos de cette collection:

Now Playing
Ondes sonores et décalage Doppler
Physics II
23.5K Vues

Champs électriques
Physics II
77.6K Vues

Potentiel électrique
Physics II
105.2K Vues

Champs magnétiques
Physics II
33.6K Vues

Charge électrique dans un champ magnétique
Physics II
33.7K Vues

Étude sur la loi d'Ohm pour les conducteurs ohmiques et non ohmiques
Physics II
26.3K Vues

Résistances en série et en parallèle
Physics II
33.2K Vues

Capacitance
Physics II
43.8K Vues

Inductance
Physics II
21.6K Vues

Circuits RC/RL/LC
Physics II
143.0K Vues

Semi-conducteurs
Physics II
29.9K Vues

Effet photoélectrique
Physics II
32.8K Vues

Réflexion et réfraction
Physics II
36.2K Vues

Interférence et diffraction
Physics II
91.3K Vues

Ondes stationnaires
Physics II
49.9K Vues