Method Article
La génération de d'ordre supérieur Laguerre-Gauss faisceaux optiques pour l'interférométrie de haute précision
Dans cet article
Résumé
Large laser-interferometers are being constructed to create a new type of astronomy based on gravitational waves. Their sensitivities, as for many other high-precision experiments, are approaching fundamental noise limits such as the atomic vibration of their components. We are pioneering technologies to overcome these limits using novel laser beam shapes.
Résumé
Le bruit thermique dans les miroirs de haute réflectivité est un obstacle majeur pour plusieurs types d'expériences de haute précision interférométrique qui visent à atteindre la limite quantique standard ou pour refroidir les systèmes mécaniques à leur état quantique fondamental. C'est par exemple le cas est prévu des futurs observatoires d'ondes gravitationnelles, dont la sensibilité aux signaux d'ondes gravitationnelles être limitée dans la bande de fréquence la plus sensible, par les vibrations atomiques de leurs masses de miroir. Une approche prometteuse poursuivis pour surmonter cette limitation est d'employer d'ordre supérieur Laguerre-Gauss (LG) faisceaux optiques à la place du mode fondamental classiquement utilisés. En raison de leur distribution d'intensité de lumière plus homogène de ces faisceaux en moyenne plus efficace sur les fluctuations de la surface du miroir, ce qui réduit l'incertitude sur la position du rétroviseur détectée par la lumière laser alimentés en chaleur.
Nous démontrons une méthode prometteuse pour générer desd'ordre supérieur LG faisceaux par mise en forme d'un faisceau gaussien fondamental à l'aide d'éléments optiques diffractifs. Nous montrons que, avec détection conventionnelles et des techniques de contrôle qui sont connus pour stabiliser les faisceaux laser fondamentaux, LG modes d'ordre supérieur peuvent être purifiées et stabilisées tout aussi bien à un niveau comparativement élevé. Un ensemble d'outils de diagnostic nous permet de contrôler et d'adapter les propriétés des faisceaux LG générés. Cela nous a permis de produire un faisceau LG avec la plus grande pureté rapporté à ce jour. La compatibilité démontrée des modes d'ordre supérieur LG avec des techniques d'interférométrie standard et avec l'utilisation d'optiques sphériques standards en fait un candidat idéal pour une utilisation dans une future génération de l'interférométrie de haute précision.
Introduction
Au cours des dernières décennies des expériences de haute précision interférométriques ont été poussés vers un régime de sensibilité ultime où les effets quantiques commencent à jouer un rôle décisif. Dans ces expériences en cours et futurs, tels que le refroidissement laser des oscillateurs mécaniques 1, pièges optiques pour miroirs 2, la production de masses de test intriqués 3, quantique non-démolition interférométrie 4, la stabilisation de la fréquence des lasers à cavités rigides 5, et la détection d'ondes gravitationnelles 6 , 7, 8, les chercheurs sont confrontés à une multitude de limiter les sources de bruit fondamentale et technique. Un des problèmes les plus graves est le bruit thermique des miroirs de la cavité des configurations interférométriques, qui est causée par l'excitation thermique des atomes qui composent les substrats de miroir et le miroir des revêtements réfléchissants 7, 8, 9. Cet effet, appelé aussi le mouvement brownien, va provoquer une incertitude dans la phase dela lumière réfléchie à partir des masses d'épreuve et va donc se manifester par une limitation fondamentale de bruit en sortie de l'interféromètre. Par exemple, la sensibilité de conception projetée avancé ondes gravitationnelles antennes, comme avancée LIGO, Advanced VIRGO, et le télescope Einstein, est limitée par ce type de bruit dans la région la plus sensible de la bande de fréquence d'observation de 10, 11, 12.
Physiciens expérimentateurs de la communauté travaillent dur dans un effort continu pour minimiser ces contributions de bruit et d'améliorer la sensibilité de leurs instruments. Dans le cas particulier de miroir brownien bruit, une méthode pour l'atténuation consiste à utiliser un faisceau plus grande taille de la tache de la norme fondamentale HG 00 faisceau actuellement utilisé sur les surfaces de masse d'essai, puisqu'une plus grande moyenne de faisceau plus efficacement sur les mouvements aléatoires de la surface 13, 14. La densité spectrale de puissance du bruit thermique du miroir a été représentée à l'échelle avecl'inverse de la taille du faisceau gaussien pour le substrat de miroir et avec l'inverse du carré de la surface du miroir 9. Toutefois, comme les taches de faisceau sont faits plus grande, une plus grande fraction de la puissance lumineuse est perdu sur le bord de la surface réfléchissante. Si l'on utilise un faisceau avec une répartition d'intensité radiale plus homogène que le HG 00 faisceau couramment utilisé (voir par exemple la figure 1), le niveau de bruit thermique brownien peut être réduite sans augmentation de ce type de perte. Parmi tous les types de faisceau plus homogènes qui ont été proposées pour les nouvelles versions de l'interférométrie de haute précision, par exemple poutres Mesa ou modes coniques 13, 14, les plus prometteurs sont d'ordre supérieur LG poutres en raison de leur compatibilité potentielle avec le sphérique actuellement utilisé surfaces de miroir 15. Par exemple, le taux de détection des étoiles à neutrons binaire dans les systèmes de spirale - qui sont considérés comme des sources astrophysiques les plus prometteurs pour une première GW détecterion - pourrait être améliorée d'un facteur de 2 ou plus de 16 ans au prix d'un minimum de modifications dans la conception des interféromètres de deuxième génération actuellement en construction 10, 11. En plus des avantages de bruit thermique, les distributions d'intensité plus larges d'ordre supérieur poutres LG (voir par exemple la figure 2) ont été montré pour réduire l'ampleur des aberrations thermiques de l'optique dans les interféromètres. Cela permettrait de réduire la mesure dans laquelle les systèmes de compensation thermique sont invoquées dans de futures expériences d'atteindre des sensibilités de conception 19.
Nous avons étudié et démontré avec succès la faisabilité de générer des faisceaux LG aux niveaux de pureté et la stabilité requises pour opérer avec succès interféromètres GW au meilleur de leur sensibilité 16, 18, 19, 20, 21, 22. La méthode proposée combine les techniques et l'expertise développées dans divers domaines de la physique et de l'optique succèsh comme la génération d'une grande stabilité, un faible bruit laser monomode poutres 23, l'utilisation de modulateurs spatiaux de lumière et des éléments optiques de diffraction pour la manipulation des profils spatiaux des faisceaux lumineux 18, 22, 24, 25, 26, et l'utilisation de des techniques de pointe pour la détection, le contrôle et la stabilisation des cavités optiques résonnantes 27 destinées à une autre purification et la stabilisation de la lumière laser. Cette méthode a fait ses preuves dans les expériences de laboratoire, a exporté pour des tests dans des interféromètres de prototype à grande échelle 20, et pour générer des modes LG aux puissances laser élevées jusqu'à 80 W 21. Dans cet article, nous présentons les détails de la méthode de génération d'ordre supérieur poutres LG et de discuter d'une méthodologie pour la caractérisation et la validation du faisceau résultant. En outre, à l'étape 4 une méthode pour les enquêtes numériques des cavités avec des miroirs non-parfaits 19 est décrite.
Protocole
Préambule: Dans cette section du protocole, nous supposons qu'un pur, à faible bruit, la puissance stabilisée fondamentale mode gaussien faisceau est prévue, par exemple au moyen de la configuration standard comme le montre la figure 3 contenant: un Nd commercial: YAG pour générer en continu lumière infrarouge à onde 1064 nm longueur d'onde, un isolateur de Faraday (FI) pour éviter la rétro-réflexion de la lumière en direction de la source laser et un modulateur électro-optique (EOM) pour moduler la phase de la lumière. Le faisceau ainsi obtenu est injecté dans une cavité optique triangulaire, où la fréquence du laser et la puissance de lumière sont stabilisés au moyen d'un contrôle actif des boucles 27, tandis que la cavité de résonance fournit un filtrage spatial pour les formes de faisceau non désirées.
La configuration décrite ci-dessus et illustré à la figure 3 est un dispositif expérimental classique qui est utilisé dans les appareils scientifiques exigeant la stabilisation du laser de faible bruit de précisionmesures 1-8. La section de protocole ci-dessous décrit comment ce mode faisceau gaussien fondamental peut être efficacement converti en un ordre Laguerre-Gauss type de faisceau optique supérieure avec des performances comparables, sinon identiques, en termes de pureté, le bruit et la stabilité. Ceci est réalisé au moyen de l'appareil représenté dans la figure 4, dont la conception, la construction et le fonctionnement est décrit dans les sections ci-dessous. Dans cet exemple présenté dans cet ouvrage le mode généré sera un LG 33. Toutefois, il convient de souligner que la technique a une validité générale et que le protocole décrit s'applique à tout mode LG d'ordre supérieur désiré.
1. Conception et prototypage le convertisseur de mode optique pour la conversion optimale du mode fondamental faisceau laser en ordre supérieur LG Poutres
L'obligation pour un profil de modulation de phase pour convertir un faisceau de mode fondamental dans un ordre supérieur LG faisceau consiste à reproduire la phase de cross-section du mode LG désiré, qui sera imprimé via un déphasage proportionnel sur le front d'onde du faisceau incident 26. Deux types de mode convertisseurs travail de cette façon: modulateurs spatiaux de lumière (SLM) - écrans à cristaux liquides commandés par ordinateur dont les pixels peuvent être commandés à la phase empreinte déplace sur la lumière incidente - et les plaques de phase diffraction - substrats en verre gravé où le désiraient décalages de phase sont produites dans la transmission par l'épaisseur volontairement variable de l'élément en verre. SLM sont flexibles mais la stabilité et l'efficacité absence, tandis que les plaques de phase sont stables et efficaces, mais le manque de flexibilité. Par conséquent, nous conseillons l'utilisation du SLM pour les études initiales et le prototypage et l'utilisation d'une lame de phase pour des opérations à long terme.
Conversion optimale repose sur le choix précis des paramètres (tour de taille et position) du faisceau d'être façonné. Donc avant de l'injecter sur un convertisseur de mode, le mode fondamental initial soitAM doivent être caractérisés, et ses paramètres remodelé pour correspondre à celles qui offrent conversion optimale - cette opération est appelée «mode d'appariement».
- Ramassez le faisceau de la configuration du mode fondamental décrit à la figure 3.
- Utilisation d'un profileur de faisceau muni d'un logiciel d'analyse d'image en temps réel pour mesurer le rayon du faisceau le long du trajet optique. Une fois un ensemble suffisant de rayons a été acquis (en général au moins 10 points de données sont nécessaires pour un résultat de bonne qualité), monter les rayons mesurée et extraire le tour de taille du faisceau et sa position.
- Mettre en place le rayon requis pour le faisceau au niveau du point de conversion. Utiliser de grandes tailles de faisceau de l'ordre de quelques mm afin de pouvoir utiliser toute l'étendue de la zone de convertisseur de phase.
- Sélectionner un ensemble de lentilles et de leur emplacement le long du chemin optique qui va re-façonner les paramètres du faisceau entrant (tour de taille et de position) dans celles désirées. Aux fins d'alignement, il est commode de placer le convertisseur de mode unT la taille du faisceau entrant.
- Répéter les étapes 1.2 et 1.4 au moyen d'ajustements successifs des positions de la lentille jusqu'à ce que les paramètres de faisceau souhaitées pour la conversion de mode ont été obtenus.
- Positionner le convertisseur de mode SLM le long de la trajectoire du faisceau entrant, et injecter le faisceau sur le SLM. Pour un type SLM réfléchissant, nous vous recommandons d'utiliser un petit angle d'incidence, de l'ordre de 5 degrés ou moins. Grand angle incident ferait l'astigmatisme dans le faisceau généré, brisant le mode symétrie cylindrique LG.
- Appliquer le profil de phase de l'affichage à cristaux liquides SLM - une section transversale de la poutre supérieure pour LG phase souhaitée à être converti en. Le profil de modulation de phase de la 33 en mode LG, qui est actuellement étudiée pour une application dans les futurs détecteurs de GW 16, est illustré dans l'exemple de la figure 5.
- Sélectionner la taille de modèle de phase approprié (de la taille du faisceau correspondant à la configuration de phase) sur la base de la taille de l'injectionTED faisceau. tableau 1 contient une liste de ratios de la taille du faisceau optimales pour les modes LG à l'ordre 9, obtenue à l'aide de simulations numériques 28. En variante, pour le faisceau optimal ratio taille de l'image expérimentalement en faisant varier la taille du motif de phase appliqué au SLM et d'analyser les images de la poutre résultante.
- Observez le faisceau réfléchi par le SLM aide d'une caméra CCD à une distance d'une ou plusieurs plages de Rayleigh loin de la SLM. Alignez soigneusement le SLM afin d'optimiser la symétrie de l'image du faisceau sur le CCD.
Au cours de l'interaction avec le dispositif de modulation de phase, une partie de la lumière injectée reste non modulée grâce à la quantification des niveaux de modulation de phase. Cette lumière non converti se propage le long du même axe du faisceau transformé, altérer les effets de modulation de phase désirées. Pour contourner ce problème, on peut superposer un profil de réseau blazé sur l'image de phase de conversion de mode LG. L moduléight portant le profil de phase du mode LG sera dévié par le réseau blazé, alors que la lumière modulée, qui n'interagit pas avec le substrat, se déroulera tranquillement. Cela provoque une séparation spatiale entre les deux types de poutres.
- Superposer une structure flamboyant au profil de phase précédemment généré sur le SLM. Pour les modes de LG avec azimutale indice l> 0, le motif de phase aura une caractéristique «grille fourchue», comme on le voit dans l'exemple de la figure 6.
- Optimiser l'angle de l'encoche de telle sorte que l'angle de diffraction dans le premier ordre est supérieur à l'angle de divergence du faisceau. Procéder jusqu'à une séparation raisonnable entre des ordres de diffraction plus élevés se trouve (utiliser une séparation entre les bagues extérieures des faisceaux consécutifs aussi grand que le diamètre des anneaux extérieurs eux-mêmes).
- Une fois un motif de conversion optimale est atteinte, passer à la fabrication de la plaque de phase. Ceux-ci sont commercialement dispolable et peuvent être fabriqués pour répondre à un large éventail de besoins personnalisés. Utiliser les résultats obtenus au cours du processus d'optimisation avec le SLM pour définir le motif de conversion de phase optimale pour être gravé sur la plaque de phase. Etape optionnelle: appliquer un revêtement anti-réfléchissant sur au moins l'une des surfaces de la plaque de phase pour minimiser la diffusion de la lumière vers l'arrière de la source laser et de la dispersion de la puissance lumineuse.
2. Le fonctionnement de la Phase Plate, le mode de conversion et de pureté Enhancement
- Remplacez le modulateur spatial de lumière avec la lame de phase. En ce qui concerne la gestion durable des terres, il est commode de le positionner à la taille du faisceau de mode fondamental injecté à convertir.
- Aligner soigneusement la plaque de phase pour le faisceau initial de telle sorte que la lame de phase est perpendiculaire au faisceau et le faisceau est centré par rapport à la structure de phase.
- Propager les faisceaux transmis à travers la lame de phase jusqu'à ce que la séparation ultérieure de la diffdes commandes de raction a lieu. Les poutres peuvent être facilement visualisé avec une carte de faisceau.
- Lorsqu'un suffisamment «bon» séparation est réalisée (comme décrit à l'étape 1.12), obscurcir les rayons de l'ordre de diffraction plus élevés avec une ouverture centrée sur l'ordre de diffraction principal.
L'incapacité des conceptions de la plaque de phase discutés à moduler l'amplitude et la phase signifie qu'ils ne seront pas convertir la totalité du faisceau fondamental entrant dans le mode désiré. Le résultat est une poutre composite avec un faisceau LG dominante souhaitée sur un fond d'autres modes d'ordre supérieur d'intensité mineure, comme le montre la figure 7. Afin de filtrer spatialement les modes LG indésirables et d'améliorer la pureté de mode, le faisceau converti peut être injecté dans une cavité résonante optique. Une telle cavité peut fonctionner comme un «mode de sélection» permettant modes optiques spécifiques uniquement à transmettre, en fonction de la longueur de la cavité par rapport à la longueur d'onde de la lumière.
- Concevoir le mocavité de plus propre. Pour la simplicité de sa mise en oeuvre, l'utilisation d'une configuration de cavité linéaire à deux miroirs, comme le montre la figure 4, dans lequel l'un des miroirs est à plat (en général le miroir d'entrée) et l'autre miroir (sortie) est concave. Cela assure la stabilité optique et la simplicité de mise en œuvre. Une conception spécifique qui donne de bons résultats est celui dans lequel le rayon de courbure du miroir de sortie est de 1 m et la distance entre les surfaces réfléchissantes des miroirs est de 21 cm 29. Dans ce cas, le rayon du faisceau d'entrée optimale est d'environ 365 um à la taille, situés à la surface réfléchissante du miroir plan.
- Choisissez les réflectivités des miroirs de la cavité afin de déterminer la finesse de la cavité. Utiliser un faible finesse de l'ordre quelques centaines à avoir une bonne suppression des ordres en mode non désirées sans introduire de grandes distorsions dues au couplage avec les modes dégénérés (voir l'étape 4). Il est préférable d'utiliser des miroirs avec la même réflectivité de maximiser le débit de la cavité.
- Utiliser un rientretoise gid comme support pour les deux cavité miroirs pour améliorer l'immunité aux vibrations mécaniques. Coller les miroirs sur l'entretoise, et interposer un élément d'anneau piézo-électrique entre l'un des deux miroirs, et l'élément d'espacement pour permettre des ajustements microscopiques de la longueur de la cavité de contrôle de la longueur longitudinale et à des fins de stabilisation.
- Mode correspondre le faisceau engendré par la lame de phase à la cavité de filtre à mode propre-modes. Faisceau profilage d'un faisceau d'atterrisseur ne peut pas être effectué en utilisant les mêmes outils utilisés pour les faisceaux de modes fondamentaux, enregistrer par conséquent, la distribution d'intensité du faisceau avec une caméra CCD placée à des endroits différents le long du trajet de faisceau et analyser les images enregistrées à l'aide de raccord sur mesure scripts qui permettent d'identifier le mode LG souhaité dominante et estimer le rayon du faisceau à la position donnée 30. Un exemple de ce profil intensité procédure de montage du faisceau est illustré à la figure 8.
- Une fois un ensemble suffisant de diamètres de faisceau a êtrefr mesurée (généralement, au moins 10 points de données sont nécessaires pour un résultat de bonne qualité), monter les rayons mesurée et extrapoler le diamètre de la taille du faisceau et son emplacement. Un bon profil de faisceau ressemblera à celui illustré à la figure 9. Comme dans 1.2 et 1.4 certains objectifs et répéter la procédure décrite au point 2.7, 2.8, et 2.9 jusqu'à ce que la taille du faisceau et l'emplacement optimaux sont trouvés. Une fois que le mode d'adaptation est réalisé, injecter le faisceau généré dans la cavité du filtre du mode, en étant sûr que la surface réfléchissante de l'entrée (à plat) miroir est correctement placé à la taille du faisceau injecté.
- Optimiser l'alignement du faisceau injecté dans la cavité, pendant le balayage de la longueur de la cavité en déplaçant le miroir de l'élément piézo, et de surveiller le faisceau transmis.
- L'utilisation des mesures de la lumière transmise par la cavité de filtre en mode en fonction de la longueur de la cavité (également appelé balayages de la cavité) à examiner le contenu de mode du faisceau LG générée par la plaque de phase, et veilleévaluer ntually le rendement de conversion de la plaque de phase elle-même.
- Identifier les modes parasites concernés par l'inspection des images CCD. Évaluer la puissance de ces modes par l'intermédiaire de leur amplitude dans le signal de la photodiode et de calculer la teneur en mode exact du faisceau global. Les résultats de mesure et la teneur en mode exact puissent être reproduites avec et par rapport à des simulations numériques 21. Un bon exemple de cette analyse est donnée à la figure 10, et les résultats en mode de contenu sont présentés dans le Tableau 2.
Une fois l'alignement optimal du faisceau dans la cavité de nettoyage de mode a été atteint, et le contenu de la mode du faisceau injecté a été analysé, «mode de nettoyage" et l'amélioration de la pureté de la LG poutre composite peuvent être finalement mises en œuvre. Un système de verrouillage Pound-Drever-Hall 27 peut être utilisé pour stabiliser la longueur de la cavité pour le mode de résonance souhaitée. La lumière transmise par le mode propre cavité peut être lu par une photodiode, qui peut fournir le signal d'erreur nécessaire pour la boucle de commande qui commande la longueur de la cavité.
- Verrouiller la longueur de la cavité pour les principales images de résonance et d'enregistrement du profil du faisceau résultant transmis par la cavité de la caméra CCD pour diagnostiquer le faisceau produit et qualifier sa pureté.
3. Diagnostics et la caractérisation du faisceau généré par LG
Dans cette expérience, deux propriétés principales définissent la qualité d'un «bon» faisceau pour la mise en œuvre réussie de mesures interférométriques à haute précision: la puissance du faisceau et la pureté du faisceau. D'autres propriétés importantes telles que la fréquence ou la stabilité de puissance peuvent être préservés en utilisant les mêmes techniques de contrôle mis en place sur la poutre en mode fondamental, tel que décrit ci-dessus.
- Mesurer la puissance du faisceau LG au moyen d'un appareil de mesure de puissance laser. Faites attention aux coupures de faisceau: un faisceau LG a une plus grande extensionsion par rapport à un faisceau gaussien classique, et il peut être supérieur à la dimension de la zone sensible pour la plupart des instruments commerciaux. Plus hautes puissances sont évidemment recommandés.
- Évaluer la pureté du faisceau LG généré par comparaison avec un profil de faisceau théorique. Pour ce faire, prendre une photo de l'intensité du faisceau au moyen de la caméra CCD profiler et d'estimer son rayon de faisceau, pour calculer le profil d'amplitude du faisceau théorique à comparer à celle mesurée avec. Évaluer la pureté via le produit scalaire carré
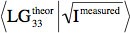 entre la valeur théorique et des distributions d'amplitude mesurées. Puretés élevées sont recommandées.
entre la valeur théorique et des distributions d'amplitude mesurées. Puretés élevées sont recommandées.
Deux figures importantes de mérite sont utiles pour évaluer la qualité de l'ensemble du processus de conversion de mode: les rendements de conversion de la plaque de phase et de la configuration globale.
- Pour évaluer les conversl'efficacité de l'ion de la lame de phase, suivre la procédure cavité de balayage décrit aux étapes 2,11 et 2,12.
- Évaluer l'efficacité de la conversion de la configuration globale comme étant le rapport entre la puissance du faisceau généré souhaitée LG vs la puissance du mode fondamental faisceau gaussien injecté. Des rendements plus élevés sont évidemment souhaitable.
4. L'injection dans les grandes interféromètres: Enquête de simulation
Une application de ce protocole est d'enquêter sur des poutres LG pour leur utilisation dans les détecteurs d'ondes gravitationnelles. Ceux-ci sont longues base interféromètres de haute précision. La ligne de base nécessite relativement grands miroirs et des tailles de faisceau. Toutefois, cela augmente les effets de l'optique imparfaits, en particulier lors de l'utilisation des modes d'ordre supérieur. Cette section décrit une approche basée sur la simulation pour étudier le comportement de la hausse des commandes LG modes de détecteurs réalistes.
- Sélectionnez l'outil de simulation pour modéliser les champs de lumière dans un interferometer afin de tester ordre modes LG élevés. Le logiciel de simulation devrait être capable de modéliser les effets des imperfections dans la configuration (défaut d'alignement, le mode non-concordance, miroir erreur de chiffre, etc) sur le contenu du mode de la poutre. Un exemple est l'outil de simulation FINESSE 28.
- Mettre en place un modèle d'un vrai détecteur à l'aide de l'outil de simulation sélectionné. Dans le cas de cette avancée LIGO est un interféromètre de Michelson à double recyclé avec des cavités de bras de Fabry-Perot. Le but de ces simulations initiales est de vérifier la fiabilité du modèle, en supposant optique parfaits.
- Tester le modèle avec des poutres en mode fondamental parfaits. Pour valider la fiabilité du modèle, ce qui devrait permettre la reproduction d'une liste de procédures expérimentales menées dans le vrai détecteur, tels que: des signaux d'erreur et les contrôles contre les numéros habituels tels que la puissance circulant dans les cavités des bras, des analyses de la cavité, et contrôle angulaire et longitudinal de l'interféromètre et de son sous-systèmes via la télédétection et les systèmes de contrôle. Des simulations doivent inclure la réponse de l'interféromètre à un signal d'onde gravitationnelle. Une fois les simulations fonctionnent comme prévu, le modèle peut être adapté pour commander des modes LG élevés.
- Tester le modèle avec une parfaite LG33 poutres: adapter la conception de l'interféromètre à l'utilisation de modes de LG. Cela nécessite de réduire la taille du faisceau sur les miroirs de la cavité, qui peuvent être obtenus en modifiant les rayons de courbure des miroirs. Une fois que le modèle a été adapté pour le mode LG, les tests effectués en 4.3 doit être répété avec le nouveau faisceau d'entrée. Pour le cas de l'optique parfaites les résultats devraient être très semblables à ceux qui utilisent HG 00 (voir par exemple 19).
L'utilisation de faisceaux d'ordre supérieur présente une «dégénérescence» pour les cavités optiques car il ya plusieurs différentes formes de faisceau luttent pour la domination. Une cavité optique résonnante pour un mode gaussien est résonnante pour tous les modes de cet ordre.Un mode HG00 est le seul mode d'ordre 0, de sorte que tous les autres modes sont supprimées. Par exemple, le mode LG 33 est l'un des dix modes d'ordre 9, qui sera renforcée dans l'interféromètre. distorsions de surface de miroir qui sont toujours présents dans les vrais interféromètres pourrait coupler le mode incident dans d'autres. Si ces nouveaux modes sont du même ordre que le faisceau incident, ils sont renforcés dans les cavités de bras, ce qui entraîne des faisceaux circulant fortement déformées. Cela peut éventuellement détériorer la sensibilité de l'instrument.
- Installation d'un modèle de l'interféromètre réaliste: Incorporer des données réalistes sur les chiffres de la surface des miroirs de la cavité. Ces données prennent la forme d'une «carte» des propriétés de la surface du miroir, telles que la hauteur géométrique ou réflectivité, voir un exemple pour les miroirs LIGO avancée dans la figure 11. Après prise en compte de ces effets, le rendement du mode d'ordre supérieur doit être étudiée, notamment entermes de défauts de contraste à la sortie de détecteur et de la possibilité de plusieurs passages par zéro dans les signaux d'erreur. Dans ces zones, les modes d'ordre supérieur sont tenus d'accomplir pire que HG 00.
- Simulation de sous-systèmes: Afin de mieux comprendre les effets de dégénérescence présents dans le modéliser, de simuler le sous-système dans lequel la dégénérescence provient, par exemple les cavités de bras Fabry-Perot dans LIGO avancée. Simulations de ces sous-systèmes doivent produire des scans de la cavité et des signaux d'erreur pour détecter tout fractionnement de la fréquence et de la détection du champ de circulation qui peut être analysée en termes de contenu de mode.
- exigences Mirror: Derive des exigences plus strictes sur la planéité des surfaces de miroir dans le cas où les résultats de l'étape 4.6 montrent un niveau trop élevé de la fréquence de division ou de la puissance dans les autres modes qui rendraient la mise en œuvre de l'enseignement supérieur pour LG poutres impossible. Pour ce faire, analyser le couplage inter-ordre direct causé par ceune surface qui peut être réalisé numériquement ou en utilisant une approximation analytique 19. Cette méthode permet de déterminer une forme de miroir particulier qui est à l'origine de grandes quantités de couplage entre le faisceau d'entrée et les modes de la même commande. En comparant ces résultats avec les simulations, estimer les besoins en miroir de ces formes, par une pureté spécifique du faisceau circulant. Enfin simuler le modèle de l'interféromètre à grande échelle avec des cartes de miroirs modifiés pour les nouvelles spécifications, illustrant l'amélioration de défaut de contraste et de division de fréquence.
Résultats
All the experimental results so far described in the text and shown in the figures constitute a representative example of a successful execution of the beam conversion protocol. The most representative result is the purity of the generated beam: a successful beam conversion should lead to a beam purity on the order of 95% or above. A good example of successful beam conversion is the measurement of the intensity profile of an 82.8 Watts, 96% pure LG33 beam obtained in 21 and here shown in Figure 12.
Similarly, as discussed in protocol sections, the mode conversion efficiencies of the phase plate and of the overall experimental setup are a good indicator of the successful design of the experimental apparatus, including the phase plate and the mode cleaner cavity. Values of order 50% to 60% and above are generally considered a good value for the mode conversion efficiency. The highest conversion efficiency reported so far with this type of setup is about 70% 21.
The simulation investigation described in Protocol Sec 4 should result in numbers for beam purity with realistic mirrors, suggested mirror specifications and the resulting beam purity when these specifications are adopted. An example of the results you can expect with realistic mirror maps are shown in 19 where an original LG33 purity of 89% is obtained, compared to a purity of >99% for HG00. A purity of >99% for the LG33 mode is achieved using specific mirror requirements with a major reduction of astigmatism in the mirror surface.

Figure 1. Intensity patterns for Hermite-Gauss (HG) modes up to order 6. The intensity patterns are normalized to have the same peak intensity, for visibility.

Figure 2. Intensity patterns for helical LG modes up to order 9. The intensity patterns are normalized to have the same peak intensity, for visibility.
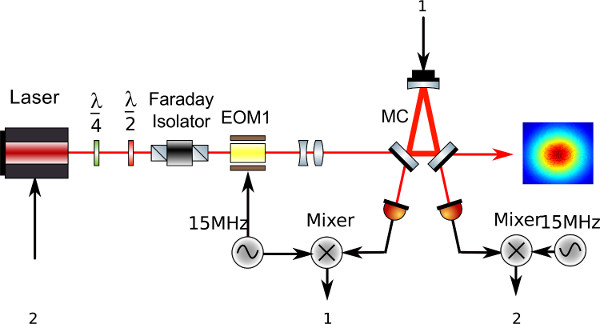
Figure 3. Sketch of a conventional setup for production and stabilization of HG00 beams.

Figure 4. A sketch of the experimental setup discussed in this paper. The HG00 beam is first mode-matched to a desired waist size via a telescope then injected on the phase plate. The main diffracted beam is separated from the higher diffraction orders with an aperture and then sent to the Mode Cleaner cavity. A photodiode is used to extract the error signal for controlling the cavity length. The beam intensity is analyzed by a CCD camera.
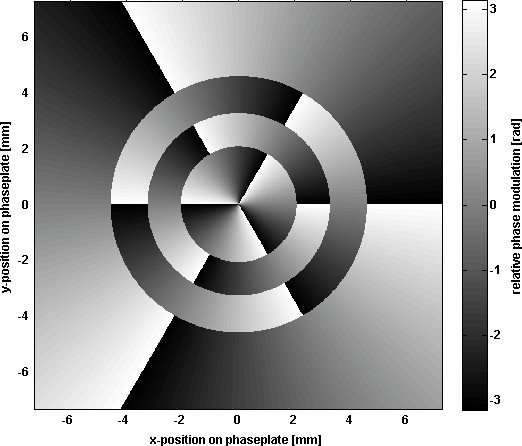
Figure 5. Phase modulation profile to convert a HG00 mode to LG33 mode.
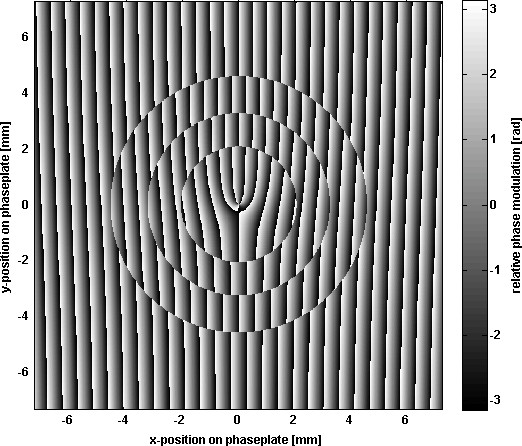
Figure 6. Example of blazed phase modulation profiles for generating LG33 modes.

Figure 7. Comparison between the intensity distribution of the composite beam generated by the phase plate (left) and the theoretical intensity distribution for a pure LG33 beam with same parameters.

Figure 8. Example of beam intensity profile fitting applied to a real LG33 beam transmitted from a phase plate (left) compared to fit results (center) and residuals of fit (right). Click here to view larger figure.

Figure 9. Profile of an LG33 beam with Gaussian fit shown for comparison.

Figure 10. Light power transmitted by a linear cavity as a function of the cavity length, when injecting a beam generated by the phase plate. The resonant peaks at 0 and 1 FSR correspond to the desired LG33 mode. A fit to this dominant mode is shown for comparison (blue line). The red curve shows the result of the numerical model, based on the modal content described in Table 2. Pictures of the unwanted beams to be filtered by the cavity are shown in the insets.
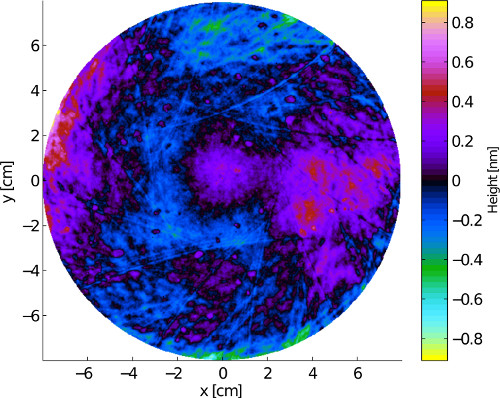
Figure 11. An example of a mirror surface map for one of the Advanced LIGO optical mirrors 19.
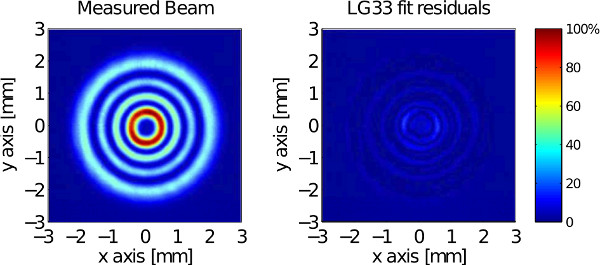
Figure 12. Intensity profile of a 82.8 W LG33 beam transmitted by a linear cavity (left) compared with fit residuals (right).
| p | l | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0 | 1.0 | 2.8 | 1.7 | 2.0 | 2.2 | 2.5 | 2.6 | 3.1 | 3.0 | 3.2 | |
| 1 | 1.7 | 2.7 | 2.2 | 2.4 | 2.6 | 2.8 | 2.9 | 2.8 | |||
| 2 | 2.2 | 2.4 | 2.5 | 2.7 | 2.9 | 3.0 | |||||
| 3 | 2.5 | 2.7 | 2.8 | 3.0 | |||||||
| 4 | 2.9 | 3.0 | |||||||||
Table 1. Optimum ratio between input HG00 beam size and LGpl phase image beam size for LG modes up to the order 9.
| Mode | LG33 | LG63 | LG43 | LG53 | LG32 | LG62 |
| Power | 75% | 8% | 4% | 4% | 4% | 1% |
Table 2. Mode content analysis described by the cavity scan shown in Figure 10.
Discussion
The output beams of most lasers used in high-precision measurements are designed to have a shape well described as a fundamental Gaussian mode. This particular beam geometry combines low diffraction with a spherical wave front. While the low diffraction is one of the key advantages of laser light, the spherical wave front is equally important, as it allows the low-loss transformation of the laser beam by standard optical components with spherical surfaces. Different beam shapes can be created as well, and recently Laguerre-Gauss beams have become of interest for their potential application in high-precision interferometry.
In this paper we demonstrated the experimental procedure to create higher-order Laguerre-Gauss modes with 95% purity for high-power, ultra stable laser beams. To achieve this, we have combined standard techniques from different aspects of optical research, namely diffractive phase plates and laser pre-stabilization to mode cleaner cavities. Our experiment provides a simple, modular and very reliable method to create high power beams in user defined higher-order modes. A commercial ultra-stable laser is used as the light source. Its output is injected to a diffractive phase plate, which can convert up to 75% of the light into the desired Laguerre-Gauss mode. This light is then injected to a small optical cavity and an electronic feedback loop is used to stabilize the laser frequency of the laser to the cavity length. The beam transmitted by the cavity is to 95% in the desired mode and, like the fundamental mode beam at the origin of the setup, has very good frequency stability at audio frequencies. All the parts represent standard components in modern optical experiments. We have successfully demonstrated this technique for laser powers up to 80 W pure Laguerre-Gauss 33 mode.
It could be possible to achieve similar results by replacing the phase plate with another mode-converting element (for example, other diffractive elements or astigmatic mode converters). Alternatively a laser could be setup with an optical resonator tuned for the desired Laguerre-Gauss modes, using for example, an amplitude mask. Finally the laser frequency stabilization to the reference optical cavity could be exchanged with a similar scheme that uses an atomic reference. The need for an electronic feedback system is probably the main disadvantage, but this is inevitable for any light source used for precision interferometer.
However, we believe that the method demonstrated in this paper provides a simple and modular scheme which can be scaled to all ranges of required laser frequency, power, or shape and thus presents a powerful and versatile method. Each part, the laser source, the diffractive element, as well as the optical cavity can be changed or optimized individually, which means that also existing laser injection systems can be upgraded to use Laguerre-Gauss modes.
Déclarations de divulgation
Authors have nothing to disclose.
Remerciements
This work was funded by the Science and Technology Facilities Council (STFC).
matériels
| Name | Company | Catalog Number | Comments |
| The experimental apparatus discussed in this paper requires the following types of instruments: | |||
| Instrument | |||
| Solid state Laser source, Nd:YAG 1064 nm CW laser | Quantity: 1 | ||
| Faraday Isolator | Quantity: 1 | ||
| Electro-Optic Modulator (EOM) | Quantity: 1 | ||
| CCDcamera beam profiler | Quantity: 1 | ||
| Lenses | Quantity: depending on apparatus design | ||
| Steering Mirrors | Quantity: depending on apparatus design | ||
| Aperture | Quantity: 1 | ||
| High reflectivity mirrors (for normal incidence) | Quantity: 2 | ||
| Piezoelectric ring | Quantity: 1 | ||
| Cavity spacer | Quantity: 1 | ||
| Photodiodes and related control electronics | Quantity: 1 or more, depending on apparatus design | ||
| Spatial light modulator | Quantity: 1 Holoeye LCR-2500 | ||
| All the above instruments are commercially available and no particular specification is required. We leave the choice of the most suitable instruments to the experimenter’s discretion. | |||
| For the interest of the experimenter interested in reproducing the protocol, we recommend the following tools used in our experiment: | |||
| Tools | |||
| Innolight OEM 300NE, 1064 nm, 300 mW | Laser Source: | ||
| SIMTOOLs | Software for data analysis, available at www.gwoptics.org/simtools/ | ||
| FINESSE | Software for optical simulations, www.gwoptics.org/finesse/ | ||
| Finally, the phase plate employed in the present experiment was manufactured by Jenoptik GmbH, based on a custom design provided by the Authors. | |||
Références
- Cohadon, P. F., Heidmann, A., Pinard, M. Cooling of a Mirror by Radiation Pressure. Physical Review Letters. 83, 3174-3177 (1999).
- Corbitt, T., et al. An All-Optical Trap for a Gram-Scale Mirror. Physical Review Letters. 98, 150802 (2007).
- Müller-Ebhardt, H., Rehbein, H., Schnabel, R., Danzmann, K., Chen, Y. Entanglement of Macroscopic Test Masses and the Standard Quantum Limit in Laser Interferometry. Physical Review Letters. 100, 013601 (2008).
- Kimble, H. J., Levin, Y., Matsko, A. B., Thorne, K. S., Vyatchanin, S. P. Conversion of conventional gravitational-wave interferometers into quantum nondemolition interferometers by modifying their input and output optics. Physical Review D. 65, 022002 (2001).
- Numata, K., Kemery, A., Camp, J. Thermal-Noise Limit in the Frequency Stabilization of Lasers with Rigid Cavities. Physical Review Letters. 93, 250602 (2004).
- Aufmuth, K., Danzmann, Gravitational wave detectors. New Journal of Physics. 7, 202 (2005).
- Harry, G. M., et al. Thermal noise in interferometric gravitational wave detectors due to dielectric optical coatings. Classical and Quantum Gravity. 19, 897-917 (2002).
- Crooks, D. R. M., et al. Excess mechanical loss associated with dielectric mirror coatings on test masses in interferometric gravitational wave detectors. Classical and Quantum Gravity. 19, 883-896 (2002).
- Yu, L. Internal thermal noise in the LIGO test masses: A direct approach. Physical Review D. 57, 659-663 (1998).
- Harry, G. M. the LIGO Collaboration. Advanced LIGO: the next generation of gravitational wave detectors. Classical and Quantum Gravity. 27, 084006 (2010).
- Accadia, T., Acernese, F., Antonucci, F., Astone, P., Ballardin, G., Barone, F., et al. Status of the VIRGO project. Classical and Quantum Gravity. 28, 114002 (2011).
- Sathyaprakash, B., Abernathy, M., Acernese, F., Ajith, P., Allen, B., Amaro-Seoane, P., et al. Scientific objectives of Einstein Telescope. Classical and Quantum Gravity. 29 (12), 124013 (2012).
- Bondarescu, M., Thorne, K. S. New family of light beams and mirror shapes for future LIGO interferometers. Physical Review D. 74, 082003 (2006).
- Bondarescu, M., Kogan, O., Chen, Y. Optimal light beams and mirror shapes for future LIGO interferometers. Physical Review D. 78, 082002 (2008).
- Tournefier Mours, E., Vinet, J. Y. Thermal noise reduction in interferometric gravitational wave antennas: using high order TEM modes. Classical and Quantum Gravity. 23, 5777 (2006).
- Chelkowski, S., Hild, S., Freise, A. Prospects of higher-order Laguerre-Gauss modes in future gravitational wave detectors. Physical Review D. 79, 122002 (2009).
- Vinet, J. Y. Reducing thermal effects in mirrors of advanced gravitational wave interferometric detectors. Classical and Quantum Gravity. 24, 3897 (2007).
- Fulda, P., Kokeyama, K., Chelkowski, S., Freise, A. Experimental demonstration of higher-order Laguerre-Gauss mode interferometry. Physical Review D. 82, 012002 (2010).
- Bond, C., Fulda, P., Carbone, L., Kokeyama, K., Freise, A. Higher order Laguerre-Gauss mode degeneracy in realistic, high finesse cavities. Physical Review D. 84, 102002 (2011).
- Sorazu, B., et al. Experimental test of higher-order Laguerre-Gauss modes in the 10 m Glasgow prototype interferometer. Class. Quantum Grav. 30, 035004 (2013).
- Carbone, L., Bogan, C., Fulda, P., Freise, A., Willke, W. Generation of High-Purity Higher-Order Laguerre-Gauss Beams at High Laser Power. Physical Review Letters. 110, 251101 (2013).
- Fulda, P., et al. Phaseplate design for Laguerre-Gauss mode conversion. , (2013).
- Willke, B. Stabilized lasers for advanced gravitational wave detectors. Laser & Photonics Rev. , 1-15 (2010).
- Granata, M., Buy, C., Ward, R., Barsuglia, M. Higher-Order Laguerre-Gauss Mode Generation and Interferometry for Gravitational Wave Detectors. Physical Review Letters. 105, 231102 (2010).
- Matsumoto, N., Ando, T., Inoue, T., Ohtake, Y., Fukuchi, N., Hara, T. Generation of high-quality higher-order Laguerre Gaussian beams using liquid-crystal-on-silicon spatial light modulators. J. Opt. Soc. Am. 25, 1642-1651 (2008).
- Kennedy, S. A., Szabo, M. J., Teslow, H., Porterfield, J. Z., Abraham, E. R. I. Creation of Laguerre-Gaussian laser modes using diffractive optics. Physical Review A. 66, 043801 (2002).
- Black, E. D. An introduction to Pound-Drever-Hall laser frequency stabilization. American Journal of Physics. 69, 79-87 (2001).
- Freise, A., Heinzel, G., Lueck, H., Schilling, R., Willke, B., Danzmann, K. Frequency-domain interferometer simulation with higher-order spatial. Class.Quant.Grav. 21, (2004).
- Uehara, N. Mode cleaner for the Initial LIGO 10 Watt Laser. LIGO internal report. 12, (1997).
Réimpressions et Autorisations
Demande d’autorisation pour utiliser le texte ou les figures de cet article JoVE
Demande d’autorisationThis article has been published
Video Coming Soon