用控制容积法测定扁板的撞击力
Overview
资料来源: 里卡多梅希亚-阿尔瓦雷斯和 Hussam Hikmat, 密歇根州立大学机械工程系, 东兰辛, MI
本实验的目的是在物体周围的流动的线性动量的变化的结果显示力量在他们附近使用控制容量公式化 [1, 2]。控制容积分析侧重于对工程系统的宏观影响, 而不是通过差分分析实现的详细描述。这两种技术中的每一个都在工程分析员的工具箱中有一席之地, 它们应该被认为是互补的, 而不是相互竞争的方法。从广义上讲, 控制容积分析将使工程师对系统中的主导负荷有一个概念。这将给她/他一个初步的感觉, 在设计设备或结构时, 应该采取什么途径, 最好是在通过差分公式进行任何详细设计或分析之前, 首先要迈出的第一步。
控制容积公式化的主要原则是用一个被称为控制容积的假想闭合表面所定义的简化的自由体图来取代暴露在流体流动中的系统的细节。该图应包含所有的表面和体力, 通过控制容积的边界的线性动量的净通量, 以及控制容积内的线性动量的变化率。这种方法意味着巧妙地定义控制量, 从而简化分析, 同时捕获对系统的主要影响。这一技术将被证明与平面射流撞击在平板上的不同角度。我们将使用控制体积分析来估计板的空气动力负荷, 并将比较我们的结果与实际测量的产生力获得的气动平衡。
Principles
控制容积 (CV) 由假想的闭合表面定义, 被称为控制面 (CS), 任意定义以研究绕物体和系统的流动效应。图1显示了一个控制卷的示例, 其中包含一个围绕一个实体对象的流区域。在物体的紧邻附近的流动是高度复杂的, 我们希望避免这种复杂性, 以估计流动对支持元素的全球影响。一旦定义, CV 就变成了一个自由体图, 它捕获了流和封闭对象之间的相互作用, 从而在支撑系统中产生负载。为此, 我们将表面和身体的力量等同于 cv 的流动的线性动量的变化。表面力是压力, 流动诱导的剪切, 和任何反应的固体 "切割" 的控制体积。体力基本上是控制容积中所包含的所有物体的重量, 包括固体和液体, 以及由诸如电磁场等体积效应引起的任何其他力。流动的线性动量的变化是动量的净通量的增加的作用通过 CS 和动量的变动率包含在 CV。所有这些作用可以总结在等式为整体形式的线性动量守恒:
 (1)
(1)
这里, 是曲面力, 而是体力. 
 第一个术语在等式的右手边 (1) 代表动量变动率在控制容量之内, 而第二个期限代表净通量动量通过控制表面。向量差异是 CV 和流之间的相对速度, 向量是该区域差异的向外正常的单位.
第一个术语在等式的右手边 (1) 代表动量变动率在控制容量之内, 而第二个期限代表净通量动量通过控制表面。向量差异是 CV 和流之间的相对速度, 向量是该区域差异的向外正常的单位. 
 相对速度和之间的点积表示跨越 CS 的速度分量, 从而有助于线性动量的交换.
相对速度和之间的点积表示跨越 CS 的速度分量, 从而有助于线性动量的交换.  这个点产品的标志是负的, 动量通量是定向到 cv 和积极的地方, 它是远离 cv。在这个形式中, 方程 (1) 是相对于惯性参照系的线性动量的平衡。注意, (1) 是一个向量方程, 这意味着一般是有三独立的组成部分。考虑到这一点, 分析师需要小心地建立一组力量, 平衡每个坐标的线性动量变化。
这个点产品的标志是负的, 动量通量是定向到 cv 和积极的地方, 它是远离 cv。在这个形式中, 方程 (1) 是相对于惯性参照系的线性动量的平衡。注意, (1) 是一个向量方程, 这意味着一般是有三独立的组成部分。考虑到这一点, 分析师需要小心地建立一组力量, 平衡每个坐标的线性动量变化。
对于目前的演示, 我们有图1所示的配置, 其中固定 CV 包含暴露于平面射流的板。由于射流的流动是稳定的, 在 CV 内没有动量的变化, 所以第一个术语在等式 (1) 的右手边消失了。此外, CV 不移动, 因此.  因此, CV 上的力的总和与通过 CS 的动量的净通量相平衡。
因此, CV 上的力的总和与通过 CS 的动量的净通量相平衡。
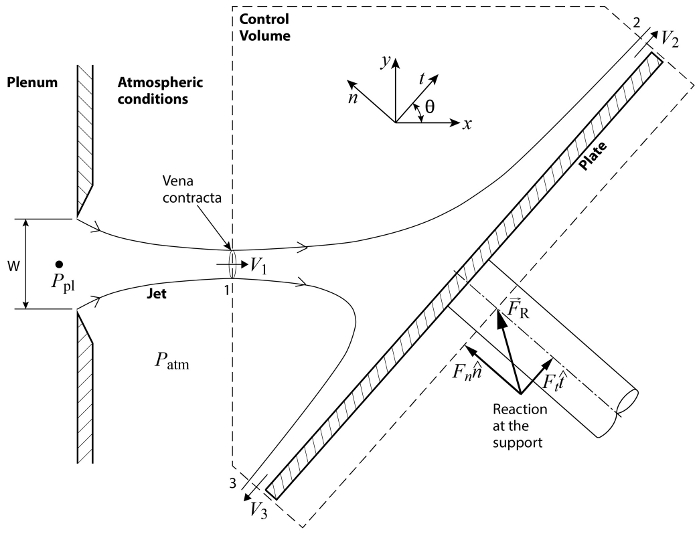
图1.基本配置示意图。一架喷气机通过宽狭缝 W 退出全会 。射流撞击倾斜的板块, 在表面施加载荷时会偏转.
考虑到图1中的配置, 动量通过端口1流入 cv, 并通过端口2和3离开 cv。CV 穿过传入的喷气机在腔 contracta, (有关更多信息, 请参阅视频 "压力和速度的相互作用: 射流撞击斜面板"), 这是流线成为平行的第一个地方, 因此,静止压力横跨喷气机变得同类并且匹配周围的压力的价值, 即大气压.  同样, 端口2和3位于足够远的距离撞击区域, 使流线成为平行和压力, 以适应环境。因此, CS 上的任何地方的压力都等于大气压,.
同样, 端口2和3位于足够远的距离撞击区域, 使流线成为平行和压力, 以适应环境。因此, CS 上的任何地方的压力都等于大气压,.  因此, 由于压力是均匀分布在 CS 周围, 其在控制体积上的净力为零。此外, 由于 cs 是垂直于入口和出口流, 没有任何剪切负荷引起的流量对 cs。总之, 等式 (1) 简化为下面的关系, 如图1所示
因此, 由于压力是均匀分布在 CS 周围, 其在控制体积上的净力为零。此外, 由于 cs 是垂直于入口和出口流, 没有任何剪切负荷引起的流量对 cs。总之, 等式 (1) 简化为下面的关系, 如图1所示
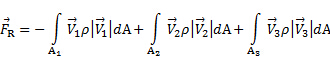 (2)
(2)
这里, 是由射流施加在板上的空气动力载荷的传递所产生的支承系统的反应.  如图1所示, 此反应位于控制音量的一部分, 通过板的支撑系统 "切割"。这被认为是表面力, 在这个意义上, 这个假想的切割将是控制面的一部分。由于是唯一与控制卷无关的与动量通量相关的交互, 所以它是等式 (1) 和 (2) 左侧的唯一术语.
如图1所示, 此反应位于控制音量的一部分, 通过板的支撑系统 "切割"。这被认为是表面力, 在这个意义上, 这个假想的切割将是控制面的一部分。由于是唯一与控制卷无关的与动量通量相关的交互, 所以它是等式 (1) 和 (2) 左侧的唯一术语.  注意从比较这些等式与彼此, 点积在积分的结果简单地在对应的速度向量的大小, 因为他们与区域媒介一致。同样, 如前所述, 他们的星座会告诉你动量通量是否被定向到 CV (-) 或远离它 (+)。如果我们进一步假设, 速度在口岸是近似地均匀的, 并且流动是不可压缩的, 速度和密度可以采取在积分之外, 并且等式 (2) 成为:
注意从比较这些等式与彼此, 点积在积分的结果简单地在对应的速度向量的大小, 因为他们与区域媒介一致。同样, 如前所述, 他们的星座会告诉你动量通量是否被定向到 CV (-) 或远离它 (+)。如果我们进一步假设, 速度在口岸是近似地均匀的, 并且流动是不可压缩的, 速度和密度可以采取在积分之外, 并且等式 (2) 成为:
 (3)
(3)
严格地说, 速度剖面从来都不是完全齐次的, 而这种简化需要一个修正系数的乘法,, 其值取决于速度剖面的详细信息.  在给定的通量端口, 这个系数定义为精确动量通量与从平均速度估计的动量通量的比值:
在给定的通量端口, 这个系数定义为精确动量通量与从平均速度估计的动量通量的比值:
 (4)
(4)
在湍流中, 这个系数是非常接近 1, 因为速度剖面趋于接近均匀。由于这是目前实验的情况下, 方程 (3) 是一个合理的近似的电流测量。但是, 如果流速降低或板块的位置移动到更远的下游, 直到达到层流条件, 有必要解决的右手边的积分 (2) 没有近似。根据图 1, 可以在其正常和切线坐标中分解为板. 
 其中, 和是每个坐标中的单位向量, 和是每个坐标中的投影的大小.
其中, 和是每个坐标中的单位向量, 和是每个坐标中的投影的大小. 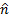

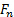
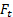
 因此, 方程 (3) 可以分解为:
因此, 方程 (3) 可以分解为:
 (5)
(5)
请注意, 正常组件上的减号会消失, 因为正常轴上的投影为负值.  我们希望通过这项研究来确定平板的正常载荷, 因为它往往是从结构角度来看最相关的部件。从方程 (4), 我们得到的正常载荷板:
我们希望通过这项研究来确定平板的正常载荷, 因为它往往是从结构角度来看最相关的部件。从方程 (4), 我们得到的正常载荷板:
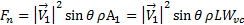 (6)
(6)
这里, 是板块跨度, 是在腔 contracta 的射流宽度. 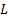
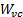 通常, jet 出口宽度、和
通常, jet 出口宽度、和 腔 contracta之间的收缩率非常接近 [2、3、4]:
腔 contracta之间的收缩率非常接近 [2、3、4]:
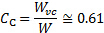 (7)
(7)
总之, 板的正常力可以从以下关系估计:
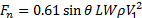 (8)
(8)
在这里, 我们定义以简化操作.  另一方面, 术语的值是使用在充满和
另一方面, 术语的值是使用在充满和 腔 contracta之间的伯努利方程来确定的 (参见图2以供参考)。在内部的速度被认为是微不足道的, 并考虑到喷气机是水平的, 在高度之间的变化和腔 contracta消失。因此, 伯努利方程成为:
腔 contracta之间的伯努利方程来确定的 (参见图2以供参考)。在内部的速度被认为是微不足道的, 并考虑到喷气机是水平的, 在高度之间的变化和腔 contracta消失。因此, 伯努利方程成为:
 (9)
(9)
回想一下, 压力在腔 contracta匹配周围的压力, 这是大气。因此, 在腔 contracta上的动态压力如下:
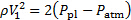 (10)
(10)
方程 (7) 中的方程 (9) 给出了基于平面射流特性的板的正力估计的最终结果:
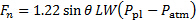 (11)
(11)
这一结果来源于对线性动量守恒的控制量分析。为了评估其准确性, 我们将比较这些估计, 以直接测量的力量。为此, 在图2中描述的水平 (和垂直 (组件) 是由气动平衡捕获的.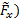
 要确定坐标系上此测量的力的分量, 我们使用以下坐标转换:
要确定坐标系上此测量的力的分量, 我们使用以下坐标转换: 
 (12)
(12)
 (13)
(13)
在其中添加了一个颚化符, 以强调这些力是通过直接测量和气动平衡获得的。
Procedure
1. 设置设施
- 确保设施中没有流动。
- 将压力传感器的正端口连接到压入压力分路器 ().

- 将压力传感器的负端口保持打开到大气 ().

- 将传感器的转换系数从伏特记录到帕斯卡 ().
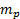
- 记录喷气机出口宽度。
- 记录板块跨度。
- 记录力平衡的转换常数从伏特到牛顿 (水平力:; 垂直力:).


- 设置数据采集系统以100赫兹的速度采样, 共1000年样本 (即10s 的数据)。
- 将撞击板安装在力平衡上, 并将其输出调整为零。
2. 记录数据
- 将板的角度设置为 90o (请参阅图 2以供参考)。
- 打开流设备。
- 将压力传感器的读数记录在伏特中, 对应于大气压和大气之间的压力差 ().
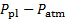
- 使用数据采集系统记录力数据。
- 通过强制转换因子 (和) 将获取的值乘以 (伏特), 并在表1中输入结果.


- 关闭流设备。
- 改变板的角度。
- 为下列角度重复步骤2.2 至 2.6:

图2。实验设置。(A): 进气系统的详细信息在压力下增压全会.  (B): 放电侧有撞击板。(C): 放电狭缝的细节.请单击此处查看此图的较大版本.
(B): 放电侧有撞击板。(C): 放电狭缝的细节.请单击此处查看此图的较大版本.
3. 数据分析
- 用方程 (11) 计算天平的正力, 并将其记录在表1中。
- 从方程 (10) 中确定正力的理论值, 并将其记录在表1中。
- 计算两个值之间的不一致百分比。
表1。实验研究的基本参数。
| 参数 | 值 |
| 喷嘴宽度 (W) | 19.05 毫米 |
| 板跨度 (L) | 110.49 厘米 |
| 传感器校准常数 (m_p) | 141.3829 Pa/五 |
| 平衡水平系数 (m_x) | 22.2411 N/伏 |
| 平衡垂直系数 (m_y) | 4.4482 N/伏 |
Results
图 3显示了将平板上的正常负载与空气动力平衡直接测量和线性动量守恒估计的比较。在一般情况下, 线性动量的分析捕获了直接测量的主要趋势, 即撞击角的变化。这些测量中的差异与撞击角不单调变化。对于范围内的冲击角, 对于, 差异小于 6%. 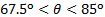
 他们是较高的其他角度, 但从来没有高于12.5%。似乎有一个在的交叉, 其中的差异趋势反转: 测量显示更高的正常负载比分析的线性动量为和较低的.
他们是较高的其他角度, 但从来没有高于12.5%。似乎有一个在的交叉, 其中的差异趋势反转: 测量显示更高的正常负载比分析的线性动量为和较低的. 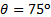

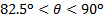 这些倾向的区别可能归结于事实线性动量的分析假设无粘, 非耗散, 线性动量的变动, 而直接测量不可能避免黏度的作用对流动。对于范围, 切变分量将成为主导, 因此湍流边界层效应可能很重要.
这些倾向的区别可能归结于事实线性动量的分析假设无粘, 非耗散, 线性动量的变动, 而直接测量不可能避免黏度的作用对流动。对于范围, 切变分量将成为主导, 因此湍流边界层效应可能很重要.  在这种情况下, 由于湍流引起的壁面正常的速度波动可能导致正常负载的增加。另一方面, 射流的轴向速度在的范围内有明显的减小, 而当它变成主要与壁相切时.
在这种情况下, 由于湍流引起的壁面正常的速度波动可能导致正常负载的增加。另一方面, 射流的轴向速度在的范围内有明显的减小, 而当它变成主要与壁相切时. 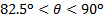 这种效应很可能使粘度消散由于雷诺数的局部值减少, 这将导致减少的正常负荷值。
这种效应很可能使粘度消散由于雷诺数的局部值减少, 这将导致减少的正常负荷值。
Table2.代表结果.
| θ | f#̃_x (N) | f#̃_y (N) | f#̃_n (n) | F_n (n) | ε (%) |
| 90o | 15.257 | 9.034 | 15.257 | 16.773 | 9。9 |
| 85o | 15.151 | 9.831 | 15.950 | 16.709 | 4。8 |
| 82.5o | 15.035 | 10.231 | 16.242 | 16.630 | 2。4 |
| 80o | 15.929 | 10.498 | 17.510 | 16.518 | 5。7 |
| 75o | 14.248 | 10.453 | 16.468 | 16.202 | 1。6 |
| 70o | 13.518 | 11.405 | 16.604 | 15.762 | 5。1 |
| 67.5o | 13.100 | 11.294 | 16.425 | 15.496 | 5。7 |
| 65o | 12.771 | 11.579 | 16.468 | 15.202 | 7。7 |
| 60o | 11.881 | 11.863 | 16.221 | 14.526 | 10。5 |
| 50o | 9.746 | 11.241 | 14.691 | 12.849 | 12。5 |
| 40o | 6.357 | 9.444 | 11.320 | 10.782 | 4。8 |

图3.代表性的结果。由于撞击射流, 在板上装载。符号表示:  : 直接负载测量;
: 直接负载测量; : 来自线性动量守恒的估计;: 实验测量和理论估计之间的百分比误差.
: 来自线性动量守恒的估计;: 实验测量和理论估计之间的百分比误差.  请单击此处查看此图的较大版本.
请单击此处查看此图的较大版本.
Application and Summary
通过对线性动量守恒控制体积分析的应用, 确定了射流撞击平板的受力。这一分析证明简单适用, 并给出了满意的体积估计的负荷不需要详细了解的流动模式周围的板块。虽然由于动量的无粘变换的基本假设存在一些差异 (无论是大小还是趋势), 这项技术提供了一种方法, 可以获得系统行为的快速估计, 而无需深入研究流体流动。因此, 这是一个强大的工具, 工程分析师, 例如, 预测的可行性, 开发一个给定的工程系统的时间和资源的最小投资。一旦进行了第一次分析, 以确定可行性, 工程师可以进入一个更详细的流量分析使用, 例如, 计算流体力学。
线性动量守恒的控制体积分析是流体工程的有力工具。它发现在各种各样的问题上的应用, 以规避更多涉及的方法, 如差异分析。此分析的几个实例可以描述如下:
式涡轮叶片设计: 一般情况下, 式涡轮叶片应设计成将最高的线性动量转化为扭矩。这是通过确定叶片的几何形状, 使水射流的线性动量的变化最大化。为此, 控制卷分析的典型结果是, 应该使 jet 自行翻转, 即 180o。对于旋转设备来说, 这通常是一个技术难题, 但对于使用其他工具进行更详细的分析, 则给分析人员提供了初步的指导。
在民用结构上拖动负载: 土木工程的一个挑战是设计承受风荷载的结构。为了预测风对实际尺寸结构的影响, 可以在风或水隧道中进行低尺度模型的试验。为此, 可以根据模型的上游和下游的速度测量, 利用控制体积分析的线性动量守恒来确定原型的有效载荷。该方法既简化了实验运动, 又节省了时间、精力和资金, 为实际结构的建设做好了准备。
跳至...
此集合中的视频:

Now Playing
用控制容积法测定扁板的撞击力
Mechanical Engineering
26.0K Views

浮力和拖曳在浸没的身体
Mechanical Engineering
30.2K Views

浮动容器的稳定性
Mechanical Engineering
23.3K Views

推进力和推力
Mechanical Engineering
22.1K Views

管道网络和压力损失
Mechanical Engineering
58.8K Views

淬火和沸腾
Mechanical Engineering
8.2K Views

液压跳跃
Mechanical Engineering
41.3K Views

换热器分析
Mechanical Engineering
28.3K Views

制冷概论
Mechanical Engineering
25.0K Views

热丝测速
Mechanical Engineering
15.9K Views

测量紊流
Mechanical Engineering
13.6K Views

通过钝体流的可视化
Mechanical Engineering
12.2K Views

射流撞击斜面板
Mechanical Engineering
10.8K Views

系统分析中的能量守恒方法
Mechanical Engineering
7.4K Views

质量守恒和流速测量
Mechanical Engineering
23.0K Views
版权所属 © 2025 MyJoVE 公司版权所有,本公司不涉及任何医疗业务和医疗服务。