Reflection and Refraction

When light hits the interface between two materials, it is bent by some angle that depends on the composition of the two materials. At the boundary, the speed at which the light propagates changes, causing its direction of propagation to change as well. Each medium has a characteristic “index of refraction” that is defined as the ratio between the speed of light in vacuum and the speed of light in the medium:

where n is the dimensionless index of refraction, c is the speed of light in vacuum in meters per second (m/s), and v is the speed of light in the medium in meters per second (m/s). Light travels more slowly in a medium with a high index of refraction and more quickly in a medium with a low index of refraction.

For a given angle of incidence, ө_i (angle at which the light hits the boundary between the two media), the angle at which the light beam is refracted, ө_r, is given by the Law of Refraction, which is more commonly known as Snell’s Law:

where ө_i and ө_r are in degrees, and n1 and n2 are the dimensionless indices of refraction of the initial and final materials through which the light is traveling. The refraction angle specifies the direction in which the refracted light wave will travel in the second medium (see Figure 1). Some fraction of the incident light is also reflected back into the first medium at an angle equal to the angle of incidence.

An interesting phenomenon occurs when light goes from a material with a high index of refraction to one with a lower index. There is a critical incident angle at which the refracted angle will become 90°. If light hits the boundary at the critical angle, the refracted beam will travel along the boundary between the media, and some light will be reflected back into the high index of refraction material (see Figure 2). If light hits the boundary at an angle greater than this critical angle, it will be completely reflected back into the high index of refraction material in an event called total internal reflection.

Figure 1: An incident light ray on the boundary between two media results in a reflected ray and a refracted ray.

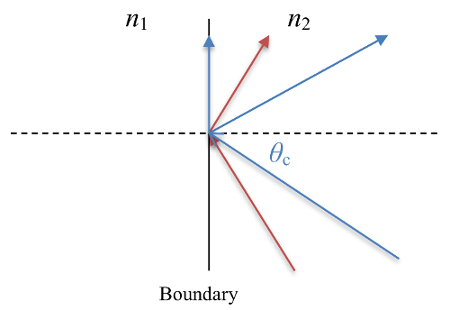
Figure 2: Total internal reflection when n₂ > n₁. The blue ray is incident at the critical angle and results in a refracted ray traveling along the interface and a reflected ray. The red ray is incident at an angle larger than the critical angle and leads to a totally internally reflected ray.

Lenses take advantage of refraction to create real and virtual images of objects. A real image is an image formed by the physical convergence of light rays that came from an object. A virtual image is formed when light rays appear to converge but do not actually physically converge. Our eyes construct a point of origin for diverging rays, and this point of origin serves as the source of the virtual images even though the light rays do not actually converge at this point. Examples of real and virtual images formed by a convex lens are shown in Figure 3. Lenses have a characteristic length called the “focal length”, which is the distance from the lens at which the light rays originating infinitely far away will be focused after passing through the lens. Given the focal length of a lens, the distance between the object and the lens will determine the location of the image according to the thin lens equation:

Where f is the focal length of the lens in meters (m), o is the distance between the lens and object in meters (m), and i is the distance between the lens and image in meters (m). If the object distance is taken to be a positive quantity, then, if the image distance is positive, the image will be real and will be located on the side of the lens opposite to the object. If the image distance is negative, the image will be virtual, magnified, and located on the same side of the lens as the object.

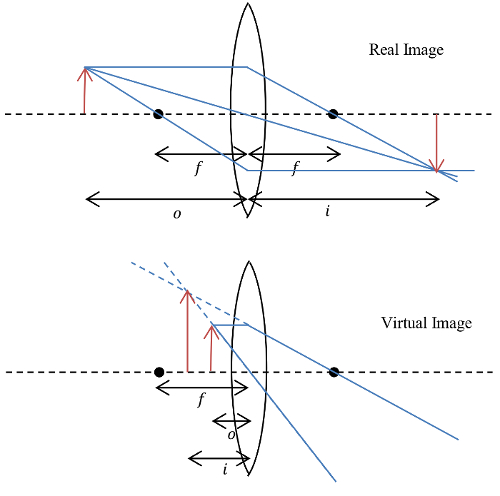
Figure 3: A convex lens producing real and virtual images. Real images form from the true convergence of light rays. Virtual images are constructed by our eyes from diverging light rays.

Snell’s Law dictates the angle at which light will be bent when crossing the boundary between two media. The measured incident and refracted angles at the water-air interface are given in Table 1. Below, a sample calculation giving the index of refraction for water using Snell’s Law is shown for an angle of incidence equal to 30.1° as the light goes from the water to air:

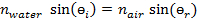
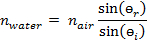
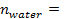1.33

The calculation can be repeated for the various angles in Table 1, and the average of the measurements will provide an even better measurement of the index of refraction than any of the individual measurements will provide.

Table 1: Results.

Interface	өi	өr	nwater
Water → Air	10.0	13.5	1.34
Water → Air	19.8	26.6	1.32
Water → Air	30.1	41.9	1.33
Air → Water	20.1	15.1	1.32
Air → Water	44.9	32.0	1.33
Air → Water	75.2	46.7	1.33

The critical angle for total internal reflection occurs when the refraction angle is equal to 90°. For the water-air interface, Snell’s Law predicts that the critical angle of incidence is 48.8°.

It is worthwhile to note that the refracted beam could still be observed at an angle greater than 48.8° when looking at the interface at which the light beam went from air into the water. It is only at the boundary at which the beam went from the water to the air that the beam was internally reflected at angles greater than 48.8°. Total internal reflection can only occur when light goes from a medium with a high index of refraction to a medium with a lower index of refraction.

For the lens part of the experiment, when the object was placed at about o = 11.02 cm, the image came into focus at about 9.21 cm. The thin lens equation then reveals the focal length of the convex lens to be about 5.02 cm.

This lab explores the physics of refraction and lenses. Snell’s Law was used to measure the index of refraction for water using measurements of incident and refracted angles. The phenomenon of total internal reflection at the water-air interface was also observed. It was shown that concave lenses can focus light and also create virtual images, allowing them to serve as magnification devices.

The human eye sees by focusing light onto the retina, and poor vision can result if the light focuses in front of or behind the retina. Eyeglasses help to correct poor vision by properly refocusing the light onto the retina. Cameras use a lens to focus light onto a sensor the same way that eyes focus light onto the retina. Magnifying glasses are simply convex lenses that create enlarged, virtual images of objects. Optical microscopes use multiple lenses to immensely magnify small objects, such as cells. Similarly, there is a type of telescope called a refractor that uses lenses to capture the light from stars, galaxies, and other astrophysical objects. Total internal reflection is used most often in the form of optical fibers, which are used for data transmission and as fiberscopes.