Reflexão e Refração
Visão Geral
Fonte: Derek Wilson, Asantha Cooray, PhD, Departamento de Física & Astronomia, Escola de Ciências Físicas, Universidade da Califórnia, Irvine, CA
A luz viaja em velocidades diferentes, dependendo do material pelo qual está se propagando. Quando a luz viaja de um material para outro, ele vai desacelerar ou acelerar. Para conservar energia e impulso, a luz deve mudar a direção em que se propaga. Esta dobra de luz é conhecida como refração. Alguma fração da luz também é refletida na interface entre os dois materiais. Em casos especiais, um feixe de luz pode ser refratado tão acentuadamente em uma interface que é realmente completamente refletida de volta para o meio de onde ele estava vindo.
As lentes fazem uso do princípio da refração. As lentes vêm em duas variedades com curvaturas diferentes: lentes convexas e lentes côncavas. As lentes convexas são frequentemente usadas para focar a luz, mas também podem ser usadas para criar imagens ampliadas de objetos. Quando uma lente convexa faz com que os raios de luz provenientes de um objeto divergam, o olho humano julga que a luz vem de algum ponto atrás do objeto real do qual a luz está se originando. A imagem do objeto será ampliada neste caso. Esse tipo de imagem é chamada de imagem virtual. As lentes côncavas também podem fazer com que os raios de luz divergam e criem imagens virtuais, embora a imagem seja desmagnizada.
Este laboratório demonstrará a lei fundamental da refração e examinará as maneiras pelas quais as lentes criam imagens.
Princípios
Quando a luz atinge a interface entre dois materiais, ela é dobrada por algum ângulo que depende da composição dos dois materiais. No limite, a velocidade com que a luz se propaga muda, fazendo com que sua direção de propagação também mude. Cada meio tem um "índice de refração" característico que é definido como a razão entre a velocidade da luz no vácuo e a velocidade da luz no meio:

onde n é o índice a dimensionável de refração, c é a velocidade da luz no vácuo em metros por segundo (m/s), e v é a velocidade da luz no médio em metros por segundo (m/s). A luz viaja mais lentamente em um meio com um alto índice de refração e mais rapidamente em um meio com baixo índice de refração.
Para um determinado ângulo de incidência, өi (ângulo em que a luz atinge o limite entre as duas mídias), o ângulo em que o feixe de luz é refratado, өr,é dado pela Lei de Refração, que é mais conhecida como Lei de Snell:

onde өi e өr estão em graus, e n1 e n2 são os índices a dimensionados de refração dos materiais iniciais e finais pelos quais a luz está viajando. O ângulo de refração especifica a direção em que a onda de luz refratada viajará no segundo meio (ver Figura 1). Alguma fração da luz incidente também é refletida de volta para o primeiro meio em um ângulo igual ao ângulo de incidência.
Um fenômeno interessante ocorre quando a luz vai de um material com alto índice de refração para um com um índice menor. Há um ângulo crítico de incidente no qual o ângulo refratado se tornará 90°. Se a luz atingir o limite no ângulo crítico, o feixe refratado viajará ao longo da fronteira entre a mídia, e alguma luz será refletida de volta no alto índice de material de refração (ver Figura 2). Se a luz atingir o limite em um ângulo maior do que este ângulo crítico, ela será completamente refletida de volta para o alto índice de material de refração em um evento chamado reflexão interna total.

Figura 1: Um raio de luz incidente na fronteira entre dois meios de comunicação resulta em um raio refletido e um raio refratado.
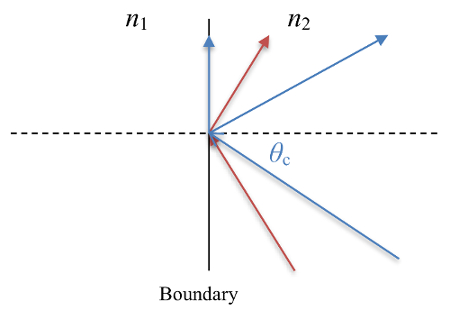
Figura 2: Total de reflexão interna quando n2 > n1. O raio azul é incidente no ângulo crítico e resulta em um raio refratado viajando ao longo da interface e um raio refletido. O raio vermelho é incidente em um ângulo maior que o ângulo crítico e leva a um raio totalmente refletido internamente.
As lentes aproveitam a refração para criar imagens reais e virtuais de objetos. Uma imagem real é uma imagem formada pela convergência física de raios de luz que vieram de um objeto. Uma imagem virtual é formada quando os raios de luz parecem convergir, mas não convergem fisicamente. Nossos olhos constroem um ponto de origem para raios divergentes, e este ponto de origem serve como a fonte das imagens virtuais, embora os raios de luz não convergam neste ponto. Exemplos de imagens reais e virtuais formadas por uma lente convexa são mostrados na Figura 3. As lentes têm um comprimento característico chamado "distância focal", que é a distância da lente em que os raios de luz originários infinitamente distantes serão focados depois de passar pela lente. Dada a distância focal de uma lente, a distância entre o objeto e a lente determinará a localização da imagem de acordo com a equação da lente fina:

Onde f é a distância focal da lente em metros (m), o é a distância entre a lente e o objeto em metros (m), e eu é a distância entre a lente e a imagem em metros (m). Se a distância do objeto for considerada uma quantidade positiva, então, se a distância da imagem for positiva, a imagem será real e estará localizada na lateral da lente oposta ao objeto. Se a distância da imagem for negativa, a imagem será virtual, ampliada e localizada no mesmo lado da lente que o objeto.
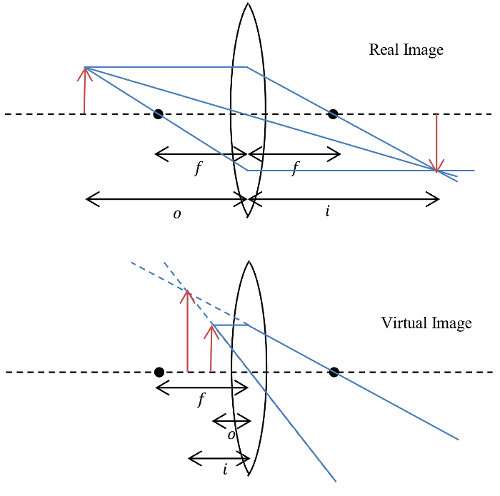
Figura 3: Uma lente convexa produzindo imagens reais e virtuais. Imagens reais se formam a partir da verdadeira convergência de raios de luz. Imagens virtuais são construídas por nossos olhos a partir de raios de luz divergentes.
Procedimento
1. Determine o índice de refração da água usando a Lei de Refração de Snell (Lei de Refração) e encontre o ângulo crítico para reflexão interna total.
- Obtenha um tanque de refração especializado com uma fonte de luz.
- Encha o tanque de refração com água e ligue a fonte de luz. Direcione o feixe da fonte de luz para a metade do tanque cheia de água. Pode ser necessário apagar as luzes da sala.
- Use o prolongador no tanque de refração para medir o ângulo de incidência do feixe (o ângulo medido na metade do tanque cheio de água) e o ângulo de refração (o ângulo medido na metade do tanque cheio de ar) para a interface água-ar no tanque.
- Utilize os ângulos medidos e o índice de refração para ar (nar = 1,00) para calcular o índice de refração da água.
- Repita as etapas anteriores para alguns ângulos de incidente variando de 0° a pouco menos de 90°.
- À medida que o ângulo do incidente é aumentado, nota-se que o feixe de luz refratado não pode mais ser visto na metade do recipiente que contém ar. Gire lentamente a fonte de luz sobre o tanque até que o ponto em que o feixe de luz desapareça pela primeira vez do ar é atingido. Este é o ângulo crítico para a reflexão interna total.
- Se a fonte de luz for ainda mais girada, deve-se observar que o feixe reflete de volta na água.
- Mova a fonte de luz para que o feixe entre na metade do tanque cheio de ar antes de viajar para a água. Regissão alguns ângulos de incidência e refração nesta condição. Note que, anteriormente, o ângulo de incidência era o ângulo em que a luz viajava através da água. Como a luz está agora passando pelo ar primeiro, o novo ângulo de incidência é o ângulo em que ela viaja pelo ar, e o novo ângulo de refração é o ângulo em que ela viaja através da água.
- Observe que a reflexão interna total não ocorre nesta configuração. O reflexo interno total só ocorre quando a luz passa de um meio com alto índice de refração para um meio com menor índice de refração.
2. Meça a distância focal de uma lente e crie imagens reais e virtuais de um objeto.
- Obtenha uma lente convexa, uma lente côncava, uma folha de papel branco, uma régua e um pequeno objeto distinto. Também ajuda ter um banco óptico com suportes para as lentes e objeto, bem como um aparelho para segurar a folha de papel verticalmente.
- Coloque a lente convexa entre o objeto e o pedaço de papel, tudo em uma linha e na mesma altura.
- Mova o objeto e o papel até que uma imagem nítida do objeto apareça no papel. A imagem no papel é uma imagem real.
- Meça a distância da lente para o objeto e a distância da lente para o papel. Use a equação da lente fina para determinar a distância focal da lente.
- Coloque o papel de lado e mova o objeto mais perto da lente até que a distância entre a lente e o objeto seja menor do que a distância focal da lente.
- Olhe através da lente: uma versão ampliada do objeto deve ser vista. Esta imagem é uma imagem virtual.
- Substitua a lente convexa pela lente côncava. Olhe através da lente côncava: agora uma versão desmagnificada do objeto é visível. Esta também é uma imagem virtual.
Resultados
A Lei de Snell dita o ângulo em que a luz será dobrada ao cruzar a fronteira entre dois meios de comunicação. Os ângulos medidos incidentes e refratados na interface água-ar são dados na Tabela 1. Abaixo, um cálculo amostral que dá o índice de refração para a água usando a Lei de Snell é mostrado para um ângulo de incidência igual a 30,1° à medida que a luz vai da água para o ar:
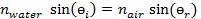
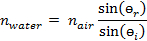

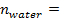 1.33
1.33
O cálculo pode ser repetido para os vários ângulos da Tabela 1, e a média das medidas fornecerá uma medição ainda melhor do índice de refração do que qualquer uma das medidas individuais fornecerá.
Tabela 1: Resultados.
| Interface | ө | ө | nágua |
| Água → Ar | 10.0 | 13.5 | 1.34 |
| Água → Ar | 19.8 | 26.6 | 1.32 |
| Água → Ar | 30.1 | 41.9 | 1.33 |
| Água → ar | 20.1 | 15.1 | 1.32 |
| Água → ar | 44.9 | 32.0 | 1.33 |
| Água → ar | 75.2 | 46.7 | 1.33 |
O ângulo crítico para o reflexo interno total ocorre quando o ângulo de refração é igual a 90°. Para a interface água-ar, a Lei de Snell prevê que o ângulo crítico de incidência é de 48,8°.
Vale ressaltar que o feixe refratário ainda pode ser observado em um ângulo superior a 48,8° ao olhar para a interface em que o feixe de luz passou do ar para a água. É apenas no limite em que o feixe foi da água para o ar que o feixe foi refletido internamente em ângulos superiores a 48,8°. O reflexo interno total só pode ocorrer quando a luz passa de um meio com alto índice de refração para um meio com menor índice de refração.
Para a parte da lente do experimento, quando o objeto foi colocado em cerca de o = 11,02 cm, a imagem entrou em foco em cerca de 9,21 cm. A equação da lente fina então revela a distância focal da lente convexa de cerca de 5,02 cm.
Aplicação e Resumo
Este laboratório explora a física da refração e lentes. A Lei de Snell foi usada para medir o índice de refração da água usando medidas de incidentes e ângulos refratários. Também foi observado o fenômeno da reflexão interna total na interface água-ar. Foi mostrado que as lentes côncavas podem focar a luz e também criar imagens virtuais, permitindo que elas sirvam como dispositivos de ampliação.
O olho humano vê focando a luz na retina, e a visão ruim pode resultar se a luz se concentrar na frente ou atrás da retina. Os óculos ajudam a corrigir a má visão, refocando adequadamente a luz na retina. As câmeras usam uma lente para focar a luz em um sensor da mesma forma que os olhos concentram a luz na retina. Lupas são simplesmente lentes convexas que criam imagens virtuais ampliadas de objetos. Microscópios ópticos usam múltiplas lentes para ampliar imensamente objetos pequenos, como células. Da mesma forma, há um tipo de telescópio chamado refractor que usa lentes para capturar a luz de estrelas, galáxias e outros objetos astrofísicos. A reflexão interna total é usada na maioria das vezes na forma de fibras ópticas, que são utilizadas para transmissão de dados e como fibrascópios.
Pular para...
Vídeos desta coleção:

Now Playing
Reflexão e Refração
Physics II
36.1K Visualizações

Campos Elétricos
Physics II
77.5K Visualizações

Potencial Elétrico
Physics II
104.6K Visualizações

Campos Magnéticos
Physics II
33.4K Visualizações

Carga Elétrica em um Campo Magnético
Physics II
33.7K Visualizações

Investigação Lei de Ohm para condutores ôhmicos e não ôhmicos
Physics II
26.2K Visualizações

Resistores em série e em paralelo
Physics II
33.1K Visualizações

Capacitância
Physics II
43.7K Visualizações

Indutância
Physics II
21.6K Visualizações

Circuitos RC/RL/LC
Physics II
142.8K Visualizações

Semicondutores
Physics II
29.8K Visualizações

Efeito fotoelétrico
Physics II
32.7K Visualizações

Interferência e Difração
Physics II
91.1K Visualizações

Ondas Estacionárias
Physics II
49.8K Visualizações

Ondas Sonoras e Deslocamento Doppler
Physics II
23.4K Visualizações
Copyright © 2025 MyJoVE Corporation. Todos os direitos reservados