Conservation of Momentum

Source: Nicholas Timmons, Asantha Cooray, PhD, Department of Physics & Astronomy, School of Physical Sciences, University of California, Irvine, CA

The goal of this experiment is to test the concept of the conservation of momentum. By setting up a surface with very little friction, collisions between moving objects can be studied, including their initial and final momenta.

The conservation of momentum is one of the most important laws in physics. When something is conserved in physics, the initial value is equal to the final value. For momentum, this means that the total initial momentum of a system will be equal to the total final momentum. Newton's second law states that the force on an object will be equal to the change in the object's momentum with time. This fact, combined with the idea that momentum is conserved, underpins the workings of classical mechanics and is a powerful problem-solving tool.

Momentum is defined as the mass of an object times its velocity  :

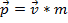. (Equation 1)

One can also define momentum in terms of the forces acting upon an object (Newton's second law):

. (Equation 2)

Here, 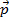is the initial momentum and  is the final momentum, with the same convention used for time and . The sum of the forces acting upon an object is equal to the change in the object's momentum with time. Therefore, if there is no net force acting upon an object, the change in the momentum will be zero. Said another way, in a closed system with no external forces, the initial momentum will be equal to the final momentum.

This concept is most easily understood in the context of one-dimensional and two-dimensional collisions. In one-dimensional collisions, an object with mass and initial velocity collides with another object with mass and initial velocity 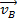. In these collisions, external forces will be assumed to be too small to have an effect. In the lab, an air track is used to reduce the amount of friction, an external force, on the gliders. If the initial momentum is equal to the final momentum, then:

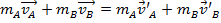, (Equation 3)

where the primed velocities represent that final velocities and the unprimed velocities represent the initial velocities.

Figure 1. Experimental Setup.

1. Understanding the photogate timer.

1. Using a balance, measure and record the mass of each glider.
2. Place one glider on the track with one photogate timer.
3. Set the photogate timer to the "gate" setting.
4. When the glider passes through the photogate, it will record the time at which the flag above the glider passes through the gate. On a return trip, the photogate will not display a new time. Switch the toggle to "read" so that it will display the initial time plus the time of the second pass through the gate.
5. The flag is 10 cm long; determine the velocity of the glider using the fact that the speed is distance divided by time.
6. Send the glider through the photogate several times, including the return trips after it has bounced off the far wall, and measure the velocities in order to become familiar with the equipment. Remember that velocity has a direction. Let the initial velocity direction represent positive and the opposite direction represent negative velocity values.

2. Two gliders of equal mass.

1. Place two gliders and two photogate timers on the track, as in Figure 1.
2. Use Equation 3 to determine the expression for the final velocities. In this part of the experiment, glider B will start from rest.
3. Give glider A some initial velocity so that it will collide with glider B. Record the initial velocity of glider A, as well as the final velocities of each glider. Do this three times, record your results, and compare them to the theoretical prediction.

3. Two gliders of unequal mass.

1. Add 4 weights to glider B, which will double its mass. Repeat steps 2.1-2.3.

4. Equal masses not starting from rest

1. Remove the weights from glider B.
2. Repeat steps 2.1-2.3, but give glider B an initial velocity as well, in the direction of glider A.

Table 1. Results from two gliders of equal mass.

Glider (trial)	(cm/s)	(cm/s)	(cm/s)	(cm/s)	Difference (%)
A (1)	72.5	-0.2	-	-	-
B (1)	0.0	67.1	72.5	66.9	8
A (2)	35.6	0.3	-	-	-
B (2)	0.0	37.4	35.6	37.7	6
A (3)	47.4	0.0	-	-	-
B (3)	0.0	47.8	47.4	47.8	1

Table 2. Results from two gliders of unequal mass.

Glider (trial)	(cm/s)	(cm/s)	(kg cm/s)	(kg cm/s)	Difference (%)
A (1)	52.9	-10.7	-	-	-
B (1)	0.0	37.7	52.9	64.7	22
A (2)	60.2	-13.2	-	-	-
B (2)	0.0	41.5	60.2	69.8	16
A (3)	66.2	-12.0	-	-	-
B (3)	0.0	45.9	66.2	79.7	20

Table 3. Results from equal masses not starting from rest.

Glider (trial)	(cm/s)	(cm/s)	(cm/s)	(cm/s)	Difference (%)
A (1)	48.8	-29.9	-	-	-
B (1)	-42.4	39.8	6.4	9.9	55
A (2)	38.6	-25.2	-	-	-
B (2)	-33.4	32.8	5.2	7.6	46
A (3)	38.9	-43.1	-	-	-
B (3)	-48.5	36.3	-9.6	-6.8	41

The results for steps 2, 3, and 4 confirm the predictions made by Equation 3. In step 2, glider A comes to an almost complete stop after colliding with glider B. Therefore, nearly all its momentum is transferred to glider B. In step 3, glider A does not come to a stop after colliding with the heavier glider B. Instead, it returns in the opposite direction after imparting some momentum unto glider B. In step 4, the total momentum of the system remains the same, despite the direction changes of both gliders. The fact that, in some cases, the total momentum seems to increase and the velocities of both gliders decrease is related to the fact that there is experimental error and the collisions themselves are not completely elastic. Sound and heat given off by the collisions can take energy away from the system. The fact that the air track might not be totally level can change the behavior of the velocities of the gliders. If the track is even slightly inclined, the velocities will increase in that direction due to gravity. The results still show that the total momentum of the system, regardless of initial velocities, remains constant.

   Without momentum conservation, rockets would never leave the ground. Rockets do not actually push against anything-they rely on thrust to lift off. Initially, the fuel of a rocket and the rocket itself are motionless and have zero momentum. When launching, the rocket propels spent fuel out very rapidly. This spent fuel has mass and momentum. If the final momentum must be equal to the initial momentum (zero) then there must be some momentum in the opposite direction of the discarded fuel. Thus, the rocket is propelled upward.

Anyone who has ever fired a gun understands the conservation of momentum. Like the rocket/fuel system from above, the gun/ammunition system also starts at rest. When the ammunition is fired out of the gun at a tremendous speed, there must be some momentum in the opposite direction to cancel out the momentum of the speeding bullet. This is known as recoil and can be very powerful.

The popular desk ornament that consists of several metal balls hanging from strings is called a "Newton's cradle" for good reason. It is another example of the conservation of momentum. When a ball is lifted and released, it strikes its neighbor, transferring its momentum. The momentum travels down the line until the final ball has the momentum of the first, causing it to swing outward. This would go on forever if not for outside forces, such as air resistance and energy loss due to the collisions.

In this experiment, the law of conservation of momentum was verified by considering the collision of two gliders on a near-frictionless track. This fundamental law is perhaps most important because of its power to solve problems. If someone knows the initial momenta, then she knows the final momenta, and vice versa.