Basitleştirilmiş Modeller Kullanılarak Süpersimetri Sınırları Ayarı

Bu kağıt keyfi bir yeni fizik model üzerinde muhafazakar ve saldırgan sınırları içine deneysel basitleştirilmiş bir model sınırlarını yenilenmesi için bir protokol göstermektedir. Kamuya açık LHC deneysel sonuçlar süpersimetri gibi imza ile hemen hemen her yeni fizik model üzerinde sınırları içine bu şekilde değişiklik yapılabilir.

Süpersimetri ve benzeri teoriler deneysel sınırlar, çünkü, çünkü tek noktaların karmaşıklığı muazzam kullanılabilir parametre alan ve genelleme yapmak zor ayarlamak zordur. Onlar daha net fiziksel yorumların var Bu nedenle, daha fenomenolojik, basitleştirilmiş modeller, deneysel sınırlar koyan popüler hale geliyor. Somut bir teori gerçek bir sınır ayarlamak için bu basitleştirilmiş modeli limitlerin kullanımı, ancak, ortaya konmamıştır. Bu kağıt belirli ve tam süpersimetri modeli, minimal süpergraviteden tarihinde sınırları içine basitleştirilmiş modeli sınırlarını yeniden şekillendirdi. Çeşitli fiziksel varsayımlar altında elde Sınırları yönettiği aramalarda tarafından üretilen kıyaslanabilir. Bir reçete ek teorilere muhafazakar ve saldırgan sınırlarını hesaplamak için sağlanmıştır. Çeşitli sinyal bölgelerde olayların beklenen ve gözlenen numaraları ile birlikte kabul ve verimlilik tabloları kullanılarak, LHC deneysel sonuçlar bu ma değişiklik olabilirsüpersimetri gibi imza ile nonsupersymmetric teorileri dahil hemen hemen tüm teorik çerçevenin içine nner.

Standart Model, süpersimetri (SUSY) ^1-14 en umut verici uzantıları biri, CERN'deki LHC deneylerinden birçok aramaların merkezi odak noktası. 2011 yılında toplanan veriler zaten herhangi bir önceki çarpıştırıcısı ^15-22 ötesinde yeni fizik sınırlarını zorlamaya yeterli. Yeni veriler gelmesi ve istisnalar öteye itilmiş olarak, açıkça hariç tutulmuştur geniş süpersimetrik parametre uzayında hangi bölgelerinde fizik toplumunun iletişim kurmak için giderek daha önemli olacaktır. Akım sınırları genellikle sık sık çeşitli kullanılabilir SUSY parametre alanı temsil ve fiziksel kitleler üzerinde limitleri veya dallanma fraksiyonları gibi anlamak zor değil mi kısıtlı, iki boyutlu düzlemlerde, ayarlanır. Basitleştirilmiş modellerin ²³ büyük bir ^{set, 24} bu limitlerin anlamada yardım için önerilmiştir, ATLAS ve CMS hem de bu modellerin çeşitli için dışlama sonuçlar vermiştir ^15-20.

Bu kağıt (aynı zamanda CMSSM olarak bilinen MSUGRA) minimal süpergraviteden ^25-30 örneğini kullanarak tam yeni bir fizik modeli için bu basitleştirilmiş modeli istisnalar uygulamasını göstermektedir. Bu model deneyler ile bağımsız bir şekilde, yayınlanan kişilerce basitleştirilmiş modelleri kullanarak belirlenen sınırlara karşılaştırmak amacıyla seçilir. Prosedür herhangi bir yeni fizik modeli (YKY) için genişletilebilir olduğu kadar geneldir. Bu "döngü" kapatmak ve basitleştirilmiş modellerini kullanarak SUSY sınırları ayarlamak için ilk girişimini temsil etmesi gibi, belirli basitleştirilmiş modellerde sınırları uygulanabilirliği konusunda bazı varsayımlar var teorilere muhafazakar ve agresif sınırlar koyan tarifleri sonuçlanan incelenmiştir LHC deneyleri ile incelenmiştir değil.

Bir UÖM'sine bir sınır ayarı için, üç ayrı operasyon gereklidir. İlk olarak, YKY çeşitli süreden ayıran, kurucu parçalara deconstructed gerekirction modları ve modelde tüm yeni parçacıklar için çürüme modları. İkinci olarak, basitleştirilmiş modeller bir dizi UÖM'sine kinematik ve ilgili olay topolojilerini yeniden seçilmelidir. Üçüncü olarak, bu basitleştirilmiş modellerde mevcut limitleri NPM sınırları üretilmesi amacıyla kombine edilmelidir. Bu üç prosedürler protokolde tarif edilmiştir. Bazı ek yaklaşımlar da olay topolojileri daha geniş bir aralığı için zaten mevcut basitleştirilmiş modelleri uygulanabilirliğini genişletebilir temin edilir.

Tam bir YKY genellikle birçok üretim modları ve birçok olası sonraki bozunur içerir. Kendi bileşenlerine yeni fizik modellerinin yapısöküm ve bu bileşenlerin basitleştirilmiş modeli sınırları uygulaması bir dışlama inşaat doğrudan sınırı sağlar. Herhangi bir sinyal bölge için, en muhafazakar sınır üretim fraksiyonu P kullanılarak ayarlanabilir _{(a, b)} (a, b basitleştirilmiş modeli spa temsil ettiğibasitleştirilmiş bir modele uygun olarak etkinlikleri rticle üretim modu) i ve basitleştirilmiş bir model † tarafından anlatılan şekilde çürümeye üretilen sparticles için dallanma fraksiyonu, BR _{bir → i i →} BR _b x. Bu basit topolojilere, belirli bir sinyal bölgedeki olayların beklenen sayısı daha sonra da yazılmış olabilir

toplamı basitleştirilmiş modeller üzerinde olduğu, σ _tot YKY noktası için toplam kesit olduğunu, L _int aramada kullanılan entegre parlaklık ve _{AE, ben} de basitleştirilmiş modeli olaylar için kabul kat verimliliği _{→ b} Sinyal bölge kabul ediliyor. Bu sayı yeni fizik olaylar t sayısına beklenen% 95 güven düzeyi üst limitine göre olabiliro optimum arama bölgeyi seçin. N% 95 güven düzeyinde hariç yeni fizik olaylarının gözlenen sayısından daha büyük ise model daha sonra bırakılabilir. Onların belirsizliklerin korelasyon hakkında bilgiler mevcuttur örtüşmeyen bölgelerde Dışta kombine edilebilir. Bu bilgiler mevcut değilse, en iyi beklenen sınırı sağlar iyi sinyal bölgesi veya analiz modelini dışlamak girişimi için kullanılan olabilir.

Bu yöntem ile beton sınır inşa etmek için, çeşitli basitleştirilmiş modeller için Aε LHC deneyler ile temin edilmelidir. CMS ve ATLAS hem de çeşitli modeller için Aε ile rakamları yayınladı, ve rakamlar bir kaç HepData veritabanında ³¹ mevcuttur. Tüm bu tabloları yayınlama değerini göstermek için, biz zaten yayınlanmış kıyaslanabilir somut sınırları sağlamak için önemli olduğunu hissediyorum. Bu nedenle kullanmak (ve describİsteğe bağlı bir adım) ATLAS ve CMS dedektörü etkisini taklit hızlı bir dedektör simülasyonu protokolde e. Oldukça iyi Simülasyon türetilen Aε (PGS) ^32, Şekil 1 'de basitleştirilmiş bir model kılavuzunda ATLAS tarafından yayınlanan karşılaştırılır. Bu sonuçlar, daha çok tüm sonuçlar genel olması için beklemek yerine, geri kalan ızgaralarına Aε sonuçlar PGS kullanılarak elde edilmiş ve bu kağıdın geri kalan kısmında doğrudan kullanılan, bu (yaklaşık% 25 olan) birbirine yeterince yakındır. Halka açık basitleştirilmiş bir model Aε sonuçların sayısı arttıkça, bu yaklaşık değerler için ihtiyacı önemli ölçüde azaltılabilir.

İki tutucu varsayımlar sınırı üretim ve çürüme modları daha fazla sayıda ilave edilmesini sağlar. İlk ilişkili üretimi için deneysel Aε en az iki yüksek üretim modları için kötü Aε kadar olmasıdır. Içindahil aramalar, bu genellikle iyi bir varsayımdır. Olayların minimum beklenen sayısı daha sonra olacaktır

İlk toplamı tüm üretim modları üzerinde çalışır, ve sadece bu a ve b basitleştirilmiş modelden tam bu parçacıklar nerede Denklem 1'de yer nerede. Aynı şekilde, farklı bacakları bozunmanın için Aε her iki bacak için kötü Aε gibi en azından yüksek olduğu varsayılabilir. Yani,

her iki tarafında farklı bozunmanın diyagram hemen dahil edilmiştir burada.

İki başka varsayımlar str ayarını sağlayacaksarılığı sınırlar. Bir teoride tüm üretim modları için deneysel Aε basitleştirilmiş modelleri kapsamındaki üretim modları için ortalama Aε benzer varsayabiliriz. Bu durumda, olayların beklenen bir numara yerine olarak yazılmış olabilir

toplamları basitleştirilmiş modellerin kapsamadığı, yalnızca üretim modları üzerinde hem de nerede. Bir başka teoride tüm çürüme modları için Aε basitleştirilmiş modeli topolojilerden kapsadığı etkinlikler için ortalama Aε benzer olduğunu varsayalım olabilir. : O olaylar beklenen sayısı olarak yazılmış olabilir

nerede agasadece basitleştirilmiş modelleri üzerinde çalıştırmak tutarlar. Açıkçası, en agresif MSUGRA sınırı bu varsayımı altında sağlanan ve bu şekilde belirlenen bir sınır, aslında, özel bir arama ile% 95 güven düzeyinde hariç olmaz bölgeler için dışlanma iddia riskleri edilir. Bu iki yaklaşım doğruluğu şüpheli olabilir rağmen basitleştirilmiş modellerin dahil olay kinematik tam SUSY parametre uzay noktasına üstünlügümüz eğer, onlar mantıksız olmayabilir.

† şimdi LHC'de kullanılan bazı basitleştirilmiş modeller ilişkili üretimini içerir. Açıkça Burada ele olmasa da, bu durumda denklem trivially izin vermek için uzatılabilir.

1.. Model Deconstruction

1. YKY'nin parametre uzayında bir uçak kapsayan proton-proton çarpışma olayları oluşturun. Bir parton duş ve hadronization modeli içeren herhangi bir olay jeneratör yapılandırma kullanılabilir. Örneğin MSUGRA durumunda, kütle spektrumları Isasugra ³³ kullanılarak üretilir, ve dallanma fraksiyonlar ve bozunma genişlikleri MSSMCalc ³⁴ kullanılarak hesaplanır. Küçük kütle bölme senaryoları için önemli olabilir matris elemanının ek radyasyon içerir yana olay oluşturma kendisi için, CTEQ 6L1 parton yoğunluk fonksiyonları ile ³⁵ MadGraph 5 1.3.9 ^34, matrix-element olayları üretmek için kullanılır. MSUGRA olayları oluştururken MSUGRA için gelen sipariş jeneratörler LHC deneylerinden seçimlerini taklit etmek için, MadGraph matris elemanına ek bir radyasyon devre dışı bırakılır. Pythia 6.425 ³⁶ sonra, SUSY parçacık (sparticle) çürüme, parton duş için kullanılanve hadronization. Bu programlardan herhangi biri için kapsamlı dokümantasyon web üzerinde kolayca kullanılabilir.
2. , Bir LHC detektörü taklit bir LHC-dedektör parametre kartı ile PGS yoluyla olayları geçmek için. ATLAS ve CMS dedektörü kartları MadGraph 5 ³⁴ ile birlikte arama reach analiz için yeterince iyi performans. Nereye mevcut, kimlik ve performans deneylerinde 'parametrizasyonlari kullanılabilecek bazı analizler ile kamuoyuna açıklandı. İdeal olarak, deneyler, bu direkt olarak kullanılabilir ve bu adım gerekli değildir, bu durumda basit bir modeli ızgaralar, bir dizi için kabul ve verimlilik tam haritaları sağlayacaktır.
3. Hızlı sonuçlarını analiz etmek için, bir ara hafif veri formatı tercih edilir. Jetleri, istikrarlı leptonlar, kayıp enine enerji ve uygun bir biçimde (ExRootAnalysis ³⁴ kullanarak örneğin) PGS çıkışından herhangi diğer gerekli nihai-devlet nesneleri çıkarılıyor tavsiye edilir.
4. Sipariş To, sonuçları sınıflandırmak sparticle üretim ve her olay için çürüme modları sınıflandırmak için gerekli olan jeneratör olay kayıt bölümü ile PGS etkinlik sonuçları ilişkilidir. Bunlara karşılık gelen dallanma oranını hesaplamak edebilmek için tüm parçacık kitleler, üretim mekanizmaları ve çürüme zincirleri yanı sıra kendi sayıları takip edin.
5. Ilgi modeli için mevcut en iyi üretim kesit hesaplamaları hesaplayın. MSUGRA durumunda, gelecek için-giden her noktası için sipariş kesitler CTEQ 6.6 NLO PDF'leri kullanarak NLL-Fast ³⁸ ile Prospino 2.1 ³⁷ kullanılarak hesaplanabilir.

2. Model İmar

1. YKY açık üretim ve çürüme modları en az% 50 kapsayacak şekilde modeli Yapısızlaştırmanın gelen arıza dayanarak, basitleştirilmiş modellerin bir sözlük seçin. Çünkü kütle, kabul Tipik kanalı'nın içinde iki faktörü ile en BSM modellerin hızla düşen kesitinintik olarak deneysel ve kuramsal belirsizlikler içinde olması, bu yeterince yakın hale limiti sadece 20-50 GeV temsil eder. Off-shell/three-body bozunur dahil en direkt çürüme ve bir adım çürüme modelleri, LHC deneyleri tarafından kabul edilmiştir. CMS, tek bir kağıda ²¹ basitleştirilmiş bir model dışlama sonuçları bir dizi topladı. ATLAS ve CMS ikisi de ağır lezzet basitleştirilmiş modelleri bir dizi kabul var. Modellerinin tam listesini tek bir yerde kamuya açık yapılmamıştır. Ancak, sonuç iki deney 'kamu web sayfalarında ^{39, 40} mevcuttur. Bu NPM'nin yeniden inşası için seçili olmalıdır basitleştirilmiş modellerdir.
2. Bu noktaya yeniden oluşturmak için kullanılan basitleştirilmiş modelleri kaynaklananlar ile birkaç temsili NPM noktalarının kinematik karşılaştırma, basitleştirilmiş bir model içerisinde kalitesini test etmek amacıyla. Belirli bir YKY noktası için, ile ilgili basitleştirilmiş modellerini inşaUygun kitleler.
3. O model tarafından temsil çürüme için bu basitleştirilmiş modeli kez dallanma fraksiyonu temsil üretim fraksiyonu içerir her model türüne ağırlık atayın.
4. Ilişkili üretim için, sadece çift-üretim basitleştirilmiş modelleri düşünülürse, iki ilgili basitleştirilmiş model arasındaki ağırlık bölmek.
5. Bu grup benzer üretim ve çürüme-modları için YKY olay topolojilerle fiziksel-motive sadeleştirmeler bir dizi uygulanması tavsiye edilir.
6. Birlik tüm basitleştirilmiş modeller için ağırlıkların toplamı normalleştirmek.
7. Bir önceki protokol açıklanan olay oluşturma prosedürü kullanılarak Örnek NPM noktaları için kinematik dağılımları hesaplayın.
8. Tipik sinyal seçimleri sonrasında YKY noktanın kinematiği birleşik basitleştirilmiş modellerin olanlardan (% 30) σ daha fazla olursa, üretim ve çürüme geliştirmek için ek basitleştirilmiş modelleri içerirfaz uzayı kapsama. % 15 seviyesinde farklılıklar için çoğu yeni fizik modeller hızla düşen enine kesitlerin son dışlama sonuçlar üzerinde göz ardı edilebilir bir etkiye sahiptir.

3. İnşaat sınırlayın

1. Mevcut ve ilgili Aε ve uygulanabilir her deneysel sinyal bölgede kabul ediliyor basitleştirilmiş modelleri için yeni fizik olayların sayısı% 95 güven seviyesi üst limiti edinin.
2. (Varsa) varsayımlar nokta hariç hangi altında belirlemek için her bir parametre uzay noktada ilgi UÖM'lere Denklemlerini 1 ve 3-5 uygulayın.
3. Bölgeler düzgün ‡ kombine edilebilir, böylece sinyal bölgelerin plan belirsizlikler arasında korelasyon mevcut olmadıkça, en iyi beklenen performansı ile sinyal bölgeye göre belirlenen limiti kullanın.
4. Önceki protokol ve dışlama kontür yayılması ile yapılan kinematik karşılaştırma ile, ra belirlemekhücumdan hangi deneysel dışlama yalan gerekir.

‡ Şu anda, böyle bir korelasyon mevcuttur.

MSUGRA, çıktı bir arıza parametre uzayda bir noktaya modeli yapısöküm adımı uygulanan olması en uygun oluşturulan bütün olay için çeşitli üretim ve çürüme modları yukarı sayma ve ilgili üretim oranları komplo ve kesirler dallanma tarafından görüntülenmiştir rölatif frekanslar. Örnek MSUGRA puan için çeşitli üretim ve bozunma modları için dallanma oranı, Şekil 2 ve 3 de gösterilmiştir. SUSY parametre uzayda diğer noktaları için benzer rakamlar çok sayıda online ⁴¹ bulunmaktadır.

Şekil 4'te gösterildiği gibi MSUGRA durumunda, faz alanı boyunca bazı eğilimler, mevcut bulunmaktadır. Skuark üretim düşük m _0, yüksek m _1/2 bölgesinde hakim ve gluino üretim yüksek m _0, düşük m _1/2 bölgesinde hakimdir. Bölgedeskuark üretim hakim olduğu, doğrudan skuark hafif süpersimetrik parçacık (LSP) zayıflar tercih edilmektedir. Gluino üretim hakim Ancak LSP için gluino doğrudan bozunmaktadır toplam bozunma faz alanı ~% 30 daha fazla ihtiva hiç bölgelerde. Asılır bölgede, doğrudan chargino üretim özellikle yüksek m ₀ ve squarks ve Gluinolar tüm ağır olan yüksek m _1/2 doğru, bir nonnegligible katkı yapar. Bu MSUGRA uçak, bu nedenle, beş basitleştirilmiş modeli (SM) senaryoları ile kaplı olabilir:

• Doğrudan bir kuark (SM 1) emisyonu yoluyla LSP için çürümeye squarks çifti üretim;
• Doğrudan iki kuark (SM 2) emisyonu yoluyla LSP için çürümeye Gluinolar çifti üretim;
• Squarks Pair-üretim, LSP bir adım hangi çürüme. Skuark bir kuark emisyon yoluyla chargino zayıflar ve chargino bir W-Boso emisyon yoluyla LSP bozunur n (SM 3);
• Gluinolar Pair-üretim, LSP bir adım hangi çürüme. Gluino iki kuark emisyon yoluyla chargino zayıflar ve chargino bir W-bozonu (SM 4) emisyonu yoluyla LSP bozunur ve
• Doğrudan W-bozonu (SM 5) emisyonu yoluyla LSP için çürümeye charginos çifti üretim,.

Bu beş basitleştirilmiş modelleri birine ait olarak sınıflandırılan MSUGRA olayların fraksiyon, Şekil 5'te gösterilmektedir. MSUGRA Örneğin, aşağıdaki ek basitleştirilmesi yaklaşımları yapılır: skuark gluino O'a indiğinde, gluino çürüme olay topoloji sınıflandırmada sayılır ve gluino için skuark çürüme durumunda ek bir jet olarak sayılır ("artı jetler"), bu başlangıç ​​ya da son-devlet radyasyon aynıydı sanki. Gluino bir skuark aracılığıyla bozunduğundailes/ftp_upload/50419/50419gtilde.jpg 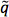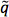"/> → q , → q gluino iki jetleri üretilen ve doğrudan çürümüş sanki Ancak, çürüme son devlet hala skuark adım atlama, görünür, Kinematikte bazı (küçük) farklılıkları kaydedin. Gluino hiçbir ara skuark ile kuark bir çift emisyon yoluyla çürümüş sanki bu durumlarda, bu nedenle, bozunum zinciri (sınıflandırılır → qq ), Yerine bir ile skuark çürüme olarak sınıflandırmak dahaek başlangıç ​​veya son-devlet radyasyon gibi jet ( 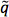→ q artı jet (ler)). İlişkili skuark-gluino üretim skuark ve gluino basitleştirilmiş modelleri arasında eşit olarak bölünür. Bu yaklaşımlar ile, söz konusu beş basitleştirilmiş modellerinden biri olarak SUSY olayların büyük bir kısmını sınıflandırmak mümkündür. Bu modeli yeniden yolunda ilk adımdır.

İki MSUGRA parametre alanı noktaları için olay kinematik onları taklit etmek için kullanılan basitleştirilmiş modelleri bir kombinasyonu ile birlikte, Şekiller 6, 7 ve 8 de gösterilmiştir. Bu iki nokta, yukarıda anlatılan yöntem kullanılarak deconstructed edilir ve seçilen beş basitleştirilmiş modelleri, kütle spektrumları, üretim oranlarına göre inşa edilmiş ve birleştirilir, venoktalarına fraksiyonlarını dallanma. Basitleştirilmiş modeli olaylar MSUGRA olaylara benzer bir şekilde üretilir ve analiz edilmiştir. Burada, LHC süpersimetri aramalarda kullanılan anahtar kinematik değişkenlerin dört gösterilmiştir: önde gelen jet enine ivme (p _T), lepton p _T, kayıp enine enerji ve etkili kitle, enine momenta dört önde gelen skaler toplamı olarak tanımlanan jetleri ve lepton. İki özellik jet gelen ve enine enerji dağıtımında eksik, güçlü üretim ve weakino üretimine karşılık gelen etkin kitle görebilir. Bu kapsayıcı dağıtımlarında, bazı tutarsızlıklar açıkça görülebilir. Düşük-p _T lepton kuyruk, örneğin, basitleştirilmiş modellerin herhangi kapsamında değildir tau bozunmanın ağırlıklı olarak bir. Düşük eksik enine enerji, düşük etkili kitle bölge modellenmiştir değildir LSP-X ilişkili üretim, kısmen olduğunu. En kinematik özellikleri açıklanmıştırHızla düşen geçmişi olan bir parametre uzayda bir arama amaçları için PGS tarafından yeterince iyi. Tau sahte oranları tau analiz sonuçlarının bir parametrelendirilmesinde için önemli bir sorun olmaya devam etmektedir ve tamamen bu sorunu ele alan bu protokol kapsamı dışındadır.

Bununla birlikte, LHC'de kullanılan çoğu sinyal bölgelerin keser basit bozunma topolojisi daha karmaşık, genellikle yumuşak ya da daha yüksek çeşitlilik olaylar üzerinde seçilir şekildedir. Böylece, sinyal bölge seçimi basitleştirilmiş modelleri tarafından olay kinematiğinin açıklamasını geliştirmek eğilimindedir. Yeni bir ara ATLAS SUSY ¹⁶ 'de kullanılana benzer bir tek lepton bölgesinde karşılaştırması Şekil 7 ve 8 de gösterilmiştir. Şekil ve kuyrukları hem de anlaşma önemli ölçüde daha iyidir. Basitleştirilmiş modeller için kinematik tam SUSY noktası için verimlilik ve kabul de tarif edilebilir düşündüren, kapsayıcı SUSY modeli kinematiğine iyi karşılaştırmakbasitleştirilmiş modelleri sınırlı bir kombinasyonu ile. Tabii ki, basitleştirilmiş modeller tarafından açıklanan topolojilerle gelen sadece bu SUSY olayların kinematik kendi basitleştirilmiş modeli meslektaşları aynıdır. Bu, bu basitleştirilmiş modellerin kapsamadığı bu olayların toplam olaylara veya kapalı olanlar için kinematik benzer küçük bir kısmını ya da olduğu bir teyidi olarak hizmet vermektedir. Bu MSUGRA durumunda modeli yeniden adım tamamlar.

Bölüm 3 uyarınca sınır belirleme prosedürü sonra, = 10 tan β ile MSUGRA düzlemine uygulanır A = 0 ₀ ve> 0 μ, ATLAS sıfır-lepton arama ¹⁶ sinyal bölgeleri kullanarak. Beş sinyal bölgelerinde bu aramaya dahil edilir ve en iyi beklenen limiti ile sinyal bölgesi her bir nokta için kullanılır. En iyi sinyal bölgesinde beklenen SUSY olayların sayısı, gözlenen% 95 güven seviyesini aşarsa bir nokta dışında olduğu düşünülmektedirbu sinyal bölgede yeni fizik olaylar üzerine üst sınır. Şekil 9, daha önce ele alındığı gibi, basitleştirilmiş bir model dışlama sonuçları sinyaline sistematik belirsizlikler olmadan sıfır lepton dışlama karşılaştırılır. Dört basitleştirilmiş modeli dışlama eğrileri Denklem 1 ve 3-5 karşılık gösterilmiştir. Sıfır-lepton dışlama sınırı karşılaştırıldığında, en muhafazakar basitleştirilmiş-model-tabanlı yaklaşım hakim bölgede oldukça kötü yapar 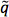ve weakino üretim ilişkili ~ 100 GeV varan doğru sınırını eksik. Bu, (Şekil 3'te açık modları sayıda cf) nedeniyle gluino nispeten karmaşık çürümeye kısmen aynı zamanda. 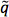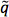Kapsama gerçek sınırına çok yakınhakim bölge için ve üretimi, bunun için basitleştirilmiş bir model türetilmiş sınırı gerçek limitinin 40 GeV'e içindedir.

Bu reçete sinyal modeli üzerine teorik belirsizliklerin tedavi atlar. Aslında, LHC deneyleri şu anda tutarlı bir şekilde bu belirsizlikleri tedavi yok, ne belirsizlikler tüm dahildir. Resim deney, örneğin, GUT ölçek parametrelerden görülebilir kütleler hesaplanırken herhangi bir belirsizlik bulunmaktadır. Inci sınırlarıBurada sunulan, bu nedenle, yayınlanmış sınırların farklılık beklenmelidir. Şekil 10'da ise, sıfır lepton kanalında yayınlanan ATLAS dışlama sınırı sinyali üzerinde herhangi bir sistematik bir belirsizlik olmaksızın Burada elde edilenlere karşılaştırılmıştır. Sinyal belirsizlikler olmadan sınırı yayınlanan sınırı açıkça daha yüksektir. Kağıdın geri kalanı için, sinyal üzerinde sistematik belirsizlikler olmadan sınır basitleştirilmiş modellerini kullanarak ulaştı gereken "doğru cevap" olarak alınacaktır. Teorik belirsizlik aynı şekilde hem de ilave edilebilir ve yaklaşık olarak aynı şekilde her iki sınır etkileyecektir.

Olabildiğince doğru olarak mevcut kaynaklar ile sonuçlar elde tasvir için, basitleştirilmiş modeli noktaları zaten ATLAS deneyinde ¹⁷ tarafından kullanılmakta olduğunu kabaca gelen bir ızgara oluşturulur. Bu nokta arasında, Aε iki boyutlu m enterpolasyonlananskuark / m _gluino = m _LSP grid. Bu deneyler tam üç boyutlu Aε sağlayacak olası değildir, çünkü SM 3 ve SM 4 üç boyutlu ızgaralar, ve çünkü, ara chargino kütlesinin üç değerler kullanılır: m _chargino = x × (m _{skuark / gluino} - m _LSP) + m _LSP, x = 0.25, 0.5 ve 0.75. Bu üç iki boyutlu düzlem arasındaki katmak için basit bir kuadratik formda kullanılır. M _LSP = m _chargino ve m _{skuark / gluino} sınırlarını yaklaşırken, çürüme modları doğal olarak daha karmaşık interpolasyon gereksiz hale kapatın.

Dışlama eğrileri karşılaştırılarak, bir kimse gerçekten muhafazakar bir dışlama sınırı Denk kullanarak ayarlayabilirsiniz görebilirsiniz. 1 basitleştirilmiş modu tarafından iyi kaplıdır faz uzayında bölgelerde oldukça iyi "doğru" dışlama sınırı izlerls (cf Şekil 5). De Eşitlik, kapsamında değildir bölgelerde. 3. hala muhafazakar bir sınır sağlar. Agresif sınır Denk ayarlayın. Uzun gluino çürüme zincirleri olduğu varsayımı ve kısa zincirleri tarafından iyi modellenmiştir çünkü 5, skuark egemenliğindeki bölgede ve faz uzayı gluino egemenliğindeki bölgede 100 kadar GeV tarafından 40 GeV tarafından dışlanma overestimates basitleştirilmiş modeller bazı düzeyinde geçersiz. Parametre uzay kapsamı,% 20 örtü altı muhafazakâr sınırlar, örtü altı% 10, orta iki sınırları ve aşırı kapaklar% 10 agresif limiti açısından. Doğal olarak, mevcut basitleştirilmiş modellerin sözlüğü genişleyen muhafazakar limitini artırmak ve daha doğru Aε gibi agresif sınırını azaltacaktır daha fazla üretim ve çürüme modları için dahildir. Ancak, hatta basitleştirilmiş modelleri bu küçük bir sayı ile, muhafazakâr sınırlar kümesi "düzeltmek" sonucu yakındır.

Demonstrasyon amaçlı, limitleri de yüksek tan β bir MSUGRA sinyal bölgeye yerleştirilir. Bu sınırlar, Şekil 11 'de gösterilmiştir. Şekil 10 gözlenen anlaşmaya dayanarak, deneysel dışlama biraz Denk tarafından belirlenen dışlanma ötesine durmalıdır. 3.

Daha egzotik teorileri genelleştirerek, hatta teoriler susy basitleştirilmiş model küçük bir liste uygulanabilirliğini genişleyen, çeşitli yaklaşımları yapılabilir:

1. Bu ağır lezzet jetleri lezzet tagging yok aramalar için hafif lezzet jetleri ile aynıdır;
2. Fotonlar fotonları tespit yok aramalarda jetleri aynı olduğunu;
3. Yani yarısından fazlası zaman, chargino (neutralino) gluino işlevsel özdeş bir imza iki kuark emisyon yoluyla bozunur üreten bir W-bozonu (Z-bozonu) emisyon yoluyla LSP bozunur.

Şekil 1. Sol, ATLAS üç jet "gevşek" bir lepton sinyal bölgesi ¹⁷ için kamu Aε. Doğru, burada kullanılan MadGraph + Pythia + PGS kurulumunda yeniden aynı. Bazı farklılıklar burada kullanılan farklı jeneratörler ve yüksek istatistiklerinden beklenemez, ama iki birbirlerine yakından izleyin. büyük rakam görmek için buraya tıklayın .

19/50419fig2highres.jpg "src =" / files/ftp_upload/50419/50419fig2.jpg "/>
Şekil 2. SUSY üretim mekanizmaları ve MSUGRA parametre uzayında çürüme modları için oranları dallanma. Üst satır (m ₀ = 300 GeV, m _1/2 = 600 GeV tan (β) = 10, A ₀ = 0 GeV ve> 0 μ ) skuark üretimin egemen olduğu parametre uzayda bölge için tipik olan ve alt satır (m ₀ = 1,000 GeV, m _1/2 = 350 GeV tan (β) = 10, A ₀ = 0 GeV ve μ > 0) iki uç arasında uzanan bir miktar parametre alanı bölge için tipiktir. Kendi dallanma fraksiyonu% 0.5 'den daha büyük ise, netlik sağlamak için, üretim ve çürüme modları yalnızca listelenir. Bir dizi etiketleri "SM" modeli yeniden protokol tartışılan basitleştirilmiş modeller için uygun çürüme modları verilir.les/ftp_upload/50419/50419fig3large.jpg "target =" _blank "> büyük rakam görmek için buraya tıklayın.

Şekil 3.. SUSY üretim mekanizmaları ve MSUGRA parametre uzayında çürüme modları için oranları Branching. Üst satır (m ₀ = 300 GeV, m _1/2 = 500 GeV tan (β) = 25, A ₀ = 1.500 GeV ve μ> 0) skuark üretimin egemen olduğu parametre uzayda bölge için tipik olan ve alt satır (m ₀ = 2.100 GeV, m _1/2 = 100 GeV tan (β) = 45, A ₀ = 500 GeV ve μ> 0) gluino üretimin egemen bölge için tipiktir. Anlaşılır olması için, üretim ve çürüme modları sadece yer olup olmadığınıkendi dallanma fraksiyonu% 0.5 'den daha büyüktür. Bir dizi etiketleri "SM" modeli yeniden protokol tartışılan basitleştirilmiş modeller için uygun çürüme modları verilir. Beyaz bölgelerde modeller sınırlı Monte Carlo istatistiklerle, basitleştirilmiş modeller tarafından açıklanan hiçbir olay yoktu. büyük rakam görmek için buraya tıklayın .

Şekil 4. Tan (β) ile MSUGRA parametre uzayında ana SUSY üretim ve çürüme modları yüzde dallanma oranları, değişimi 10, A ₀ ve μ> = 0. Güçlü sparticles olan sağ üst köşesinde, ağır, önemli bir Contr içerir weakino üretimden ibution. Beyaz bölgelerde modeller sınırlı Monte Carlo istatistiklerle, basitleştirilmiş modeller tarafından açıklanan hiçbir olay yoktu. büyük rakam görmek için buraya tıklayın .

Şekil 5. Düşük-tan (β) için, bu çalışmada dikkate beş basitleştirilmiş modellerinden birine ait olarak sınıflandırılan MSUGRA olayların yüzdesi (solda) ve yüksek tan (β) (sağ). büyük rakam görmek için buraya tıklayın .

419fig6highres.jpg "src =" / files/ftp_upload/50419/50419fig6.jpg "/>
Şekil 6. Bir skuark-üretim-egemen MSUGRA noktaya (m ₀ = 300 GeV, m _1/2 = 600 GeV tan (β) = 10, A ₀ = 0 GeV ve μ> 0) ve bir dizi kinematiği Beş basitleştirilmiş modeller, üst soldan aynı kütle spektrumu. Yönünde ile jet p _T lider, muon p _T, etkili kitle lider ve enine enerji eksik inşa. Hiçbir sinyal seçimi tatbik edilmiştir. büyük rakam görmek için buraya tıklayın .

Şekil 7. Bir skuark-süreden KinematiğiCustomer Interaction-egemen MSUGRA noktası (m ₀ = 300 GeV, m _1/2 = 600 GeV tan (β) = 10, A ₀ = 0 GeV ve> 0 μ) ve beş basitleştirilmiş modellerin kümesi aynı kütleye kullanılarak inşa spektrumu. saat yönünde sol üst, lider jet p _T, önde gelen muon p _T, etkin kütle ve eksik enine enerji. Tek-lepton dört jet "sıkı" ATLAS SUSY arama benzer bir sinyal seçimi tatbik edilmiştir. büyük rakam görmek için buraya tıklayın .

Şekil 8. Karmaşık MSUGRA noktanın kinematiği (m ₀ = 1,000 GeV, m _1/2 =350 GeV tan (β) 10, A ₀ = 0 = GEV ve μ> 0) ve beş basitleştirilmiş modellerin kümesi, üst soldan aynı kütle spektrumu. Yönünde ile jet p _T lider, muon p _T önde inşa , etkin kütle, ve eksik enine enerji. Tek-lepton dört jet "sıkı" ATLAS SUSY arama benzer bir sinyal seçimi tatbik edilmiştir. büyük rakam görmek için buraya tıklayın .

Şekil 9,. Dışlama sınırı ile karşılaştırıldığında = 10 tan β, A ₀ = 0 ve μ> 0 (10a) ile MSUGRA modeller için sıfır lepton hariç bırakma sınırlı Kombinebasitleştirilmiş modeller kullanılarak elde sadece (10b). iyi beklenen sınırını sağlayan sinyal bölgesi parametre uzayında belirli bir noktası için alınır. Beklenen% 95 güven düzeyi sınır kesikli mavi çizgi olarak gösterilir, ve gözlenen sınır katı bir kırmızı çizgi olarak gösterilir. Bu sınırların bazıları biraz farklı parametre seçenekler kullanılarak üretilmiş olmasına rağmen önceki aramalardan sonuçları da karşılaştırma amacıyla ^42-48 için gösterilmiştir. Basitleştirilmiş modeli limitleri ana metninde sınır denklemlere karşılık varsayımlar dört farklı setleri kullanılarak üretilir. büyük rakam görmek için buraya tıklayın .

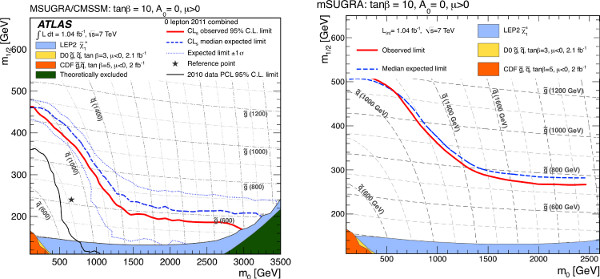
Şekil 10. Kombine sıfır lepton dışlama sınırları= 10 tan β, PGS kullanılarak elde edilen dışarıda bırakma limiti bulunan ve sinyal üzerinde sistematik belirsizlik olmaksızın karşılaştırıldığında (sol) A ₀ = 0 ve μ> 0 ¹⁶ ile MSUGRA modelleri. Sinyal bölgesi en beklenen sınırı sunan bir alınır parametre uzayında puan verilir. Beklenen% 95 güven düzeyi sınır kesikli mavi çizgi olarak gösterilir, ve gözlenen sınır katı bir kırmızı çizgi olarak gösterilir. Bu sınırların bazıları biraz farklı parametre seçenekler kullanılarak üretilmiş olmasına rağmen önceki aramalardan sonuçları da karşılaştırma amacıyla ^42-48 için gösterilmiştir. büyük rakam görmek için buraya tıklayın .

FiGüre 11. = 40 tan β ile MSUGRA modeller için Dışlama limitleri, A ₀ = -500 GeV ve μ> 0 (solda) ve tan = 20 β, A ₀ = 500 GeV ve> 0 μ (sağda) basitleştirilmiş modeller kullanılarak elde edilen tek . Kombine sınırları parametre uzayda her noktada en iyi beklenen sınırını oluşturur sinyal bölgesini kullanılarak elde edilir. Basitleştirilmiş modeli limitleri ana metninde sınır denklemlere karşılık varsayımlar dört farklı setleri kullanılarak üretilir. büyük rakam görmek için buraya tıklayın .

Tamamen yeni bir fizik modelinde bir dışlama konturu üretilmesi için basitleştirilmiş bir model sınırlarının uygulanması gösterilmiştir. MSUGRA parametre alanı noktalarının belirgin karmaşıklığına rağmen, kinematik basitleştirilmiş modelleri sadece küçük sayıda bir kombinasyonu ile iyi çoğaltılabilir. Belirli bir sinyal bölgede bakarken bugüne kadar LHC'de yapılan aramalar yüksek p _T nesneleri (nispeten) az sayıda basitleştirilmiş model gibi olay topolojilerini lehine eğilimindedir beri kinematik anlaşma daha artırıldı.

Basitleştirilmiş modellerinden türetilen dışlanma kontür zaten özel aramalar ile yayınlanan bu olumlu ile karşılaştırma. Bu işlem ile, o trivially daha egzotik SUSY teorileri, hatta basitleştirilmiş modellerin kapsamadığı imzaları ile nonSUSY teorileri içine içine dışlama sonuçları değişiklik mümkündür. Bu yöntem, ilave olarak, veri a korunması için basit bir yol sağlar:nd gelecek teorileri mevcut arama uygulaması.

Pratik olarak, bu yaklaşım, LHC deneyleri ve LHC teorisyenler ve görüngübilimcilerin için büyük bir yarar için tasarruf önemli bir kaynak anlamına gelir. Bilgi matris elemanı ve çürüme olasılıklar mevcuttur kullanarak teorileri recasting ile, modelin hiçbir işlem-yoğun simülasyonu yapılmalıdır. Ama tamamen kapsamında olmayabilir - - basit nihai devlet imzaların yerine, deneyler delikanlı içeren teorik modellerin büyük bir çeşitlilik dışlama sonuçlar sağlamak için ücretsizdir. Benzer şekilde, teorisyenleri LHC deneyleri kendi tercih modeli sınırlarını üretmek için beklemek gerekmez. Basitleştirilmiş modeller basitleştirilmiş modelleri nispeten az sayıda olan bir model, tüm üretim ve çürüme modları, kapak olmayabilir, ancak bu olasılıklar oldukça geniş bir yelpazede karşılamak mümkündür. Bu şekilde edinilen istisnalar doğrusu tam deney sonuçlarını örtüşmemektedirzihinsel arama. Geçerli LHC arama dönemde, ancak, teori alanı zaten zaten yapılan aramalarda tarafından dışlanmış ne kadar kritik ve şaşırtıcı derecede doğru tahmin verir ve ne kadar hala keşif açık olabilir.

Yazarlar hem ATLAS İşbirliği üyeleridir. Ancak, aksi takdirde hiçbir ATLAS iç parasal kaynaklar, ya da, bu çalışmanın tamamlanması kullanılmıştır.

Yazarlar basitleştirilmiş modelleri ve potansiyel tuzaklar önemli tartışma Jay Wacker'la teşekkür etmek istiyorum. Yapıcı eleştiri ve cesaret gerekli olduğu zaman için de Max Baak ve Eifert Till çok teşekkürler. Bu işbirliği mümkün yapmak için CERN Yaz Öğrenci Programı sayesinde.