단순화 된 모델을 사용하여 초대칭에 대한 제한 설정

이 논문은 임의의 새로운 물리 모델에 대한 보수 및 적극적인 한계에 실험 단순화 된 모델의 한계를 개주를위한 프로토콜을 보여줍니다. 공개 LHC 실험 결과는 초대칭 같은 서명 거의 모든 새로운 물리 모델에 대한 제한으로이 방식으로 재조명 할 수 있습니다.

초대칭과 유사한 이론에 대한 실험적인 한계 때문에 때문에 단일 지점의 복잡성의 거대한 가능한 매개 변수 공간과 일반화하기 어려운 설정하기가 어렵습니다. 그들은 명확한 물리적 해석을 따라서, 더 많은 현상 학적, 단순화 된 모델은 실험의 한계를 설정하는 인기를 끌고있다. 구체적인 이론에 실제의 한계를 설정하는 이러한 단순화 된 모델 한계의 사용은, 그러나, 증명되지 않았다. 이 논문은 특정하고 완전한 초대칭 모델, 최소한의 supergravity에 대한 제한으로 단순화 된 모델의 한계를 재조정 할. 다양한 물리적 가정에서 얻을 수 제한은 직접 검색에 의해 생성 된 것과 비교할 수 있습니다. 처방전은 추가 이론에 보수적이고 적극적으로 제한을 계산하기 위해 제공됩니다. 다양한 신호 지역에서 이벤트의 예상 및 관찰 번호와 함께 수용과 효율성 테이블을 사용하여, LHC 실험 결과는이 엄마의 개작 할 수 있습니다초대칭 같은 서명 nonsupersymmetric 이론을 포함하여 거의 모든 이론적 프레임 워크에 nner.

표준 모델, 초대칭 (SUSY) ^1-14의 가장 유망한 확장 기능 중 하나는 CERN의 LHC 실험을 통해 많은 검색의 중앙 초점이다. 2011에서 수집 된 데이터는 이미 이전 인 LHC ^15-22의 것 이상의 새로운 물리학의 한계를 극복하기에 충분하다. 새로운 데이터가 도착 제외가 멀리 계속 밀려, 그것은 명확하게 제외 된 다양한 초대칭 매개 변수 공간의 어떤 영역 물리학 커뮤니티에 의사 소통을 점점 더 중요 할 것이다. 전류 제한은 일반적으로 자주 다양한 사용할 수 SUSY 매개 변수 공간을 나타내는 물리적 대중에 대한 제한 또는 분기 분수로 이해하기 어려운없는 제약이 두 가지 차원 평면에 설정됩니다. 단순화 된 모델 ^(23)의 대형 ^{세트 (24)는} 이러한 제한의 이해를 돕기 위해 제안되었으며, ATLAS와 CMS는 모두이 모델의 몇 가지에 대한 배제의 결과를 제공 한 ^15-20.

이 논문은 (또한 CMSSM로 알려진 MSUGRA) 최소 supergravity ^{25 ~ 30의} 예제를 사용하여 전체 새로운 물리 모델이 단순화 된 모델 제외의 응용 프로그램을 보여줍니다. 이 모델은 실험에 의해 독립적으로 발행에게 단순화 된 모델을 사용하여 설정 한계와 비교하기 위해 선택된다. 절차는 새로운 물리 모델 (NPM)로 확장 할 수 있도록 충분히 일반적이다. 이 "루프를 닫습니다"단순화 된 모델을 사용하여 SUSY에 대한 제한을 설정하는 첫 번째 시도를 나타냅니다으로, 특히 단순화 된 모델에 대한 제한의 적용 가능성에 대한 가정의 수는이 이론에 보수적이고 적극적으로 제한을 설정하는 조리법의 결과로, 탐구하는 LHC 실험에 의해 조사되지.

NPM에 제한을 설정하는 경우, 별도의 세 가지 작업이 필요합니다. 첫째, NPM은 다양한 produ의 분리, 그 구성 부분으로 해체해야ction의 모드와 모델의 모든 새로운 입자의 붕괴 모드. 둘째, 단순화 된 모델의 집합 NPM의 운동학 및 관련 이벤트 토폴로지를 다시 선택해야합니다. 셋째, 이러한 단순화 된 모델에 가능한 한계는 NPM 한계치를 생성하기 위해 결합한다. 이 세 가지 절차는 프로토콜에 설명되어 있습니다. 몇몇 추가 근사치는 이벤트 토폴로지의 넓은 범위에 이미 이용 가능한 단순화 모델의 적용을 확대 할 수가 제공된다.

전체 NPM은 일반적으로 많은 생산 모드와 여러 가지 후속 붕괴를 포함한다. 해당 구성 요소에 새로운 물리 모델의 해체 및 그 구성 요소에 단순화 된 모델 제한의 적용 제외의 건설을 직접 제한 할 수 있습니다. 어떤 신호 지역의 경우, 가장 보수적 인 한계는 생산 분수 P를 사용하여 설정할 수 있습니다 _{(A, B)} (A, B는 단순화 된 모델의 스파를 나타냅니다단순화 된 모델과 동일한 이벤트 인 rticle 생산 모드) i와 단순화 된 모델 †에서 설명하는 방법으로 부패에 대한 생산 sparticles의 분기 부분, BR _{→이 나는 →} BR의 _B를 x. 이러한 간단한 토폴로지에서 주어진 신호 지역 이벤트의 예상 수는 다음과 같이 쓸 수있다

합이 단순화 된 모델에이고, σ _{어린 아이가} NPM 지점의 총 단면이며, L의 _INT는 검색에 사용되는 통합 광도이며, _{AE, 내가있는} 단순화 된 모델 이벤트에 대한 수용 배 효율이다 _{→ B} 신호 영역을보십시오. 이 번호는 새로운 물리 이벤트 t의 개수에 예상 95 % 신뢰 수준의 상한과 비교 될 수있다O 최적의 검색 영역을 선택합니다. N은 95 % 신뢰 수준에서 제외 된 새로운 물리 이벤트의 관측 된 수보다 큰 경우 모델은 배제 할 수있다. 그들의 불확실성의 상관 관계에 대한 정보가 사용 가능한 경우 겹치지 않는 지역에서 제외가 결합 될 수있다. 이 정보를 사용할 수없는 경우에, 최고의 예상 한계를 제공 최상의 신호 영역 또는 분석 모델을 제외하도록 시도 할 수있다.

이 방법에 대한 구체적인 제한을 구성하기 위해, 여러 가지 단순화 된 모델에 대한 Aε는 LHC 실험을 통해 사용할 수 있어야합니다. CMS와 ATLAS는 모두 몇 가지 모델에 대한 Aε와 수치를 발표했으며, 수치의 약간은 HepData 데이터베이스 ^(31)에 사용할 수 있습니다. 그러한 모든 테이블 출판의 가치를 입증하기 위해, 우리는 이미 발행 견줄만 구체적인 제한을 제공하는 것이 중요하다 느낀다. 따라서 우리가 사용하는 (그리고 describ선택적 단계) ATLAS 또는 CMS 검출기의 효과를 모방하는 빠른 검출기 시뮬레이션과 같은 프로토콜의 전자. 약간의 시뮬레이션에서 파생 된 Aε은 (PGS) ^(32)는 그림 1에 단순화 된 모델의 격자 ATLAS 발행에 비해됩니다. 이러한 결과는 오히려 모든 결과가 공개 될 때까지 기다리 이상, 나머지 그리드 Aε 결과는 PGS를 사용하여 유도하고이 문서의 나머지 부분에 직접 사용하는 것이 (약 25 % 내에서) 서로 충분히 가까이 있습니다. 공개 된 단순화 된 모델 Aε 결과의 수가 증가함에 따라, 이러한 근사치에 대한 필요성이 현저하게 감소한다.

두 보수적 인 가정은 한계 생산 및 붕괴 모드의 더 큰 수의 포함을 허용한다. 첫 번째는 관련된 생산을위한 실험 Aε 적어도 높은 2 개의 생산 모드의 악화 Aε과 같은 것입니다. 에포함 검색, 이것은 일반적으로 좋은 가정이다. 이벤트의 최소 예상 번호는 것

제 합은 모든 생산 모드를 통해 실행되며, 만 B는 단순화 된 모델에서 정확히 어디에 해당 입자는 수학 식 (1)에 포함되는 위치. 마찬가지로, 다른 다리 붕괴에 대한 Aε는 두 다리의 악화 Aε 적어도 높은 것으로 가정 할 수있다. 즉,

양쪽에 서로 다른 붕괴와 다이어그램은 이제 포함 된 곳.

두 개의 추가 가정 STR의 설정을 허용 할 것icter 제한. 하나는 이론에서 모든 생산 모드에 대한 실험 Aε 간략화 모델에 의해 덮여 생산 모드에 대한 평균 Aε 유사하다는 것을 가정 할 수있다. 그 경우, 이벤트의 예상 개수 대신으로 쓸 수있다

금액은 단순화 된 모델에 의해 보호 만 생산 모드에 모두있는 곳. 하나는 더 이상 이론의 모든 붕괴 모드에 대한 Aε이 단순화 된 모델 토폴로지에 포함 해당 이벤트에 대한 평균 Aε 유사하다는 것을 가정 할 수 있습니다. : 다음 이벤트의 예상 수는 다음과 같이 쓸 수있다

여기서 AGA단지 단순화 된 모델을 통해 실행 합합니다. 분명히, 가장 적극적인 MSUGRA 한계는 이러한 가정하에 제공되고, 이와 같이 설정된 한계는, 사실, 전용 검색하여 95 % 신뢰 수준에서 배제되지 않을 영역에 대한 제외 위험을 주장한다. 이 두 근사값의 정확도가 의심이 될 수도 있지만 단순화 된 모델의 포괄적 인 이벤트 운동학 완전한 SUSY 매개 변수 공간 지점에 호의적으로 비교하면, 그들은 불합리하지 않을 수 있습니다.

† 현재 LHC에서 사용되는 몇 가지 단순화 된 모델은 관련 생산 (가) 있습니다. 여기에 명시 적으로 언급되지는 않았지만, 방정식 하찮게이 경우를 허용하도록 확장 될 수있다.

1. 모델 해체

1. NPM의 파라미터 공간에서 플레인을 덮는 양성자 양성자 충돌 이벤트를 생성. 파톤 샤워 hadronization 모델을 포함하는 모든 이벤트 발생 구성을 사용할 수 있습니다. 예 MSUGRA의 경우, 질량 스펙트럼 Isasugra ^33을 사용하여 생성되며, 분기 분획 및 감쇠 폭은 MSSMCalc ^34을 사용하여 계산된다. 그것은 작은 질량 패기 시나리오를 위해 중요 할 수있는 행렬 요소의 추가 방사선을 포함하기 때문에 이벤트 생성 자체, CTEQ 6L1 파튼 밀도 함수 ^(35)와 MadGraph 5 1.3.9 ^(34)은 매트릭스 - 요소 이벤트를 생성하는 데 사용된다. MSUGRA 이벤트를 생성 할 때 MSUGRA을위한 최고의 차 발전기의 LHC 실험 '의 선택을 모방하기 위해, MadGraph 행렬 요소의 추가 복사는 불가능합니다. Pythia 6.425 ^(36)는 다음 SUSY 입자 (sparticle) 붕괴, 파톤 샤워에 사용되는및 hadronization. 이러한 프로그램에 대한 광범위한 문서를 웹에서 쉽게 사용할 수 있습니다.
2. , LHC 검출기 모방 LHC 검출기 매개 카드 PGS 통해 이벤트를 통과하기 위하여. ATLAS와 CMS 검출기 카드 MadGraph 5 ^34에 포함 된 검색 범위 분석을 충분히 수행 할 수 있습니다. 가능한 경우, 식별 및 성능 실험 '매개 변수화가 사용할 수있는 몇 가지 분석과 함께 공개했다. 이상적으로, 이들 실험은 직접적으로 사용될 수 있으며,이 단계는 불필요하다이 경우 단순화 된 모델 격자의 수를 수용하고 효율의 전체 맵을 제공 할 것이다.
3. 신속하게 결과를 분석하기 위해, 중간 경량 데이터 형식이 바람직하다. 제트, 안정 렙톤, 누락 가로 에너지, 편리한 형식 (ExRootAnalysis ^34을 사용하여 예를 들면) PGS 출력에서 기타 필요한 최종 상태의 객체를 추출하는 것이 좋습니다.
4. 주문 t에서O, 결과를 분류 sparticle 제작하여 각 이벤트 감쇠 모드를 분류 할 필요가 발생기 이벤트 레코드의 부분과 PGS 이벤트 결과를 상관. 해당 분기의 분율을 계산하려면 모든 입자 질량, 제작 메커니즘 및 붕괴 체인뿐만 아니라 각각 카운트의 트랙을 유지한다.
5. 그 모델에 가장 적합한 생산 단면 계산을 계산합니다. MSUGRA의 경우, 다음을 선도하는 각 포인트에 대한 주문 단면은 CTEQ 6.6 NLO의 PDF를 사용하여 NLL-FAST ^(38)와 Prospino 2.1 ^37를 사용하여 계산 될 수있다.

2. 모델 재구성

1. NPM의 오픈 생산 및 붕괴 모드의 적어도 50 %를 덮도록 모델 해체에서 고장을 바탕으로 단순화 모델의 사전을 선택한다. 때문에 질량 수용 전형적 두 배 대부분의 BSM 모델의 꾸준함 단면캘리 이론 및 실험 불확실성 내에이 충분히 가까운 만드는 제한 만 20 ~ 50 GeV의를 나타냅니다. off-shell/three-body 붕괴를 포함한 대부분의 직접 부패와 한 단계 붕괴 모델은, LHC 실험으로 간주되었다. CMS는 하나의 종이 ^(21)의 단순화 된 모델 제외 결과의 번호를 수집하고 있습니다. ATLAS와 CMS 모두는 무거운 맛을 단순화하는 다수의 모델로 간주했다. 모델의 전체 목록은 하나의 장소에서 일반에 공개되지 않았습니다. 그러나, 결과는 두 실험의 공개 웹 페이지 ^{39, 40에서} 사용할 수 있습니다. 이들은 NPM의 재건에서 선택해야합니다 단순화 된 모델입니다.
2. 그 시점을 재현하는 데 사용되는 단순화 된 모델로 인한 사람들과 몇 가지 대표적인 NPM 점의 운동학을 비교, 단순화 된 모델 범위의 품질을 테스트하기 위해. 관련 NPM 포인트,와 관련된 단순화 된 모델을 구축적절한 대중.
3. 그 모델로 표현되는 부패에 대한 그 단순화 된 모델의 배 분기 분수로 표시되는 생산 비율을 포함 각 모델 유형에 가중치를 할당합니다.
4. 관련 제조를 위해, 단지 한 쌍의 생산이 지연 모델이 고려되는 경우, 두 개의 중요한 단순화 모델 간의 무게를 나눈다.
5. 그것은 그룹과 유사한 생산 및 붕괴 - 모드에 위해 NPM 이벤트 토폴로지에 물리적으로 동기 부여를 단순화의 집합을 적용하는 것이 좋습니다.
6. 화합 모든 간략화 모델에 대한 가중치의 합을 정상화.
7. 이전의 프로토콜에서 설명한 이벤트 생성 절차를 사용하여 대표 NPM 지점의기구 학적 분포를 계산한다.
8. 전형적인 신호 선택 이후 NPM 포인트의 운동학이 결합한 단순화 모델들 (30 %) σ 이상으로 다르​​다면, 생산 및 감퇴를 향상시키기 위해 부가적인 단순화 된 모델을 포함위상 공간의 범위. 15 % 수준에 차이가 있기 때문에 대부분의 새로운 물리 모델에 빠르게 떨어지는 단면의 최종 배제 결과에 무시할 영향을 미친다.

3. 건축 제한

1. 가능한 및 관련 Aε 및 적용 할 수있는 각각의 실험 신호 지역에서 고려되는 단순화 된 모델에 대한 새로운 물리학 이벤트의 수에 대한 95 % 신뢰 수준 상한을 얻습니다.
2. (있는 경우) 가정 포인트가 제외되고있는 결정하기 위해 각 매개 변수 공간의 점에서 관심의 NPM에 식 (1)과 3-5을 적용합니다.
3. 영역이 제대로 ‡을 결합 할 수 있도록 신호 영역 '배경 불확실성 사이의 상관 관계가 이용 가능하지 않는 한, 최고의 성능을 예상 신호 영역에 의해 설정된 제한을 사용한다.
4. 이전 프로토콜과 배제의 윤곽의 확산으로 수행 운동학의 비교로, RA를 결정NGE하는 실험 배제 거짓말을해야합니다.

‡ 현재, 이러한 상관 관계는 사용할 수 없습니다.

MSUGRA, 출력의 고장의 파라미터 공간에서 포인트 모델 해체 단계를 도포 한 유용한 정보에 따라 생성 된 모든 이벤트에 대한 다양한 생산 및 감쇠 모드를 카운트 업하고 대응하는 생산 속도를 플로팅 및 분수를 분기함으로써 시각화 될 수있다 상대도. 대표적인 MSUGRA 포인트의 다양한 제품 및 붕괴 모드의 분파 분획을도 2 및도 3에 도시되어있다. SUSY 매개 변수 공간에서 다른 점과 비슷한 수치의 상당수는 온라인으로 ^41입니다.

그림 4에서와 같이 MSUGRA의 경우를 들어, 위상 공간에서 몇 가지 경향이 존재한다. Squark 생산은 저 m ₀ 높은 _{m-1 / 2} 영역에 지배하고 gluino 생산 하이 m _0, 저렴한 _{m-1 / 2} 영역에 지배. 지역squark 생산이 지배하는 곳, 직접 squark가 가장 가벼운 초대칭 입자 (LSP)에 붕괴를 선호하고 있습니다. gluino 생산 지배가 그러나 LSP에 gluino 직접 붕괴가 전체 감쇠 위상 공간의 30 % ~ 이상을 포함하지 지역. 개재 지역에서 직접 chargino 생산은 특히 높은 m ₀ squarks 및 gluinos 모든 무거운 높은 m _{1 / 2으로,} 무시할 기여를한다. 이 MSUGRA 평면, 따라서 오 단순화 된 모델 (SM) 시나리오에 의해 커버 될 수있다 :

• 직접 쿼크 (SM 1)의 방출을 통해 LSP에 부패 squarks 쌍의 생산;
• 직접 두 개의 쿼크 (SM 2)의 방출을 통해 LSP에 부패 gluinos 쌍의 생산;
• squarks의 쌍 생산, LSP에 한 단계에있는 부패. squark는 쿼크의 방출을 통해 chargino에 붕괴하고 chargino는 W-보소 (房总)의 방출을 통해 LSP에 붕괴 N (SM 3);
• gluinos의 쌍 생산, LSP에 한 단계에있는 부패. gluino는 두 개의 쿼크의 방출을 통해 chargino에 붕괴하고 chargino는 W-보손 (SM 4)의 방출을 통해 LSP에 붕괴하고,
• 직접 W-보손 (SM 5)의 방출을 통해 LSP에 부패 charginos의 쌍 생산.

이러한 오 단순화 모델 중 하나에 속하는 것으로 분류 MSUGRA 이벤트의 분획은도 5에 도시된다. MSUGRA 예를 들어, 다음과 같은 추가적인 단순화 근사치가 만들어진다 : squark가 gluino에 붕괴되면 gluino 붕괴는 이벤트 토폴로지를 분류에서 계산되고, gluino에 squark의 감퇴를 이벤트에 추가 제트로 계산 ( "플러스 제트")는 초기 또는 최종 상태의 방사선에 동일한 것처럼. gluino는 squark을 통해 자연 붕괴iles/ftp_upload/50419/50419gtilde.jpg 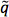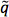"/> → Q , → Q gluino 두 개의 제트를 생성하고 직접 부패했던 것처럼하지만, 붕괴의 최종 상태는 여전히 squark 단계를 생략, 표시, 운동학의 일부 (작은)의 차이를 저장합니다. gluino가없는 중간 squark 쿼크와 한 쌍의 발광 통해 썩은 것처럼 이러한 경우, 따라서 붕괴 체인 (분류 → 전분기 대비 ), 대신에 squark 붕괴로 분류보다추가로 초기 또는 최종 상태의 방사선 조 제트 ( 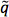→ Q 플러스 제트 (들)). 관련 squark-gluino 생산은 squark 및 gluino 단순화 된 모델에 따라 균등하게 분할된다. 이러한 근사치로, 고려중인 오 단순화 모델의 하나로서 SUSY 이벤트의 많은 부분을 분류하는 것이 가능하다. 이 모델 재구성 향한 첫 단계이다.

이 MSUGRA 파라미터 공간 점 이벤트 운동학은 그것들을 모방하는 데 단순화 모델의 조합과 함께,도 6, 7 및 8에 나타낸다. 이들 두 점은 상기 한 방법을 이용하여 해체하고, 선택한 5 개의 단순화 모델은 질량 스펙트럼, 생산율에 따라 구성 및 조합, 및점 분획 분파. 단순화 된 모델 이벤트는 MSUGRA 이벤트와 동일한 방식으로 생성 및 분석 하였다. 여기에, LHC 초대칭 검색에 사용되는 키 학적 변수의 네 가지가 나와 있습니다 최고의 제트 가로 모멘텀 (P의 _T), 렙톤 P의 _T, 누락 가로 에너지 및 유효 질량을 가로 운동량 네 가지의 주요의 스칼라 합으로 정의 제트기와 렙톤. 두 기능은 제트을 선도하고, 가로 에너지 분포를 누락, 강력한 생산 및 weakino 생산에 해당하는 유효 질량에 볼 수 있습니다. 이러한 포함 배포판에서 일부 차이가 명확하게 볼 수 있습니다. 낮은 P _T의 렙톤의 꼬리는, 예를 들어, 단순화 된 모델의 적용을받지 않습니다 타우 붕괴에서 주로합니다. 낮은 누락 가로 에너지가 낮은 유효 질량 영역은 모델링되지 LSP-X 관련 생산에서 일부입니다. 대부분의 운동 기능이 설명되어 있습니다꾸준함 배경 파라미터 공간에서의 탐색 목적 PGS 의해 충분히. 타우 가짜 요금은 타우 분석 결과의 파라미터에 상당한 도전을 유지하며, 완전하게 그 문제를 해결하는 것은이 프로토콜의 범위를 벗어납니다.

그러나 LHC에서 사용되는 대부분의 신호 영역의 삭감 심플 붕괴 토폴로지가 더 복잡 종종 부드러워 이상 다수의 이벤트에 걸쳐 선택되도록 설정된다. 따라서, 신호 영역의 선택은 단순화 된 모델에 의해 이벤트 운동학의 설명을 개선하는 경향이있다. 최근 ATLAS SUSY 검색 ^16에서 사용 된 것과 유사한 한 렙톤 영역의 비교는도 7 및 8에 나타낸다. 모양과 꼬리 모두 계약은 훨씬 더 나은 것입니다. 단순화 된 모델에 대한 운동학은 완전한 SUSY 포인트에 대한 효율성 및 수용이 잘 설명 될 수 있다는 것을 제안, 포함 SUSY 모델 운동학에 잘 비교단순화 된 모델의 제한된 조합에 의해 수행 될 수있다. 물론, 간단한 모델에 의해 설명 토폴로지에 해당하는 만 SUSY 이벤트의 운동학은 단순화 된 모델의 대응과 동일합니다. 이것은 이러한 단순화 된 모델에 포함되지 않은 사건이 전체 사건이나 적용되는 것과 유사한 운동 학적으로 작은 부분 하나 있다는 것을 확인 역할을합니다. 이 MSUGRA의 경우 모델의 재구성 단계를 완료합니다.

제 3 항에 따라 제한 - 설정 절차는 다음 = 10 황갈색 β와 MSUGRA 평면에 적용되는 A = 0 _0> 0 μ, ATLAS 제로 렙톤 검색 ^16에서 신호 영역을 사용하여.에게 다섯 신호 영역이 검색 결과에 포함되고, 유용한 것으로 제한과 신호 영역은 각 시점을 위해 사용된다. 최적의 신호 영역에서 예상 SUSY 이벤트의 수는 관찰 된 95 % 신뢰 수준을 초과하는 경우는 점 제외 여겨진다그 신호 지역에서 새로운 물리학의 이벤트에 대한 상한. 그림 9에서, 전술 한 바와 같이 단순화 된 모델의 배제의 결과는, 신호에 대한 체계적인 불확실성없이 제로 렙톤 제외 비교된다. 네 단순화 된 모델 제외 곡선은 식 (1)과 3-5에 해당하는 표시됩니다. 제로 렙톤 제외 제한에 비교하여, 가장 보수적 인 단순화 된 모델 기반의 접근 방식은 지배 지역에서 다소 저조한 수행 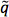및 weakino 생산 관련, ~ 100 GeV의 최대하여 올바른 제한이 없습니다. 이 (그림 3에서 열려있는 형태의 다수의 CF)으로 인해 gluino의 상대적으로 복잡한 붕괴로 부분도있다. 범위는 진정한 한계에 훨씬 더 가깝다지배 지역에 대한 과 생산은하는 단순화 된 모델에서 파생 된 제한은 사실 한계의 40 GeV의 조건을 제공합니다.

이 처방 신호 모델에 이론적 불확실성 처리를 생략. 사실, LHC 실험은 현재 일관성있는 방법으로 이러한 불확실성을 취급하지 않습니다, 또는 불확실성이 모두 포함되어 있습니다. 어떤 실험은, 예를 들어, GUT 규모 매개 변수에서 볼 수 대중의 계산에 불확실성이 포함되어 있지 않습니다. 일의 한계여기 제시에 따라서 발행 한계 다를 것으로 예상한다. 그림 10에서, 제로 렙톤 채널에 게시 된 ATLAS 제외 제한은 신호에 대한 체계적인 불확실성없이 여기에서 얻은 결과와 비교된다. 신호 불확실성이없는 한계가 게시 된 제한보다 명확하게 높다. 용지의 나머지 부분 신호 체계적인 불확실성없이 제한 단순화 모델을 이용하여 도착하는 "정답"로 간주 될 것이다. 이론적 불확실성 같은 방식 모두에 추가 될 수 있으며, 거의 동일한 방법으로 두 한계에 영향을 미칠 것이다.

가능한 한 정확하게 현재의 자원을 결과를 달성 묘사하기 위해 단순화 된 모델의 포인트는 이미 ATLAS 실험 ^17에서 사용하는에 대략 대응하는 그리드에 생성됩니다. 이러한 점 사이 Aε는 두 개의 차원 m에서 보간squark / M _gluino = m _{LSP 격자입니다.} 이 실험은 가득 차있는 3 차원 Aε를 제공 할 가능성이 거의 없으므로 SM 3와 SM 4 세 차원 그리드, 그리고 있기 때문에, 중간 chargino 질량의 세 가지 값이 사용됩니다 : M의 _chargino = X × (M의 _{squark / gluino} - M의 _LSP) + M _LSP, X = 0.25, 0.5, 0.75. 이 세 개의 차원 평면 보간하기 위해, 간단한 차 적합 사용됩니다. m의 _LSP = M의 _chargino 및 m의 _{squark / gluino의} 경계에 접근 할 때, 붕괴 모드는 자연적으로 더 복잡한 보간이 필요하고, 전원을 끄십시오.

제외 곡선을 비교에서, 하나는 참으로 보수적 배제 한계가 식을 사용하여 설정 한 것을 볼 수 있습니다. 1은 단순화 된 형태로 잘 덮여 위상 공간의 지역에서 아주 잘 "올바른"배제 제한을 다음과LS (참조 그림 5). 뿐만 아니라 식, 포함되지 않는 지역에서는. 3은 여전히​​ 보수적 인 한계를 제공합니다. 공격적인 한계는 식으로 설정합니다. 긴 gluino 붕괴 체인이 있다는 가정의 짧은 체인으로 잘 모델링하기 때문에 5, squark 지배하는 지역의 위상 공간의 gluino가 지배하는 지역에서 최대 100 GeV의에 의해 최대 40 GeV의에 의해 배제를 과대 평가 단순화 된 모델은 어떤 수준에서 유효하지 않습니다. 매개 변수 공간 범위, 20 % 언더 커버 보수 제한, 언더 커버 10 % 가운데 두 제한 및 오버 커버 10 % 공격적인 제한의 측면에서. 물론, 사용 가능한 단순화 모델의 사전을 확대하는 보수적 인 한계를 개선하고보다 정확한 Aε 등 공격적인 제한을 줄일 수는 더 많은 생산과 붕괴 모드에 포함되어 있습니다. 그러나, 단순화 된 모델이 소수의 보수적 한계 세트는 "수정"결과에 가깝다.

실증을 위해, 한계도 높은 황갈색 β에 MSUGRA 신호 영역에 배치됩니다. 제한 사항은 그림 11에 표시됩니다. 도 10에서 관찰 계약에 기초하여, 실험 배제 비트 식에 의해 설정된 제외 넘어 거짓말한다. 3.

더 이국적인 이론을 외삽에, 또는 이론을 SUSY 단순화 된 모델의 작은 목록의 적용 확대에, 여러 가지 가정을 할 수있다 :

1. 즉, 무거운 맛 제트는 맛이 태그를 포함하지 않고 검색을위한 가벼운 맛 제트 동일합니다;
2. 광자는 광자를 식별하지 않는 검색을위한 제트기 동일한 지;
3. 즉, 절반 이상 시간, chargino (neutralino는) gluino 기능적으로 동일 서명이 두 개의 쿼크의 방출을 통해 붕괴 생산 W-보손 (Z-보손)의 방출을 통해 LSP에 붕괴.

그림 1. 왼쪽, ATLAS 세 제트 "느슨한"한 렙톤 신호 영역 ^(17)에 대한 공개 Aε. 마우스 오른쪽 단추로, 여기에 사용 MadGraph + Pythia + PGS 설정에서 재생 동일. 약간의 차이는 여기에 사용 된 다른 발전기와 높은 통계를 예상 할 수 있지만, 두 사람은 서로 밀접하게 따릅니다. 큰 그림을 보려면 여기를 클릭하십시오 .

19/50419fig2highres.jpg "SRC ="/ files/ftp_upload/50419/50419fig2.jpg "/>
그림 2. SUSY 생산 메커니즘과 MSUGRA 매개 변수 공간에서 붕괴 모드에 대한 비율을 분기. 맨 윗줄 (m ₀ = 300 GeV의, m _{1 / 2} = 600 GeV의, 황갈색 (β) = 10, ₀ = 0 GeV의, 및> 0 μ )는 squark 생산에 의해 지배된다 매개 변수 공간에서 지역의 전형적인, 그리고 맨 아래 행 (m ₀ = 1000 GeV의, m _{1 / 2} = 350 GeV의, 황갈색 (β) = 10, ₀ = 0 GeV의 한 μ > 0)이 두 극단 사이에 다소 누워 매개 변수 공간에서 지역의 전형이다. 그들의 분기 분획 0.5 %보다 크면 명확화를 위해, 생산 및 감쇠 모드 만 나열된다. 번호와 레이블 "SM은"모델 재구성 프로토콜에서 논의 된 단순화 된 모델에 해당 붕괴 모드로 제공됩니다.les/ftp_upload/50419/50419fig3large.jpg "대상 ="_blank "> 큰 그림을 보려면 여기를 클릭하십시오.

그림 3. SUSY 생산 메커니즘과 MSUGRA 매개 변수 공간에서 붕괴 모드에 대한 비율을 분기. 맨 윗줄 (m ₀ = 300 GeV의, m _{1 / 2} = 500 GeV의, 황갈색 (β) = 25, ₀ = 1,500 GeV의, 그리고 μ> 0) squark 생산에 의해 지배되는 매개 변수 공간에서 지역의 전형적인, 그리고 맨 아래 행 (m ₀ = 2,100 GeV의, m _{1 / 2} = 100 GeV의, 황갈색 (β) = 45, ₀ = 500 GeV의 그리고 μ> 0) gluino 생산에 의해 지배 지역에 대한 일반적입니다. 이해를 돕기 위해, 생산 및 붕괴 모드 만 표시되는 경우그들의 분파 분획 0.5 %보다 크다. 번호와 레이블 "SM은"모델 재구성 프로토콜에서 논의 된 단순화 된 모델에 해당 붕괴 모드로 제공됩니다. 흰색 영역에서 모델이 제한 몬테카를로 통계로 단순화 모델에 의해 설명에 이벤트를했다. 큰 그림을 보려면 여기를 클릭하십시오 .

그림 4. 탄 (β)와 MSUGRA 매개 변수 공간에서 주요 SUSY 생산과 붕괴 모드의 퍼센트 분기 비율의 변화는 10, _0과 μ> = 0. 강한 sparticles은 오른쪽 상단에, 무거운, 중요한 CONTR을 포함 weakino 생산에서 ibution. 흰색 영역에서 모델이 제한 몬테카를로 통계로 단순화 모델에 의해 설명에 이벤트를했다. 큰 그림을 보려면 여기를 클릭하십시오 .

그림 5. 낮은 황갈색 (β)의 경우, 본 논문에서 고려 다섯 단순화 된 모델 중 하나에 속하는 것으로 분류 MSUGRA 이벤트의 비율 (왼쪽)와 고 황갈색 (β) (오른쪽). 큰 그림을 보려면 여기를 클릭하십시오 .

419fig6highres.jpg "SRC ="/ files/ftp_upload/50419/50419fig6.jpg "/>
그림 6. squark 생산 지배 MSUGRA 포인트 (m ₀ = 300 GeV의, m _{1 / 2} = 600 GeV의, 황갈색 (β) = 10, ₀ = 0 GeV의, 그리고 μ> 0)과 세트의 운동학 다섯 단순화 된 모델은 왼쪽에서 같은 질량 스펙트럼. 시계 방향을 사용하여 제트 P의 _T를 선도, 뮤온 P의 _T, 유효 질량을 선도하고, 가로 에너지를 누락 건설. 신호 선택 적용되었습니다. 큰 그림을 보려면 여기를 클릭하십시오 .

그림 7. squark-produ의 운동학ction의 지배 MSUGRA 포인트 (m ₀ = 300 GeV의, m _{1 / 2} = 600 GeV의, 황갈색 (β) = 10, ₀ = 0 GeV의, 및> 0 μ) 다섯 단순화 된 모델 세트는 같은 질량을 사용하여 구성 스펙트럼. 시계 방향으로 왼쪽, 최고의 제트 P의 _T, 선도적 인 뮤온 P의 _T, 유효 질량, 누락 가로 에너지에서. 한 렙톤 네 제트 "꽉"ATLAS SUSY 검색과 유사한 신호 선택이 적용되었습니다. 큰 그림을 보려면 여기를 클릭하십시오 .

그림 8. 복잡한 MSUGRA 점의 운동학 (M ₀ = 1000 GeV의, m _{1 / 2} =350 GeV의, 황갈색 (β)는 10, ₀ = 0 GeV의를 = 및 μ> 0) 다섯 단순화 된 모델의 집합, 왼쪽에서 같은 질량 스펙트럼. 시계 방향을 사용하여 제트 P의 _T를 선도, 뮤온 P의 _T를 선도하는 건설 , 유효 질량, 그리고 누락 된 가로 에너지. 한 렙톤 네 제트 "꽉"ATLAS SUSY 검색과 유사한 신호 선택이 적용되었습니다. 큰 그림을 보려면 여기를 클릭하십시오 .

그림 9. 배제 한계와 비교 = 10 황갈색 β, ₀ = 0, μ> 0 (10A)와 MSUGRA 모델 제로 렙톤 제외 제한을 결합단순화 된 모델을 이용하여 얻어진 단 (10B). 유용한 것으로 제한을 제공하는 신호 영역은 파라미터 공간에서 주어진 지점에 대해 수행된다. 예상되는 95 % 신뢰 수준 제한은 파란색 파선으로 표시되고, 관찰 제한은 빨강 색 선으로 표시됩니다. 이러한 제한 중 일부는 약간 다른 매개 변수의 선택을 사용하여 제작되었다하더라도 이전 검색의 결과는 또한, 비교를 위해 ^{42 ~ 48에} 표시됩니다. 단순화 된 모델의 한계는 본문의 한계 방정식에 해당하는 가정의 네 가지 세트를 사용하여 생성됩니다. 큰 그림을 보려면 여기를 클릭하십시오 .

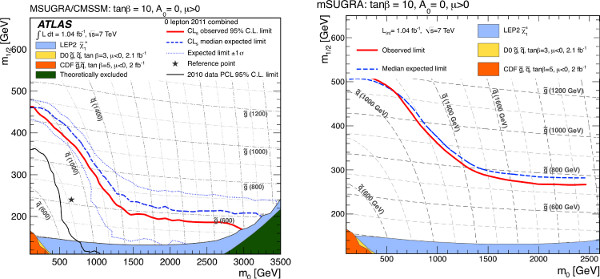
그림 10. 에 대한 결합 제로 렙톤 제외 제한= 10 황갈색 β, PGS를 사용하여 얻은 배제 한계로 및 신호에 대한 체계적인 불확실성없이 비교 (왼쪽) ₀ = 0, μ> 0 ¹⁶ MSUGRA 모델. 신호 영역이 가장 기대되는 한도를 제공하는이를 위해 촬영 매개 변수 공간에 포인트가 없습니다. 예상되는 95 % 신뢰 수준 제한은 파란색 파선으로 표시되고, 관찰 제한은 빨강 색 선으로 표시됩니다. 이러한 제한 중 일부는 약간 다른 매개 변수의 선택을 사용하여 제작되었다하더라도 이전 검색의 결과는 또한, 비교를 위해 ^{42 ~ 48에} 표시됩니다. 큰 그림을 보려면 여기를 클릭하십시오 .

인터넷gure 11. = 40 황갈색 β와 MSUGRA 모델 제외 제한, ₀ = -500 GeV의와 μ> 0 (왼쪽)과 황갈색 = 20 β, ₀ = 500 GeV의와> 0 μ가 (오른쪽) 단순화 된 모델을 이용하여 얻어진 만 . 결합 한계는 파라미터 공간에서 각 점에 유용한 것으로 한계가 발생하는 신호 영역을 사용하여 획득된다. 단순화 된 모델의 한계는 본문의 한계 방정식에 해당하는 가정의 네 가지 세트를 사용하여 생성됩니다. 큰 그림을 보려면 여기를 클릭하십시오 .

완전히 새로운 물리 모델에서 제외 형상을 생성하는 단순화 된 모델 제한 애플리케이션은 입증되었다. MSUGRA 파라미터 공간 포인트 명백한 복잡성에도 불구하고, 운동학 간략화 모델의 단지 적은 수의 조합에 의해 잘 재생할 수있다. 특정 신호 영역 내에서 볼 때 지금까지 LHC에서 실시 검색 높은 P의 _{T 개체의} (상대적으로) 적은 수의 단순화 된 모델과 같은 이벤트 토폴로지를 선호하는 경향이 있기 때문에 운동 학적 계약은 더욱 향상됩니다.

단순화 된 모델에서 파생 제외 윤곽은 이미 전용 검색에 게시 된 사람들과 비교해도 손색. 이 절차로, 평범 이국적인 SUSY 이론, 또는 단순화 된 모델에 포함 서명 nonSUSY 이론에에 제외 결과를 재조명 할 수 있습니다. 이 방법은 또한 데이터의 보존을위한 간단한 경로를 허용차 미래 이론 현재의 검색 응용 프로그램입니다.

실제적으로,이 방법은 LHC 실험 LHC 이론가 현상 학자에 큰 이익을 위해 절약 중요한 자원을 의미한다. 정보 행렬 요소 및 붕괴 가능성에서 사용할 수를 사용하여 이론을 개주으로, 모델의 어떤 컴퓨팅 집약적 인 시뮬레이션이 수행되어야합니다. 하지만 완전히받을 수 없습니다 - - 간단한 최종 상태의 서명 대신, 실험은 똑 바르게 포함 이론적 모델의 큰 다양성에서 제외 결과를 제공하기 위해 무료입니다. 마찬가지로, 이론가들은 LHC 실험들이 선호하는 모델의 한계를 생산하기 위해 기다릴 필요가 없습니다. 단순화 된 모델은 단순화 모델의 상대적으로 적은 수의 모델의 모든 생산 및 감쇠 모드를 커버하지 않을 수도 있지만 이는 가능성의 매우 넓은 범위를 커버 할 수있다. 이러한 방식으로 취득한 제외 정확하게 완전한 실험의 결과를 겹치지정신 검색. 현재 LHC 검색 시대에, 그러나, 그들은 이론 공간이 이미 이미 실시 검색에서 제외되어 얼마나 중요하고 놀라 울 정도로 정확한 추정을주고, 얼마나 많은 여전히​​ 검색에 노출 될 수 있습니다.

저자는 두 ATLAS 공동의 구성원입니다. 그러나, 그렇지 않으면 더 ATLAS 내부 금전적 자원, 또는,이 작품의 완성에 사용되지 않았다.

저자는 단순화 된 모델과 잠재적 인 함정의 중요한 논의 제이 바커에게 감사의 말씀을 전합니다. 건설적인 비판과 격려가 필요하다고 할 때마다에 대해서도 최대 Baak 및 Eifert 틸 많은 감사. 이 협력이 가능하게하기위한 CERN 여름 학생 프로그램에 감사합니다.