Définition des limites sur la supersymétrie l'aide de modèles simplifiés

Cet article démontre un protocole de refonte des limites des modèles simplifiés expérimentales dans des limites conservatrices et agressifs sur un nouveau modèle de la physique arbitraire. Publiquement disponibles LHC résultats expérimentaux peuvent procéder à une refonte de cette manière dans les limites sur presque n'importe quel nouveau modèle de la physique avec une signature de la supersymétrie-comme.

Limites expérimentales sur la supersymétrie et les théories similaires sont difficiles à définir en raison de l'énorme espace disponible sur le paramètre et difficile de généraliser en raison de la complexité de ces guichets uniques. Par conséquent, plus phénoménologiques, des modèles simplifiés sont de plus populaire pour fixer les limites expérimentales, car ils ont des interprétations physiques claires. L'utilisation de ces limites de modèles simplifiés de fixer une limite réelle sur une théorie concrète n'a cependant pas été démontrée. Ce document est une refonte des limites des modèles simplifiés dans des limites sur un modèle de la supersymétrie spécifique et complète, la supergravité minimale. Limites obtenues sous diverses hypothèses physiques sont comparables à celles produites par les recherches dirigées. Une ordonnance a été faite pour le calcul des limites conservatrices et agressifs sur les théories supplémentaires. Utilisation des tableaux d'acceptation et d'efficacité ainsi que les numéros attendus et observés de manifestations dans différentes régions de signaux, les résultats expérimentaux LHC peuvent être refondus dans cette machinenner dans presque n'importe quel cadre théorique, y compris les théories nonsupersymmetric avec des signatures de supersymétrie-comme.

L'une des extensions les plus prometteurs du modèle standard, la supersymétrie (SUSY) ^1-14, est le point central de nombreuses recherches par les expériences du LHC au CERN. Les données recueillies en 2011 sont déjà suffisantes pour repousser les limites de la nouvelle physique au-delà de ceux de toute collisionneur précédente ^15-22. Que de nouvelles données arrivent et des exclusions sont poussés encore plus loin, il sera de plus en plus important de communiquer clairement à la communauté de la physique ce que les régions de l'espace étendu de paramètres supersymétrique ont été exclus. Les limites actuelles sont généralement fixés sur des plans en deux dimensions limitées, qui ne représentent souvent pas la diversité disponible espace des paramètres SUSY et sont difficiles à comprendre que les limites sur les masses physiques ou fractions de branchement. Un grand nombre de modèles simplifiés ^{23, 24} ont été proposés pour aider à la compréhension de ces limites, et les deux ATLAS et CMS ont fourni des résultats d'exclusion pour plusieurs de ces modèles ^15-20.

Cet article démontre l'application de ces exclusions de modèle simplifié à un modèle de la physique nouvelle complète en utilisant l'exemple de la supergravité minimale (mSUGRA, également connu sous le CMSSM) ^25-30. Ce modèle est choisi afin de comparer les limites fixées à l'aide de modèles simplifiés à celles publiées indépendamment par les expériences. La procédure est suffisamment général pour pouvoir être accordé à tout nouveau modèle de la physique (NPM). En ce qui représente la première tentative de «boucler la boucle» et fixer des limites sur SUSY utilisant des modèles simplifiés, un certain nombre d'hypothèses quant à l'applicabilité de limites sur certains modèles simplifiés sont explorées, résultant dans des recettes de l'établissement de limites conservatrices et agressifs sur les théories qui ont pas été examinée par les expériences du LHC.

Pour fixer une limite dans un mécanisme national de prévention, trois opérations distinctes sont nécessaires. Tout d'abord, le MNP doit être décomposé en ses éléments constitutifs, en séparant les différents producteursmodes ction et modes de désintégration de tous les nouveaux particules dans le modèle. Deuxièmement, un ensemble de modèles simplifiés doit être choisi de recréer la cinématique et les topologies d'événements pertinents dans le MNP. Troisièmement, les limites disponibles sur ces modèles simplifiés doivent être combinés afin de produire des limites sur la NGP. Ces trois procédures sont décrites dans le protocole. Quelques approximations supplémentaires sont également fournis qui peuvent élargir l'applicabilité des modèles simplifiés déjà disponibles à un plus large éventail de topologies d'événements.

Un mécanisme national de prévention complète implique généralement de nombreux modes de production et de nombreuses caries ultérieures possibles. La déconstruction de nouveaux modèles de physique dans leurs composants et l'application des limites des modèles simplifiés de ces composants permet la construction d'une exclusion limiter directement. Pour n'importe quelle région de signal, la limite la plus conservatrice peut être réglée en utilisant la fraction de production P _{(a, b)} (où a, b représente le modèle simplifié spamode de production Article) des événements identiques à un modèle simplifié i et la fraction de branchement pour les sparticules produites à la désintégration de la manière décrite par le modèle † simplifiée, BR _{a → i} x BR _{b → i.} Le nombre d'événements attendu dans une région donnée du signal de ces topologies simples peut alors s'écrire

où la somme porte sur des modèles simplifiés, σ _tot est la section totale pour le point NPM, L _int est la luminosité intégrée utilisée dans la recherche, et AE _{a, b → i} est l'acceptation fois l'efficacité pour les événements du modèle simplifié de la région du signal considéré. Ce nombre peut être comparé à la limite supérieure de niveau de confiance de 95% attendue sur le nombre de nouveaux événements de physique to sélectionner la zone de recherche optimale. Le modèle peut alors être exclue si N est plus grand que le nombre observé de nouveaux événements de la physique exclus au niveau de confiance de 95%. Exclusions dans les régions ne se chevauchent peuvent être combinés si les informations sur les corrélations de leurs incertitudes est disponible. Si cette information n'est pas disponible, la meilleure région de signal ou d'analyse qui fournit la meilleure limite attendue peuvent être utilisées pour tenter d'éliminer le modèle.

Afin de construire des limites concrètes de cette méthode, la Aε pour divers modèles simplifiés doit être mis à disposition par les expériences du LHC. La CMS et ATLAS ont publié des chiffres avec le Aε pour plusieurs modèles, et quelques-uns des chiffres sont disponibles dans la base de données HepData ^31. Afin de démontrer la valeur de la publication de toutes ces tables, nous pensons qu'il est important de prévoir des limites concrètes qui sont comparables à ceux déjà publiés. Par conséquent, nous utilisons (et décrivante dans le protocole comme une étape facultative) une simulation de détecteur rapide d'imiter l'effet de l'ATLAS ou détecteur CMS. Le dérivé de la Aε Pretty Good simulation (ES) ³² est comparée à celle publiée par ATLAS à une grille du modèle simplifié de la figure 1. Ces résultats sont suffisamment proches l'un de l'autre (dans environ 25%) qui, plutôt que d'attendre tous les résultats soient publiques, les résultats Aε pour les grilles restantes sont calculés à l'aide PGS et utilisés directement dans la suite de cet article. Comme le nombre de places publiquement modèle simplifié résultats Aε se développe, la nécessité de ces approximations doit être réduite de manière significative.

Deux hypothèses prudentes permettent l'inclusion d'un plus grand nombre de production et de désintégration des modes dans la limite. Le premier est que, pour la production associée Aε expérimental est au moins aussi élevée que la Aε pour le pire des deux modes de production. Pourrecherches inclusives, c'est généralement une bonne hypothèse. Le nombre d'événements minimum prévu serait alors

où la première somme porte sur tous les modes de production, et seulement ceux où a et b sont exactement les particules du modèle simplifié sont inclus dans l'équation 1. De même, la Aε pour désintégrations avec différentes jambes peut être considérée comme étant au moins aussi élevée que la Aε pour le pire des deux jambes. Autrement dit,

où diagrammes avec différentes désintégrations de chaque côté ont été inclus.

Deux autres hypothèses pourraient permettre la création de strlimites de ictère. On peut supposer que la Aε expérimental pour tous les modes de la théorie de production est similaire à la Aε moyenne pour les modes de production couverts par des modèles simplifiés. Dans ce cas, le nombre attendu d'événements peut être écrite comme la place

où les sommes sont à la fois plus que les modes de production couverts par des modèles simplifiés. On peut en outre supposer que la Aε pour tous les modes de désintégration dans la théorie est similaire à la moyenne Aε pour les événements couverts par les topologies de modèles simplifiés. Ensuite, le nombre d'événements attendu peut être écrite comme:

où agadans les sommes gérées uniquement sur les modèles simplifiés. De toute évidence, la limite la plus agressive mSUGRA est prévu dans cette hypothèse, et une limite fixée de cette manière risque de réclamer l'exclusion pour les régions qui ne seraient pas, en fait, être exclus au niveau de confiance de 95% par une recherche spécifique. Bien que la précision de ces deux approximations pourrait être suspect, si la cinématique d'événements compris des modèles simplifiés se comparent favorablement à un point de l'espace des paramètres SUSY complète, ils peuvent ne pas être déraisonnable.

† Certains modèles simplifiés utilisés aujourd'hui au LHC comprennent la production associée. Bien que n'étant pas explicitement discuté ici, les équations peuvent être trivialement étendu pour permettre ce cas.

Une. Modèle déconstruction

1. Générer des événements de collision proton-proton couvrant un plan dans l'espace des paramètres du MNP. Toute configuration de générateur d'événements qui comprend une douche de parton et modèle de hadronisation peut être utilisé. Dans le cas de mSUGRA par exemple, les spectres de masse sont générés en utilisant Isasugra ^33, et les fractions de ramification et des largeurs de désintégration sont calculés en utilisant MSSMCalc ^34. Pour la génération de l'événement lui-même, MadGraph 5 1.3.9 ³⁴ avec CTEQ 6L1 fonctions de densité de parton ³⁵ est utilisé pour générer des événements matrice-élément, car il comprend un rayonnement supplémentaire dans l'élément de matrice, qui peut être important pour les petits scénarios masse de fractionnement. Pour imiter les choix des expériences LHC de générateurs leader ordre pour mSUGRA, le rayonnement supplémentaire dans l'élément de matrice de MadGraph est désactivé lors de la génération des événements mSUGRA. Pythie 6,425 ³⁶ est ensuite utilisé pour SUSY particules (sparticule) décroissance, parton douche,et hadronisation. Une large documentation pour l'un de ces programmes est facilement disponible sur le web.
2. Pour imiter un détecteur du LHC, passer les événements par PGS avec une carte de paramètre LHC-détecteur. Les cartes de détecteurs ATLAS et CMS inclus avec MadGraph 5 ³⁴ effectuer assez bien pour l'analyse de recherche de portée. Le cas échéant, les paramétrages d'identification et de performance des expériences rendues publiques par certaines analyses peuvent être utilisés. Idéalement, les expériences fourniront cartes complètes de l'acceptation et de l'efficacité pour un certain nombre de grilles de modèle simplifié, auquel cas ceux-ci peuvent être utilisés directement et cette étape est inutile.
3. Afin d'analyser rapidement les résultats, un format de données léger intermédiaire est souhaitable. Extraire les jets, les leptons stables, énergie manquante transverse, et d'autres objets de l'Etat-finale nécessaires à partir de la sortie PGS (par exemple en utilisant ExRootAnalysis ³⁴⁾ dans un format pratique est recommandée.
4. Pour to classer les résultats, une corrélation entre les résultats des épreuves PGS avec la partie de l'enregistrement de l'événement générateur nécessaire de classer la production de sparticule et modes de désintégration pour chaque événement. Garder la trace de toutes les masses de particules, les mécanismes de production et les chaînes de désintégration ainsi que leurs chiffres respectifs afin d'être en mesure de calculer leur fraction de ramification correspondant.
5. Calculer les meilleurs disponibles production calculs de section pour le modèle d'intérêt. Dans le cas de mSUGRA, avant-premier ordre des sections pour chaque point peut être calculée en utilisant Prospino 2.1 ³⁷ avec NLL-Fast ³⁸ en utilisant CTEQ 6.6 PDF NLO.

2. Modèle reconstruction

1. Sur la base de la répartition de la déconstruction modèle, choisir un dictionnaire de modèles simplifiés de manière à couvrir au moins 50% des modes de production et de la NGP désintégration ouvertes. En raison de la coupe chute rapide de la plupart des modèles de BSM avec la masse, un facteur de deux dans l'acceptation Typiment ne représente que 20-50 GeV à la limite, ce qui en fait suffisamment proche pour être dans les incertitudes expérimentales et théoriques. La plupart décroissance directe et modèles de désintégration en une seule étape, y compris les désintégrations off-shell/three-body, ont été considérés par les expériences du LHC. CMS a recueilli un certain nombre de résultats d'exclusion de modèle simplifié en un seul document ^21. Les deux ATLAS et CMS ont également examiné un certain nombre de gros-goût des modèles simplifiés. La liste complète des modèles n'a pas été rendu public en un seul endroit. Cependant, les résultats sont disponibles à partir de pages Web publics des deux expériences ^{39, 40.} Ce sont les modèles simplifiés qui doivent être choisis parmi la reconstruction du MNP.
2. Afin de tester la qualité de la couverture de modèle simplifié, comparer la cinématique de quelques points de la NGP représentatives de celles résultant des modèles simplifiés utilisés pour reproduire ce point. Pour un point de NPM donné, construire des modèles simplifiés pertinents avec lemasses appropriées.
3. Attribuer un poids à chaque type de modèle qui inclut la fraction de la production représentée par ce temps de modèle de la fraction simplifiée de branchement pour la décroissance représentée par ce modèle.
4. Pour la production associée, si seulement deux-production des modèles simplifiés sont considérés, diviser le poids entre les deux modèles simplifiés appropriés.
5. Il est recommandé d'appliquer un ensemble de simplifications physiquement motivés pour les topologies d'événements MNP afin de regrouper la production et la pourriture modes similaires.
6. Normaliser la somme des poids pour tous les modèles simplifiés à l'unité.
7. Calculer les distributions cinématiques pour les points représentatifs de la NGP en utilisant la procédure de génération d'événements décrit dans le protocole précédent.
8. Si la cinématique du point de NPM sélections de signaux typiques diffèrent de plus de σ (30%) de ceux des modèles simplifiés combinés, y compris des modèles simplifiés supplémentaires pour améliorer la production et la désintégrationcouverture l'espace des phases. Les divergences sur le niveau de 15% ont un impact négligeable sur les résultats finaux d'exclusion en raison de la baisse rapide des sections dans la plupart des nouveaux modèles de la physique.

3. Limiter la construction

1. Obtenir le Aε disponibles et pertinentes et à 95% la limite supérieure de niveau de confiance sur le nombre de nouveaux événements de physique pour les modèles simplifiés envisagées dans chaque région de signal expérimental qui peut être appliquée.
2. Appliquer les équations 1 et 3-5 pour la NPM d'intérêt à chaque point de l'espace des paramètres à déterminer en vertu de laquelle (le cas échéant) des hypothèses point est exclue.
3. Utilisez la limite fixée par la région de signal avec la meilleure performance attendue, à moins que les corrélations entre les incertitudes fond des régions de signaux sont disponibles afin que les régions puissent être correctement combinés ‡.
4. Avec la comparaison de la cinématique réalisée avec le protocole précédent et la propagation des contours d'exclusion, de déterminer la raESN dans lequel l'exclusion expérimental devrait se situer.

‡ À l'heure actuelle, aucune de ces corrélations sont disponibles.

Après avoir appliqué la déconstruction étape de modèle à un point dans l'espace des paramètres de mSUGRA, une répartition de la production peut être mieux visualisé en comptant les différents modes pour chaque événement généré production et de décroissance et tracer les taux de production correspondants et la ramification des fractions selon l' les fréquences relatives. Les fractions de ramification pour les différents modes de représentation pour des points mSUGRA production et de désintégration sont illustrés sur les figures 2 et 3. Un grand nombre de chiffres similaires pour d'autres points dans l'espace des paramètres SUSY sont disponibles en ligne ^41.

Pour le cas de mSUGRA, certaines tendances à travers l'espace de phase sont présents, comme le montre la figure 4. Production Squark domine dans le bas-m _0, haute m _1/2 région, et la production de gluino domine dans la haute m _0, bas-m _1/2 région. Dans la régionoù la production de squark domine, squark directe se désintègre à la particule supersymétrique la plus légère (LSP) sont favorisés. Dans les régions où domine de production de gluino cependant désintégrations directes de la gluino sur le LSP ne comprennent plus d'environ 30% de l'espace de phase de chute totale. Dans la région intercalée, la production de chargino directe constitue une contribution non négligeable, en particulier vers la haute m ₀ et m de haut _1/2 où les squarks et gluinos sont tous lourds. Ce plan mSUGRA, donc, peut être couvert par cinq modèles (SM) des scénarios simplifiés:

• Paire-production de squarks, qui se désintègre directement sur le LSP via l'émission d'un fromage blanc (SM 1);
• Pair-production de gluinos, qui se dégrade directement au LSP via l'émission d'un deux quarks (SM 2);
• Pair-production de squarks, qui se désintègrent en une seule étape pour le LSP. Le squark se désintègre en un chargino via l'émission d'un fromage blanc, et la chargino se désintègre à la LSP par l'intermédiaire d'une émission de W-boso n (SM 3);
• Pair-production de gluinos, qui se désintègrent en une seule étape pour le LSP. Le gluino se désintègre en un chargino par l'émission de deux quarks, et la chargino se désintègre au LSP via l'émission d'un boson W-(SM 4);
• Paire-production de charginos, qui se désintègre directement sur ​​le LSP via l'émission d'un boson W-(SM 5).

La fraction d'événements mSUGRA classés comme appartenant à l'une de ces cinq modèles simplifiés est représenté sur la figure 5. Pour l'exemple mSUGRA, les approximations simplificatrices supplémentaires suivantes sont apportées: Lorsque le squark se désintègre à la gluino, la décroissance de la gluino est compté dans la classification de la topologie de l'événement, et la désintégration de la squark au gluino est compté comme un jet supplémentaire en cas («jets de plus»), comme si elle était identique à parapher ou rayonnement à l'état final. Lorsque le gluino se désintègre par un squarkiles/ftp_upload/50419/50419gtilde.jpg 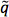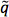"/> → q , → q Cependant, l'état final de la désintégration apparaît toujours comme si le gluino avait produit deux jets et pourri directement, en omettant le squark étape, sauver quelques (petites) différences de cinématique. Pour ces cas, par conséquent, la chaîne de désintégration est classé comme le gluino decayó via l'émission d'une paire de quark sans squark intermédiaire ( → qq ), Plutôt que de le classer comme la désintégration de squark avec unjet de rayonnement comme l'état initial final ou supplémentaire ( 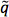→ q ainsi jet (s)). Associé production squark-gluino est divisé équitablement entre les Squark et gluino modèles simplifiés. Avec ces approximations, il est possible de classer une grande partie des événements supersymétriques comme l'un des cinq modèles simplifiés à l'étude. C'est la première étape vers la reconstruction de modèle.

La cinématique d'événements pour deux points de l'espace des paramètres mSUGRA, avec une combinaison de modèles simplifiés utilisés pour les imiter, sont présentés dans les figures 6, 7, et 8. Ces deux points sont décomposés en utilisant le procédé décrit ci-dessus, et les cinq modèles simplifiés sélectionnés et combinés sont construits en fonction des spectres de masse, les taux de production, etfractions de ramification des points. Les événements du modèle simplifié ont été générés et analysés d'une manière identique pour les événements mSUGRA. Ici, quatre des variables cinématiques clés utilisés dans les recherches de supersymétrie au LHC sont représentés: premier élan jet transversale (p _T), lepton p _T, énergie transverse manquante, et la masse effective, définie comme la somme scalaire des impulsions transverses des quatre principaux jets et le lepton. Deux caractéristiques sont visibles dans la masse effective, leader jet, et manquant distributions d'énergie transversales, correspondant à la production de la production et weakino forte. Dans ces distributions inclusives, certaines divergences sont clairement visibles. Le bas-p _T lepton queue, par exemple, est principalement de désintégrations tau qui ne sont pas couverts par l'un des modèles simplifiés. La faible consommation d'énergie transverse manquante, région de faible masse effective est en partie de la production associée LSP-X, qui n'est pas modélisé. La plupart des fonctions cinématiques sont décritsassez bien par PGS pour les fins d'une recherche dans un espace de paramètres avec la chute rapide de fond. Tau taux de faux demeurent un défi important pour une paramétrisation des résultats d'analyse de la protéine tau, et de traiter complètement cette question dépasse le cadre de ce protocole.

Toutefois, les réductions de la plupart des régions de signaux utilisés au LHC sont telles que des topologies de désintégration simples sont choisis au cours des événements de multiplicité souvent plus doux ou plus complexes. Ainsi, la sélection de la région de signal a tendance à améliorer la description de la cinématique des événements par des modèles simplifiés. Comparaison dans une région d'une seule leptonique similaire à celle utilisée dans une recherche récente ATLAS SUSY ¹⁶ sont présentées dans les figures 7 et 8. L'accord dans la forme et la queue est nettement meilleure. La cinématique des modèles simplifiés se comparent bien à la cinématique des modèles SUSY compris, ce qui suggère que l'efficacité et l'acceptation d'un point de SUSY complète peuvent être décritspar une combinaison limité de modèles simplifiés. Bien entendu, la cinématique du uniquement les événements SUSY correspondant à des topologies décrites par des modèles simplifiés sont identiques à leurs homologues des modèles simplifiés. Cela sert comme une confirmation que ces événements ne sont pas couverts par ces modèles simplifiés sont soit une petite fraction des événements au total ou cinématique semblables à ceux qui sont couverts. Ceci termine l'étape de reconstruction de modèle dans le cas d'mSUGRA.

La procédure de fixation de la limite prévue à l'article 3 est ensuite appliquée au plan mSUGRA avec β = tan 10, A ₀ = 0 et μ> 0, en utilisant les régions de signal de la recherche ATLAS zéro lepton ^16. Cinq régions de signal sont inclus dans cette recherche, et la région de signal à la limite prévue meilleur est utilisé pour chaque point. Un point est considéré comme étant exclu, si le nombre d'événements SUSY attendus dans la région de signal optimal est supérieur à un niveau de confiance de 95% observéelimite supérieure sur les nouveaux événements de la physique dans la région de signal. Les résultats de l'exclusion de modèle simplifié sont comparés à l'exclusion zéro lepton sans incertitudes systématiques sur le signal, comme indiqué précédemment, la figure 9. Quatre courbes d'exclusion de modèle simplifié sont présentés, correspondant aux équations 1 et 3-5. Par rapport à la limite d'exclusion zéro lepton, l'approche la plus conservatrice à base simplifiée-modèle fait plutôt mal dans la région dominée par 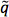et weakino associé production, manquant la limite correcte jusqu'à ~ 100 GeV. C'est aussi en partie due à la désintégration relativement complexe de la gluino (cf. le grand nombre de modes ouverts dans la figure 3). 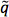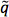La couverture est beaucoup plus proche de la vraie limitepour la région dominée par et production, pour lequel la limite de modèle dérivé est simplifiée dans les 40 GeV de la limite réelle.

Cette prescription omet le traitement des incertitudes théoriques sur le modèle de signal. En fait, les expériences du LHC a ne traitent pas ces incertitudes d'une manière cohérente, ni l'ensemble des incertitudes inclus. Aucune expérience, par exemple, comprend toute incertitude sur le calcul des masses visibles à partir des paramètres d'échelle de GUT. Les limites èmeà sont présentés ici, donc il faut s'attendre à différer des limites publiées. Dans la figure 10, les limites d'exclusion ATLAS publiés dans le canal zéro lepton sont comparés à ceux obtenus ici sans aucune incertitude systématique sur le signal. La limite sans incertitudes de signal est nettement plus élevé que la limite publiée. Pour le reste de l'article, la limite sans incertitudes systématiques sur le signal sera considéré comme la "bonne réponse" à être arrivé à l'aide de modèles simplifiés. L'incertitude théorique peut être ajoutée à la fois de la même façon et affectera les deux limites étant approximativement dans le même sens.

Afin de présenter les résultats réalisable avec les ressources présentes aussi précisément que possible, des points de modèle simplifié sont générés sur une grille correspondant à peu près à celui déjà utilisé par l'expérience ATLAS ^17. Entre ces points, Aε est interpolée dans le m en deux dimensionssquark / m _gluino = m grille _{de LSP.} Parce que SM 3 et SM 4 sont trois grilles dimensionnelles, et parce qu'il est peu probable que les expériences fourniront plein Aε trois dimensions, trois valeurs de masse chargino intermédiaire sont utilisés: m _chargino = x × (m _{squark / gluino} - m _LSP) + m _LSP, x = 0,25, 0,5, et 0,75. Pour interpoler entre ces trois plans bidimensionnels, un ajustement quadratique simple est utilisé. Lorsque vous approchez des limites de m _LSP = m et m _{chargino squark / gluino,} les modes de désintégration se tournent naturellement hors, ce qui interpolation plus compliqué inutile.

De la comparaison des courbes d'exclusion, on peut en effet voir que la limite d'exclusion conservateur réglé en utilisant l'équation. 1 suit la limite d'exclusion "correcte" très bien dans les régions de l'espace des phases qui sont bien couverts par le mode simplifiéls (cf Figure 5). Dans les régions qui ne sont pas aussi bien couverts, Eq. 3 fournit encore une limite conservatrice. La limite agressif fixé par Eq. 5 surestime l'exclusion jusqu'à 40 GeV dans la région de squark-dominé et par jusqu'à 100 GeV dans la région de gluino dominé l'espace des phases, parce que l'hypothèse que les longues chaînes de désintégration de gluino sont bien modélisé par les chaînes plus courtes de l' modèles simplifiés est invalide à un certain niveau. En termes de couverture paramètre-espace, les limites conservatrices sous couverture de 20%, les deux limites moyennes sous couverture de 10%, et la limite agressif sur-couvertures de 10%. Naturellement, l'élargissement du dictionnaire des modèles simplifiés disponibles améliorerait la limite conservatrice et réduire la limite agressif comme plus correcte Aε sont inclus pour plus de modes de production et de désintégration. Cependant, même avec ce petit nombre de modèles simplifiés, les limites fixées conservateur sont proche du résultat "corriger".

Pour des fins de démonstration, les limites sont également placés sur une région de signal mSUGRA à haute β bronzage. Les limites sont représentées sur la figure 11. Sur la base de l'accord observé dans la figure 10, l'exclusion expérimental devrait se situer un peu au-delà de l'exclusion prévue par l'équation. 3.

En extrapolant les théories plus exotiques, ou même dans l'expansion de l'applicabilité d'une petite liste des modèles simplifiés de Susy théories, plusieurs approximations peuvent être faites:

1. Que des jets lourds saveur sont identiques à jets d'arôme de lumière pour les recherches qui ne comprennent pas la saveur de marquage;
2. Que les photons sont identiques à jets de recherches qui ne s'identifient pas photons;
3. Que plus de la moitié du temps, chargino (neutralino) se désintègre à la LSP via l'émission d'un boson W-(boson Z) de produire une signature fonctionnellement identique à gluino se désintègre par émission de deux quarks.

Figure 1. Gauche, le Aε public pour la ATLAS trois jet de région "lâche" un lepton de signal ^17. Droite, la même reproduit dans le MadGraph + installation + Pythie PGS utilisé ici. Quelques différences sont à prévoir dans les différents générateurs et des statistiques plus élevées utilisées ici, mais les deux se succèdent de près. Cliquez ici pour agrandir la figure .

19/50419fig2highres.jpg "src =" / files/ftp_upload/50419/50419fig2.jpg "/>
Figure 2. Rapports de branchement pour les mécanismes de production de SUSY et les modes de désintégration dans l'espace des paramètres mSUGRA. La rangée supérieure (m ₀ = 300 GeV, m _1/2 = 600 GeV, tan (β) = 10, A ₀ = 0 GeV, et μ> 0 ) est typique de la région dans l'espace de paramètre qui est dominée par la production de squark, et la ligne du bas (m ₀ = 1.000 GeV, m _1/2 = 350 GeV, tan (β) = 10, A ₀ = 0 GeV, et μ > 0) est typique pour la région dans l'espace des paramètres se trouvant dans un peu entre les deux extrêmes. Pour plus de clarté, des modes de production et de décroissance ne sont inscrites si leur fraction ramification est supérieure à 0,5%. Les labels "SM" avec un certain nombre sont donnés à des modes de décroissance correspondant aux modèles simplifiés discutés dans le protocole de reconstruction de modèle.les/ftp_upload/50419/50419fig3large.jpg "target =" _blank "> Cliquez ici pour agrandir la figure.

Figure 3. Rapports de branchement pour les mécanismes de production de SUSY et les modes de désintégration dans l'espace des paramètres mSUGRA. La rangée supérieure (m ₀ = 300 GeV, m _1/2 = 500 GeV, tan (β) = 25, A ₀ = 1.500 GeV, et μ> 0) est typique de la région dans l'espace de paramètre qui est dominée par la production de squark, et la ligne du bas (m ₀ = 2100 GeV, m _1/2 = 100 GeV, tan (β) = 45, A ₀ = 500 GeV , et μ> 0) est typique pour la région dominée par la production de gluino. Pour plus de clarté, les modes de production et de désintégration ne sont indiquées sileur fraction de branchement est supérieure à 0,5%. Les labels "SM" avec un certain nombre sont donnés à des modes de décroissance correspondant aux modèles simplifiés discutés dans le protocole de reconstruction de modèle. Les modèles dans les régions blancs n'avaient pas les événements décrits par des modèles simplifiés, avec des statistiques Monte Carlo limitées. Cliquez ici pour agrandir la figure .

Figure 4. Variation des rapports de branchement, en pour cent, des principaux modes de production de SUSY et désintégration dans l'espace des paramètres mSUGRA avec tan (β) = 10, A ₀ et μ> 0. L'angle supérieur droit, où les sparticules forts sont lourd, comprend un contr importante ibution de production weakino. Les modèles dans les régions blancs n'avaient pas les événements décrits par des modèles simplifiés, avec des statistiques Monte Carlo limitées. Cliquez ici pour agrandir la figure .

Figure 5. Le pourcentage d'événements mSUGRA classés comme appartenant à l'un des cinq modèles simplifiés examinés dans le présent document, à faible tan (β) (à gauche) et de haute tan (β) (à droite). Cliquez ici pour agrandir la figure .

419fig6highres.jpg "src =" / files/ftp_upload/50419/50419fig6.jpg "/>
Figure 6. Cinématique d'un point mSUGRA squark-production-dominé (m ₀ = 300 GeV, m _1/2 = 600 GeV, tan (β) = 10, A = ₀ 0 GeV, et μ> 0) et un ensemble de cinq modèles simplifiés construits en utilisant le même spectre de masse. aiguilles d'une montre à partir du haut à gauche, conduisant jet p _T, leader muon p _T, masse effective, et énergie transverse manquante. Pas de sélection de signal a été appliquée. Cliquez ici pour agrandir la figure .

Figure 7. Cinématique d'un squark-producteursction dominé point de mSUGRA (m ₀ = 300 GeV, m _1/2 = 600 GeV, tan (β) = 10, A = ₀ 0 GeV, et μ> 0) et un ensemble de cinq modèles simplifiés construits en utilisant la même masse spectre. aiguilles d'une montre à partir du haut à gauche, conduisant jet p _T, leader muon p _T, masse effective, et énergie transverse manquante. Une sélection de signal similaire à celui-lepton-quatre jets recherche "serré" ATLAS SUSY a été appliquée. Cliquez ici pour agrandir la figure .

Figure 8. Cinématique d'un point mSUGRA complexe (m ₀ = 1.000 GeV, m _1/2 =350 GeV, tan (β) = 10, A = ₀ 0 GeV, et μ> 0) et un ensemble de cinq modèles simplifiés construit en utilisant le même spectre de masse. Aiguilles d'une montre à partir du haut à gauche, conduisant jet p _T, leader muon p _T , masse effective, et de l'énergie transverse manquante. Une sélection de signal similaire à celui-lepton-quatre jets recherche "serré" ATLAS SUSY a été appliquée. Cliquez ici pour agrandir la figure .

Figure 9. Combiné limites d'exclusion de zéro pour les modèles leptons mSUGRA avec tan β = 10, A = ₀ et μ 0> 0 (10a) par rapport à la limite d'exclusionobtenus à l'aide de modèles simplifiés uniquement (10b). La région de signal fournissant la limite meilleure attendu est prise pour un point donné dans l'espace des paramètres. La limite de 95% de niveau de confiance attendu est représenté par une ligne pointillée bleue, et la limite observée est représentée par une ligne rouge solide. Les résultats de recherches sont également présentés aux fins de comparaison ^42-48, bien que certaines de ces limites ont été produites à l'aide des choix de paramètres légèrement différents. Les limites des modèles simplifiés sont générées en utilisant quatre séries d'hypothèses, correspondant aux équations limites dans le texte principal. Cliquez ici pour agrandir la figure .

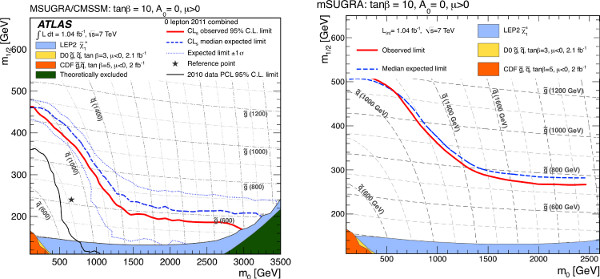
Figure 10. Combinés limites d'exclusion zéro leptons pourModèles mSUGRA avec β tan = 10, A ₀ = 0 et μ> 0 ¹⁶ (à gauche) en comparaison avec la limite d'exclusion obtenue en utilisant PGS et sans incertitude systématique sur le signal. La région de signal fournissant la meilleure limite attendue est pris pour un point donné dans l'espace des paramètres. La limite de 95% de niveau de confiance attendu est représenté par une ligne pointillée bleue, et la limite observée est représentée par une ligne rouge solide. Les résultats de recherches sont également présentés aux fins de comparaison ^42-48, bien que certaines de ces limites ont été produites à l'aide des choix de paramètres légèrement différents. Cliquez ici pour agrandir la figure .

Figure 11. limites d'exclusion pour les modèles mSUGRA avec β tan = 40, A ₀ = -500 GeV et μ> 0 (à gauche) et β tan = 20, A ₀ = 500 GeV et μ> 0 (à droite) obtenus en utilisant des modèles simplifiés ne . Limites combinées sont obtenus en utilisant la région de signal qui génère la meilleure limite prévue au niveau de chaque point de l'espace des paramètres. Les limites des modèles simplifiés sont générées en utilisant quatre séries d'hypothèses, correspondant aux équations limites dans le texte principal. Cliquez ici pour agrandir la figure .

L'application des limites des modèles simplifiés pour produire un contour d'exclusion dans un nouveau modèle complet de la physique a été démontrée. Malgré la complexité apparente de mSUGRA points de l'espace des paramètres, la cinématique peut être bien reproduits par une combinaison de seulement un petit nombre de modèles simplifiés. L'accord cinématique est encore améliorée lors de la recherche dans une région particulière du signal, depuis les recherches menées à ce jour au LHC ont tendance à favoriser simplifiées événement topologies de modèle comme avec un (relativement) petit nombre d'objets _{de T-haute} p.

Les contours d'exclusion dérivés de modèles simplifiés se comparent favorablement à ceux déjà publiés par des recherches spécifiques. Avec cette procédure, il est possible de refondre trivialement résultats d'exclusion dans les théories supersymétriques plus exotiques, ou même dans les théories nonSUSY avec signatures couverts par des modèles simplifiés. Cette méthode permet en outre une voie simple pour la conservation des données d'unend application des recherches actuelles théories futures.

Pratiquement, cette approche signifie une économie pour les expériences LHC et un grand avantage pour les théoriciens et les phénoménologues LHC ressource importante. Par la refonte des théories en utilisant les informations disponibles à partir de l'élément de matrice et les probabilités de désintégration, pas de simulation de calcul intensif du modèle doit être fait. Au lieu de cela, les expériences sont libres de fournir des résultats carrément d'exclusion dans une grande variété de modèles théoriques qui incluent - mais ne peut pas être complètement couverts par - signatures d'état simples finales. De même, les théoriciens n'ont pas besoin d'attendre que les expériences du LHC pour produire des limites dans leur modèle privilégié. Bien que les modèles simplifiés ne peuvent pas couvrir tous les modes de production et de désintégration d'un modèle, avec un nombre relativement restreint de modèles simplifiés, il est possible de couvrir un éventail assez large de possibilités. Les exclusions acquises de cette manière ne se chevauchent pas avec précision les résultats d'une expérience complèteRecherche mentale. Dans la recherche ère actuelle du LHC, mais ils donnent une estimation critique et étonnamment précise de la quantité d'espace de la théorie a déjà été exclu par les recherches déjà menées, et combien peuvent encore être ouverts à la découverte.

Les auteurs sont à la fois membres de la collaboration ATLAS. Cependant, pas de ressources internes ATLAS, monétaires ou non monétaires, ont été utilisés dans la réalisation de ce travail.

Les auteurs tiennent à remercier Jay Wacker de discussion important de modèles simplifiés et les pièges potentiels. Merci aussi à Max Baak et Till Eifert pour la critique constructive et d'encouragement à chaque fois qu'il était nécessaire. Merci au Programme d'été pour étudiants du CERN pour faire de cette collaboration possible.