Approximate Number Sense Test

Source: Laboratory of Jonathan Flombaum—Johns Hopkins University

A common carnival game is to ask people to guess the number of jellybeans packed into a jar. The chances that anyone will get the exact number right are low. But what about the chances that someone will guess 17 or 147,000? Probably even less than the chances of guessing the correct answer; 17 and 147,000 just seem irrational. Why? After all, if the beans cannot be taken out and counted one-at-a-time, how can someone tell that an estimate is too high or too low?

It turns out that in addition to verbal counting (something clearly learned), people appear to possess hardwired mental and neural mechanisms for estimating numbers. To put it colloquially, it is what might be called an ability to guesstimate, or “ballpark.” Experimental psychologists call it the “Approximate Number Sense,” and recent research with an experimental paradigm of the same name has begun to uncover the underlying computations and neural mechanisms that support the ability to guesstimate.

This video demonstrates standard procedures for investigating nonverbal numerical estimation with the Approximate Number Sense Test.

1. Stimuli and trials

1. Program the experiment in Psychopy, MATLAB, or something similar (a free version can also be downloaded for non-commercial uses at www.panamath.org).
2. Design all trials in the experiment to look more or less the same.
   1. Divide the display in half. Use a grey background.
   2. One side of the display shows a collection of blue circles.
   3. The other side shows a collection of yellow circles.
3. Draw the circles in different sizes, as shown in the sample trial (Figure 1).
   
   Figure 1. Schematic depiction of a single trial of the approximate number sense test. On each trial, the participant reports whether he saw more blue or yellow dots.
4. The key manipulation involves the number of yellow and blue circles. There should always be more of one kind than the other. The difference should be characterized in terms of a ratio: 2:1, 1.75:1, 1.5:1, 1.35:1, 1.25:1, and 1.15:1.
5. Instruct the program to produce 20 trials with each ratio.
   1. Randomly select the larger color.
   2. Randomly select the smaller number of circles.
   3. Select the larger number to make the desired ratio.
   4. Draw yellow circles on one side of the display.
   5. Draw blue circles on the other side.
   6. Randomly choose the radius of each circle between 1° (of visual angle) and 3.5°.
6. On each trial, a display appears for 500 ms. After it disappears, the participant presses the ‘Y’ key if they think they saw more yellow dots, or the ‘B’ key if they think they saw more blue dots.
7. Provide feedback after each trial with a screen that displays either “Correct!” or “Incorrect.”

To graph the results from a participant, average performance as a function of the ratio on each trial (Figure 2). For example, across all 20 trials with a ratio of 2:1, in what fraction did the participant supply the right answer?

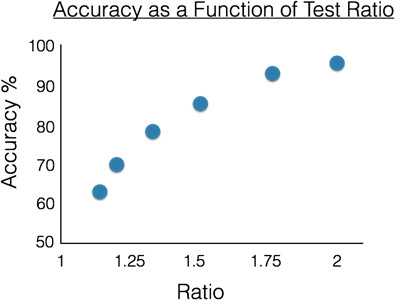
Figure 2. Sample results from a single participant in the approximate number test. Performance, measured as response accuracy, increases as the ratio difference between the larger and smaller set of dots increases. Since the participant makes a binary choice—yellow or blue bigger—chance is 50%.

Performance, measured as response accuracy, increases as the ratio difference between the larger and smaller set of dots increases. Since the participant makes a binary choice—yellow or blue bigger—chance is 50%. Note that the participant’s performance improves as the ratio difference increases. But the function is not linear, since there is a ceiling of 100% on how well one can do. The fact that performance is ratio-constrained suggests that numerical approximation is controlled by an analog or magnitude-like mechanism. An analogy is useful here. Imagine representing two quantities by dropping a fistful of sand into a bucket for each dot seen, one bucket for yellow dots and one for blue dots. It is very unlikely that you would deposit the same amount of sand in the buckets on each drop. So say one bucket represents four dots—it has four handfuls of sand in it. And the other represents eight dots—it has eight handfuls of sand. You could weigh the buckets, and easily know which was meant to represent more dots. But now imagine that the larger bucket was only meant to represent five dots—it has only five handfuls of sand it. It will probably still weigh more than the bucket with four, but not by a lot. And because you may sometimes grab a little more sand, and sometimes a little less, there might even be occasions where the bucket meant to represent four ends up weighing more! This is an analog system. The representation—in this case, sand mass—does a good job of capturing large proportional differences between represented quantities, but because of noise, small differences can be hard to tell apart.

The result is that such systems are ratio-constrained. The ability to tell apart more or less depends on the ratio difference between the quantities, not the subtractive difference. It’s as easy to tell apart eight and four as it is eight and sixteen. On the other hand, eight versus twelve is more difficult, even though it subtracts to a difference of four as well.

People differ between one another considerably in terms of the acuity of their approximate number sense. To characterize differences between individuals, experimental psychologists generally test to find the smallest ratio a person can tell apart with 75% accuracy. As shown in Figure 2, it is a ratio somewhere between 1.25 and 1.5. This number is just a quick way of summarizing how acute an approximate number sense a person has. But beyond the fact that there are large differences between people—one person might have a ratio of 1:1 and another might have a ratio of 1:4, for example—these differences correlate significantly with formal math ability. For instance, 75%-correct ratios in young children correlate with arithmetic abilities as measured by standardized tests. This is surprising, because ultimately, arithmetic is not about estimating. However, these kinds of correlations suggest that formal math ability depends on an underlying approximate number sense.