질량 보존 및 유속 측정
Overview
출처: 리카르도 메지아 알바레즈와 후삼 히크마트 자바, 기계 공학과, 미시간 주립 대학, 이스트 랜싱, MI
본 실험의 목적은 제어부피(CV) 제형[1, 2]을 이용하여 유량계로서 유량계의 보정을 입증하는 것이다. CV 분석은 상세한 차동 해석을 통해 달성할 수 있는 상세한 설명이 아니라 엔지니어링 시스템에 대한 흐름의 거시적 효과에 초점을 맞추고 있습니다. 이력서 분석을 통해 엔지니어에게 유량 시스템을 설계할 때 추구할 경로에 대한 초기 기반을 제공하기 때문에 이러한 두 가지 기술은 상호 보완적인 접근 법으로 간주되어야 합니다. 대체로, CV 분석은 엔지니어에게 시스템에서 지배적인 질량 교환에 대한 아이디어를 제공하고, 이상적으로 차동 제형을 통해 상세한 설계 또는 분석을 추구하기 전에 취해야 할 초기 단계가 되어야 한다.
대량 보존을 위한 CV 제제의 주요 원리는 제어 표면(CS)으로 알려진 것에 동봉된 단순화된 부피에 의해 유동 시스템의 세부 정보를 대체하는 것이다. 이 개념은 가상이며 분석을 영리하게 단순화하기 위해 자유롭게 정의 할 수 있습니다. 예를 들어 CS는 지배적인 속도에 수직으로 입구와 콘센트 포트를 '잘라'해야 합니다. 그런 다음, 분석은 CS를 통해 순 질량 플럭스와 CV 내부의 질량 변화 속도 사이의 균형을 찾는 것으로 구성됩니다. 이 기술은 유량계로서 원활한 수축의 보정으로 입증될 것이다.
Principles
제어 부피(CV)는 시스템에서 질량의 균형을 연구하기 위해 임의로 정의된 제어 표면(CS)이라고 불리는 가상의 폐쇄된 표면에 의해 정의됩니다. 도 1A는 흐름 통로를 통과하는 흐름 영역을 포함하는 제어 부피의 예를 나타낸다. 통로 내부의 대량 유입, 유출, 변화 속도에 대한 대책을 얻는 데만 관심이 있기 때문에 통로의 흐름에 대한 세부 사항은 무관합니다. 이러한 모든 효과는 일체형 형태로 질량 보존을 위한 방정식으로 요약할 수 있습니다[1, 2]:
 (1)
(1)
방정식(1)의 오른쪽에 있는 첫 번째 용어는 제어 부피 내부의 질량 변화 속도를 나타내고, 두 번째 용어는 제어 표면을 통해 질량의 순 플럭스를 나타낸다. 벡터 차이는 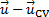 CV와 흐름 사이의 상대적 속도이며,
CV와 흐름 사이의 상대적 속도이며,  벡터는 영역 차등에 대한 외부 정상 단위이다. 상대 속도 사이의 도트 생성물은
벡터는 영역 차등에 대한 외부 정상 단위이다. 상대 속도 사이의 도트 생성물은  CS를 교차하는 속도 구성 요소를 나타내며, 이후부터질량교환에 기여한다. 이 점 제품의 징후는 질량 플럭스가 CV로 향하고 CV에서 멀리 지시되는 긍정적 인 경우 음수입니다.
CS를 교차하는 속도 구성 요소를 나타내며, 이후부터질량교환에 기여한다. 이 점 제품의 징후는 질량 플럭스가 CV로 향하고 CV에서 멀리 지시되는 긍정적 인 경우 음수입니다.

그림 1. 기본 구성의 Sc헤매틱. (A) 원심 팬을 위한 부드러운 섭취. 제어 볼륨은 통로의 내부 프로파일로 정의됩니다. 솔리드 벽은 컨트롤 볼륨에서 제외되지만 경계 조건은 제어 표면에 유지됩니다(예: 침투 및 미끄러짐 없음). 포트 1은 통로의 입구 쪽으로 정의되며 포트 2는 피토 튜브의 끝과 일치하는 단면 평면으로 정의됩니다. 흐름은 왼쪽에서 오른쪽으로 이동합니다. (B) 데이터 수집 시스템의 피토 정적 시스템과 스키마티c. 이 그림의 더 큰 버전을 보려면 여기를 클릭하십시오.
본 데모의 경우, 고정 된 이력서가 원심 팬의 섭취시 부드러운 수축의 윤곽을 따르는 그림 1A에 표시된 구성이 있습니다. 이 CV를 통한 흐름은 안정적이므로 제어 볼륨 내부의 질량 변화 속도는 0입니다. 따라서, 방정식 (1)의 오른쪽에 있는 첫 번째 용어는 사라집니다. 또한, CV는 공간에 고정되어 속도가 없는 수축에 부착되어 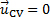 있습니다. 따라서 이 CV를 통한 질량의 순 플럭스는 0이고 방정식(1)은 다음과 같은 단순화됩니다.
있습니다. 따라서 이 CV를 통한 질량의 순 플럭스는 0이고 방정식(1)은 다음과 같은 단순화됩니다.
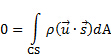 (2)
(2)
도 1A의 구성을 고려할 때, 질량은 포트 1을 통해 CV로 흐르고 포트 2를 통해 CV를 남깁니다. 따라서, 방정식(2)의 오른쪽에 있는 표면 일체형은 각 포트에 대해 하나씩 두 개의 독립적인 일체로 나눌 수 있다. 도트 생성물의 표시는 흐름이 CV쪽으로 이동하기 때문에 포트 1에서 음수이며, 흐름이 CV에서 멀어지기 때문에 포트 2에서 양수입니다. 속도가 어느 포트에 균일하게 분포되어 있다고 가정하지 않고, 점 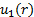
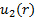 제품을 복용한 후에도 둘 다 남아 있다는 점을 고려하여 각각의 속도 프로파일을 만들어 봅시다. 즉, 영역 벡터와 평행한 속도 구성 요소의 크기,
제품을 복용한 후에도 둘 다 남아 있다는 점을 고려하여 각각의 속도 프로파일을 만들어 봅시다. 즉, 영역 벡터와 평행한 속도 구성 요소의 크기,  . 마지막으로, 수축을 따라 압력 변화는 밀도의 관찰 가능한 변화를 유도하기에 충분하지 않습니다. 이제부터 밀도를 일정하게 고려할 수 있습니다. 이러한 상황에서 방정식(2)은 다음을 단순화합니다.
. 마지막으로, 수축을 따라 압력 변화는 밀도의 관찰 가능한 변화를 유도하기에 충분하지 않습니다. 이제부터 밀도를 일정하게 고려할 수 있습니다. 이러한 상황에서 방정식(2)은 다음을 단순화합니다.
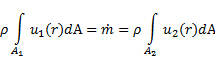 (3)
(3)
질량이 보존되기 때문에 질량 플럭스는  두 포트를 통해 동일합니다. 이러한 관계의 구조를 감안할 때, 방정식 (3)의 각 일체형은 해당 포트를 통해 체적 유량을
두 포트를 통해 동일합니다. 이러한 관계의 구조를 감안할 때, 방정식 (3)의 각 일체형은 해당 포트를 통해 체적 유량을  표현하며,이 사실은 지정된 포트에 대한 평균 속도를 정의하는 데
표현하며,이 사실은 지정된 포트에 대한 평균 속도를 정의하는 데  도움이됩니다.
도움이됩니다.
 (4)
(4)
비스타한 조건에서 포트 2의 속도는 중앙 유선형을 따라 Bernoulli의 방정식을 사용하여 섭취 이외의 조건의 관점에서 표현 될 수 있습니다 (참조 그림 1A 참조) :
 (5)
(5)
여기서, 높이의 효과는 수평이기 때문에 중앙 유선형에 사라지고, 유체가 공기이기 때문에 다른 유선형에서는 무시할 수 있으며, 이는 매우 작은 특정 중량을 갖는다. 또한 중앙 유선형의 초기 점은 속도가 0이라는 입구에서 충분히 멀리 떨어져 있습니다. 방정식(5)이 이상화된 비동기 케이스에 대한 것이라는 점을 감안할 때, 이 속도값은 포트 2에서 모두 동일합니다. 실제로 경계 층 성장은 속도 프로파일에 영향을 미치고 균일하지 않습니다. 이러한 효과를 고려하기 위해 이상적인 추정은 "방전 계수"를 통한 실험 측정과 비교됩니다. 이 계수는 유량의 지정된 단면에 대해 측정된 평균 속도와 비하 속도 사이의 비율로 정의됩니다.
 (6)
(6)
방전 계수는  형상 및 레이놀즈 번호에 따라 다릅니다. 일단
형상 및 레이놀즈 번호에 따라 다릅니다. 일단  결정되면, 방정식 (4) 및 (5)와 함께 단면 면적 및 측정하기 쉬운 압력 차동에 따라 포트 2의 유량을 결정하는 데 사용할 수 있습니다.
결정되면, 방정식 (4) 및 (5)와 함께 단면 면적 및 측정하기 쉬운 압력 차동에 따라 포트 2의 유량을 결정하는 데 사용할 수 있습니다.
 (7)
(7)
방정식(4), (5) 및 (6)를 함께 넣고 포트 2가 원형이라는 점을 고려할 때 다음 의 관계를  얻습니다.
얻습니다.
 (8)
(8)
방정식 (8)에서 속도 프로파일에 대한 지식이 방전 계수를 얻기 위해 필요하다는 것은 분명합니다. 정적 프로브 - 이 것을 위해, 우리는 피토에 의해 속도 측정을 사용합니다. 도 1B에 도시된 바와 같이, 피토 튜브는 지정된 지점에서 정적 및 동적 압력을 첨가하는 총 압력을  감지하는 정지로 흐름을 제공합니다. 반면, 벽의 정적 프로브는 정적 압력을 단독으로 감지합니다. 주어진 방사형 위치에 적용된 베르누이의 방정식에서 총 압박은 베르누이의 일정에 불과합니다. 포트 2에서 이 원리는 임의의 방사형 위치에서 다음 관계로 표현할 수 있습니다.
감지하는 정지로 흐름을 제공합니다. 반면, 벽의 정적 프로브는 정적 압력을 단독으로 감지합니다. 주어진 방사형 위치에 적용된 베르누이의 방정식에서 총 압박은 베르누이의 일정에 불과합니다. 포트 2에서 이 원리는 임의의 방사형 위치에서 다음 관계로 표현할 수 있습니다.
 (9)
(9)
여기서 우리는 유동 통로가 수평이기 때문에 수직 위치의 효과를 무시하고 있습니다. 요약하면 파이프 내에서 지정된 위치'r'에서속도의 크기에 대한 다음 관계를 얻습니다.
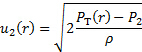 (10)
(10)
압력 차이는  도 1B에 묘사된 압력 트랜스듀서에 의해 직접 측정되며, 속도 프로파일은 파이프의 방사형 좌표를 따라 피토 튜브를 횡단함으로써 얻어진다. 이러한 속도 측정은 개별 위치에서 수행되므로 이러한 데이터 포인트는 사다리꼴 또는 Simpson규칙 [1]을 사용하여 방정식(8)의 일체성을 숫자로 해결하는 데 사용해야 합니다. 이 일체형의 값이 얻어지면,
도 1B에 묘사된 압력 트랜스듀서에 의해 직접 측정되며, 속도 프로파일은 파이프의 방사형 좌표를 따라 피토 튜브를 횡단함으로써 얻어진다. 이러한 속도 측정은 개별 위치에서 수행되므로 이러한 데이터 포인트는 사다리꼴 또는 Simpson규칙 [1]을 사용하여 방정식(8)의 일체성을 숫자로 해결하는 데 사용해야 합니다. 이 일체형의 값이 얻어지면,  특정 유동 조건에 대한 값을 얻기 위해, 덕트의 측정값, 밀도 및 반경의 측정값과 함께 방정식(8)에 연결되어야
특정 유동 조건에 대한 값을 얻기 위해, 덕트의 측정값, 밀도 및 반경의 측정값과 함께 방정식(8)에 연결되어야  한다. 서로 다른 흐름 조건에 대한 이 실험을 반복하면, 우리는 관계와 사이의 관계를 결정하는 데 사용할 수있는 분산 플롯을 얻을 것이다
한다. 서로 다른 흐름 조건에 대한 이 실험을 반복하면, 우리는 관계와 사이의 관계를 결정하는 데 사용할 수있는 분산 플롯을 얻을 것이다 
 . 그런 다음 이 관계는 방정식(7)으로 대체되어 유량을 완전히 결정할 수 있으며, 전적으로 의 함수로 할 수
. 그런 다음 이 관계는 방정식(7)으로 대체되어 유량을 완전히 결정할 수 있으며, 전적으로 의 함수로 할 수 
 있습니다.
있습니다.
Procedure
1. 시설 설정
- 시설에 흐름이 없는지 확인합니다.
- 데이터 수집 시스템이 그림 1B의회로도를 따르는지 확인합니다.
- 압력 변환기 #1 양포 포트를 연결하는 피토 튜브(참조용 도 1B
 참조)에 연결합니다.
참조)에 연결합니다. - 이 동일한 압력 변환기의 음수 포트를 섭취 통로()의 정적 프로브에
 연결합니다. 따라서,이 압력 변환기의 판독은 직접
연결합니다. 따라서,이 압력 변환기의 판독은 직접  ()될 것입니다.
()될 것입니다. - 볼트에서 파스칼(파스칼)으로 변환하는 이 변환 인자를
 기록합니다. 표 1에 이 값을 입력합니다.
기록합니다. 표 1에 이 값을 입력합니다. - 티를 사용하여 압력 변환기 #2 양포 포트(참조도 1B 참조)를 섭취 통로()의 정적
 프로브에 연결합니다.
프로브에 연결합니다. - 압력 변환기의 음의 포트를 대기()#2 열어
 둡니다. 따라서,이 트랜스듀서의 판독은 직접
둡니다. 따라서,이 트랜스듀서의 판독은 직접  ()가 될 것입니다.
()가 될 것입니다. - 볼트에서 파스칼(파스칼)으로 변환하는 이 변환 인자를
 기록합니다. 표 1에 이 값을 입력합니다.
기록합니다. 표 1에 이 값을 입력합니다. - 총 500개의 샘플(예: 데이터 5s)에 대해 데이터 수집 시스템을 100Hz 의 속도로 샘플링하도록 설정합니다.
- 데이터 수집 시스템의 채널 1이 압력 트랜스듀서 #1()에 해당하는지
 확인합니다.
확인합니다. - 데이터 수집 시스템의 변환 계수를
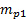 입력하여 압력
입력하여 압력  측정()이 파스칼로 직접 변환되는지 확인합니다.
측정()이 파스칼로 직접 변환되는지 확인합니다. - 여행 이 끝날 때 Pitot 프로브를 설정하여 파이프의 벽에 닿습니다. 프로브의 직경이 2mm이기 때문에 첫 번째 속도 지점은 벽에서 1mm 떨어진 방사형 좌표에 있습니다. 즉, 음의 방사형 위치에서
 (여기,
(여기,  mm).
mm).

그림 2. 실험 설정. (A): 연구 하에 흐름 통로. (B): 피토 튜브에 대한 수동 횡단 시스템. 이 그림의 더 큰 버전을 보려면 여기를 클릭하십시오.
표 1. 실험 연구를 위한 기본 매개 변수입니다. 파 1meter 값
| 매개 변수 | 값 |
| 유동 통로 반경(Ro) | 82.25 mm |
| 트랜스듀서 #1 교정 상수(m_p1) | 136.015944 Pa/V |
| 트랜스듀서 #2 교정 상수(m_p2) | 141.241584 N/V |
| 현지 대기압 | 100,474.15 Pa |
| 현지 온도 | 297.15 K |
| P_atm P_2 | 311.01 Pa |
2. 측정
- 흐름 시설을 켭니다.
- 디지털 멀티미터에서 볼트에서 압력 변환기 #2 판독값을 기록합니다.
- 표 1에 이 값을
 입력하고 값을 사용하여 볼트에서 파스칼로 판독값을 변환합니다.
입력하고 값을 사용하여 볼트에서 파스칼로 판독값을 변환합니다. 
- ()의 판독값을 기록하기 위해 데이터 수집 시스템을
 사용합니다.
사용합니다. - 표 2의 값을
 입력합니다.
입력합니다. - 표 2에서 제안된 값에 따라 피토 튜브의 방사형 위치를 변경하려면 횡단 노브를 사용합니다.
- 표 2가 완전히 채워지날 때까지 2.4 및 2.6 단계를 반복합니다.
- 시스템의 방전을 변경하여 유량을 변경합니다.
- 적어도 10개의 다른 유량에 대해 2.4~ 2.8단계를 반복합니다.
- 흐름 시설을 끕니다.

그림 5. 실험 설정. 천포판은 유동 시스템의 배출시 흐름을 제한한다. 이 그림의 더 큰 버전을 보려면 여기를 클릭하십시오.
표 2. 대표적인 결과. 속도 측정. r (mm) PT - P2 (Pa) u (r) (m / s
| r(mm) | PT - P2 (Pa) | u(r) (m/s) |
| 2.25 | 300.35 | 22.34 |
| 12.25 | 302.84 | 22.43 |
| 22.25 | 305.82 | 22.54 |
| 32.25 | 302.34 | 22.41 |
| 42.25 | 294.88 | 22.13 |
| 52.25 | 295.37 | 22.15 |
| 62.25 | 292.88 | 22.06 |
| 68.25 | 293.63 | 22.09 |
| 72.25 | 294.13 | 22.10 |
| 75.25 | 299.60 | 22.31 |
| 77.25 | 293.13 | 22.07 |
| 79.25 | 284.67 | 21.75 |
| 80.25 | 256.31 | 20.63 |
| 81.25 | 198.33 | 18.15 |
3. 데이터 분석.
- 표 2에서 압력 차이 값PT - P 2를 사용하여 속도프로파일을 결정합니다. 표 2에 결과를 입력합니다.
- 표 2의 압력 및 속도 값을 반경을
 사용하여, abscissas(그림3)로플롯합니다.
사용하여, abscissas(그림3)로플롯합니다. - 표 2의 속도 및 반지름 값을 기준으로 방정식(8)의 일체수를 계산합니다.
- 방정식(8)을 사용하여 각 유량에 대한 방전 계수를 계산합니다.
- 압실시스로 사용하여 방전 계수를
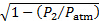 플롯합니다.
플롯합니다. - 방전 계수에 기능을 맞추어, 전력법은 좋은 선택입니다.

그림 3. 대표적인 결과. (A): 유동 통로의 방사형 좌표를 따라 정적 압력을 측정하는 예. (B): 정적 압력의 측정에서 결정된 속도 분포. 이 그림의 더 큰 버전을 보려면 여기를 클릭하십시오.
Results
팬의 방전시 흐름의 주어진 제한에 대해, 도 3A는  피토 튜브로 횡단한 후 파이프 내부의 다른 방사형 위치에서 동적 압력() 측정을 나타낸다. 이러한 값은 이러한 방사형 위치에서 로컬 속도를 결정하는 데 사용되었으며 결과는 그림 3B에표시됩니다. 이러한 데이터에 사다리꼴 규칙을 사용하여 평균 속도에 대한 방정식(4)을 해결한 후
피토 튜브로 횡단한 후 파이프 내부의 다른 방사형 위치에서 동적 압력() 측정을 나타낸다. 이러한 값은 이러한 방사형 위치에서 로컬 속도를 결정하는 데 사용되었으며 결과는 그림 3B에표시됩니다. 이러한 데이터에 사다리꼴 규칙을 사용하여 평균 속도에 대한 방정식(4)을 해결한 후  m/s값을 얻었습니다. 한편,
m/s값을 얻었습니다. 한편,  표 1의 값은 방정식(5)으로부터의 이상적인 속도를 결정하는 데 사용되었기
표 1의 값은 방정식(5)으로부터의 이상적인 속도를 결정하는 데 사용되었기  때문에, 따라서, 이 흐름 조건에 대한 방전 계수는 다음과
때문에, 따라서, 이 흐름 조건에 대한 방전 계수는 다음과 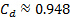 이다. 이 값은 그림 4에 빨간색 삼각형으로 표시됩니다.
이다. 이 값은 그림 4에 빨간색 삼각형으로 표시됩니다.
이 실험을 29번 더 반복한 후 도 4에도시된 분산 플롯을 얻었다. 이 데이터는 다음과 같은 전원 법칙으로 잘 표현될 수 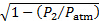 있습니다.
있습니다.
 (11)
(11)
이러한 인수를 선택하는 이유는 선행 상수가 차원이 없는 상태로 유지되도록 하기 위해서이므로 압력에 사용되는 단위 시스템에 관계없이 이러한 상관 관계가 여전히 유효하도록 하기 때문입니다. 이 함수는 수학식(7)으로 대체되어 유량을 다음과 같은 함수로 얻을 수  있습니다.
있습니다.
 (12)
(12)
여기서, 방정식 (7)과 (11)의 모든 상수는 단일 차원없는 상수로 덩어리했다 : 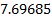 . 따라서, 방정식(12)은 변수가 해당 단위에 일관되게 할당되는 한 모든 단위 시스템에 유효합니다. 편의를 위해, 방정식(7)으로부터의 밀도는 이상적인 가스법을 사용하여 대기압 및 절대 온도의 관점에서 표현되었다. 수학식(12)은 국부압력및온도(T및 PATM)의변화를 차지하기 때문에 다양한 대기 조건에 유효합니다. 또한 기하학적 유사성이 보존되는 한 이 방정식은 반지름 R에서 차지하는 다양한 크기의 구절에 유효합니다.
. 따라서, 방정식(12)은 변수가 해당 단위에 일관되게 할당되는 한 모든 단위 시스템에 유효합니다. 편의를 위해, 방정식(7)으로부터의 밀도는 이상적인 가스법을 사용하여 대기압 및 절대 온도의 관점에서 표현되었다. 수학식(12)은 국부압력및온도(T및 PATM)의변화를 차지하기 때문에 다양한 대기 조건에 유효합니다. 또한 기하학적 유사성이 보존되는 한 이 방정식은 반지름 R에서 차지하는 다양한 크기의 구절에 유효합니다.
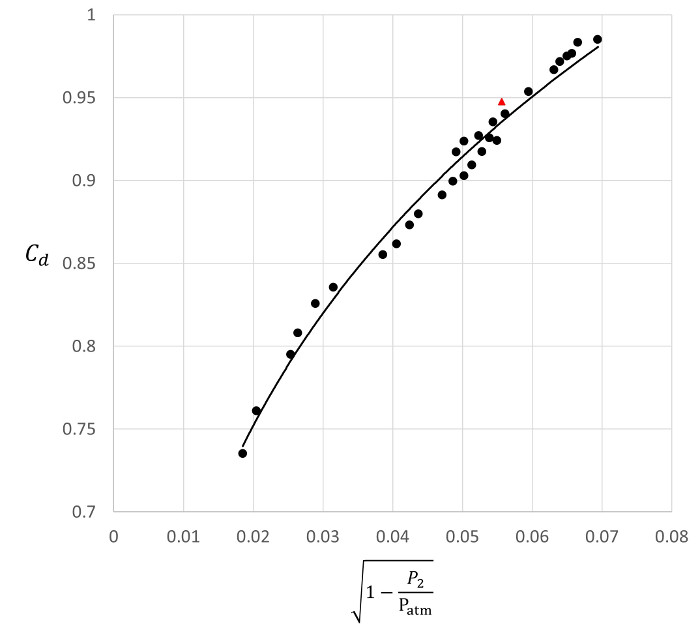
그림 4. 대표적인 결과.  : 다른 유량으로 결정된 배출 계수.
: 다른 유량으로 결정된 배출 계수.  : 본 명세서에서 입증된 속도 측정으로 결정된 방전 계수. - 실험 데이터에 맞는 전력법.
: 본 명세서에서 입증된 속도 측정으로 결정된 방전 계수. - 실험 데이터에 맞는 전력법.
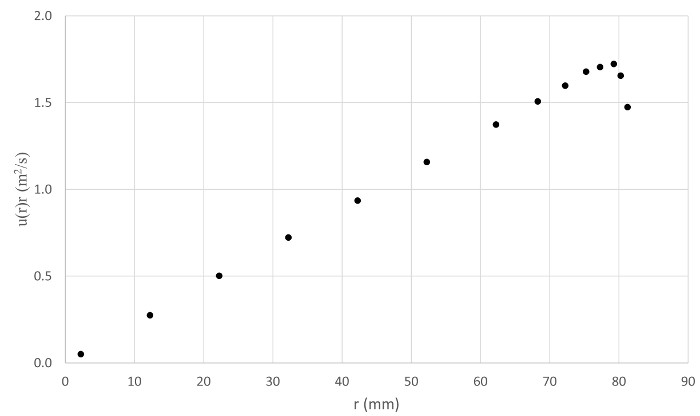
그림 6. 대표적인 결과. 속도와 반지름 사이의 제품 플롯입니다.
표 3. 대표적인 결과. 방전 계수.
| √(1-P2/Patm) | Cd |
| 0.019 | 0.735 |
| 0.020 | 0.761 |
| 0.025 | 0.795 |
| 0.026 | 0.808 |
| 0.029 | 0.826 |
| 0.032 | 0.835 |
| 0.039 | 0.855 |
| 0.041 | 0.862 |
| 0.042 | 0.873 |
| 0.044 | 0.880 |
| 0.047 | 0.891 |
| 0.049 | 0.899 |
| 0.049 | 0.917 |
| 0.050 | 0.924 |
| 0.050 | 0.903 |
| 0.051 | 0.909 |
| 0.052 | 0.927 |
| 0.053 | 0.917 |
| 0.054 | 0.926 |
| 0.054 | 0.935 |
| 0.055 | 0.924 |
| 0.056 | 0.940 |
| 0.060 | 0.953 |
| 0.063 | 0.967 |
| 0.064 | 0.972 |
| 0.065 | 0.975 |
| 0.066 | 0.977 |
| 0.067 | 0.983 |
| 0.069 | 0.985 |
Application and Summary
유동통로를 유량계로 보정하기 위해 질량 보존의 제어 부피 분석의 적용을 입증하였다. 이를 위해 피토 정적 시스템을 사용하여 속도 프로파일에 대한 통합을 사용하여 유동 통로 를 가로질러 유량량을 결정했습니다. 이어서, 방전 계수의 개념은 유동 통로의 벽 근처의 경계층 성장의 효과를 고려하여 통합되었다. 상이한 유량에 대한 속도 측정 세트를 바탕으로, 유동 통로에서 정적 압력과 국소 대기압 사이의 비율의 함수로서 방전 계수를 표현하는 회귀를  개발했다. 마지막으로, 이러한 회귀는 통로를 통과하는 유량에 대한 방정식으로
개발했다. 마지막으로, 이러한 회귀는 통로를 통과하는 유량에 대한 방정식으로  통합되었다. 이 방정식은 로컬 대기 조건, 통로 크기 및 단위 시스템의 변화에 따라 유효성을 유지하기 위해 개발되었습니다.
통합되었다. 이 방정식은 로컬 대기 조건, 통로 크기 및 단위 시스템의 변화에 따라 유효성을 유지하기 위해 개발되었습니다.
질량 보존을 위한 제어 부피 분석은 유동통로를 유량계로 교정하는 많은 대안을 제공합니다. 예를 들어, 천포판, 노즐 및 벤투리 튜브는 통로의 두 개의 서로 다른 섹션 사이의 압력 변화에 따라 유량을 결정하기 위해 제한된 흐름에 사용됩니다. 그리고 우리의 예와 유사하게, 이 장치는 경계 층 효력을 위해 정정하는 방전 계수를 특징으로 할 필요가 있습니다.
개방 채널을 통한 흐름에서 질량 보존을 위한 제어 부피 분석을 사용하여 유출, 부분적으로 열린 게이트 또는 단면 감소와 같은 흐름 제한 전후의 흐름 깊이를 비교하여 유량을 평가할 수도 있습니다. 이러한 응용 프로그램의 주요 의미는 물 분배, 제어 및 처리를 위한 유압 구조는 다른 유동 장치의 사용을 배제하는 매우 큰 스케일이라는 것입니다.
References
- White, F. M. Fluid Mechanics, 7th ed., McGraw-Hill, 2009.
- Munson, B.R., D.F. Young, T.H. Okiishi. Fundamentals of Fluid Mechanics. 5th ed., Wiley, 2006.
- Chapra, S.C. and R.P. Canale. Numerical methods for engineers. Vol. 2. New York: McGraw-Hill, 1998.
- Buckingham, E. Note on contraction coefficients of jets of gas. Journal of Research, 6:765-775, 1931.
- Lienhard V, J.H. and J.H. Lienhard IV. Velocity coefficients for free jets from sharp-edged orifices. ASME Journal of Fluids Engineering, 106:13-17, 1984.
Tags
건너뛰기...
이 컬렉션의 비디오:

Now Playing
질량 보존 및 유속 측정
Mechanical Engineering
22.6K Views

침지된 물체의 부력과 항력
Mechanical Engineering
29.9K Views

플로팅 선박의 안정성
Mechanical Engineering
22.4K Views

추진력과 추력
Mechanical Engineering
21.6K Views

파이프 네트워크 및 압력 손실
Mechanical Engineering
58.0K Views

담금질 및 비등
Mechanical Engineering
7.7K Views

하이드롤릭 점프
Mechanical Engineering
40.9K Views

열교환기 분석
Mechanical Engineering
28.0K Views

냉장 소개
Mechanical Engineering
24.6K Views

열선 풍속 측정
Mechanical Engineering
15.5K Views

난류 측정
Mechanical Engineering
13.5K Views

블러프 바디를 지나는 흐름의 시각화
Mechanical Engineering
11.8K Views

경사 플레이트 대상 제트 충돌
Mechanical Engineering
10.7K Views

시스템 분석에 대한 에너지 보존적 접근 방식
Mechanical Engineering
7.4K Views

제어 볼륨 방법을 사용한 평판 충돌력 결정
Mechanical Engineering
26.0K Views
Copyright © 2025 MyJoVE Corporation. 판권 소유