Théorie de l’orbital moléculaire (OM)

Source : Tamara M. Powers, département de chimie, Texas A & M University

Ce protocole sert de guide dans la synthèse de deux complexes métalliques, mettant en vedette le ligand 1, 1'-bis (diphénylphosphino) ferrocène (dppf) : M (dppf) Cl₂, où M = Ni ou Pd. Alors que les deux de ces complexes de métaux de transition sont 4 coordonnée, ils présentent différentes géométries au centre métallique. En utilisant la théorie des orbitales moléculaires (MO) conjointement avec ¹H RMN et méthode Evans, nous permettra de déterminer la géométrie de ces deux composés.

Il existe une variété de modèles que les chimistes utilisent pour décrire les liaisons dans les molécules. Il est important de se rappeler que les modèles sont des représentations des systèmes et ont donc des points forts mais aussi des limitations importantes. Par exemple, structures de Lewis dot, la méthode la plus simple pour décrire comment les atomes partagent électrons, ne tiennent pas compte de la géométrie des atomes dans la molécule. Théorie de la paire d’électrons de Valence Shell répulsion (VSEPR) décrit la géométrie des atomes, mais elle ne fournit pas une explication pour l’observation que les espèces isoélectroniques avec le même nombre d’électrons de valence peuvent présenter différentes géométries. Surtout pour des complexes de métaux de transition, tous les deux de ces modèles en deçà en décrivant le collage des métaux. Théorie des corps de cristal est un modèle de liaison spécifique à des complexes de métaux de transition. Ce modèle se penche sur les effets du champ électrique du ligand sur les orbitales atomiques d ou f , d’un centre de métal. L’interaction aboutit à un arrêt de la dégénérescence de ces orbitales atomiques.

Dans cette vidéo, nous nous concentrerons sur la théorie OM, qui est un modèle puissant qui peut être utilisé pour décrire les liaisons dans les molécules non seulement groupe principal, mais convient également pour la modélisation des liaisons dans des complexes de métaux de transition. Ici, nous allons démontrer comment générer un diagramme MO métal contenant des composés.

Théorie de l’OM :

Théorie OM décrit une liaison chimique comme la combinaison linéaire des orbitales atomiques (LCAO) de chaque atome dans un composé donné. Les MOs qui résultent de LCAOs décrivent la géométrie et l’énergie des électrons partagés par un nombre d’atomes dans la molécule (c'est-à-dire, la directionnalité et force des liaisons formées par compte tenu des atomes).

Pour revoir les bases de la théorie OM, d’abord examiner la molécule diatomique F₂ (diagramme complet de MO dans la Figure 1). Un atome de fluor a 4 orbitales atomiques de valence : 2s, 2p,_x, 2p_yet 2p_z. L’orbitale 2s est plus faible en énergie que les 2 orbitales atomiquesp , qui tous ont la même énergie. Une combinaison linéaire d’orbitales atomiques se produira entre les orbitales atomiques de l’énergie semblable et de faire correspondre la symétrie. Dans ce cas, l’orbitales 2 sur un atome F interagiront avec les 2s orbital sur l’autre atome de F. L’ajout de ces deux orbitales entraîne la formation d’un σ collage MO (Figure 1). L’attachement est une interaction stabilisante et, par conséquent, la résultante σ MO est plus faible en énergie par rapport à l’énergie des orbitales atomiquess 2. En soustrayant les résultats d’orbitales 2s dans une interaction de anti-liaison (déstabilisation), désigné comme σ *, qui est plus élevé en énergie par rapport aux 2 orbitales atomiquess (Figure 1).

Figure 1. Diagramme de MO de F₂.

De même, les 2 orbitales atomiquesp combinera à forme de liaison et les interactions de anti liaison. Comme les 2 orbitales atomiquess , les 2p_z orbitales atomiques (qui se trouvait le long de la liaison et F) forment des interactions σ et σ *. Si l'on considère les 2p_x et 2p_y orbitales atomiques, nous voyons qu’ils forment des différents types de liaisons et des anti-liaisons interactions, appelés π et π *, respectivement (Figure 1). Il est facile de faire la différence entre σ et π obligations parce que les orbitales de liaisons σ sont cylindrique symétriques autour de l’axe internucléaire, tandis que les orbitales π ont un plan nodal le long de l’axe internucléaire. Le chevauchement spatial entre les orbitales atomiques qui forment des liaisons σ est supérieur à la chevauchement spatial entre les orbitales atomiques qui forment des liaisons π. Par conséquent, la résultante π et π * MOs sont moins stabilisés et déstabilisés, respectivement, par rapport aux MOs σ et σ * formés par les 2 orbitales atomiques de_z p. Nous pouvons ensuite remplir les MOs avec les électrons de valence pour les deux atomes de fluor.

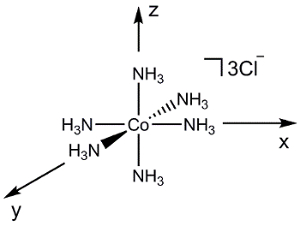
Maintenant, considérons une molécule plus complexe comme [Co (NH₃)₆] Cl₃ (Figure 2). Si nous devions utiliser le même processus que ci-dessus (compte tenu du recouvrement d’orbitales atomique entre 2 atomes à la fois), générer un diagramme de MO de cette molécule serait extrêmement difficile. Au lieu de cela, nous pouvons utiliser la théorie des groupes pour d’abord générer une combinaison linéaire de symétrie adapté (SALC) des ligands. Nous pouvons alors utiliser la symétrie afin de déterminer les interactions collage/anti-bonding qui se forment entre les orbitales atomiques sur le métal et les SALCs qui en résulte.

O ­ h	E	8C3	6C2	6C4	3C2'	J’ai	6S4	8S6	3σh	3σd
Un1 g	1	1	1	1	1	1	1	1	1	1		x2+ y2+ z2
Un2 g	1	1	-1	-1	1	1	-1	1	1	-1
Eg	2	-1	0	0	2	2	0	-1	2	0		(2z2-y2- x2, x2y -2)
T1 g	3	0	-1	1	-1	3	1	0	-1	-1	(R,x, R,y, R,z)
T2 g	3	0	1	-1	-1	3	-1	0	-1	1		(xz, yz, xy)
Un1u	1	1	1	1	1	-1	-1	-1	-1	-1
2u	1	1	-1	-1	1	-1	1	-1	-1	1
Eu	2	-1	0	0	2	-2	0	1	-2	0
T1u	3	0	-1	1	-1	-3	-1	0	1	1	(x, y, z)
T2u	3	0	1	-1	-1	-3	1	0	1	-1
Γ rouge	6	0	0	2	2	0	0	0	4	4

Γ _rouge = A _{1 g} + E _g + T _1U

Figure 2. Combinaison linéaire d’orbitales atomiques ligand [Co (NH₃)₆] Cl₃.

Pour générer le SALCs [Co (NH₃)₆]^{3 +}, nous suivons une procédure semblable, décrite dans la « théorie des groupes » vidéo de la série de Chimie inorganique :

1. Déterminez le groupe ponctuel de la molécule.

2. générer une représentation réductible des orbitales atomiques ligand.

3. réduire la représentation réductible aux représentations irréductibles.

[Co (NH₃)₆] ^{3 +} est le point de groupe O_h. Puisque nous sommes seulement préoccupés par la liaison au centre métallique, on peut simplement considérer les 2 orbitales atomiquess sur chaque ligand de₃ NH. Si nous suivons les étapes 1 à 3 pour le N 2s, orbitales, nous constatons que la représentation réductible est Γ_rouge = un_{1 g} + E_g T_1u (Figure 2). Alors que l’ensemble_{1 g} représente 1 SALC, E,_g et T_1u ensembles représentent en fait SALCs 2 et 3, respectivement, soit un total de 6 SALCs (le même nombre de ligands dans le cation [Co (NH₃)₆]^{3 +}). Les 2 SALCs dans le jeu de_g E ont la même symétrie et seront traduira par MOs dégénérées quand ils interagissent avec les orbitales atomiques de la Co (il peut même sur les 3 SALCs dans le jeu de_1u T). En utilisant le tableau de caractères dans la Figure 2, nous pouvons déterminer comment les orbitales atomiques de Co transforment dans le groupe de point_h O. Par exemple, la d_z² et les orbitales d_{x²– y²} forment un ensemble de_g E. Puisque nous avons 2 SALCs ligand avec une symétrie_g E, ces SALCs seront formera les interactions avec les orbitales atomiques de Co d_x^2-y² d_z² collage/anti-bonding. Continuer de la même façon pour toutes les orbitales atomiques de valence de Co, nous générons un diagramme de MO pour le métaux de transition complexe, illustré à la Figure 3. Notez que le restant d-orbitales (d_xzd_yzet d_xy) transformer comme un ensemble (T_{2 g}), mais n’ont pas une bonne symétrie appariés SALC. Ces orbitales atomiques deviennent donc « non liant » MOs. En d’autres termes, ils ne participent pas en liaison avec les ligands dans ce complexe de métaux de transition.

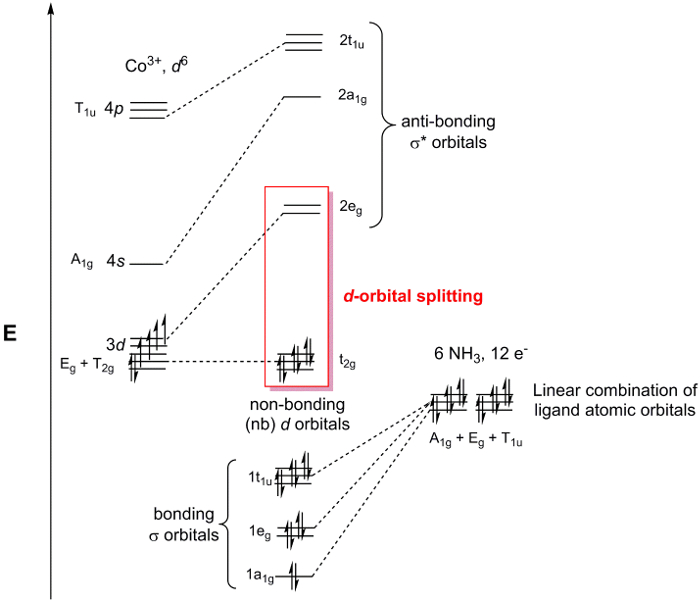
Figure 3. Diagramme de MO pour [Co (NH₃)₆] Cl₃.

Mis en évidence dans la Figure 3 sont les non-liantes d-orbitales et les orbitales σ * avec d-caractère orbitale. Lorsque ce groupe de MOs est dissociée de l’ensemble du diagramme MO il est dénommé le d-orbitale fractionnement diagramme d’un métal de transition complexes. Depuis le d-orbitale fractionnement diagramme contient l’HOMO et la LUMO, qui sont généralement les orbitales plus importants pour comprendre la chimie et la spectroscopie des complexes de coordination, chimistes fera souvent référence à la d-orbital fractionnement de diagramme au lieu de l’ensemble du diagramme MO. Idéalement, le d-orbitale schéma de fractionnement peut être rempli avec le nombre de de^– sur le centre métallique, puisque les électrons axée sur le ligand toujours remplissent les MOs σ-basé dans le diagramme de MO.

Compte tenu de la d -diagrammes de fractionnement orbitale pour M() dppf) Cl₂:

Envisager une simple 4-coordonnées métallique complexe MX₄. MX₄ peut exister sous deux géométries : tétraédrique ou plan carré. Le d-orbitales fractionnement des diagrammes pour le point rassemble les T_d (tétraédrique) et D_{4 h} (plan carré) est illustré à la Figure 4. Alors que les complexes métalliques générales M (dppf) Cl₂ n’ont pas 4 ligands équivalents et ne sont donc pas dans le point groupes T_d ou D_{4 h}, nous pouvons toujours utiliser ces d-orbitale fractionnement des diagrammes comme un modèle pour décrire le d -MOs orbitales pour les deux géométries possibles.

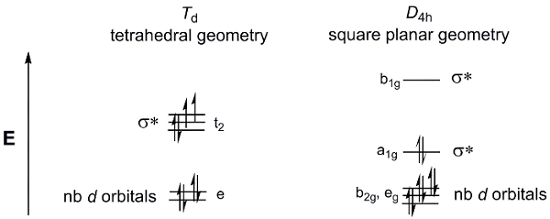
Figure 4. Le d-orbitale diagrammes pour le point de séparation des groupes T_d (tétraédrique) et D_{4 h} (plan carré).

Maintenant, considérons le d-nombre d’électrons pour M (dppf) Cl₂. Ni tant de Pd sont dans le groupe 10 du tableau périodique. Par conséquent, les deux auront le même état d’oxydation (2 +) et d-nombre d’électrons (m⁸). Si nous remplissons les deux d-orbitales fendage diagrammes ci-dessus avec 8 électrons, nous voyons que la géométrie plane carré aboutit à un complexe diamagnétique, alors que le diagramme de MO tétraédrique est conforme à une espèce paramagnétique. Il y a plusieurs facteurs qui entrent dans la détermination dont la géométrie est favorisée énergétiquement. Dans la géométrie du plane carré, il y a moins d’électrons dans les orbitales anti-collage, ce qui indiqueraient que la géométrie plane carré est plus électroniquement favorisée. Cependant, nous devons aussi considérer l’énergie requise pour la paire d’électrons. L’électron appariement d’énergie dans les molécules de plans carré est plus élevé que dans les molécules tétraédriques, qui ont moins orbitales complètement remplis. Enfin, il faut examiner le montant le σ * d-orbitales sont déstabilisés. Plus gros atomes métalliques ont une plus grande chevauchement spatial avec des ligands, résultant en plus énergie σ * d-orbitales.

Enfin, nous devons aussi considérer l’apport d’énergie de répulsions stériques. La géométrie tétraédrique est plus stériquement favorisé (avec des angles de 109,5 °) par rapport à la géométrie plane carré (90 °). Par conséquent, il y a plusieurs facteurs défavorables qui affectent dont la géométrie est plus favorable, étant donné l’identité de M dans M (dppf) Cl₂.

Nous serons en mesure de faire la distinction entre ces deux géométries à l’aide de NMR. Si la molécule est un plane carré, nous observerons un retard diagnostique ¹H d’unespèces diamagnétiques. Si la molécule est tétraédrique, nous remarquerons signaux paramagnétiques en ¹H RMN. Enfin, nous allons utiliser la méthode Evans (voir la vidéo de «Méthode Evans» pour plus de détails) afin de déterminer le moment magnétique de solution des espèces paramagnétiques.

Remarque : Pour les mesures de sécurité, la sécurité de ligne Schlenk devrait être revue avant d’effectuer les expériences. Verrerie doit être inspecté pour fissures star avant d’utiliser. Il faut pour s’assurer que O₂ n’est pas condensée dans le piège de ligne Schlenk si vous utilisez le liquide N₂. À température₂ N, O₂ se condense et est explosif en présence de solvants organiques. Si l'on soupçonne que O₂ a été condensée ou un liquide bleu est observé dans le piège froid, laissez le piège froid sous vide dynamique. Ne pas enlever le liquide N₂ collecteur ou éteignez la pompe à vide. Au fil du temps le liquide O₂ va s’évaporer dans la pompe ; Il est sécuritaire d’enlever le piège de₂ N liquid une fois tous les O₂ s’est évaporée. Pour plus d’informations, voir la vidéo de « Synthèse d’une ligne de TI métallocène Using Schlenk Technique ». ¹

1. installation de la ligne de Schlenk pour la synthèse de Ni (dppf) Cl₂ et Pd (dppf) Cl₂

Remarque : Pour une procédure plus détaillée, veuillez consulter la vidéo de « Schlenk lignes transfert de solvant » dans la série Essentials of Organic Chemistry ).

1. Fermez le robinet de purge.
2. Allumez le gaz₂ N et la pompe à vide.
3. Comme le Schlenk ligne vide atteint sa pression minimale, préparer le piège froid avec liquide N₂ ou neige carbonique et d’acétone.
4. Assembler le piège froid.

2. synthèse de la NC (dppf) Cl₂ (Figure 5) dans des Conditions d’anaérobie/inerte

Remarque Bien que la synthèse de la NC (dppf) Cl₂ peut être effectuée dans des conditions aérobies, des rendements plus élevés sont obtenus lorsque mené dans des conditions anaérobies.

1. Ajouter dppf 550 mg (1 mmol) et 40 mL d’isopropanol dans une fiole de trois-cou.
   Remarque dppf peut être acheté chez Sigma Aldrich ou synthétisés à l’aide de méthodes trouvées dans la littérature. ²
2. Monter le cou Centre du ballon à trois-cou avec un condenseur et un adaptateur d’aspiration. Monter deux cous restants avec bouchon 1 verre et 1 septum en caoutchouc.
3. Dégazer la solution par propagation N₂ gaz, par le solvant pendant 15 min. utilisation l’adaptateur sous vide au dessus du condensateur comme le « vent ».
4. Branchez l’adaptateur vide dans la partie supérieure du condenseur N₂ à l’aide de la ligne de Schlenk.
5. Commencer à chauffer le ballon trois-cou dans un bain d’eau réglé à 90 ° C.
6. Une seule cou ballon à fond rond, ajouter 237 mg NiCl₂·6H₂O(1 mmol) de 4 mL d’un mélange de 2:1 d’isopropanol (réactif) et de méthanol (réactif). Laisser agir le mélange jusqu'à ce que tout le sel Ni a dissous (environ 1 min).
   Remarque : Si un sonicateur n’est pas disponible, chauffer doucement le mélange dans un bain-marie.
7. Dégazer la solution Ni par propagation N₂ gaz dans le mélange pendant 5 min.
8. Ajouter la NiCl₂·6H₂O solution dans le ballon fond rond col trois via transfert de canule.
9. Permettre la réaction au reflux pendant 2 h à 90 ° C.
10. Permettre la réaction refroidir dans un bain de glace. Isoler le précipité vert obtenu par filtration sous vide dans un entonnoir fritté.
11. Lavez le produit avec 10 mL d’isopropanol froid, suivie de 10 mL d’hexane.
12. Laisser le produit à l’air sec avant la préparation de l’échantillon de NMR.
13. Prendre une ¹H RMN du produit dans le chloroforme -d.
14. Si le ¹H RMN est indicative d’une espèce paramagnétique, préparer un NMR pour la méthode Evans, en suivant les instructions à l’étape 4.

Figure 5. Synthèse de la NC (dppf) Cl₂.

3. synthèse du Pd (dppf) Cl₂ (Figure 6)¹

Remarque : Utiliser des techniques de ligne Schlenk standard pour la synthèse de Pd (dppf) Cl₂ (voir la vidéo de « Synthèse d’une ligne de TI métallocène Using Schlenk Technique »).

Remarque Bien que la synthèse du Pd (dppf) Cl₂ peut être effectuée dans des conditions aérobies, des rendements plus élevés sont obtenus lorsque mené dans des conditions anaérobies.

1. Ajouter dppf 550 mg (1 mmol) et 383 mg (1 mmol) de chlorure de bis(benzonitrile)palladium(II) dans un ballon de Schlenk et préparer le ballon de Schlenk le transfert de la canule de solvant.
2. Ajouter 20 mL de toluène dégazée dans le ballon de Schlenk via transfert de canule.
3. Permettre la réaction de remuer pendant au moins 12 h à température ambiante.
4. Isoler le précipité orange obtenu par filtration sous vide dans un entonnoir fritté.
5. Lavez le produit au toluène (10 mL), suivi des hexanes (10 mL).
6. Laisser le produit à l’air sec avant la préparation de l’échantillon de NMR.
7. Prendre une ¹H RMN du produit dans le chloroforme -d.
8. Si le ¹H RMN est indicative d’une espèce paramagnétique, préparer un NMR pour la méthode Evans, suivant les instructions décrites à l’étape 4.

La figure 6. Synthèse du Pd (dppf) Cl₂.

4. préparation de l’échantillon de méthode Evans

Remarque : Pour une procédure plus détaillée, veuillez consulter la vidéo de « Méthode Evans ».

1. Dans un flacon à scintillation, préparer une solution de 50 : 1 (volume : volume) du chloroforme -d: trifluorotoluène. Pipette de 2 mL de solvant deutéré et à cela ajouter 40 µL de trifluorotoluène. Boucher le flacon.
   Remarque : Dans cet exemple, nous utiliserons ¹⁹F RMN à observer le décalage du signal F dans trifluorotoluène en présence de l’espèce paramagnétique.
2. Grâce à cette solution, préparer l’insert capillaire.
3. Peser 10 à 15 mg de l’échantillon paramagnétique dans un nouveau flacon à scintillation et noter la masse.
4. Pipette ~ 600 µL du mélange solvant préparé dans le flacon contenant les espèces paramagnétiques. Noter la masse. Assurez-vous que le solide se dissout complètement.
5. Dans un tube standard de NMR, soigneusement déposer l’insert capillaire à un angle, pour s’en assurer qu'il ne rompt pas.
6. Distribuer la solution contenant l’espèce paramagnétique dans le tube de NMR.
7. Acquérir et conserver un spectre de RMN F standard ¹⁹.
8. Noter la température de la sonde.
9. Notez la radiofréquence.

Pd (dppf) Cl₂:
¹ H RMN (chloroforme -d, 400 MHz, δ, ppm) : 4.22 (alpha-H), 4,42 (bêta-H), 7,89 7.44, 7,54 (aromatiques)³.

Ni (dppf) Cl_2 :
¹ H RMN (chloroforme -d, 300 MHz, δ, ppm) : 20,85 10.04, 4.23, 3,98, 1.52,-3.31,-7.10.
Méthode d’Evans, regardant la MAJ ¹⁹F de trifluorotoluène :

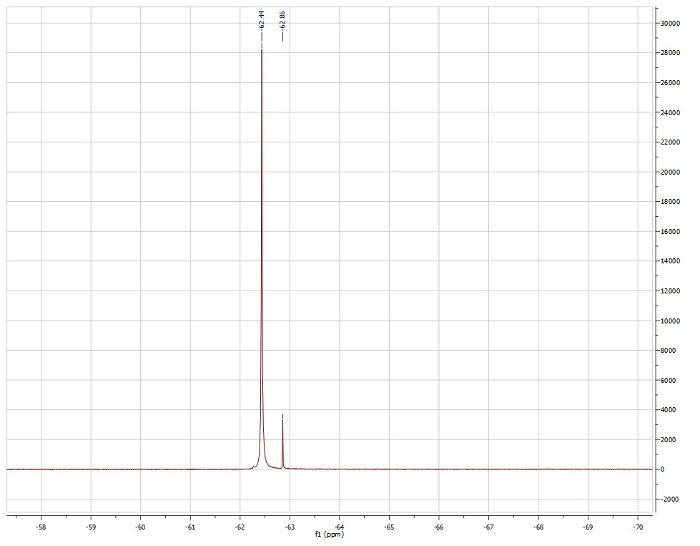
Observéµ_eff = 3,15 µ_b
Masse de l’échantillon : 9,5 mg
Masse de la solution (chloroforme -d + trifluorotoluène) : 0,8365 g
Température de sonde : 296,3 K
RMN du champ (MHz) : 470.06
Signalé µ_eff = 3.39 µ_b. ⁴
Pour S = 1 (prédite basée sur une géométrie tétraédrique, Figure 4), µ théorique_eff = 2,83 µ_b.
S = 3/2, µ théorique_eff = 3,46 µ_b.

Basé sur les ¹H RMN, nous voyons que les Pd (dppf) Cl₂ est diamagnétique et présente donc une géométrie plane carré. Le ¹H RMN de Ni (dppf) Cl₂ est paramagnétique et par conséquent est tétraédrique au centre Ni. Méthode d’Evan confirme que Ni (dppf) Cl₂ est paramagnétique, présentant un solution du moment magnétique de 3,15 µ_b, qui est proche de la littérature des rapports des valeurs pour ce composé. Puisque Ni est petit, le sterics l’emporte sur toute stabilisation électronique associée à la géométrie plane carré, faisant Ni (dppf) Cl₂ tétraédrique. En revanche, le Pd est grande et, donc, a plus énergie σ * d-orbitales. Dans ce cas, la stabilisation électronique l’emporte de beaucoup sur les répulsions stériques, résultant en une géométrie plane carré à Pd à Pd (dppf) Cl₂.

Cette vidéo démontre comment la théorie OM peut être utilisée comme un modèle de la liaison de complexes de métaux de transition. Nous avons synthétisé deux complexes avec la formule générale M (dppf) Cl₂. Lorsque M = Ni, les pièces complexes 4 coordonnée une géométrie tétraédrique. Remplacement de l’atome Ni avec un métal de transition plus grand (pp), la molécule prend géométrie plane carré.

Auparavant, nous avons appris sur le rôle important que joue le ferrocène dans le domaine de la chimie organométallique. Ferrocènes substitués, y compris dppf, sont utilisées comme ligands pour 1^st, 2^èmeet 3^rd row les métaux de transition chélatants. Les complexes qui en résultent sont utilisées dans la catalyse homogène (i.e., [dichlorure de 1,1'-bis(diphenylphosphino)ferrocene]palladium(II), Pd (dppf) Cl₂, est un catalyseur pour les réactions de formation de la liaison C-C et C-hétéroatome).

Il est important pour expliquer leur structure et la réactivité de comprendre la liaison dans les complexes de métaux de transition. Un des points forts de la théorie OM est qu’elle fournit un bon modèle qui peut servir à expliquer la réactivité des complexes de métaux de transition. Dans de nombreux cas, le centre métallique est l’emplacement de toute réactivité manifestée par la molécule. Par conséquent, il est utile d’avoir une image de la densité électronique au centre métallique, qui est résumé dans le d -fendage diagramme d’orbitales dérivé de la théorie OM (Figure 3). Notez que non seulement faire les MOs dans le d-diagramme d’orbitales fendage présentent pour la plupart d-caractère orbitale (les orbitales σ * sont les plus proches en énergie de l' atome d-orbitales du métal et donc la plus grande partie de la densité électronique dans ces MOs est centré sur l’atome de métal), mais aussi le schéma de fractionnement contient l’HOMO et LUMO de la molécule. Par conséquent, toute chimie qui se produit affectera directement les d-orbitale fractionnement diagramme de la molécule.