JoVE Science Education
Physics II
Hai accesso completo a questo contenuto tramite
Nanyang Technological UniversityOnde sonore e effetto Doppler
Panoramica
Fonte: Arianna Brown, Asantha Cooray, PhD, Dipartimento di Fisica e Astronomia, Scuola di Scienze Fisiche, Università della California, Irvine, CA
Le onde sono disturbi che si propagano attraverso un mezzo materiale o uno spazio vuoto. Le onde luminose possono viaggiare attraverso un vuoto e alcune forme di materia, e sono trasversali in natura, il che significa che le oscillazioni sono perpendicolari alla direzione di propagazione. Tuttavia, le onde sonore sono onde di pressione che viaggiano attraverso un mezzo elastico come l'aria e sono di natura longitudinale, il che significa che le oscillazioni sono parallele alla direzione di propagazione. Quando il suono viene introdotto in un mezzo da un oggetto vibrante, come le corde vocali di una persona o le corde in un pianoforte, le particelle nell'aria sperimentano un movimento avanti e indietro mentre l'oggetto vibrante si muove avanti e indietro. Ciò si traduce in regioni nell'aria in cui le particelle d'aria sono compresse insieme, chiamate compressioni, e altre regioni in cui sono distribuite, chiamate rarefazioni. L'energia creata da un'onda sonora oscilla tra l'energia potenziale creata dalle compressioni e l'energia cinetica dei piccoli movimenti e velocità delle particelle del mezzo.
Compressioni e rarefazioni possono essere utilizzate per definire la relazione tra velocità e frequenza delle onde sonore. L'obiettivo di questo esperimento è misurare la velocità del suono nell'aria ed esplorare l'apparente cambiamento di frequenza per un oggetto che emette onde sonore mentre è in movimento, chiamato effetto Doppler.
Principi
Quando un'onda sonora si propaga, periodicamente comprime e rarefica (si diffonde) le molecole d'aria in qualsiasi posizione. Poiché la relazione tra pressione e densità dipende dalla temperatura, la velocità del suono che viaggia attraverso l'aria dipende anche dalla temperatura e definita come:
 (Equazione 1)
(Equazione 1)
dove TC è la temperatura dell'aria in gradi Celsius (°C) e v è la velocità dell'onda sonora misurata in metri al secondo (m/s). Classicamente, la velocità di un'onda è definita come:
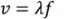 (Equazione 2)
(Equazione 2)
dove λ è la lunghezza d'onda (m), o la distanza tra le onde di pressione, e f è la frequenza (Hz), o il numero di onde per unità di tempo. L'equazione 1 è una stima per l'aria che è ferma; se il mezzo dell'onda sonora è in viaggio, la velocità del suono cambierà a seconda della direzione del movimento. Ad esempio, le onde sonore che si muovono opposte in direzione di forti venti avranno probabilmente la loro velocità diminuita dalla velocità del vento. In questo esperimento, questo effetto è trascurabile.
Quando la sorgente del suono sta cambiando velocità o direzione e il mezzo è generalmente fermo, non vi è alcun cambiamento nella velocità dell'onda sonora. Tuttavia, un osservatore può sentire un falso aumento o diminuzione della frequenza a causa dell'effetto Doppler. Man mano che la sorgente delle onde si avvicina all'osservatore, le onde vengono emesse in posizioni più vicine tra loro. Sono ancora emessi alla stessa frequenza, ma a causa delle loro posizioni relative mentre la sorgente si muove raggiungono l'osservatore raggruppato insieme e apparentemente a una frequenza più elevata. Con la stessa logica, quando la sorgente si allontana dall'osservatore, l'osservatore sente il suono a frequenze più basse. Il modo più semplice per capire questo effetto è immaginare un'auto della polizia con una sirena che guida verso un pedone: mentre guida verso il pedone, la frequenza al pedone sembra salire sempre di più fino a quando finalmente l'auto supera il pedone, e il pedone inizia a sentire frequenze che diminuiscono man mano che l'auto si allontana. La relazione tra la frequenza osservata f e la frequenza emessa f0 èdefinita da:

dove c è la velocità delle onde sonore nell'aria, vr è la velocità del ricevitore rispetto al mezzo e (= 0 se il ricevitore è a riposo), e vs è la velocità della sorgente rispetto al mezzo.
In questo esperimento, calcoleremo la velocità del suono usando varie frequenze e lunghezze d'onda e confronteremo tale velocità con la velocità teorica. Osserveremo anche l'effetto Doppler sulle frequenze emesse da un diapason.
Procedura
1. Misurare la velocità del suono
- Set up: due altoparlanti uno di fronte all'altro su un banco ottico. Un altoparlante deve essere collegato a un generatore di funzioni (segnale) su un lato di un tee BNC, con l'altro lato del tee BNC collegato al canale A sull'oscilloscopio. Il secondo altoparlante deve essere collegato al canale B dell'oscilloscopio.
- Accendere il generatore di segnale e l'oscilloscopio e regolare la manopola sul generatore per produrre un'onda di 5 kHz. L'altoparlante collegato al generatore di funzioni dovrebbe produrre un tono costante che suona come un allarme e due onde dovrebbero apparire sull'oscilloscopio.
- Far scorrere l'altoparlante collegato al canale B lungo la panca fino a quando le due onde non sono in fase. Registrare la distanza tra i due altoparlanti.
- Far scorrere lentamente l'altoparlante del canale B all'indietro in modo che le onde siano fuori fase. Continua a scivolare all'indietro fino a quando le onde non sono di nuovo in fase. Registrare la nuova distanza tra gli altoparlanti.
- Sottrarre la distanza finale dall'iniziale per trovare la lunghezza d'onda del suono. Utilizzare questo valore e la frequenza per calcolare la velocità osservata del suono utilizzando l'equazione 2.
- Ripetere i passaggi 1,3-1,5 per le frequenze 8 kHz e 3 kHz. Si noti la relazione inversamente proporzionale tra lunghezza d'onda e frequenza.
- Confronta le velocità sperimentali con la velocità prevista utilizzando la temperatura dell'aula.
2. Effetto Doppler con un diapason / apparato Doppler
Il video mostra un esperimento che utilizza un apparato Doppler, ma questo stesso esperimento potrebbe essere effettuato utilizzando un diapason. Il protocollo che utilizza un diapason è descritto qui:
- Legare un pezzo di corda lungo 1 m all'estremità di un diapason. Se tenuto alla lunghezza della vita, il diapason dovrebbe avvicinarsi ma non toccare il pavimento.
- Collegare un microfono a un canale oscilloscopio e posizionare il microfono a una distanza fissa (circa 1,5 m).
- Premi il diapason per creare un suono e tieni premuto in posizione a 1,5 m dal microfono. Notate quante onde appaiono sullo schermo.
- Premi di nuovo il diapason e inizia a far oscillare la forcella in cerchio a velocità costante.
- Coloro che osservano il diapason oscillante noteranno che quando la forcella oscilla verso di loro, la frequenza, o il tono, diventa più alta. Allo stesso tempo, l'oscilloscopio dovrebbe mostrare leggermente più onde sullo schermo. Mentre si allontana da loro, il tono si abbassa e l'oscilloscopio dovrebbe mostrare un po 'meno onde sullo schermo. Vedere la Figura 1 di seguito per un esempio di visualizzazione dell'oscilloscopio.
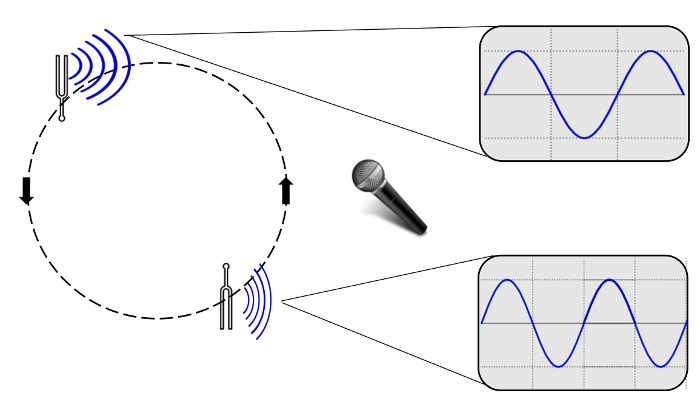
Figura 1: Rappresentazione delle onde sonore di un diapason sottoposte all'effetto Doppler catturate da un oscilloscopio. Mentre la forcella oscilla verso il microfono, le onde sonore vengono emesse a distanze più ravvicinate e creano l'illusione di un tono più alto. Nota: la variazione di frequenza delle onde tracciate sul monitor dell'oscilloscopio può essere sottile e l'ampiezza delle onde cambierà anche rispetto alla posizione del diapason poiché l'ampiezza dell'onda sonora è proporzionale al volume (o "volume").
Risultati
Temperatura ambiente: 20 °C
Velocità prevista: v = 331,4 + 0,6(20) = 343,4 m/s
| Frequenza | Distanza iniziale in fase | Distanza finale in fase | Lunghezza d’onda | Velocità calcolata | Errore % |
| 5 kHz | 27,4 cm | 34,3 cm | 6,90 cm | 345 m/s | 0.5% |
| 8 kHz | 25,5 cm | 29,75 cm | 4,25 cm | 340 m/s | 1.0% |
| 3 kHz | 22,8 cm | 34,2 cm | 11,40 cm | 342 m/s | 0.4% |
Usando l'equazione 2, la velocità del suono può essere calcolata su un valore abbastanza accurato. Ad esempio, per la prima frequenza, f = 5 kHz = 5.000 Hz e λ = 6,90 cm = 0,069 m, quindi velocità = λf = 5.000 x 0,069 = 345 m/s. Per determinare l'errore tra la velocità prevista e la velocità osservata, utilizziamo quanto segue:
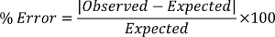
L'effetto Doppler sarà evidente dall'oscillazione del diapason o da qualsiasi altro oggetto che emette suoni. Mentre il diapason oscilla verso il microfono, le onde sonore si raggruppano producendo una frequenza più alta, come evidente dal raggruppamento di onde sonore sull'oscilloscopio. Man mano che la forcella si allontana, le onde diventano più diffuse e così fanno le onde sull'oscilloscopio.
Applicazione e Riepilogo
In questo esperimento, le proprietà ondulate del suono sono definite ed esplorate. In particolare, è stata confermata la relazione tra frequenza delle onde sonore, lunghezza d'onda e velocità. I diapason sono progettati per emettere una sola frequenza, rendendoli dispositivi ottimali per dimostrare l'effetto Doppler. Man mano che il diapason si avvicina sempre più lontano dall'osservatore, la frequenza appare rispettivamente più alta e più bassa. Sia l'effetto Doppler che l'equazione 2 possono essere estesi ad altre forme di onde, come la luce.
Come esseri umani, usiamo le onde sonore per comunicare ogni giorno. Tuttavia, una di queste forme di comunicazione rappresenta veramente il modo in cui la nostra specie ha sfruttato per la prima volta la fisica del suono: la musica, in particolare gli strumenti che richiedono respiro. Gli strumenti a colonna d'aria aperta, come la tromba, la tuba o il flauto, sono costituiti da una colonna d'aria racchiusa all'interno di un tubo cavo che a volte è curvo. Quando l'aria viene spinta nello strumento, si verifica una vibrazione all'interno che fa sì che le onde di pressione si riflettano all'interno del tubo. Tuttavia, solo le onde di pressione di determinate lunghezze d'onda e frequenze si riflettono in modo tale da iniziare a interferire con le onde incidenti creando così onde di pressione stazionarie. Ogni strumento musicale ha un insieme di frequenze naturali a cui vibra o risuona. Queste sono chiamate armoniche e ogni armonica è associata a uno specifico modello di onda stazionaria definito dai suoi punti finali, lunghezza d'onda e frequenza. In un flauto, i fori possono essere aperti lungo il flauto per ridurre la lunghezza effettiva dei confini, riducendo così la lunghezza d'onda e aumentando la frequenza. In una tromba, le valvole fanno viaggiare l'aria attraverso diverse parti della tromba che sono di dimensioni diverse, con conseguenti cambiamenti di lunghezza d'onda e frequenza.
Una notevole applicazione dell'effetto Doppler è il radar Doppler, utilizzato dai meteorologi per leggere gli eventi meteorologici. In genere, un trasmettitore emette onde radio a una frequenza specifica verso il cielo da una stazione meteorologica. Le onde radio rimbalzano dalle nuvole e dalle precipitazioni e poi tornano alla stazione meteorologica. La frequenza delle onde riflesse verso la stazione sembra diminuire se le nuvole o le precipitazioni si allontanano dalla stazione, mentre la frequenza radio sembra aumentare se gli oggetti atmosferici si muovono verso la stazione. Questa tecnologia può anche essere applicata per determinare la velocità e la direzione del vento.
L'effetto Doppler ha anche applicazioni nella fisica medica. In un ecocardiogramma Doppler, le onde sonore di una certa frequenza vengono incanalato nel cuore e si riflettono sulle cellule del sangue che si muovono attraverso il cuore e i vasi sanguigni. Simile al radar Doppler, i cardiologi possono capire la velocità e la direzione del flusso sanguigno nel cuore a causa dello spostamento delle frequenze ricevute dopo la riflessione. Questo può aiutarli a identificare le aree di ostruzione nel cuore.
Vai a...
Video da questa raccolta:

Now Playing
Onde sonore e effetto Doppler
Physics II
23.5K Visualizzazioni

Campi elettrici
Physics II
77.6K Visualizzazioni

Potenziale elettrico
Physics II
105.1K Visualizzazioni

Campi magnetici
Physics II
33.6K Visualizzazioni

Carica elettrica in un campo magnetico
Physics II
33.7K Visualizzazioni

Leggi di Ohm per conduttori ohmici e non ohmici
Physics II
26.3K Visualizzazioni

Resistori in serie e in parallelo
Physics II
33.2K Visualizzazioni

Capacità
Physics II
43.8K Visualizzazioni

Induttanza
Physics II
21.6K Visualizzazioni

Circuiti elettrici RC/RL/LC
Physics II
143.0K Visualizzazioni

Semiconduttori
Physics II
29.9K Visualizzazioni

Effetto fotoelettrico
Physics II
32.7K Visualizzazioni

Riflessione e rifrazione
Physics II
36.2K Visualizzazioni

Interferenza e diffrazione
Physics II
91.3K Visualizzazioni

Onde stazionarie
Physics II
49.9K Visualizzazioni
Copyright © 2025 MyJoVE Corporation. Tutti i diritti riservati
Utilizziamo i cookies per migliorare la tua esperienza sul nostro sito web.
Continuando a utilizzare il nostro sito web o cliccando “Continua”, accetti l'utilizzo dei cookies.