Capacitancia

Fuente: Yong P. Chen, PhD, Departamento de física & Astronomía, Facultad de Ciencias, Universidad de Purdue, West Lafayette, IN

Este experimento utilizará condensadores comerciales y un condensador de placas paralelas para demostrar el concepto de capacitancia. Un condensador almacena enfrente cargos de dos conductores, por ejemplo dos opuestos placas del metal, llevando a una diferencia de potencial (tensión) entre los dos conductores. La cantidad de carga en cada conductor es proporcional a esta caída de tensión, con la capacitancia como el factor de proporcionalidad. Si la tensión está cambiando con el tiempo, la corriente que fluye en el condensador será proporcional a la tasa de cambio, y de nuevo la capacitancia es el factor de proporcionalidad.

La capacitancia del capacitor de placas paralelas es el producto de la constante dieléctrica con la distancia entre las placas dividida por el área de la placa. Este experimento demostrará la proporcionalidad con la distancia primero depositar algo de carga en el condensador y luego utilizando un voltímetro de alta impedancia (Electrómetro) para monitorear la tensión entre las placas como se aumenta la distancia. El cambio de tensión también será monitoreado con un material dieléctrico, tal como una placa de plástico insertado en el espacio entre las placas de metal.

Se utilizará un medidor de capacitancia directamente medir la capacitancia, así como a las medida paralelo y conexiones en serie de condensadores disponibles comercialmente y para estudiar cómo la capacitancia total se relaciona con capacitancias individuales.

Un condensador consiste en dos conductores separados y su capacitancia C representa su "capacidad para almacenar carga". Aplicando una diferencia de voltaje V entre estos dos conductores puede inducir la carga + Q en un conductor y Q en el otro conductor (así que la carga total es cero, es decir, el condensador como un todo es carga neutra), tal que:

(Ecuación 1)

Nota aquí que Q es la carga en un conductor (no la carga total en ambos conductores que sería 0). Si el voltaje V está cambiando con el tiempo, también lo hará la carga Q. Si V y Q cambian por ΔV y ΔQ, respectivamente, en un Δt de intervalo de tiempo, entonces,

ΔQ = C • ΔV

y

Desde ΔQ/Δt es la corriente (denominada "corriente de carga") que fluye en el conductor cargado positivamente del condensador, entonces como se muestra en la ecuación 2:

(Ecuación 2)

Esto significa que la capacitancia es el factor de proporcionalidad para convertir la tasa de cambio de voltaje (ΔV/Δt) a la corriente que fluye en el condensador (ver figura 1).

La capacitancia puede ser medida directamente con un medidor de capacitancia (por ejemplo, el modo de medición de la capacitancia de un multímetro o "Medidor de LCR"; véase la figura 2).

El tipo más simple de capacitor, representado en las figuras 1 y 2, consiste en dos placas conductoras paralelas y se llama un "condensador de placas paralelas". Su capacitancia C es dado por la ecuación 3

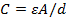(Ecuación 3)

donde A es el área de la placa, d es la separación entre las placas y es la constante dieléctrica del medio entre las dos placas (o "llenar" el condensador). El medio debe ser eléctricamente aislantes. Para un vacío,

F/m

Este valor se denota comúnmente como ε₀, que también describe ε de aire para una buena aproximación. Otro medio, como el petróleo, tienen generalmente un más grande ε, que se ajusta desde el valor del vacío ε₀ citado arriba por un factor mayor que uno. Este factor es conocido como el "relativo" constante dieléctrica o permitividad del medio y comúnmente denotado como κ. Tal medio se denomina también generalmente un material"dieléctrico".

Por lo tanto, para un condensador de placas paralelas:

Si la carga Q es fija, entonces aumentando la placa placa separación d aumentará el voltaje V (proporcional a d):

(Ecuación 4)

Los condensadores pueden conectarse en paralelo o en serie como resistencias. La capacitancia total «efectiva» es relacionado a las capacitancias en una conexión paralelo o serie similar conductancia eléctrica como de una serie/paralelo conexión resistencia conductancias individuales relacionados con. Así, para dos capacitores con capacitancias C₁ y C₂, el capacitancia total para una conexión en paralelo es igual a la suma de las dos capacitancias. O,

(Ecuación 5)

Para una conexión en serie,

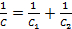(Ecuación 6)

Estos dos tipos de conexiones se muestran en las figuras 3 y 4.

Figura 1: Diagrama que muestra un condensador conectado a una fuente de voltaje utilizada para cargar el condensador y un amperímetro para leer la corriente.

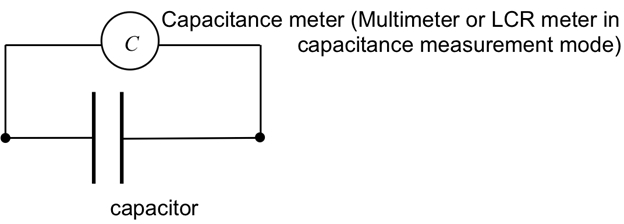
Figura 2: Diagrama que muestra un medidor de capacitancia conectado a un condensador para medir directamente su capacitancia.

1. carga de un condensador

1. Obtener un condensador comercial con una capacitancia C = 470 μF (o algún valor similar), una fuente de voltaje programable y un amperímetro (o multímetro puede medir actual).
2. Con la fuente de tensión a 0 V, conecte el terminal "+" de la fuente de tensión a un terminal del condensador, con el amperímetro en el medio y conecte el terminal "−" de la fuente de voltaje a la terminal, como en la figura 1. La conexión puede realizarse con cables con pinzas o enchufes de plátano en recepción de puertos en el condensador e instrumentos.
3. Cambiar la fuente de tensión de 0 V a 1 V (de aproximadamente 1 s), y observar el transitorio actual de lectura en el amperímetro. Hacer lo mismo con 2 V, 5 V y 10 V (para cada voltaje objetivo; esto significa que primero ir a 0 V, luego cambiar a la tensión de destino en alrededor de 1 s). Tenga en cuenta que la corriente transitoria es más grande para una mayor tensión de objetivo, como se esperaba de ecuación 2.
4. Programa de la fuente de voltaje para generar una rampa de tensión de 0 V a 10 V en 5 s y grabar la lectura de "estado estacionario" de la metro del amperio durante la mitad de la rampa. Repita para un tiempo de rampa de 10 s, 20 s y 30 s. parcela la corriente observada versus la tasa de rampa de tensión (en V/s).

2. Ajuste de la capacitancia

1. Apague la fuente de voltaje y reemplazarla con una batería de V 300 y vuelva a colocar el amperímetro una resistencia MΩ 1 (el propósito de este resistor es proporcionar protección adicional para limitar la corriente en el circuito); también Reemplace el condensador comercial con un condensador de placas paralelas con una separación ajustable entre las placas.
2. Obtener un voltímetro de alta impedancia (o "Electrómetro") y conectarlo para medir la diferencia del voltaje V entre las dos placas (la impedancia alta impide la descarga del condensador durante el experimento cuando se conecta el electrómetro). Vea la figura 5.
3. Conectar la batería de V 300 para el condensador de placas paralelas, espere hasta que el electrómetro alcanza el estado estacionario de 300 V (ahora el condensador está cargado por la fuente V 300) y entonces desconectar rápidamente la fuente de tensión de las placas. Vea la figura 6. El electrómetro todavía deberá leer 300 V.
4. Ahora aumentar la distancia d entre las placas más grandes valores como 15 mm, 10 mm y 5 mm y observar y registrar el valor correspondiente en el electrómetro (V); representar V frente a d.
5. Aumentar de nuevo d a ~ 20 mm, inserte un bloque plástico entre las dos placas y observar qué pasa con V que leer por el electrómetro. La reducción de V entre los resultados de las placas (con carga Q fijada en este caso) desde el ε constante dieléctrica más grande de la plástica (frente a aire) como el medio del condensador (vea las ecuaciones 1 y 3).

3. paralelo y serie capacitancias

1. Obtener un capacímetro (un "medidor de LCR" o un multímetro con un modo de medición de capacitancia); obtener un protoboard para facilitar las conexiones eléctricas en esta parte del experimento.
2. Obtener dos condensadores de "cerámica" comerciales con una capacitancia de 1 μF y utilice el medidor de capacitancia para verificar su capacidad, como en la figura 2.
3. Conecte los dos condensadores en paralelo y use el medidor de capacitancia para medir la capacitancia total (entre los puntos A y B, ver figura 3).
4. Conecte los dos condensadores en serie y utilice el medidor de capacitancia para medir la capacitancia total (entre los puntos A y B, ver figura 4).

Figura 3: diagrama que muestra dos capacitores conectados en paralelo.

Figura 4: diagrama que muestra dos capacitores conectados en serie.

Figura 5: diagrama mostrando la carga de un condensador mediante una fuente de tensión, mientras que lee el voltaje con un Electrómetro.

Figura 6: después de desconectar rápidamente la fuente de tensión en la figura 5, el voltaje y la carga en el condensador deben permanecer.

Para un condensador, una parcela de la corriente I versus rampa tipo ΔV/Δt es lineal, como se muestra en la figura 7. Puesto que la corriente es la tasa de cambio en la carga Q en un conductor terminal, esto también refleja la relación lineal entre la carga Q y el voltaje V de un capacitor (ecuación 1). La pendiente de la recta es igual a la capacitancia del condensador (ecuación 2).

Para un condensador de placas paralelas con carga fija Q, una parcela de la tensión V entre las placas y la distancia d entre las placas también debería ser lineal, como se muestra en la figura 8. Esto verifica la ecuación 4, que es una consecuencia de la capacitancia C del condensador de placas paralelas es inversamente proporcional a la distancia d (ecuación 3) y el voltaje V es inversamente proporcional a la capacitancia C (porque la carga Q es fija, ecuación 1).

Para dos capacitores, cada uno con 1 μF de capacidad, su conexión en paralelo debe dar una capacidad total de 2 μF, y su conexión en serie debe medir una capacidad total de 0,5 μF, consistente con las ecuaciones 5 y 6 de las reglas de combinación de capacitancias en paralelo o en serie.

Figura 7 : Una ejemplar trama lineal entre tasa de rampa de corriente y voltaje.

Figura 8 : Una ejemplar trama lineal entre voltaje entre placas y la distancia.

En este experimento, se demostró la carga de un condensador, donde la corriente es el producto de la capacitancia y la tasa de cambio del voltaje. Observando cómo varía el voltaje dado un cargo fijo, hemos demostrado cómo la capacitancia de un condensador de placas paralelas varía con la separación y con el medio entre las placas.

El medidor de capacitancia también puede utilizarse para medir directamente la capacitancia y determinar la capacitancia total de capacitores conectados en paralelo o en serie.

Los condensadores se utilizan en muchas aplicaciones de circuitos. Pueden ser utilizados para almacenar energía y cargos. Son esenciales para el procesamiento de la señal eléctrica. Por ejemplo, tomando la derivada de una señal eléctrica, llamada el "diferenciador", como el condensador corriente, es directamente proporcional a la derivada de una tensión dependiente del tiempo aplicada al condensador. También se utilizan en filtros (la conducción entre los dos conductores que hasta que un condensador aumenta generalmente con mayor frecuencia aunque es muy baja a baja frecuencia).

El autor del experimento agradece la ayuda de Gary Hudson para la preparación de material y Chuanhsun Li para la demostración de los pasos en el video.