Capacitance

Source : Yong P. Chen, PhD, département de physique & astronomie, Faculté des sciences, Université de Purdue, West Lafayette, Indiana

Cette expérience utilisera les condensateurs commerciales et un condensateur à plaques parallèles pour démontrer le concept de capacité. Un condensateur stocke en face de charges sur les deux conducteurs, par exemple deux opposés plaques métalliques, conduisant à une différence de potentiel entre les deux conducteurs (chute de tension). Le montant des frais sur chaque conducteur est proportionnel à cette chute de tension, avec la capacité comme étant le facteur de proportionnalité. Si la tension évolue avec le temps, le courant qui circule dans le condensateur sera proportionnel au taux de ce changement, et encore une fois, la capacité est le facteur de proportionnalité.

La capacité du condensateur à plaques parallèles est le produit de la constante diélectrique avec la distance entre les plaques divisé par la surface de la plaque. Cette expérience démontrera la proportionnalité avec la distance de premier dépôt de certains frais sur le condensateur et ensuite à l’aide d’un voltmètre haute impédance (électromètre) pour surveiller la tension entre les plaques lorsque la distance augmente. Le changement de tension se fera également avec un matériau diélectrique, comme une plaque de plastique inséré dans l’espace entre les plaques de métal.

Un capacimètre serviront directement mesurer la capacité, ainsi que mesure parallèle et raccordement en série de condensateurs disponibles sur le marché et d’étudier comment la capacité totale est liée aux capacités individuelles.

Un condensateur est constitué de deux conducteurs séparés et sa capacité C représente sa « capacité à accumuler charge ». Appliquer une différence de tension V entre ces deux conducteurs peut induire charge + Q sur un chef d’orchestre et Q sur l’autre conducteur (donc la charge totale est nulle, c'est-à-dire, le condensateur dans son ensemble est charge neutre), tels que :

(Équation 1)

Notez ici que Q est la charge sur un conducteur (pas la charge totale sur les deux conducteurs qui serait 0). Si la tension V évolue avec le temps, il en sera la charge Q. Si V et Q changent par ΔV et ΔQ, respectivement dans un Δt d’intervalle de temps, puis,

ΔQ = C • ΔV

et

Depuis ΔQ/Δt le courant (appelé « courant de charge ») circule dans le conducteur chargé positivement du condensateur, puis comme indiqué dans l’équation 2:

(Équation 2)

Cela signifie que la capacité est le facteur de proportionnalité afin de convertir le taux de variation de tension (ΔV/Δt) pour le courant qui circule dans le condensateur (voir Figure 1).

La capacité peut également être mesurée directement à l’aide d’un capacimètre (par exemple, en utilisant le mode de mesure de capacité d’un multimètre ou « RLC » ; voir Figure 2).

Le plus simple type de condensateur, représentée dans les Figures 1 et 2, se compose de deux plaques conductrices parallèles et s’appelle un « condensateur à plaques parallèles ». Sa capacité C est donnée par l’équation 3

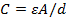(Équation 3)

où : A représente la zone de la plaque, d est la séparation entre les plaques et la constante diélectrique du milieu entre les deux plaques (ou « remplir » le condensateur). Le support doit être électriquement isolantes. Pour un vide,

F/m

Cette valeur est généralement notée ε₀, qui décrit aussi ε d’air permettant une bonne approximation. Autre moyen, comme le pétrole, ont généralement une plus grande ε, qui est mise à l’échelle de la valeur vide ε₀ cité plus haut par un facteur supérieur à un. Ce facteur est connu comme le « relative » constante diélectrique ou permittivité du milieu et communément appelé κ. Un tel milieu est aussi communément appelé un « matériau diélectrique ».

Par conséquent, pour un condensateur à plaques parallèles :

Si la charge Q est fixée, avant d’augmenter la plaque séparation d augmentera la tension V (proportionnellement à d) :

(Équation 4)

Condensateurs peuvent être connectés en parallèle ou en série à l’instar de résistances. La capacité totale « effective » est capacitances liés à individuels dans une connexion parallèle ou série semblable à la conductance électrique comment d’une parallèle/série, connexion de la résistance est conductances liés à différents. Ainsi, pour les deux condensateurs avec capacitances C₁ et C₂, la capacité totale pour un branchement en parallèle est égale à la somme des deux capacités. Ou,

(Équation 5)

Pour une connexion série,

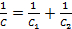(Équation 6)

Ces deux types de connexions sont représentés dans les Figures 3 et 4.

Figure 1 : Schéma montrant un condensateur connecté à une source de tension utilisée pour charger le condensateur et un ampèremètre pour lire le courant.

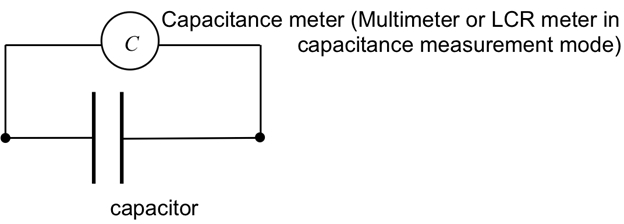
Figure 2 : Schéma montrant un capacimètre relié à un condensateur de mesurer directement la capacité.

1. charge d’un condensateur

1. Obtenir un condensateur commercial avec capacité C = 470 µF (ou une valeur similaire), une source de tension programmables et un ampèremètre (ou multimètre qui peut mesurer le courant).
2. Avec la source de tension définie à 0 V, raccordez la borne « + » de la source de tension aux bornes du condensateur, avec l’ampèremètre entre les deux et raccordez la « − » de la source de tension à l’autre borne, comme dans la Figure 1. La connexion peut être établie avec les câbles avec des pinces ou des fiches banane en recevant des ports sur le condensateur et les instruments.
3. Changer la source de tension de 0 V à 1 V (dans environ 1 s), et observez le transitoire actuel de lecture sur l’ampèremètre. Faites de même pour les 2 V, 5 V et 10 V (pour chaque tension cible ; cela signifie premier aller retour à 0 V, puis basculez la tension cible dans environ 1 s). Notez que le courant transitoire est plus grand pour une plus grande tension de cible, comme prévu de l’équation 2.
4. Programme la source de tension pour générer une rampe de tension de 0 V à 10 V à 5 s et d’enregistrer la lecture de « état stationnaire » de l’amp-compteur au milieu de la rampe. Répéter pour une durée de rampe de 10 s, 20 s et 30 s. intrigue le courant observé par rapport à la vitesse de montée de tension (en V/s).

2. réglage de la capacité

1. Éteignez la source de tension et remplacez-la par une batterie V 300 et remplacer l’ampèremètre par une résistance de MΩ 1 (cette résistance vise à fournir une protection supplémentaire pour limiter le courant dans le circuit) ; remplacer le condensateur commercial avec un condensateur à plaques parallèles avec une séparation réglable entre les plaques.
2. Procurez-vous un voltmètre haute impédance (ou « électromètre ») et connectez-le pour mesurer la différence de tension V entre les deux plaques (la haute impédance empêche la décharge du condensateur au cours de l’expérience lorsque l’électromètre est connecté). Voir la Figure 5.
3. Connecter la batterie V 300 pour le condensateur à plaques parallèles, attendre que l’électromètre atteint l’état d’équilibre de 300 V (maintenant le condensateur est complètement chargé par la source de V 300) et puis déconnecter rapidement la source de tension des plaques. Voir la Figure 6. L’électromètre doit toujours lire 300 V.
4. Maintenant augmenter la distance d entre les plaques à des valeurs plus élevées comme 15 mm, 10 mm et 5 mm et observer et enregistrer la tension correspondante de lecture sur l’électromètre (V) ; terrain V par rapport à d.
5. Augmenter d retour à ~ 20 mm, insérer une plaque en plastique entre les deux plaques et observer ce qui arrive à V lu par l’électromètre. La réduction de V entre les résultats de plaques (avec charge Q fixé dans ce cas) de la plus grande ε de la constante diélectrique du plastique (par rapport à l’air) comme le support du condensateur (voir équations 1 et 3).

3. parallèle et série Capacitances

1. Obtenir un capacimètre (un « RLC » ou un multimètre avec un mode de mesure de capacité) ; obtenir une carte de prototypage pour faciliter les connexions électriques dans cette partie de l’expérience.
2. Obtenir deux condensateurs « céramiques » commerciales avec une capacité de 1 µF et le capacimètre permet de vérifier leur capacité, comme illustré Figure 2.
3. Connectez les deux condensateurs en parallèle et le capacimètre permet de mesurer la capacité totale (entre les points A et B, voir Figure 3).
4. Connectez les deux condensateurs en série et le capacimètre permet de mesurer la capacité totale (entre les points A et B, voir Figure 4).

Figure 3: diagramme montrant deux condensateurs reliés en parallèle.

Figure 4: diagramme montrant deux condensateurs reliés en série.

Figure 5: Schéma montrant la charge d’un condensateur à l’aide d’une source de tension, lors de la lecture de la tension avec un électromètre.

Figure 6: après avoir rapidement déconnecté de la source de tension dans la Figure 5, la tension et la charge sur le condensateur doivent rester.

Pour un condensateur, une parcelle de courant j’ai par rapport aux taux de rampe ΔV/Δt est linéaire, comme illustré à la Figure 7. Puisque le courant est le taux de la variation de la charge Q sur un terminal des conducteurs, cela reflète également la relation linéaire entre la charge Q et de la tension V pour un condensateur (équation 1). La pente de la courbe est égale à la capacité du condensateur (équation 2).

Pour un condensateur à plaques parallèles avec forfait Q, une parcelle de la tension V entre les plaques par rapport à la distance d entre les plaques devrait également être linéaire, comme illustré à la Figure 8. Il vérifie l' équation 4, qui est une conséquence de la capacité C du condensateur plaques parallèles étant inversement proportionnelle à la distance d (équation 3) et la tension V étant inversement proportionnelle à la capacité C (parce que la charge Q est fixe, l’équation 1).

Pour les deux condensateurs, chacune ayant 1 μF de capacitance, leur connexion parallèle devrait donner une capacité totale de 2 µF, et leur connexion série doit mesurer une capacité totale de 0,5 µF, compatible avec les équations 5 et 6 sur les règles de la combinaison de capacités en parallèle ou en série.

Figure 7 : Un exemplaire tracé linéaire entre la vitesse de montée de courant et de tension.

Figure 8 : Un tracé linéaire exemplaire entre inter-plaques entre tension et distance.

Dans cette expérience, il a été démontré de la charge d’un condensateur, où le courant est le produit de la capacité et le taux de variation de tension. En observant comment la tension varie compte tenu d’une charge fixe, nous avons démontré comment la capacité d’un condensateur à plaques parallèles varie avec la séparation et avec le milieu entre les plaques.

Le capacimètre permet également de mesurer directement la capacitance et déterminer la capacité totale pour les condensateurs reliés en parallèle ou en série.

Condensateurs sont couramment utilisés dans de nombreuses applications de circuit. Ils peuvent servir à stocker des frais et l’énergie. Ils sont indispensables pour le traitement du signal électrique. Par exemple, prenant la dérivée d’un signal électrique, dite le « facteur de différenciation », comme le condensateur courant, est directement proportionnelle à la dérivée d’une tension de charge de temps appliquée au condensateur. Ils sont également utilisés dans les filtres (la conduction entre les deux conducteurs constituant qu'un condensateur augmente généralement à plus haute fréquence, bien qu’il soit très faible à basse fréquence).

L’auteur de l’expérience reconnaît l’aide de Gary Hudson pour la préparation du matériel et Chuanhsun Li pour démontrer les étapes dans la vidéo.