Nozzle Analysis: Variations in Mach Number and Pressure Along a Converging and a Converging-diverging Nozzle

Source: Shreyas Narsipur, Mechanical and Aerospace Engineering, North Carolina State University, Raleigh, NC

A nozzle is a device that is commonly used to accelerate or decelerate flow by virtue of its varying cross-section. Nozzles are widely used in aerospace propulsion systems. In rockets, propellant that is ejected from the chamber is accelerated through a nozzle to create a reaction force that propels the system. In jet engines, a nozzle is used to transform energy from a high-pressure source into kinetic energy of the exhaust to produce thrust. The isentropic model along the nozzle is sufficient for a first-order analysis as the flow in a nozzle is very rapid (and thus adiabatic to a first approximation) with very little frictional loses (because the flow is nearly one-dimensional with a favorable pressure gradient, except if shock waves form and nozzles are relatively short).

In this experiment, two types of nozzles are mounted on a nozzle test rig, and a pressure flow is created using a compressed air source. The nozzles are run for different back-pressure settings to analyze the internal flow in the nozzles under varying flow conditions, identify the various flow regimes, and compare the data to theoretical predictions.

A nozzle begins at the point where the chamber diameter begins to decrease. There are two main types of nozzles: the converging nozzle and the converging-diverging nozzle. One of the governing isentropic relations between Mach number (M), nozzle area (A), and velocity (u) is represented by the following equation:

 (1)

where u is the velocity, A is the nozzle area, and M is the Mach number. Based on Equation 2,

1. At M = 0, the flow is static, i.e., no-flow condition exists
2. At 0 < M < 1, as the area decreases, a proportional increase in the velocity of the flow is observed
3. At M ≥ 1, any increase in area will produce a proportional increase in speed

Converging nozzles, as shown in Figure 1, are tubes with an area that decreases from the nozzle entry to the exit (or throat) of the nozzle. As the nozzle area decreases, the flow velocity increases, with the maximum flow velocity occurring at the nozzle throat. As the inlet flow velocity is increased, flow velocity at the nozzle throat keeps increasing until it reaches Mach 1. At this point, the flow at the throat gets choked, meaning that any further increase of inlet flow velocity will not increase the flow velocity at the throat. It is for this reason that converging nozzles are used to accelerate fluids in the subsonic flow regime alone and can commonly be found on all commercial jets (except for the Concord) as they travel at subsonic speeds.

Figure 1. Schematic of a converging nozzle. Please click here to view a larger version of this figure.

For vehicles like rockets and military aircraft, which must travel at and above the speed of sound, a converging-diverging nozzle, as illustrated in Figure 2, is used. In a converging-diverging nozzle, the converging section is followed by a divergent nozzle section and is designed in a way such that flow gets choked at the throat of the converging section, thereby fixing the mass flow rate in the system. The flow is then isentropically expanded to reach supersonic Mach numbers in the diverging section. The supersonic flow velocities set in the diverging section are a function of the nozzle area ratios after the throat. Based on the design of the converging-diverging nozzle, the flow velocity after the nozzle throat can either: (i) decrease to subsonic velocities, (ii) become supersonic, cause a normal shock, and then decrease to subsonic velocities at the nozzle exit, or (iii) remain supersonic throughout the diverging section. The amount of thrust produced by the nozzle depends on the exit velocity and pressure and the mass flow rate through the nozzle.

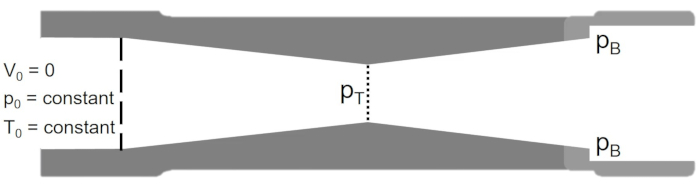
Figure 2. Schematic of a converging-diverging nozzle. Please click here to view a larger version of this figure.

The back-pressure (p_B) is the driving factor that determines the flow condition in the nozzle. When the stagnation pressure, p_O = p_B, there is no flow through the nozzle. As p_B is reduced, the Mach number at the throat (p_T) increases until the flow is choked (M_T = 1). The condition at which choked flow occurs can be calculated using the isentropic relation:

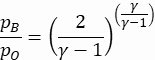 (2)

where γ is the specific heat ratio of the fluid. Substituting γ = 1.4 (specific heat ratio for dry air) in Equation 2, we obtain a back-pressure ratio of:  

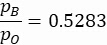 (3)

Equation 3 defines the boundary between the non-choked and choked flow regimes. When flow is choked, the Mach number no longer increases and is capped at M = 1.

In the case of a converging nozzle, the exit of the nozzle corresponds to the nozzle throat (as seen in Figure 1); therefore, the Mach number right at the exit does not exceed 1, i.e., the flow never goes supersonic. Once the flow exits the nozzle, it undergoes an expansion, due to the sudden increase in area that could lead to (uncontrolled) supersonic flow velocities.

Based on Figure 3, the following are the flow conditions that can be observed in a converging nozzle:

1. No flow condition, where the back-pressure is equal to the total pressure.
2. Subsonic flow, where the flow accelerates as area decreases, and the pressure drops.
3. Subsonic flow, where there is significantly higher acceleration and the pressure drops.
4. Choked flow, where any pressure drop does not accelerate the flow.
5. Choked flow, where the flow expands after the nozzle exit (considered non-isentropic).

Figure 3. Flow conditions and regimes in a converging nozzle (theoretical predictions). Please click here to view a larger version of this figure.

The mass flow parameter (MFP) is a variable that determines the rate at which mass is flowing through the nozzle and is given by the equation:

 (4)

Here,  is the mass flow rate through the nozzle, T_O is the stagnation temperature, and A_T is the area of the throat, which, in the case of the converging nozzle, is equal to the area at the nozzle exit, A_E. As observed in Figure 3, until choked flow, the MFP continues to increase. Once the flow is choked, the mass flow rate is fixed, and the MFP remains a constant for decreasing back-pressure ratios.

In order to achieve controlled supersonic flows in a nozzle, a diverging section needs to be introduced after the throat of a converging nozzle, as illustrated in Figure 2. Once the flow becomes choked at the throat of a converging-diverging nozzle (based on Equation 3), three possible flow conditions can occur: subsonic isentropic flow (the flow decelerates after the choked condition), supersonic non-isentropic flow (where the flow accelerates supersonically, forms a shock wave - a thin region of coalesced molecules that forms normal to a certain point on the nozzle and causes a sudden change in flow conditions, generally referred to as a normal shock - and decelerates subsonically after the shock), or supersonic isentropic flow (where the flow accelerates supersonically after the choked condition). Figure 4 shows the following seven profiles in the position versus pressure ratio plot. Note that the first vertical dashed line on the left of the p/p_O versus distance along the nozzle plot is the location of the throat, the second vertical dashed line is the location of the nozzle exit, and the horizontal dashed line marks the choked condition.

1. Subsonic flow that never reaches choked condition.
2. Subsonic flow that reaches choked condition but does not attain supersonic velocities (considered isentropic).
3. Subsonic flow that reaches choked condition, with the resulting supersonic flow forming a normal shock, which then experiences subsonic deceleration. Here, the normal shock causes a sudden drop in velocity and an increase in back-pressure, as indicated by the sudden increase in p/p_O.
4. Subsonic flow that reaches choked condition, with the resulting supersonic flow forming a normal shock after the nozzle (considered isentropic in the nozzle).
5. Over-expanded flow – the pressure at the nozzle exit is lower than the ambient pressure, causing the jet exiting the nozzle to be highly unstable with huge variations in pressure and velocity as it travels downstream.
6. Flow after the choked condition is supersonic through the nozzle, and no shock is formed.
7. Under-expanded flow – the pressure at the nozzle exit is higher than the ambient pressure and results in similar effects as over-expanded flow.

Figure 4. Flow conditions and regimes in a converging-diverging nozzle (theoretical predictions). Please click here to view a larger version of this figure.

In this demonstration, a nozzle test rig was used, which consisted of a compressed air source that channels high-pressure air through the nozzles being tested, as shown in Figure 5. The flow pressure ranges from 0 - 120 psi and is controlled using a mechanical valve. While the pressures are measured using an external sensor, the mass flow rates in the nozzle are measured by a pair of rotameters placed right before the exhaust of the nozzle test rig.

Figure 5. Nozzle test rig. Please click here to view a larger version of this figure.

1. Measuring Axial Pressure in Converging and Converging-diverging Nozzles

1. Mount the converging nozzle in the center of the nozzle test rig, as shown in Figure 5. The 2-D section for the converging nozzle with labels for the pressure taps are shown in Figure 6.

Figure 6. Geometry of converging nozzle. Please click here to view a larger version of this figure.

2. Connect the 10 static pressure ports and the stagnation pressure port to the pressure measurement system using flexible, high-pressure PVC tubes.
3. Connect the pressure measurement system to the graphical software interface for real-time pressure data reading.
4. Take the zero/no-flow condition reading.
5. Open the mechanical flow control valve to start the airflow.
6. Rotate the valve to adjust the flow rate to obtain a back-pressure ratio (p_B/p_O) of 0.9. Note that the back-pressure for both the converging and converging-diverging nozzles correspond to the pressure data read-out from port 10.
7. Record the data corresponding to Table 1.
8. Decrease the back-pressure ratio in steps of 0.1 until p_B/p_O = 0.1 repeating step 7 for each setting. Additionally, repeat step 7 for a p_B/p_O = 0.5283 to capture flow data at the theoretical choked flow condition.
9. Replace the converging nozzle with the converging-diverging nozzle and repeat steps 1.2 - 1.8. The 2-D section for the converging nozzle with labels for the pressure taps are shown in Figure 7.
10. On completion of the tests, disconnect all systems and dismantle the nozzle test-rig.

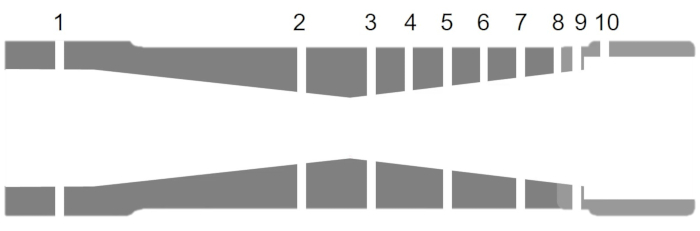
Figure 7. Geometry of converging-diverging nozzle. Please click here to view a larger version of this figure.

Table 1. Data collected for the nozzle experiment.

Tap number	Axial Position of Tap (in)	Nozzle Area Ratio (A/Ai)	Pstatic (psi)	Po (psi)	Mass Flow Rate (slugs/s)	Patm (psi)	To (°F)
Figure 6/7	Table 2	Table 2	Gauge pressure	Gauge pressure	Rotameter	Gauge pressure	Temperature sensor

Table 2. Nozzle geometry data.

Tap number	Converging Nozzle		Converging-Diverging Nozzle
	Axial Position of Tap (in)	Nozzle Area Ratio (A/Ai)	Axial Position of Tap (in)	Nozzle Area Ratio (A/Ai)
1	0	60.14	0	60.14
2	1	51.379	4.5	6.093
3	2	35.914	6.5	1
4	3	23.218	6.9075	1.053
5	4	13.275	7.3795	1.222
6	5	6.094	7.8515	1.403
7	5.5	3.54	8.3235	1.595
8	6	1.672	8.7955	1.802
9	6.5	1	9.2675	2.02
10	7	60.041	9.5	60.041

The following constants were used in the analysis: specific heat of dry air, γ: 1.4; reference nozzle area, A_i = 0.0491 in², and standard atmospheric pressure, P_atm = 14.1 psi. Figures 8 and 9 show the variation in pressure ratio and Mach number across the length of the nozzle (normalized based on total nozzle length) for various back-pressure settings for the converging and converging-diverging nozzles, respectively. The mass flow parameter versus the back-pressure ratio is also plotted and studied for both the nozzles.

From Figure 8, we observe that as the p_B/p_O ratio decreases(until 0.5283), flow at every section of the nozzle is subsonic and increases with decreasing area. At and below p_B/p_O = 0.5283, the Mach number at the throat (normalized nozzle distance = 0.93) does not exceed one. This clearly demonstrates that the flow is choked at the throat. Beyond the throat/nozzle exit, there is uncontrolled expansion of the flow, leading to supersonic Mach numbers. The overall trends in p/p_O distribution matches theoretical trends from Figure 3. The trends in MFP follow theoretical results until p_B/p_O = 0.6 but start decreasing instead of plateauing for lower values of back-pressure ratios. Given that the flow is choked, the MFP should be constant. However, based on the location of the tap measuring the throat pressure (tap 9, Figure 6), we see that the measurements are taken slightly before the true nozzle throat that in turn leads to an incorrect measurement of the MFP.

For the converging-diverging nozzle (Figure 9), subsonic flow is observed until p/p_O at the throat (normalized nozzle distance = 0.68) equals 0.5283 (choked flow condition). Further reduction of p_B/p_O shows three distinct patterns:
a. Pattern 1 - Flow reaches choked condition at the throat and decelerates subsonically in the diverging section (0.8 < p_B/p_O < 0.7).
b. Pattern 2 - Flow accelerates supersonically beyond the throat, forms a shock in the diverging section, and decelerates (in some cases to subsonic velocities) for 0.7 < p_B/p_O < 0.3.
c. Pattern 3 - Flow continues to accelerate supersonically for the entirety of the diverging section for p_B/p_O values lower than 0.3.

The MFP increases with decreasing back-pressure ratios, peaks at p_B/p_O = 0.5, and starts decreasing instead of remaining constant as predicted by theory.

Figure 8. Results for the converging nozzle (from top-right, clockwise) variation in pressure ratio across the nozzle; variation in Mach number across the nozzle; and variation in mass plow parameter with back-pressure ratio. Please click here to view a larger version of this figure.

Nozzles are commonly used in aircraft and rocket propulsion systems as they offer a simple and effective method to accelerate flow in restricted distances. In order to design nozzles to suit a given application, an understanding of the flow behavior and factors that affect said behavior for a range of flow conditions is essential for designing efficient propulsion systems. In this demonstration, the converging and converging-diverging nozzles - two of the most common nozzle types used in aerospace applications - were tested using a nozzle test rig. The pressure and Mach number variations across the two nozzles were studied for a wide range of flow conditions.

Results for the converging nozzle tests showed that the maximum limit up to which flow can be accelerated is M = 1, at which point flow at the nozzle throat gets choked. Once flow is choked, any increase in inlet flow velocity did not increase the flow velocity at the throat/exit to supersonic speeds. Analysis of the converging-diverging nozzle provides insight into how supersonic flow velocities can be achieved once flow gets choked at the throat. We also observed three types of flows that can be obtained after the choked throat depending on the back-pressure ratio of the flow. A comparison of the pressure trends obtained for both the converging and converging-diverging type nozzles with theoretical results was excellent. However, the experimental results showed the mass flow parameter decreasing for lower values of back-pressure ratio instead of plateauing once the maximum value was achieved, as predicted by theory. 

Figure 9. Results for the converging-diverging nozzle (from top-right, clockwise) variation in pressure ratio across the nozzle; variation in Mach number across the nozzle; and variation in mass plow parameter with back-pressure ratio. Please click here to view a larger version of this figure.