Method Article
Quantitative Analysis of Viscoelastic Properties of Red Blood Cells Using Optical Tweezers and Defocusing Microscopy
* These authors contributed equally
In This Article
Summary
Here, an integrated protocol based on optical tweezers and defocusing microscopy is described to measure the rheological properties of cells. This protocol has wide applicability in studying the viscoelastic properties of erythrocytes under variable physio-pathological conditions.
Abstract
The viscoelastic properties of erythrocytes have been investigated by a range of techniques. However, the reported experimental data vary. This is not only attributed to the normal variability of cells, but also to the differences in methods and models of cell response. Here, an integrated protocol using optical tweezers and defocusing microscopy is employed to obtain the rheological features of red blood cells in the frequency range of 1 Hz to 35 Hz. While optical tweezers are utilized to measure the erythrocyte-complex elastic constant, defocusing microscopy is able to obtain the cell height profile, volume, and its form factor a parameter that allows conversion of complex elastic constant into complex shear modulus. Moreover, applying a soft glassy rheology model, the scaling exponent for both moduli can be obtained. The developed methodology allows to explore the mechanical behavior of red blood cells, characterizing their viscoelastic parameters, obtained under well-defined experimental conditions, for several physiological and pathological conditions.
Introduction
Mature red blood cells (RBCs), also known as erythrocytes, are able to extend more than twice their size when passing through the narrowest capillaries of the human body1. Such capacity is attributed to their unique ability to deform when subjected to external loads.
In recent years, different studies have characterized this feature in RBC surfaces2,3. The area of physics that describes the elastic and viscous responses of materials due to external loads is called rheology. In general, when an external force is applied, the resulting deformation depends on the material's properties and can be divided into elastic deformations, that store energy, or viscous deformations, that dissipate energy4. All cells, including RBCs, exhibit a viscoelastic behavior; in other words, energy is both stored and dissipated. The viscoelastic response of a cell can thus be characterized by its complex shear modulus G*(ω) = G'(ω) + iG"(ω), where G' (ω) is the storage modulus, related to the elastic behavior, and G" (ω) is the loss modulus, related to its viscosity4. Moreover, phenomenological models have been used to describe cell responses, one of the most used is called the soft glassy rheology model5, characterized by a power-law dependence of the complex shear modulus with the load frequency.
Single-cell-based methods have been employed to characterize the viscoelastic properties of RBCs, by applying force and measuring displacement as a function of the imposed load2,3. However, for the complex shear modulus, few results can be found in the literature. Using dynamic light scattering, values for RBC storage and loss moduli were reported varying from 0.01-1 Pa, in the frequency range of 1-100 Hz6. By using optical magnetic twisting cytometry, an apparent complex elastic modulus was obtained7, and for comparison purposes, a multiplicative factor was claimed to possibly clarify the discrepancies.
More recently, a new methodology based on optical tweezers (OT) together with defocusing microscopy (DM), as an integrated tool to quantitatively map the storage and loss of shear moduli of human erythrocytes over time-dependent loads, was established8,9. In addition, a soft glassy rheology model was used to fit the results and obtain a power-law coefficient that characterizes the RBCs8,9.
Overall, the developed methodology8,9, the protocol for which is described in detail below, clarifies previous discrepancies by using the measured values for the form factor, Ff, that relates forces and deformations to stresses and strains in the RBC surface and can be utilized as a novel diagnostic method capable of quantitatively determining the viscoelastic parameters and soft glassy features of RBCs obtained from individuals with different blood pathologies. Such characterization, using the protocol described below, may open up new possibilities to understand the behavior of RBCs from a mechanobiological perspective.
Protocol
Human blood samples were provided by adult men and women volunteers according to protocols approved by the Research Ethics Committee of the Federal University of Rio de Janeiro (Protocol 2.889.952) and registered in Brazil Platform under CAAE number 88140418.5.0000.5699. A written form of consent was issued to and collected from all volunteers. Those with any hemoglobinopathy and/or taking controlled medication were excluded. The entire process followed the guidelines approved by the institute's ethical committee.
1. Preparation of sample holders
- Acquire two coverslips (24 mm x 60 mm and 24 mm x 32 mm; thickness = 0.13-0.17 mm) and one rubber ring (diameter = 10 mm; thickness = 2 mm) for each sample holder.
- Pour silicone grease over the rubber ring surface in a way that covers the entire perimeter.
- Place the rubber ring on the coverslip with the grease side facing the coverslip. Wait for 5 min for proper attachment, the sample holders are then ready to receive the cell culture.
NOTE: In addition, either commercial or homemade glass bottom dishes can also be used, as previously described10.
2. Cell culture
NOTE: The steps below describe how to obtain healthy RBCs from human blood. It is important that the samples are freshly prepared before each experiment.
- Dilute 20 µL of blood in 250 µL of 1x phosphate buffer saline (PBS) solution containing 137 mM NaCl, 2.7 mM KCl, 10 mM Na2HPO4, 1.8 mM KH2PO4, 10 mM glucose, and supplemented with 1 mg/mL bovine serum albumin (BSA).
- After centrifugation at 200 x g for 2 min at room temperature, aspirate the supernatant using a pipette and resuspend the cell pellet in 1mL of 1x PBS/BSA solution. Wash the cells 2x in the buffer.
- Calculate cell density using a haemocytometrer and seed 50,000 to 100,000 cells in the sample holder prepared in step 1. Wait for 10-15 min for nonspecific cell attachment to the coverslip; the waiting time does not affect cells.
- Add to the sample 0.2 µL of a 10% v/v polystyrene sphere solution (radius = 1.52 ± 0.02 µm) for further OT experiments. Confirm proper mixing by looking at the samples under the microscope.
- After cells seeding, just place the second coverslip above the rubber ring (it is not necessary to add grease for attachment), close the setup, and finish the sample preparation. Samples are ready for microscopy analysis and manipulation.
3. Optical tweezers microscope setup
NOTE: OT are tools that use a highly focused laser beam to trap microscopic objects and to measure forces in the piconewton range and displacements in the nanometer scale. The OT laser used (1064 nm wavelength) must be properly aligned, as previously described10.
- Briefly, using at least two mirrors separated by a distance of a few centimeters (10-20 cm at least), direct a linearly polarized laser beam toward the back entrance of an inverted microscope. Precisely align the laser beam to enter the microscope in a straight line (Figure 1).
- Then, reflect the laser beam using a dichroic mirror, installed in the microscope, to proceed parallel to the axis of the objective lens and enter the lens near the center of its back entrance. This will focus the laser to create the optical trap (Figure 1).
- Next, to measure forces with OT, calibrate the system to obtain the trap stiffness (κOT). See10 for a more detailed description of the OT calibration procedure. Once κOT is found, the OT system is ready for the rheology experiments.
4. DM setup
NOTE: DM is a brightfield-based optical microscopy technique that allows transparent objects to become visible if the microscope is slightly defocused11,12. Such a technique has been applied to obtain the RBC shape13. The same microscope employed for the OT system can be used for DM, to obtain a height profile through 3D reconstructions.
- Adjust the microscope lighting system by performing the Köhler illumination14 and, for better resolution, fully open the condenser-diaphragm to perform the experiments.
- Use a piezoelectric positioning system to displace the sample in all coordinates, with nanometric precision in the z-axis. Perform the autocalibration of the piezoelectric system on all axes. Once all the procedures are performed, the microscope system is ready for DM experiments.
5. OT-based rheology experiment and analysis
NOTE: The rheology experiment consists of observing the responses of the cell to small oscillations of varying frequencies.
- Experimentation
- Using the OT system, trap the sphere with the OT laser and then attach it to an RBC by pressing the sphere against the cell surface near to the top surface and close to the cell edge. Use the microscope for this step. Then, trap another sphere and repeat the same attachment procedure but now attach it to the coverslip, close to the cell. The sphere attached to the coverslip is the reference bead (Figure 2), which is necessary to follow the piezo displacement and to compare with the RBC sphere.
- Make sure that the chosen cell is well attached to the coverslip and that the RBC and reference spheres have adhered to the RBC surface and coverslip, respectively, before starting the measurement. Visually identify the non-adhered cells as they will move over time, despite the high adhesion rate (around 80%-90%).
- Add a sinusoidal function of amplitude, ξ0 = 0.500 ± 0.001 μm and varying frequencies of 1 Hz, 7 Hz, 14 Hz, 21 Hz, 28 Hz, and 35 Hz, with respective angular frequencies, ω, of 6.3 rad/s, 169 rad/s, 88 rad/s, 132 rad/s, 176 rad/s, and 220 rad/s, to the piezoelectric stage software, using the piezoelectric software, as previously demonstrated8,9.
- Using the piezoelectric stage, press the start button to allow the piezoelectric displacement and keep the RBC sphere in the trap, submit the sample to a cycle of movements using the sinusoidal function previously set. Use a camera capable of producing images at 790 frames/s or higher to record the sample movement. A schematic of the experiment is shown in Figure 2.
- While the sample is submitted to sinusoidal movements, activate the OT to trap the sphere attached to the RBC surface. Regardless of the temperature chosen to carry out the experiments, room temperature, 37 °C, or another temperature, carefully monitor the temperature to avoid variations during the measurements. The infrared (1064 nm) laser used to create the OT causes almost no damage or heating of the cells.
- Analysis
- Analyze the images obtained during the sinusoidal movements using ImageJ to find the center of mass position of each of the spheres over time.
NOTE: These data allow generating plots capable of showing phase and amplitude differences between both spheres. Such information is crucial for obtaining the viscoelastic response of RBCs. - To obtain the center of mass for each of the spheres, open the ImageJ software. Import the entire movie obtained during the sinusoidal movements.
- In the Image tab, click on Adjust, and then select Threshold. The threshold window will open. Select B&W. This will turn the background white and the spheres black.
- Adjust the threshold with both scrollbars under the histogram in order that both spheres appear with the maximum amount of pixels.
- Select the reference sphere by clicking on File > Rectangle. Draw a rectangle to select the sphere. After selecting the reference sphere in one image, make sure the rectangle also correctly selects the same sphere in all other images of the movie.
- Then, in the Analyze tab, click on Set Measurements and select the Center of Mass option.
- Click again on the Analyze tab and select Analyze Particles. A new window will open. Define the size and circularity (depending on the sphere radius). Check the following boxes Display Results and Clear Results. Finally, click on OK to process all the images.
- A new window containing a table with xy coordinates for the center of the mass will appear. Save these coordinate values as a .txt file. Repeat the procedure for the other sphere, attached to the RBC surface.
- To obtain the amplitude and differences in phase for both spheres, open the analysis software. Import the .txt files previously obtained.
- Create a new table with three columns. In the first column (c0) add the number of frames, in the second column (c1) add the x coordinates for the reference sphere, and in the third column (c2), the x coordinates for the sphere attached to the RBC surface.
NOTE: In this example, as the sinusoidal movements were performed only in the x-axis, it is only necessary to use the x coordinates for both spheres. - Next, correlate the frames with time. Click on Windows > Formula Entry. A new window called formula entry will open. In this window, it is possible to set up eight different equations, each of them in a specific key (from F1 to F8).
- Select F1, type the following formula:
c3 = c0 / (camera fps)
Click on Run. This will create a new column for a time in the table (column 4). - Subtract the x coordinate value of each frame by its respective mean value. To do this, designate any two keys on the formula entry and type the following equations for each key:
c4 = (c1 - mean(c1)) and c5 = (c2 - mean(c2))
Click on the Run button. The results will appear in columns 5 and 6 for reference and RBC spheres, respectively. - Convert the center of mass values from pixels to micrometers. For this, use another key on the formula entry and type the following equation:
c4 = c 4 / conversion number
Repeat the same process for column 5.
NOTE: Conversion is acquired using a micrometer scale/ruler and obtaining its image with the same microscope setup used for the measurements (including the same objective lens). This procedure can be performed during the microscope calibration. A pixel/micrometer relation is thus obtained. - Generate a plot with the centers of mass of both spheres on the y-axis and time on the x-axis. For this, click on Gallery > Linear and Scatter. A new window will open. Select the time column for the x-axis and in the y-axis select the columns of the center of mass in micrometers for both reference and RBC spheres.
- In the plot, select only the data related to the first angular frequency (6.3 rad/s). Use the tools indicated in Figure 3.
- Define the equation that adjusts the data curve for the reference sphere. For this, click on Curve Fit > General and Fit1, select the box of data related to the position of the reference sphere, and then click on Define. A new window will open to define the equation. The position ξ(t) of the reference sphere is described by:
ξ(t) = ξ0cos(ωt)
where ξ is the sinusoidal movement of the sample, ω is the angular frequency and t is the time in s. Transposing this equation to the analysis software, it will look as follows:
 , where m1 is ξ, m2 is f, m0 is the time t, and m3 is the phase of the cosine function for t = 0.
, where m1 is ξ, m2 is f, m0 is the time t, and m3 is the phase of the cosine function for t = 0. - Estimate the values for m1, m2, and m3 from the plot. After defining the equation, click on OK. The data will be fitted based on the equation and a curve together with a small square will appear in the graph with the values of m1, m2, and m3.
- Define the equation that adjusts the data curve for the RBC sphere. For this, click on Curve Fit > General and define the equation that will adjust the curve for the data. The position ρ(t) of the RBC sphere is given by:

where ξ' is the out of phase-amplitude, and φ is the out of phase angle. Transposing this formula to the analysis software, it will look as follows:
 , where m1, m2, and m3 are the values obtained in the curve fit of the reference sphere. m4 is ξ' and m5 is φ.
, where m1, m2, and m3 are the values obtained in the curve fit of the reference sphere. m4 is ξ' and m5 is φ. - Estimate the values for m4 and m5 from the plot. After defining the formula, click on OK. The data will be fitted based on the equation, and a curve together with a small square will appear in the graph with the values of m4 and m5.
- Next, create a new table to add the data obtained from the curve fitting in their respective columns. Define five different columns for the following parameters: angular frequency, amplitude (reference sphere), initial time, amplitude (RBC sphere), and out of phase angle. Perform the same procedure for all other frequencies.
- Use the following equations to find the storage (K') and loss constants (K"):
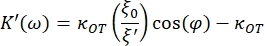

where κOT is the OT elastic constant and β is the Stokes drag coefficient. Transposing the equations to the analysis software, it will look as follows:
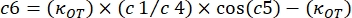 , and
, and
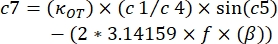 , where β and κOT needs to be replaced by the values found in the system.
, where β and κOT needs to be replaced by the values found in the system. - Plot the results on a graph, using the x-axis for K" and the y-axis for K' (Figure 4).
- Analyze the images obtained during the sinusoidal movements using ImageJ to find the center of mass position of each of the spheres over time.
6. DM experiment and analysis to obtain the overall cell form factor
- Video acquisition
- Move the piezoelectric stage in the xy direction using the software to search for an isolated cell attached to the coverslip. Trap and attach a polystyrene sphere of known diameter to the RBC surface. Using the piezoelectric stage, slightly move the trapped bead, also attached to the RBC surface, in order to deform the cell, and then attach the bead to the coverslip.
NOTE: It is also possible to use the same cell from the OT measurements. - Change the z-axis position to find the focused image, where the focus plane is in the middle of the chosen cell. This image presents the smaller contrast with the gray level in the center of the cell equal to the gray level outside the cell (background).
- When the position is fixed, use the camera software to create a movie of the entire cell with about 5,000 images at 8-bit and 256 pixels x 256 pixels, at a frame rate of 25 fps. Then, move the z-axis position 2 µm down or up to obtain a defocused image for the chosen cell. Repeat the parameters to create a movie for this situation.
- Finally, without changing the z-axis position, search for a region without cells to repeat the same procedure and create a movie of the image background.
- Move the piezoelectric stage in the xy direction using the software to search for an isolated cell attached to the coverslip. Trap and attach a polystyrene sphere of known diameter to the RBC surface. Using the piezoelectric stage, slightly move the trapped bead, also attached to the RBC surface, in order to deform the cell, and then attach the bead to the coverslip.
- Contrast image acquisition
- Convert each of the three movies into three average images. Using ImageJ, select one of the movies, click on Image > Stacks > Z Project and choose the Average Intensity option. Repeat this procedure for the other movies to obtain their respective images.
- Change all the obtained images from 8-bits to float point 32-bits. Using ImageJ, click on Image > Type > 32-bits. Then, click on Analyze > Set Measurements and choose the Mean Gray Value option. Finally, click again on Analyze > Measure.
- Next, click on Process > Image Calculator and divide the focused image by the background image. To this result, multiply the average value of the gray level of the focused image. Obtain the average value by clicking on Process > Math > Multiply.
- To obtain the average value, choose the focused image, and then click on Analyze > Measure. For the representative image, the average value of the gray level is 69,199. Repeat the above procedures for the defocused image. In this case, the average value of the gray level is 69,231. Figure 5 shows the focused and defocused images before and after the procedure.
- Images may lose visual contrast during operations. To better visualize the images, click on Image > Adjust > Brightness/Contrast and select the Auto option.
- Next, to find the image contrast, use the following relationship:
 , where NImg is the gray level of the cell, N0 is the gray level outside the cell, and is a constant parameter corresponding to the gray level for zero light intensity that depends on the camera.
, where NImg is the gray level of the cell, N0 is the gray level outside the cell, and is a constant parameter corresponding to the gray level for zero light intensity that depends on the camera. - To find the value B, use a power meter to measure the light intensity. For each value of light intensity, a video must be recorded; thus, different intensity values can be related to different levels of gray. Finally, obtain a linear fit and relate B to the zero light intensity15.
- Find the value of N0, click on Polygon Selection icon and draw a polygon such as the one in Figure 6. Then, click on the Analyze tab and select Measure to find the mean gray level for the selected area. Each image is formed by a set of pixels and each pixel has a certain gray level. The set of all gray levels due to all pixels that make up the image corresponds to NImg.
- Use the contrast equation to determine NImg - No and execute this by selecting Process > Math > Subtract. Divide the result by N0 - B. Finally, find the contrast for the focused (C0) and defocused image (C1).
- Obtaining the height profile
- In order to obtain the height profile, use the already described method13. In brief, use the Hartley transform (FHT) to obtain the RBC thickness. In ImageJ, click on Process > FFT > FFT Options, and then choose FHT.
- Subtract the images C0 and C1 in ImageJ using Process > Math > Subtract to obtain the image for the following procedure, C= C0 - C1.
- For image C, click on Process > FFT > FFT Options, and then choose FHT to perform the Hartley transform of the image. Then, divide by the spatial frequency q2 using the custom-made plugin DivideQ2. Click on Plugin > DivideQ2.
NOTE: The file DivideQ2.class must be copied in the plugins directory where the ImageJ is installed. The plugin is provided as a .class file (Supplementary File 1) to be included in the plugin folder of ImageJ. - Then, perform the inverse transform FHT using Process > FFT > FFT to obtain an image with a gray level proportional to the height of the cell.
- Finally, click on Process > Math > Multiply to multiply the resulting image using the following constant:
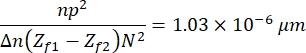
which is defined based on the characteristics of the images, the sample, and the experimental setup13. Here, n = 1.51 is the oil refractive index, p = 0.0721 μm is the relationship between micrometers and pixels of the images, Δn = 0.058 is the difference between the RBC and the aqueous medium refractive indices, the distance between the focusing and defocusing images (Zf1 - Zf2) = 2μm, and the size of the images, N2 = 256 pxl2. - Use the resulting image to obtain the height profile (Figure 7). The resulting image is used in ImageJ to observe different height profiles. It depends on where in the cell the yellow vertical line is placed, for example, in Figure 7 a height profile limited by the vertical line is obtained, observe this by pressing Ctrl + K.
- Form Factor
- After finding the image that contains the RBC height profile, use the 2 µm defocused contrast to create a set of two images in ImageJ. Click on Image > Stacks, and then select the option Images to Stack. To find the form factor, use an ImageJ customized macro to analyze the stack. The ImageJ customized macro is available for download as Supplementary File 2.
NOTE: The program uses the defocusing image to determine the cell edges. It then determines the perimeter, using the image that contains the height profile, for each horizontal position. In addition to the edges, it determines the perimeter, as well as the inverse of the perimeter. The sum of the inverse perimeter values, multiplied by the pixel thickness, corresponds to the inverse of the form factor. - Insert the pixel/micrometer relation in the program. Obtain this value from the microscope objective calibration experiment. In the example used, the value is 13.87 pixel/μm.
- Choose the horizontal starting position to put the yellow line in the first image of the stack. Start the line before the beginning of the cell and draw it beyond the vertical limits of the cell. In the example, the yellow line has 153 pixels of length and the initial position is between i = 70, y1 = 80 and i = 70, and y2 = 195. Then, move the yellow line horizontally until the final position is f = 245, y1 = 80 and f = 245, and y2 = 195.
- Finally, to find the cell edges, the perimeter, and the inverse of the perimeter, select the Macro tab and click on Run Macro. The macro will deliver a table with the edges position, the perimeter and the inverse of the perimeter, and an image of the analyzed cell. Check whether the edges of this image are similar to the edges of Figure 7, otherwise, repeat the procedure.
- Use the sum of the inverse of the perimeter to find the form factor8.
- After finding the image that contains the RBC height profile, use the 2 µm defocused contrast to create a set of two images in ImageJ. Click on Image > Stacks, and then select the option Images to Stack. To find the form factor, use an ImageJ customized macro to analyze the stack. The ImageJ customized macro is available for download as Supplementary File 2.
7. Soft glassy rheology model and experimental analysis
- Organizing the experimental data in a table
- Create a new table in the analysis software by clicking on the File tab. Determine 10 different columns (from c0 to c9) for the following parameters: angular frequencies used (rad/s): c0; K' (pN/µm) values obtained for each angular frequency: c1; ErrK': c2; K" (pN/µm) values obtained for each angular frequency: c3; ErrK": c4; G'(Pa) values obtained for each angular frequency: c5; ErrG': c6; G" (Pa) values obtained for each angular frequency: c7; ErrG": c8 and Ff with its respective error: c9 (Figure 8). Use the following formula to populate the following columns:
c5 = (3 x c1) / (8 x 1.28 x 0.087)
c6 = (3 / (8 x 0.087 x 1.28)) x sqrt (c2^2 + (c1 x 0.01 / 1.28)^2 + (c1 x 0.008 / 0.087) ^ 2)
c7 = (3 x c3) / (8 x 1.28 x 0.087)
c8 = (3 / (8 x 0.087 x c4)) x sqrt (c4^2 + (c3 x 0.01 / 1.28)^2 + (c3 x 0.008 / 0.087)^2)
- Create a new table in the analysis software by clicking on the File tab. Determine 10 different columns (from c0 to c9) for the following parameters: angular frequencies used (rad/s): c0; K' (pN/µm) values obtained for each angular frequency: c1; ErrK': c2; K" (pN/µm) values obtained for each angular frequency: c3; ErrK": c4; G'(Pa) values obtained for each angular frequency: c5; ErrG': c6; G" (Pa) values obtained for each angular frequency: c7; ErrG": c8 and Ff with its respective error: c9 (Figure 8). Use the following formula to populate the following columns:
- Plotting curve G' (ω) versus G" (ω)
- To generate the curve G' (ω) versus G" (ω) in the analysis software, use the data from the previous table. Click on Gallery > Linear and choose the Scatter Plot format.
- A new window will open. Select the G" column as the x-axis and the G' column as the y-axis. Finally, click on the Plot button to obtain the graph.
- To add the error bars in the plot, click on the Plot window, and then click on Plot > Error Bars. A new window will open. First, mark the Y Err option. Another window, called Error Bar Settings will open.
- Click on % of Value, select Data Column, and then click on the column ErrG'. Finally, click on OK > Plot, the error bars for the y-values will appear. Repeat the same procedure for x-axis values by now selecting the X Err square and the correct column for the ErrG".The final plot will be similar to the one shown in Figure 9.
- Fitting the parameters to the soft glassy rheology model
NOTE: The data analysis is divided into two parts: 1) curve fitting the G' (ω) versus G" (ω) plot to obtain the parameters Γ and Gm; 2) curve fitting G' (ω) and G" (ω) as a function of the frequency ω, to obtain the power law exponent α.- Curve fitting the G' (ω) versus G" (ω) plot to obtain the parameters Γ and Gm.
- Click on the Curve Fit tab, select Fit1. A new window will open. Select the Square and click on the Define button. A window called general curve fit definition will appear. Type the following equation:
m1 + m0/m2
where m1 = 61.576; m2 = 1, with allowable error of 1 x 10-5. Here m0 represents G", m1 represents Gm and m2 represents Γ.
NOTE: For m1 and m2 it is necessary to estimate their respective values during the curve fit definition. The estimations above were based on the example experiment shown. In the experiments, estimate the numbers according to the values observed in the plot. - Click on the OK button in both the windows and the fitting will appear, as shown in Figure 10 - a black curve. Check the correct values for m1 and m2, listed in the curve fit table that appeared with the plot.
- Click on the Curve Fit tab, select Fit1. A new window will open. Select the Square and click on the Define button. A window called general curve fit definition will appear. Type the following equation:
- Curve fitting G' and G" as a function of the angular frequency ω
- Next, create two other plots, namely, G' as a function of ω and G' as a function of ω. Place the error bars only on the y-axis, as previously demonstrated.
- Repeat the curve fitting procedure but now in the Curve Fit Selections, select G" option, and then in General Fit > Curve Definition, write the following equation:

In this case, m1 was estimated to be the value of G" (ω) = 23.683 Pa, when ω = 6.3 rad/s; m2 was estimated to be 0.5 (remember that m2 is the exponent α and varies between 0 and 1). Insert the value for Γ = 2.0293, according to the result of m2 in Figure 10. - Mark the option Weight Data. After all these procedures, click on OK, and a curve fitting similar to the one in Figure 11 - a blue curve will appear. The values for α, α = 0.63 ± 0.02 and G0, G0 = (3.7 ± 0.3)Pa will appear. Use these values to fit the next curve, G' (ω).
- Click on the next curve, repeat the curve-fitting procedure but now in the General Fit Curve Definition, write the following equation:

In this case, m3 is just an estimated value of α to confirm the previously obtained value. Use the values for G0 = 3.703 and G' (ω) = 23.683 Pa when ω = 6.3 rad/s. - Again, add 1 x 10-5 as allowable error and mark the option Weight Data. After all these procedures, click on OK, and a curve fitting similar to the one in Figure 11 - a green curve will appear.
- Curve fitting the G' (ω) versus G" (ω) plot to obtain the parameters Γ and Gm.
Results
Figure 1 represents the schematics of the OT system used for the rheology measurements. Figure 2 shows the schematics of the microrheology experiment with both spheres and a representative RBC is also shown. Figure 3 shows a typical curve for the amplitudes of both spheres as a function of time when the sinusoidal movements are produced by the piezoelectric stage. While the reference sphere (Figure 3 - red curve) oscillates following the stage movement, the RBC sphere (Figure 3 - a blue curve) oscillates with a different amplitude and phase. By measuring these parameters, it is possible to determine the complex elastic constant K* (ω) for different RBCs in the sample. Figure 4 shows a typical plot for the storage elastic constant K' (ω) as a function of the loss elastic constant K" (ω). The linear dependence observed demonstrates that the RBC surface can be considered a soft glassy material. Next, to obtain the overall cell form factor, Ff, a DM procedure is necessary and Figure 5, Figure 6, and Figure 7 include some of the required steps for the purpose. Then, to convert forces and deformations into stresses and strains, it is necessary to turn K* (ω) into G* (ω).
The complex RBC elastic constant is defined as K* (ω) = K' (ω) + iK" (ω). Moreover, K* (ω) is related to the RBC complex shear modulus G* (ω) = G' (ω) + iG" (ω). G' (ω) and G" (ω) are the RBC shear storage and loss moduli, respectively. The relation between K* (ω) and G* (ω) is given by:

where Ff is a form factor that depends on the RBC geometry, as previously mentioned, and ζ is the RBC membrane thickness, previously determined as ζ = (0.087 ± 0.009)μm8,15.
Furthermore, the storage G' (ω) and G" (ω) loss shear moduli are related, respectively, to the storage K' (ω) and loss K" (ω) elastic constants through the equations8,9
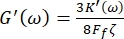 and
and 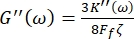
To find the standard errors for G' (ω) and G" (ω), Err G' and Err G", respectively, use the propagation of uncertainties equations with the results of K' (ω) and K" (ω), according to the following equations8,9:

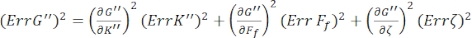 .
.
According to the soft glassy rheology theory, the RBCs behave like viscoelastic materials such as emulsions, pastes, and slurries8,9 and their storage and loss moduli obey the following equations:
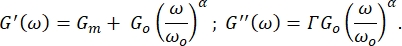
Thus,  , where Gm is the cell membrane shear modulus, G0 is the low frequency storage modulus, Γ is the ratio
, where Gm is the cell membrane shear modulus, G0 is the low frequency storage modulus, Γ is the ratio 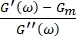 , α is the power-law exponent of soft glassy rheology model, and ω0 = 1 rad/s 8,9.
, α is the power-law exponent of soft glassy rheology model, and ω0 = 1 rad/s 8,9.
The values found for Ff and also the RBC surface thickness ζ were used (estimated at 87 ± 8 nm8,9,15). The results are shown in Figure 8, Figure 9, and Figure 10. Again, the linear dependency between G' and G" is in line with the hypothesis that RBC surfaces can be modeled as soft glassy materials. Also, from the linear fit of this plot, the value of Gm can be obtained, and by introducing this value to the soft glassy rheology curve fit of G", the values of G0 and α are determined (Figure 11 - a blue curve). Furthermore, after using the obtained result for G0 and adding it to the soft glassy rheology curve fit of G', the same value for the exponent is derived, within error bars (Figure 11 - a green curve).

Figure 1: Schematic representation of the OT microscope. The entire system is built upon an anti-vibration table. The laser is aligned using at least two different dichroic mirrors (white) and directed to the back entrance of the microscope objective lens using another dichroic mirror (light blue). A piezoelectric stage and a digital scientific camera attached to a computer are also necessary. Please click here to view a larger version of this figure.
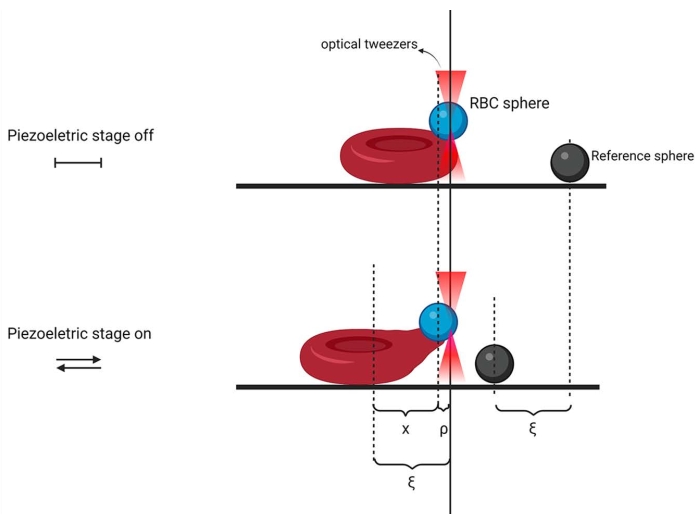
Figure 2: Schematics of the microrheology experiment. The reference sphere (dark gray) is attached to the coverslip and the RBC sphere (blue) is attached to the erythrocyte surface (red) and trapped by the OT (indicated by peach triangles when the laser is on). ρ is the equilibrium position of the RBC sphere in the trap; ξ is the sinusoidal movement of the sample and x is the cell deformation. The schematic image was created in Biorender. Please click here to view a larger version of this figure.
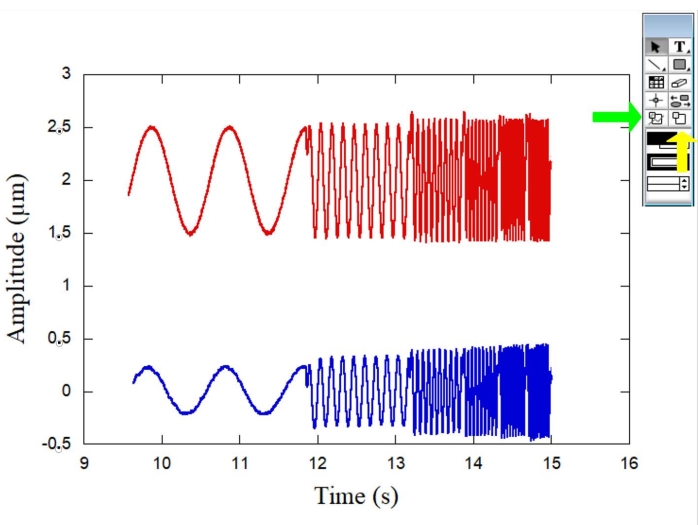
Figure 3: Plot illustrating the amplitudes (µm) of both spheres over time (s) when sinusoidal movements are produced by the piezoelectric stage. The reference sphere (red curve) oscillates following the stage movement, while the RBC sphere (blue curve) oscillates with a different amplitude and phase. The green arrow in the right indicates the data selection tool while the yellow arrow indicates the zoom selection tool. Please click here to view a larger version of this figure.

Figure 4: RBC microrheology results. Store elastic constant as a function of loss elastic constant for different RBCs in the sample (n = 10 different cells from three different samples). Data points represent the mean values of both K' (y-axis) and K" (x-axis) with their respective error bars (standard error of mean), obtained for each angular frequency used in the experimental setup. Please click here to view a larger version of this figure.
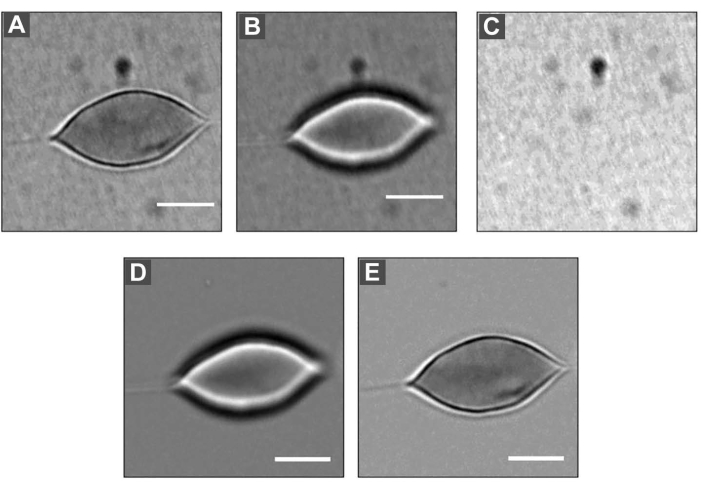
Figure 5: DM applied to an RBC. (A) Defocused image, size = 2 µm. (B) Image in focus. (C) Background image. Dividing each image (A) and (B) by the background image (C), and then multiplying by the average gray value of each image, it is possible to obtain images (D) and (E). Scale bar: 5 µm. Please click here to view a larger version of this figure.
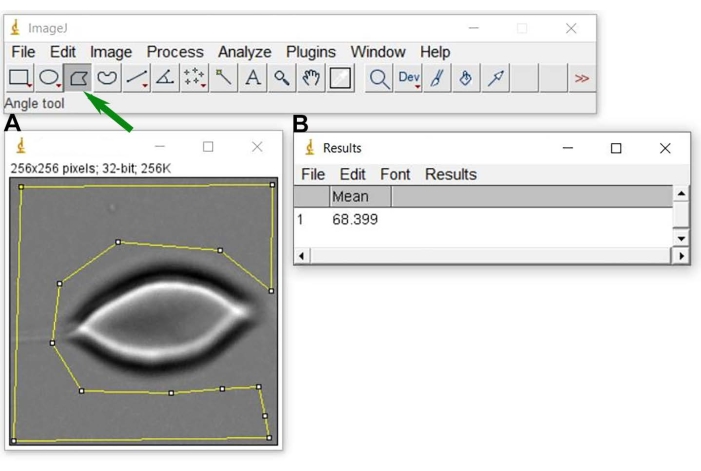
Figure 6: Background gray level N0. After opening the representative image in ImageJ (A), select a region (yellow geometric figure around the RBC cell) used to obtain the mean value of the background gray level and the result (B). To perform the yellow selection in A, use the polygon selection tool of Image J (indicated with a green arrow). Please click here to view a larger version of this figure.

Figure 7: Height profile for the deformed RBC. Height profile (left) represented along the vertical yellow line of the image (right). Please click here to view a larger version of this figure.

Figure 8: Representative screenshot of a typical table of results in the analysis software. Please click here to view a larger version of this figure.

Figure 9: RBC viscoelastic parameters. Store shear modulus as a function of the loss shear modulus for different RBCs in the sample (n = 10 different cells from three different samples). Data points represent the mean values of both, G' (y-axis) and G" (x-axis), with their respective error bars (standard error of mean), obtained for each angular frequency used in the experiments. Please click here to view a larger version of this figure.

Figure 10: Curve fit of G' (Pa) as a function of G" (Pa). The linear black line is the curve fit for the data points. N = 10 different cells from three different samples. Error bars represent the standard error of mean. Please click here to view a larger version of this figure.
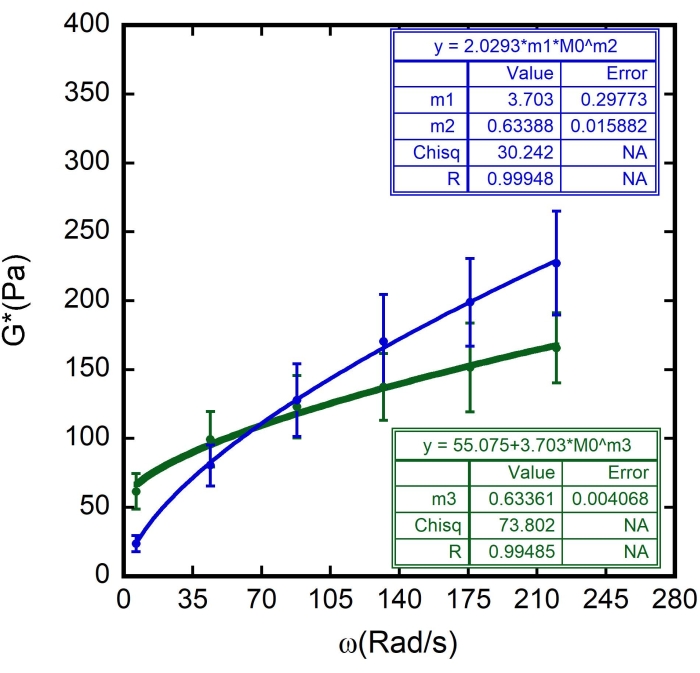
Figure 11: Adjusting the soft glassy rheology model to the results. The complex shear modulus (G*) as a function of the angular frequency ω for different RBCs in the sample. The green circles in the plot represent the mean values of G', while the blue circles represent the mean values of G", plotted with their respective error bars. The continuous green and blue lines represent the curve fittings for the soft glassy rheology model. The parameters m1, m2 and m3 are indicated in the plot. While m1 is G0, m2 and m3 are the exponent, α. N = 10 different cells from three different samples. Error bars represent the standard error of mean. Please click here to view a larger version of this figure.
Supplementary File 1: ImageJ plugin DivideQ2.class. Please click here to download this File.
Supplementary File 2: ImageJ customized macro to obtain the form factor. Please click here to download this File.
Discussion
In this protocol, an integrated method based on optical tweezers and defocusing microscopy is presented to quantitatively map the viscoelastic properties of RBCs. Results for the storage and loss shear moduli, together with the scaling exponent that characterizes the soft glassy rheology of RBC are determined. Application of this protocol for different experimental conditions, such as in physiological situation8 or along each stage of P. falciparum intra-erythrocytic cycle9 has already been carried out.
References in the literature point to discrepancies in RBC rheology, partially attributed to changes in cell morphology not properly taken into account during measurements6,7. Using dynamic light scattering, values for the RBC storage and loss moduli were reported ranging from 0.01-1 Pa, in the frequency range of 1-100 Hz6. In another study, using optical magnetic twisting cytometry, the apparent complex elastic modulus was determined7, but diverged from the dynamic light scattering values; thus, a multiplicative factor of 84 was used for comparative purposes. Following the procedures described in the present protocol, these differences were clarified8 by characterizing the RBC form factor using a noninvasive defocusing microscopy technique11,12,13. The complex shear modulus, that characterizes cell surfaces, can be obtained only if the geometry is considered16,17 and this was not always properly performed.
The integrated methodology presented in this protocol allows performing both methods (OT measurement and DM measurement) for the same single cell, one after the other. It also allows to perform OT measurements for different cells in a population, and then perform DM measurements for other cells in the same cell population. The last option will probably introduce more variability to both results but the errors can be propagated accordingly, in such a way that the results will correlate the overall RBC morphology with the overall RBC viscoelastic properties in a given population of cells corresponding to a particular experimental condition.
The main limitation for executing this protocol is the intrinsic difficulty in performing the method itself since it is an integration of optical tweezers and defocusing microscopy; thus, the availability of instruments to perform all the steps described can be a challenge. However, if one has access to an OT facility, it is much more feasible to eventually adapt the facility to perform the experiments. That is where the present protocol fits in, not only detailing every step to perform the measurements and analysis but also helping people to identify and adopt these OT systems instead of creating a setup from scratch.
Also, RBC attachment to coverslips becomes a limiting factor since they are non-adherent cells and such steps can introduce difficulties in measurements, as some RBCs may be detached. Thus, it is important to choose a well-adhered RBC. One way to check whether the choice was successful can occur at the time of preparing the sample for the measurement. After positioning the OT-trapped RBC sphere to the cell surface, slightly move the sample to ensure that the cell is firmly fixed and has not changed position following the OT-trapped bead. If so, look for another cell in the sample. Future improvements such as the use of dual-beam OT to simultaneously trap the RBC and perform the rheology measurements at the same time can also be done.
Apart from that, the possibility to extract single cell-based quantitative viscoelastic information of RBCs enables a variety of applications that are just beginning to be explored8,9. Thus, the presented method can be extended to the characterization of RBC mechanical behavior under other physio-pathological conditions like iron deficiency anemia and diabetes or in genetic blood diseases such as sickle cell disease and thalassemia, for example. Such an integrated tool may provide the basis for the development of novel diagnostic methods capable of correlating the changes in RBC viscoelastic properties with modifications in the blood flow of individuals with different pathologies.
Disclosures
The authors have no financial interests in the products described in this manuscript and have nothing else to disclose.
Acknowledgements
The authors would like to acknowledge all the members of CENABIO advanced microscopy facility for all-important help. This work was supported by the Brazilian agencies Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq), Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES) - Financial Code 001, Fundação de Amparo à Pesquisa do Estado do Rio de Janeiro (FAPERJ), and Instituto Nacional de Ciência e Tecnologia de Fluidos Complexos (INCT-FCx) together with Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP). B.P. was supported by a JCNE grant from FAPERJ.
Materials
| Name | Company | Catalog Number | Comments |
| 35mm culture dishes | Corning | 430165 | |
| Bovine serum albumin | Sigma-Aldrich | A9418 | |
| Coverslips | Knittel Glass | VD12460Y1A.01 and VD12432Y1A.01 | |
| Glass-bottom dishes | MatTek Life Sciences | P35G-0-10-C | |
| Glucose | Sigma-Aldrich | G7021 | |
| ImageJ | NIH | https://imagej.nih.gov/ij/ | |
| Immersion oil | Nikon | MXA22165 | |
| Inverted microscope | Nikon | Eclipse TE300 | |
| KaleidaGraph | Synergy Software | https://www.synergy.com/ | |
| KCl | Sigma-Aldrich | P5405 | |
| KH2PO4 | Sigma-Aldrich | P5655 | |
| Microscope camera | Hamamatsu | C11440-10C | |
| Na2HPO4 | Sigma-Aldrich | S5136 | |
| NaCl | Sigma-Aldrich | S5886 | |
| Neubauer chamber | Sigma-Aldrich | BR717805-1EA | |
| Objective lens | Nikon | PLAN APO 100X 1.4 NA DIC H; PLAN APO 60x 1.4 NA DIC H and Plan APO 10x XXNA PH2 | |
| Optical table | Thorlabs | T1020CK | |
| OT laser | IPG Photonics | YLR-5-1064-LP | |
| Polystyrene microspheres | Polysciences | 17134-15 | |
| rubber ring | Forever Seals | NBR O-Ring | |
| Silicone grease | Dow Corning | Z273554 | |
| Stage positioning | PI | P-545.3R8S | |
| Pipette | Gilson | P1000 |
References
- Fowler, V. M. The human erythrocyte plasma membrane: a Rosetta Stone for decoding membrane-cytoskeleton structure. Current Topics in Membranes. 72, 39-88 (2013).
- Tomaiuolo, G. Biomechanical properties of red blood cells in health and disease towards microfluidics. Biomicrofluidics. 8 (5), 051501 (2014).
- Depond, M., Henry, B., Buffet, P., Ndour, P. A. Methods to investigate the deformability of RBC during malaria. Frontiers in Physiology. 10, 1613 (2019).
- Boal, D. . Mechanics of the Cell. 2 edn. , (2012).
- Balland, M., et al. Power laws in microrheology experiments on living cells: Comparative analysis and modeling. Physical Review E. 74 (2), 021911 (2006).
- Amin, M. S., et al. Microrheology of red blood cell membranes using dynamic scattering microscopy. Optics Express. 15 (25), 17001-17009 (2007).
- Puig-de-Morales-Marinkovic, M., Turner, K. T., Butler, J. P., Fredberg, J. J., Suresh, S. Viscoelasticity of the human red blood cell. American Journal of Physiology Cell Physiology. 293 (2), 597-605 (2007).
- Gomez, F., et al. Effect of cell geometry in the evaluation of erythrocyte viscoelastic properties. Physical Review E. 101 (6-1), 062403 (2020).
- Gomez, F., et al. Plasmodium falciparum maturation across the intra-erythrocytic cycle shifts the soft glassy viscoelastic properties of red blood cells from a liquid-like towards a solid-like behavior. Experimental Cell Research. 397 (2), 112370 (2020).
- Pompeu, P., et al. Protocol to measure the membrane tension and bending modulus of cells using optical tweezers and scanning electron microscopy. STAR Protocols. 2 (1), 100283 (2021).
- Agero, U., Mesquita, L. G., Neves, B. R., Gazzinelli, R. T., Mesquita, O. N. Defocusing microscopy. Microscopy Research and Technique. 65 (3), 159-165 (2004).
- Agero, U., Monken, C. H., Ropert, C., Gazzinelli, R. T., Mesquita, O. N. Cell surface fluctuations studied with defocusing microscopy. Physical Review E. 67 (5), 051904 (2003).
- Roma, P. M. S., Siman, L., Amaral, F. T., Agero, U., Mesquita, O. N. Total three-dimensional imaging of phase objects using defocusing microscopy: Application to red blood cells. Applied Physics Letters. 104 (25), 251107 (2014).
- Köhler, A. New method of illumination for photomicrographical purposes. Journal of the Royal Microscopical Society. 14, 261-262 (1894).
- Nans, A., Mohandas, N., Stokes, D. L. Native ultrastructure of the red cell cytoskeleton by cryo-electron tomography. Biophysical Journal. 101 (10), 2341-2350 (2011).
- Ayala, Y. A., et al. Rheological properties of cells measured by optical tweezers. BMC Biophysics. 9, 5 (2016).
- Ayala, Y. A., et al. Effects of cytoskeletal drugs on actin cortex elasticity. Experimental Cell Research. 351 (2), 173-181 (2017).
Reprints and Permissions
Request permission to reuse the text or figures of this JoVE article
Request PermissionThis article has been published
Video Coming Soon
Copyright © 2025 MyJoVE Corporation. All rights reserved
We use cookies to enhance your experience on our website.
By continuing to use our website or clicking “Continue”, you are agreeing to accept our cookies.
