Anemometria a temperatura costante: uno strumento per studiare il flusso turbolento dello strato limite

Fonte: Xiaofeng Liu, Jose Roberto Moreto e Jaime Dorado, Dipartimento di Ingegneria Aerospaziale, San Diego State University, San Diego, California

Uno strato limite è una sottile regione di flusso immediatamente adiacente alla superficie di un corpo solido immerso nel campo di flusso. In questa regione, gli effetti viscosi, come lo stress da taglio viscoso, dominano e il flusso è ritardato a causa dell'influenza dell'attrito tra il fluido e la superficie solida. Al di fuori dello strato limite, il flusso è inviscido, cioè non ci sono effetti dissipativi dovuti all'attrito, alla conduzione termica o alla diffusione di massa.

Il concetto di strato limite fu introdotto da Ludwig Prandtl nel 1904, che consente una significativa semplificazione dell'equazione di Navier-Stokes (NS) per il trattamento del flusso su un corpo solido. All'interno dello strato limite, l'equazione NS è ridotta all'equazione dello strato limite, mentre al di fuori dello strato limite, il flusso può essere descritto dall'equazione di Eulero, che è una versione semplificata dell'equazione NS.

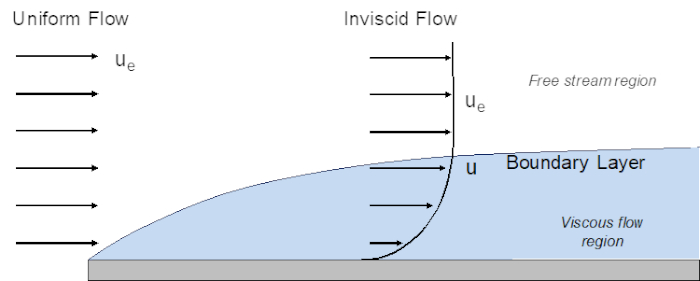
Figura 1. Sviluppo dello strato limite su una piastra piana.

Il caso più semplice per lo sviluppo dello strato limite si verifica su una piastra piana con angolo di incidenza zero. Quando si considera lo sviluppo dello strato limite su una piastra piana, la velocità al di fuori dello strato limite è costante in modo che il gradiente di pressione lungo la parete sia considerato pari a zero.

Lo strato limite, che si sviluppa naturalmente su una superficie corporea solida, subisce tipicamente le seguenti fasi: in primo luogo, lo stato dello strato limite laminare; in secondo luogo, lo stato di transizione e in terzo luogo, lo stato turbolento dello strato limite. Ogni stato ha la propria legge (s) che descrive la struttura del flusso dello strato limite.

La ricerca sullo sviluppo e la struttura dello strato limite è di grande importanza sia per lo studio teorico che per le applicazioni pratiche. Ad esempio, la teoria dello strato limite è la base per calcolare la resistenza all'attrito della pelle su navi, aerei e pale di turbomacchine. La resistenza all'attrito cutaneo si crea sulla superficie corporea all'interno dello strato limite ed è dovuta allo sforzo di taglio viscoso esercitato sulla superficie attraverso particelle fluide a diretto contatto con esso. L'attrito cutaneo è proporzionale alla viscosità del fluido e al gradiente di velocità locale sulla superficie nella direzione normale della superficie. La resistenza all'attrito della pelle è presente su tutta la superficie, quindi diventa significativa su vaste aree, come l'ala di un aeroplano. Inoltre, il flusso di fluido turbolento crea una maggiore resistenza all'attrito della pelle. Il moto del fluido macro-turbolento migliora il trasferimento del momento all'interno dello strato limite portando particelle fluide con elevata quantità di moto verso la superficie.

Questa dimostrazione si concentra sullo strato limite turbolento su una piastra piana, in cui il flusso è irregolare, come nella miscelazione o nell'eddying, e le fluttuazioni sono sovrapposte al flusso medio. Quindi, la velocità in qualsiasi punto di uno strato limite turbolento è una funzione del tempo. In questa dimostrazione, l'anemometria a filo caldo a temperatura costante, o CTA, verrà utilizzata per condurre un'indagine a livello limite. Quindi, il metodo del grafico di Clauser verrà utilizzato per calcolare il coefficiente di attrito della pelle in uno strato limite turbolento.

Un flusso turbolento è quello in cui fluttuazioni irregolari, come movimenti di miscelazione o di eddying, sono sovrapposti al flusso medio. La velocità in qualsiasi punto di uno strato limite turbolento è una funzione del tempo. Le fluttuazioni possono verificarsi in qualsiasi direzione del campo di flusso e influenzano i grumi macroscopici di fluido. Pertanto, mentre il trasporto della quantità di moto avviene su scala microscopica (o molecolare) in uno strato limite laminare, si verifica su scala macroscopica in uno strato limite turbolento. La dimensione di questi grumi macroscopici determina la scala della turbolenza.

Gli effetti causati dalle fluttuazioni sono come se la viscosità fosse aumentata. Di conseguenza, le forze di taglio alla parete e la componente di attrito cutaneo della resistenza sono molto più grandi quando lo strato limite è turbolento. Tuttavia, poiché uno strato limite turbolento può negoziare un gradiente di pressione avverso per una distanza più lunga, la separazione dello strato limite può essere ritardata o addirittura evitata del tutto.

Quando si descrive un flusso turbolento, è conveniente esprimere le componenti della velocità locale come la somma di un moto medio più un moto fluttuante:

dove è il valore medio temporale della componente u della velocità e 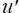è la velocità della fluttuazione. Il valore medio temporale in un dato punto dello spazio viene calcolato come:

L'intervallo di integrazione, Δt, dovrebbe essere molto più grande di qualsiasi periodo significativo della velocità di 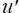fluttuazione, in modo da convergere verso un valore di velocità media. Quindi, per definizione, il valore medio convergente è indipendente dal tempo, cioè .

Per uno strato limite su una piastra piana, la velocità esterna 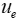è una costante. Pertanto il termine del gradiente di pressione è zero. Anche con questa semplificazione, non esiste una soluzione esatta per uno strato limite turbolento. Tuttavia, attraverso ampie indagini sperimentali e analitiche sullo strato limite, sono state stabilite la struttura del flusso e le relazioni empiricamente determinate che descrivono il profilo della componente tangenziale della velocità media.

Molto vicino al muro, domina la cesoia viscosa. Ad un primo ordine, il profilo di velocità è lineare; cioè, è proporzionale a y. Pertanto, lo sforzo di taglio della parete può essere espresso come:

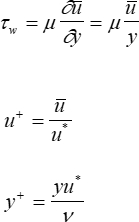
dove 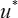è chiamata velocità di attrito cutaneo ed è definita come:

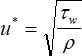
dove τ_w è l'attrito cutaneo, cioè lo sforzo di taglio della parete. L'attrito cutaneo è solitamente espresso in termini di coefficiente di attrito cutaneo, C_f, che è definito come:

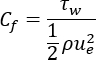
Con queste definizioni, è chiaro che per il sottostrato laminare, è valida la seguente relazione:

Nel sottostrato laminare, la velocità è così piccola che dominano le forze viscose e non c'è turbolenza. Il bordo del sottostrato laminare corrisponde a un y⁺ da 5 a 10.

Nel 1933, Prandtl dedusse che la velocità media nella regione interna dello strato limite doveva dipendere dallo sforzo di taglio della parete, cioè dall'attrito della pelle, dalle proprietà fisiche del fluido e dalla distanza, y, dalla parete. La velocità nella regione interna è quindi descritta dalla legge logaritrica del muro:

Nel 1930, Von Kármán dedusse che nella regione esterna dello strato limite turbolento, la velocità media, , è ridotta al di sotto del valore del flusso libero, 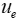, in un modo che è indipendente dalla viscosità ma dipende dallo sforzo di taglio della parete e dalla distanza, y, su cui il suo effetto si è diffuso. La velocità nella regione esterna è data da:

che è conosciuta come Legge della Scia. In questa equazione, 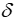è lo spessore dello strato limite, e 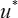è la velocità di attrito della pelle, che è definita come:

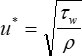
Per il flusso incomprimibile oltre una piastra piana, le costanti sono definite come segue:

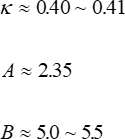
Una tecnica adatta per misurare le proprietà dello strato limite turbolento è l'anemometria a filo caldo, che si basa su due principi relativi all'effetto di raffreddamento del flusso su un filo riscaldato. Il primo principio si basa sul trasferimento di calore di un flusso su una superficie. Quando un fluido scorre su una superficie calda, il coefficiente di calore convettivo cambia, il che a sua volta influisce sul tasso di scambio termico su quella superficie e, di conseguenza, può influenzare ulteriormente la temperatura superficiale.

Il secondo principio è la legge di Joule, che afferma che la dissipazione del calore da un conduttore elettrico è proporzionale al potenziale elettrico che viene applicato al conduttore elettrico, al quadrato come mostrato nella seguente equazione:

dove è il flusso di calore, I è la corrente elettrica attraverso un conduttore, R è la resistenza elettrica del conduttore e U è il potenziale elettrico. Si possono usare questi due principi per correlare la velocità del flusso del fluido che circonda una sonda a filo metallico riscaldata misurando il potenziale elettrico applicato ai terminali della sonda. Il potenziale applicato può essere utilizzato per mantenere una corrente costante attraverso il filo, che è anemometria a corrente costante o CCA, o una temperatura costante sul filo, che è anemometria a temperatura costante o CTA.

In questa dimostrazione, utilizziamo l'anemometria a temperatura costante (CTA) per condurre un'indagine turbolenta dello strato limite. CTA è una tecnica diagnostica di flusso convenzionale ampiamente utilizzata che ha una risposta ad alta frequenza e può misurare le piccole scale di turbolenza senza grandi interferenze. La tecnica CTA utilizza un filo metallico molto sottile (≈ 5 μm, di solito fatto di platino o tungsteno), che è collegato a un braccio di un ponte di Wheatstone (Figura 2). Il filo viene riscaldato a una temperatura costante applicando una corrente elettrica. Qualsiasi raffreddamento è causato dal flusso di fluido attorno al filo. Il ponte di Wheatstone controlla il potenziale elettrico applicato al filo in risposta alle variazioni di velocità del flusso in modo che la resistenza del filo riscaldato, e quindi la temperatura del filo, sia mantenuta costante. La variazione del potenziale elettrico del ponte di Wheatstone definisce l'uscita del segnale del CTA.

Pertanto, la variazione del potenziale del ponte è una funzione del coefficiente di scambio termico, dove il coefficiente di trasferimento del calore è una funzione della velocità. Possiamo ottenere una correlazione empirica tra la velocità dell'aria e il potenziale elettrico del ponte calibrando sperimentalmente l'apparato a filo caldo. Ciò comporta l'adattamento dei dati sperimentali utilizzando relazioni di trasferimento di calore note.

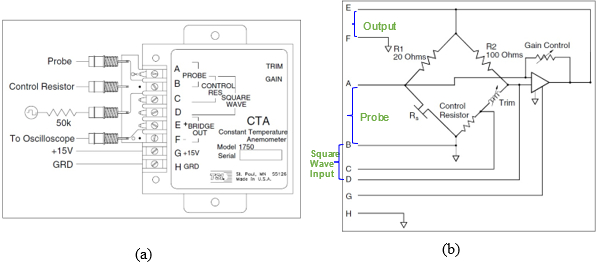
Figura 2. Anemometro a temperatura costante TSI modello 1750. a) Connettori per anemometri e cavi. b) Schema elettrico, in cui Rs rappresenta la sonda a filo caldo.

Una volta calcolata la velocità dell'aria utilizzando CTA, possiamo dedurre il coefficiente di attrito della pelle, C_f, sulla piastra piana. Sfortunatamente, la misurazione diretta della resistenza all'attrito cutaneo non è disponibile, pertanto vengono utilizzati metodi indiretti per determinarne il valore. Il metodo Clauser Chart è uno di questi metodi. Nel metodo del grafico di Clauser, il valore misurato del coefficiente di attrito cutaneo, C_f, è determinato confrontando il profilo di velocità dello strato limite misurato con una famiglia di curve derivate dalla legge logaritrica della parete con valori prescritti di coefficiente di attrito cutaneo. La curva che meglio si sovrappone alla porzione della legge logaritmo del profilo di velocità misurato sui grafici semi-log fornisce il valore del coefficiente di attrito cutaneo misurato.

1. Determinazione della risposta dinamica del sistema a filo caldo

Lo scopo di questa procedura è capire quanto velocemente il sistema anemometro può rispondere alle variazioni del segnale di flusso. Questa capacità viene misurata misurando la risposta in frequenza quando il segnale si accende e si spegne applicando un'onda quadra.

1. Fissare la sonda a filo caldo del sistema CTA all'interno di una galleria del vento utilizzando un albero di supporto.
2. Impostare un alimentatore CC, un generatore di segnali e un oscilloscopio e collegarli come mostrato nella Figura 2 (a). Il generatore di segnale fornisce un ingresso a onda quadra al ponte di Wheatstone e la forma d'onda di uscita viene visualizzata sull'oscilloscopio.
3. Accendere l'alimentatore a filo caldo, l'oscilloscopio e il generatore di segnali.
4. Impostare il generatore di segnale per emettere un'onda quadra con ampiezza di 150 mV e frequenza di 10 kHz.
5. Osservare il segnale di uscita nell'oscilloscopio per assicurarsi che la frequenza e l'ampiezza della forma d'onda in uscita siano corrette.
6. Chiudere la sezione di test e collegare la porta seriale. Accendi la galleria del vento e imposta la velocità dell'aria a 40 mph.
7. Una volta che il flusso d'aria si stabilizza, misurare la larghezza del segnale overshoot, τ, dall'oscilloscopio. Vedere la Figura 3 per la definizione di τ.
8. Utilizzare il valore misurato di τ per ottenere la frequenza di taglio del sistema a filo caldo utilizzando l'equazione: _{f cut} = 1/1.5τ.
9. Spegnere la galleria del vento.

2. Calibrazione del filo caldo

Lo scopo di questa procedura è stabilire la correlazione tra la velocità dell'aria e il potenziale elettrico del ponte di Wheatstone. Ciò consente di misurare la velocità del flusso.

1. Regolare la sonda a filo caldo in posizione verticale in modo che sia abbastanza lontana dalla piastra piana, che in questo caso è il pavimento della galleria del vento, in modo che si trovi nella regione del flusso libero.
2. Avviare il software di controllo della galleria del vento.
3. Aprire il software dello strumento virtuale e impostare la frequenza di campionamento su 10 kHz e il numero di campioni su 100.000. Questi parametri sono determinati dalle caratteristiche di flusso del campo di flusso da misurare e possono variare a seconda della conoscenza del requisito di convergenza delle statistiche mirate.
4. Imposta la velocità della galleria del vento a 0 mph e registra la tensione sul ponte di Wheatstone.
5. Aumentare la velocità dell'aria della galleria del vento con incrementi di 3 mph fino a 15 mph. Lasciare che il flusso si stabilizzi ad ogni velocità dell'aria prima di misurare la tensione.
6. Aumentare la velocità dell'aria della galleria del vento con incrementi di 5 mph fino a 60 mph e misurare la tensione ad ogni incremento.
7. Al termine di tutte le misurazioni, ridurre il flusso d'aria a 30 mph, quindi spegnere la galleria del vento.

Figura 3. Schema per la larghezza del superamento del segnale, τ come osservato su un oscilloscopio durante una prova ad onda quadra.

3. Rilievo dello strato limite

1. Utilizzando lo stesso set-up della sezione sperimentale precedente, abbassare lentamente la sonda a filo caldo fino a quando non tocca il pavimento della sezione di prova, che fungerà da piastra piana.
2. Accendi la galleria del vento e imposta la velocità dell'aria a 40 mph, la frequenza di campionamento a 10 kHz e il numero di campioni a 100.000 come in precedenza.
3. Registrare la lettura della tensione con l'impostazione verticale più bassa, che si trova accanto alla piastra piana e nello strato limite.
4. Spostare la sonda verticalmente, aumentando l'altezza a passi di 0,05 mm fino all'altezza di 0,50 mm e registrare la lettura della tensione in posizione verticale.
5. Aumentare l'altezza della sonda a passi di 0,10 mm fino all'altezza di 1,50 mm e registrare la lettura della tensione in posizione verticale.
6. Aumentare l'altezza della sonda a passi di 0,25 mm fino all'altezza finale di 4,00 mm e registrare la lettura della tensione in posizione verticale.
7. Al termine di tutte le misurazioni, ridurre la velocità dell'aria a 20 mph, quindi spegnere la galleria del vento, il CTA, l'alimentatore, l'oscilloscopio e il generatore di funzioni.

Il CTA è stato calibrato nella sezione 2 del protocollo misurando la tensione del filo caldo a diverse velocità dell'aria. Questi dati sono stati quindi utilizzati per determinare la relazione matematica tra la variabile misurata, la tensione, e la variabile indiretta, la velocità dell'aria. Esistono molti approcci per adattare i dati sperimentali alle relazioni matematiche per la velocità, molti dei quali sono trattati nell'appendice. Dopo aver determinato la relazione matematica, la velocità è facilmente calcolata dalla tensione in ulteriori esperimenti con il CTA.

Nella sezione 3 del protocollo, la velocità dell'aria è stata misurata utilizzando il CTA in diverse posizioni verticali nella galleria del vento. Questo rappresentava diverse distanze, y, dalla piastra piana. Dalla velocità del flusso istantaneo misurata in ciascun punto, è possibile ottenere il profilo di velocità media dello strato limite. Il profilo di velocità, u(y), può essere utilizzato per determinare la distanza verticale che la piastra dovrebbe essere spostata perpendicolarmente a se stessa per un flusso inviscido per ottenere la stessa portata che si verifica tra la superficie e il fluido, chiamata spessore di spostamento dello strato limite, 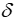*. Questo è definito come:

dove 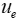è la velocità del flusso libero. Lo spessore del momento, θ, o la distanza che la piastra dovrebbe essere spostata nella direzione parallela a se stessa per avere la stessa quantità di moto che esiste tra il fluido e se stessa, è definita come:

Quindi, il fattore di forma, H, che può essere utilizzato per determinare la natura del flusso, è definito come:

dove un fattore di forma di 1,3 indica un flusso completamente turbolento, un fattore di forma di 2,6 indica il flusso laminare e qualsiasi valore intermedio rappresenta un flusso di transizione o turbolento ma non completamente sviluppato.

Per il caso dello strato limite turbolento, è possibile esaminare ulteriormente diverse proprietà. L'attrito cutaneo può essere determinato utilizzando il metodo del grafico clauser (vedere la Figura 4). Il metodo del grafico di Clauser può essere utilizzato per ottenere il coefficiente di attrito cutaneo, C_f, dalla velocità misurata, u(y). Dalla legge del registro del muro, abbiamo quanto segue:

dove κ ≈ 0,40 ~ 0,41 e B= da 5,0 a 5,5. In pratica, κ= 0,4 e B= 5,5. Dalla definizione, il coefficiente di attrito cutaneo è dato da:

dove q è la pressione dinamica del flusso libero e τ_w è la sollecitazione di taglio alla parete. La legge del tronco del muro può quindi essere espressa come (Vedi Appendice):

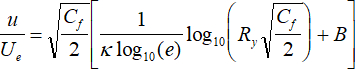
dove, .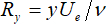

Data una serie di valori C_f, è possibile generare una famiglia di curve per vs. R_y. Diversi valori di R_y compresi tra 100 e 100.000 e C_f che vanno da 0,001 a 0,006 devono essere utilizzati per tracciare le curve in un formato log-lineare. Questo forma il grafico di Clauser, che può essere utilizzato per determinare il coefficiente di attrito della pelle, C_f, come mostrato nella Figura 4. Confrontando il profilo di velocità dello strato limite misurato con la famiglia di curve basate sulla legge di log della parete con i valori prescritti del coefficiente di attrito cutaneo, la curva che meglio si sovrappone alla porzione di legge logaritmica del profilo di velocità misurata fornisce il valore del coefficiente di attrito cutaneo misurato.

Figura 4: Grafico Clauser.

Questo risultato può essere confrontato con il risultato ottenuto utilizzando il metodo dell'equazione integrale. Inoltre, è possibile ottenere il profilo di fluttuazione della velocità e il risultato sperimentale può essere confrontato con la legge logaritria della parete. Per ulteriori informazioni, vedere l'Appendice.

La dimostrazione mostra come utilizzare l'anemometria a temperatura costante, un potente strumento utilizzato per studiare il flusso turbolento su una superficie, che in questo caso specifico era una piastra piana. Questo metodo è più semplice e meno costoso di altri metodi, come PIV, PTV e LDV, e fornisce un'alta risoluzione temporale. L'applicazione dell'anemometria a filo caldo a uno strato limite turbolento fornisce un approccio economico e pratico per dimostrare il comportamento dei flussi turbolenti.

L'anemometria a temperatura costante ha numerose applicazioni. Questa tecnica può essere utilizzata per rilevare sia flussi turbolenti che laminari. L'anemometria a filo caldo può essere utilizzata per studiare i flussi di scia di un profilo alare o di un modello di aeroplano, fornendo così informazioni come la resistenza del profilo alare e il livello di turbolenza di scia, che fornisce informazioni preziose per la progettazione di aeromobili.

L'anemometria a filo caldo può anche essere utilizzata in indagini di fluidodinamica ambientale, ad esempio per studiare i flussi di pennacchi, che sono responsabili del trasporto di massa e quantità di moto e della miscelazione di una varietà di processi presenti nell'atmosfera terrestre.

Una variante dell'anemometria a filo caldo è l'anemometria a film caldo, che viene tipicamente utilizzata nei flussi di liquidi che richiedono prestazioni robuste e affidabili. Ad esempio, il monitoraggio del flusso d'aria sul condotto di aspirazione dell'aria di un motore automobilistico viene spesso eseguito da un sensore fatto di pellicola calda.

L'applicazione dell'anemometria hotwire non è limitata al regno dell'ingegneria meccanica. Il CTA può anche essere utilizzato ad esempio in applicazioni biomediche per misurare la frequenza respiratoria.

Elenco dei materiali

Nome	Società	Numero di catalogo	Commenti
Attrezzatura
Galleria del vento subsonica didattica	Jetstream		Le dimensioni della sezione di prova della galleria del vento sono le seguenti: 5,25" (larghezza) x 5,25" (altezza) x 16" (lunghezza). La galleria del vento dovrebbe essere in grado di raggiungere velocità dell'aria di 0 - 80 mph.
Il Muro			La parete della sezione di prova è in vetro.
CTA modello 1750	TSI Corp.
Sonda a filo caldo	TSI Corp	STI 1218-T1.5	Sonda a strato limite standard rivestita in tungsteno-platino. Il diametro della sonda è di 3,81 μm. La lunghezza dell'area di rilevamento del filo è di 1,27 mm.
Scheda A/D	Strumenti nazionali	NI USB 6003	Frequenza di campionamento massima di 100 kHz con risoluzione a 16 bit
Sistema di traversata	Newport		Newport 370-RC Morsetto per barre rack e pignone e 75 assemblaggio di aste di supporto ottico smorzato
Tubo di Pitot			La pressione dinamica del flusso libero sarà percepita da un piccolo tubo di Pitot installato nella regione iniziale della sezione di prova. La risoluzione del tubo di Pitot è di 0,1 mph.
Software			Il software LabView verrà utilizzato per l'acquisizione dei dati.
Alimentatore	Landa	2718	Heath 2718 Tri-Power Supply con uscita 15V DC viene utilizzato per alimentare l'anemometro a filo caldo.
Oscilloscopio	Tektronix	2232
Generatore di segnali	Agilent	33110A