Méthode des sphères de turbulence : Évaluation de la qualité de l'écoulement en soufflerie
Vue d'ensemble
Source : Jose Roberto Moreto et Xiaofeng Liu, Department of Aerospace Engineering, San Diego State University, San Diego, CA
Les essais en soufflerie sont utiles dans la conception des véhicules et des structures soumis au flux d'air pendant leur utilisation. Les données de soufflerie sont générées par l'application d'un flux d'air contrôlé à un modèle de l'objet étudié. Le modèle d'essai a généralement une géométrie similaire, mais est une échelle plus petite par rapport à l'objet grandeur nature. Pour s'assurer que des données précises et utiles sont recueillies lors d'essais en soufflerie à basse vitesse, il doit y avoir une similitude dynamique du nombre Reynolds entre le champ d'écoulement du tunnel par rapport au modèle d'essai et le champ d'écoulement réel au-dessus de l'objet grandeur nature.
Dans cette démonstration, le flux de soufflerie sur une sphère lisse avec des caractéristiques de débit bien définies sera analysé. Étant donné que la sphère a des caractéristiques d'écoulement bien définies, le facteur de turbulence de la soufflerie, qui corrèle le nombre efficace de Reynolds au nombre de Reynolds d'essai, peut être déterminé, ainsi que l'intensité de turbulence en cours libre de la soufflerie.
Principles
Pour maintenir une similitude dynamique dans les flux à basse vitesse, le nombre de Reynolds d'une expérience doit être le même que le nombre Reynolds du phénomène de débit à l'étude. Cependant, les expériences effectuées dans différentes souffleries et en plein air, même au même nombre de Reynolds, pourraient donner des résultats différents. Ces différences peuvent être attribuées à l'effet de la turbulence en cours d'eau libre à l'intérieur de la section d'essai de la soufflerie, qui pourrait être perçue comme un « nombre de Reynolds efficace » plus élevé pour l'essai en soufflerie [1].
Une méthode simple qui est utilisée pour obtenir le nombre efficace de Reynolds pour une soufflerie et estimer son intensité de turbulence est l'utilisation de la sphère de turbulence. Cette méthode permet d'obtenir une mesure indirecte de l'intensité des turbulences en déterminant le facteur de turbulence de la soufflerie. Le facteur de turbulence, TF, corrèle le nombre efficace Reynolds, Reff, avec le numéro de tunnel Reynolds, Retest, comme
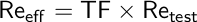
L'intensité de la turbulence peut être mesurée directement par une anémométrie de fil chaud, la vélocimétrie de Doppler de laser, ou le sondage de champ de velocimétrie d'image de particule. Avant l'introduction de ces méthodes de mesure directe, une sphère de turbulence était le principal moyen de mesurer la turbulence relative d'une soufflerie. Étant donné que les méthodes directes sont généralement longues et coûteuses, la méthode classique de la sphère de turbulence demeure une alternative rapide et peu coûteuse pour évaluer la qualité du débit d'air.
La méthode de la sphère de turbulence repose sur deux résultats empiriques : la crise de traînée de sphère et la forte corrélation entre le nombre critique de Reynolds, Rec, et l'intensité de turbulence de flux. La crise de traînée se réfère au phénomène que le coefficient de traînée de sphère, Cd, tombe soudainement en raison du décalage vers l'arrière du point de séparation de flux. Lorsque le flux atteint le nombre critique de Reynolds, la transition de la couche limite entre le débit laminaire et le flux turbulent se produit très près du bord d'attaque de la sphère. Cette transition précoce provoque une séparation d'écoulement retardée parce que la couche limite turbulente est mieux en mesure de négocier un gradient de pression défavorable sur une plus longue distance et est donc moins sujette à la séparation que la couche limite laminaire. La séparation retardée favorise une meilleure récupération de la pression, ce qui réduit la taille du sillage et la traînée de pression et diminue considérablement la traînée globale.
Les sphères de turbulence utilisées dans cette démonstration ont un robinet de pression au bord d'avant et quatre robinets de pression à des points situés à 22,5 degrés du bord de fuite. Trois sphères de diamètre de 4,0, 4,987 et 6,0 po, respectivement, seront étudiées. Pour une sphère lisse, le nombre critique de Reynolds est bien défini et se produit lorsque CD 0,3. Cela correspond à une valeur deP/q 1,220, où la différenceest la différence entre la pression moyenne mesurée aux quatre ports de pression arrière et la pression de stagnation à la sphère bord d'avant, et q est la dynamique de flux pression.
Bien que Rec soit bien défini par CD etP/q, il dépend fortement de la turbulence de débit. Cette démonstration à l'aide de sphères peut être utilisée pour définir le facteur de turbulence. Les premières mesures de vol ont révélé que dans l'atmosphère libre, Rec 3,85 x 105 pour une sphère lisse. L'air libre critique Reynolds est corrélé à la turbulence de la soufflerie par l'équation suivante:

Procédure
1. Préparation de la sphère de turbulence dans la soufflerie
- Connectez le tube pitot de la soufflerie au port #1 sur le scanner de pression, et connectez le port de pression statique au port #2 sur le scanner de pression.
- Verrouiller l'équilibre externe.
- Fixez la jambe de sphère au support d'équilibre à l'intérieur de la soufflerie.
- Installer la sphère avec 6 de diamètre.
- Connectez le robinet de pression de pointe au port #3 sur le scanner de pression, et connectez les quatre robinets de pression arrière au port #4 sur le scanner de pression.
- Fixez la ligne d'approvisionnement en air au régulateur de pression et régliez la pression à 65 psi.
- Connectez le collecteur du scanner de pression à la ligne de pression.
- Démarrer le système d'acquisition de données et le scanner de pression. Assurez-vous de les allumer au moins 20 minutes avant le test.
- Estimer la pression dynamique maximale basée sur le numéro critique
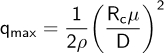 Reynolds en plein air pour une sphère lisse : . Voir les tableaux 1 et 2 pour les paramètres de test recommandés.
Reynolds en plein air pour une sphère lisse : . Voir les tableaux 1 et 2 pour les paramètres de test recommandés. - Définissez la plage de test de pression dynamique de 0 à qmax et définissez les points de test en divisant la plage en 15 intervalles.
Tableau 1. Paramètres pour le premier test.
| Diamètre de sphère (entre) | qMin [dans H2O] | qMax [dans H2O] |
| 4 | 4 | 6 |
| 4.987 | 2 | 3.4 |
| 6 | 1 | 2.4 |
Tableau 2. Paramètres pour le deuxième test.
| Diamètre de sphère (entre) | qMin [dans H2O] | qMax [dans H2O] |
| 4 | 3.4 | 7.2 |
| 4.987 | 1.3 | 5.1 |
| 6 | -- | -- |
2. Effectuer la stabilisation et la mesure de balayage de pression
- Lisez la pression barométrique et la température ambiante et enregistrez les valeurs.
- Appliquer les corrections à la pression barométrique à l'aide d'équations fournies par le fabricant de manomètres.
- Configurez le logiciel d'acquisition de données et connectez-le au scanner de pression, en définissant l'adresse IP appropriée.
- Insérez les commandes suivantes en appuyant sur entrez après chaque commande.
Le calz
Chan1 0
Chan 1-1.1-4
fps 10 - Vérifiez que la section d'essai et la soufflerie sont exemptes de débris.
- Fermez les portes de la section d'essai.
- Définir le cadran de vitesse de soufflerie à zéro.
- Allumez le système de refroidissement de la soufflerie et de la soufflerie.
- Avec la vitesse du vent à 0 mph, commencer à enregistrer les données, puis insérer la commande suivante pour scanner la pression:
-scan - Enregistrez la température de l'air en soufflerie.
- Augmentez la vitesse du vent jusqu'à la pression dynamique du point d'essai suivant telle que définie à l'étape 1.10.
- Attendez que la vitesse se stabilise, puis répétez les étapes 2.9 - 2.11 jusqu'à ce que le dernier point d'essai soit exécuté.
- Réduisez lentement la vitesse à zéro.
- Lorsque tous les points ont été mesurés, remplacez les 6 dans la sphère par la sphère suivante suivant les étapes 1.2 - 1.5.
- Répétez les étapes de 2.3 - 2.14 pour répéter les expériences de stabilisation et d'analyse de pression.
- Attendez que la soufflerie se refroidisse après l'exécution de l'essai pour les trois sphères.
- Éteignez la soufflerie et le logiciel d'acquisition de données.
Résultats
Pour chaque sphère, la pression de stagnation et la pression aux ports arrière ont été mesurées. La différence entre ces deux valeurs donne la différence de pression,P. La pression totale, Pt, et la pression statique, Ps, de la section de test ont également été mesurées, qui sont utilisées pour déterminer la pression dynamique de test, q - Pt - Ps, et la normalisée pression  . La pression de l'air ambiant, Pamb, et la température du débit d'air a également été enregistrée pour calculer les propriétés du débit d'air, y compris la densité de l'air, letestet la viscosité, letest. La densité est obtenue en utilisant la loi idéale sur le gaz, et la viscosité est obtenue en utilisant la formule de Sutherland. Une fois que la densité et la viscosité de l'air sont déterminées, le numéro Reynolds d'essai peut être calculé.
. La pression de l'air ambiant, Pamb, et la température du débit d'air a également été enregistrée pour calculer les propriétés du débit d'air, y compris la densité de l'air, letestet la viscosité, letest. La densité est obtenue en utilisant la loi idéale sur le gaz, et la viscosité est obtenue en utilisant la formule de Sutherland. Une fois que la densité et la viscosité de l'air sont déterminées, le numéro Reynolds d'essai peut être calculé.
En traçant le numéro Reynolds de test en ce qui concerne la différence de pression normalisée, le nombre critique de Reynolds pour chaque sphère a été déterminé (figure 1). Le nombre critique de Reynolds correspond à  une valeur de pression normalisée de 1,220. Les trois courbes pour les trois sphères fournissent une estimation plus précise du nombre critique de Reynolds,le tunnelRe C , parce qu'une valeur moyenne est utilisée. Avec l'estimation du tunnel ReC, le facteur de turbulence, TF, et le nombre efficace de Reynolds peuvent être déterminés selon les équations suivantes :
une valeur de pression normalisée de 1,220. Les trois courbes pour les trois sphères fournissent une estimation plus précise du nombre critique de Reynolds,le tunnelRe C , parce qu'une valeur moyenne est utilisée. Avec l'estimation du tunnel ReC, le facteur de turbulence, TF, et le nombre efficace de Reynolds peuvent être déterminés selon les équations suivantes :

et
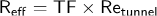
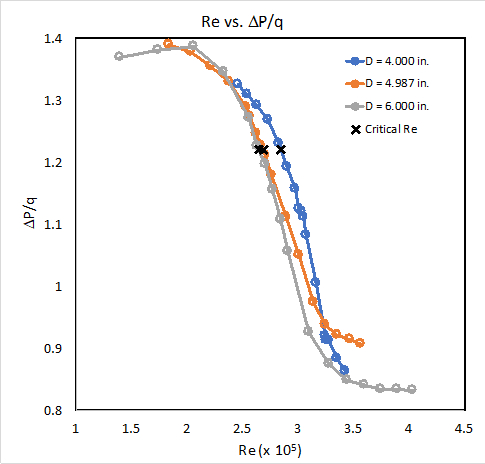
Figure 1. Numéro Reynolds critique pour chaque sphère.
Applications et Résumé
Les sphères de turbulence sont utilisées pour déterminer le facteur de turbulence en soufflerie et estimer l'intensité de la turbulence. Il s'agit d'une méthode très utile pour évaluer la qualité du débit d'une soufflerie parce qu'elle est simple et efficace. Cette méthode ne mesure pas directement la vitesse de l'air et les fluctuations de vitesse, telles que l'annémométrie des câbles chauds ou la vélocimétrie d'image de particules, et elle ne peut pas fournir une étude complète de la qualité du débit de la soufflerie. Cependant, un levé complet est extrêmement lourd et coûteux, de sorte qu'il n'est pas approprié pour des vérifications périodiques de l'intensité de la turbulence de la soufflerie.
Le facteur de turbulence peut être vérifié périodiquement, par exemple après avoir apporté des modifications mineures à la soufflerie, pour évaluer la qualité du débit. Ces vérifications rapides peuvent indiquer la nécessité d'une étude complète des turbulences d'écoulement. D'autres informations importantes obtenues à partir du facteur de turbulence sont le nombre efficace de Reynolds de la soufflerie. Cette correction sur le numéro Reynolds est importante pour assurer la similitude dynamique et l'utilité des données obtenues à partir de modèles à l'échelle et leur application à des objets à grande échelle.
Le principe de la sphère de turbulence peut également être utilisé pour estimer le niveau de turbulence dans d'autres environnements en plus de la section d'essai de soufflerie. Par exemple, cette méthode peut être utilisée pour mesurer la turbulence en vol. Une sonde de turbulence peut être développée sur la base des principes de la sphère de turbulence et installée dans les avions pour mesurer les niveaux de turbulence dans l'atmosphère en temps réel [2].
Une autre application est l'étude des structures de débit pendant un ouragan. Les mesures in situ du débit à l'intérieur d'un ouragan peuvent être extrêmement dangereuses et compliquées à obtenir. Des méthodes comme l'anémométrie des câbles chauds et la vélocimétrie d'image de particules sont inaccessibles dans ces conditions. Le principe de la sphère de turbulence peut être utilisé pour fabriquer un système de mesure dispendieux qui peut être placé dans une région sujette aux ouragans pour mesurer la turbulence d'écoulement à l'intérieur d'un ouragan en toute sécurité et à faible coût [3].
| nom | compagnie | Numéro de catalogue | Commentaires |
| équipement | |||
| Soufflerie à basse vitesse | Sdsu | Type de retour fermé avec des vitesses dans la gamme 0-180 mph | |
| Taille de section d'essai 45W-32H-67L pouces | |||
| Sphères lisses | Sdsu | Trois sphères, diamètres 4", 4.987", 6" | |
| Scanner de pression miniature | Scanivalve (Scanivalve) | ZOC33 (en) | |
| Module de service numérique | Scanivalve (Scanivalve) | DSM4000 (En) | |
| baromètre | |||
| Manomètre | Meriam Instrument Co. | 34FB8 (en) | Manomètre d'eau avec une portée de 10 po. |
| thermomètre |
References
- Barlow, Rae and Pope. Low speed wind tunnel testing, John Wiley & Sons, 1999.
- Crawford T.L. and Dobosy R.J. Boundary-Layer Meteorol. 1992. 59; 257-78.
- Eckman R.M., Dobosy R.J., Auble D.L., Strong T.W., and Crawford T.L. J. Atmos. Ocean. Technol. 2007; 24; 994-1007.
Tags
Passer à...
Vidéos de cette collection:

Now Playing
Méthode des sphères de turbulence : Évaluation de la qualité de l'écoulement en soufflerie
Aeronautical Engineering
8.7K Vues

Performances aérodynamiques d'un modèle réduit d'avion : Le DC-6B
Aeronautical Engineering
8.3K Vues

Caractérisation de l'hélice : Variations du pas, du diamètre et du nombre de lame sur la performance
Aeronautical Engineering
26.4K Vues

Comportement de l'aile : Distribution de la pression sur une aile de Clark Y-14
Aeronautical Engineering
21.1K Vues

Performance des ailes du Clark Y-14 : Déploiement des dispositifs hypersustentateurs (volets et lamelles)
Aeronautical Engineering
13.4K Vues

Flux cylindrique croisé : Mesurer la distribution de la pression et estimer les coefficients de traînée
Aeronautical Engineering
16.2K Vues

Variations du nombre de Mach et de la pression le long d'une tuyère convergente et d'une tuyère de Laval
Aeronautical Engineering
37.9K Vues

Imagerie Schlieren: Une technique pour visualiser les caractéristiques des écoulements supersoniques
Aeronautical Engineering
11.6K Vues

Visualisation de l'écoulement dans un tunnel hydrodynamique : Observation d'un tourbillon sur une aile Delta
Aeronautical Engineering
8.1K Vues

Visualisation de l'écoulement de colorants en surface : Une méthode qualitative pour visualiser les lignes de courant dans un écoulement supersonique
Aeronautical Engineering
4.9K Vues

Tube de Pitot : Un dispositif pour mesurer la vitesse du flux d'air
Aeronautical Engineering
49.0K Vues

Anémomètre à température constante : Un outil pour étudier les écoulements dans la couche limite turbulente
Aeronautical Engineering
7.2K Vues

Transducteur de pression : Calibrage à l'aide d'un tube de Pitot
Aeronautical Engineering
8.5K Vues

Contrôle de vol en temps réel : Étalonnage de capteurs embarqués et acquisition de données
Aeronautical Engineering
10.3K Vues

Aérodynamique des multicoptères : Caractérisation de la poussée sur un hexacoptère
Aeronautical Engineering
9.1K Vues