Method Article
Разлагая вариативность в чтение раскрыть уникальный и общие последствия языка и декодирование
В этой статье
Резюме
Здесь мы представляем протокол для разложения дисперсию прочитанного в уникальный и общие последствия языка и декодирования.
Аннотация
Простой вид чтения является популярная модель чтения, который утверждает, что чтение это продукт декодирования и языка, с каждым компонентом, однозначно прогнозировать прочитанного. Хотя исследователи утверждают, является ли сумма, вместо того, чтобы продукт компоненты самый лучший упредитель, не исследователи разделы дисперсии, объяснил для изучения степени, к которому компоненты доля дисперсии в прогнозировании чтения. Чтобы разложить дисперсии, мы вычитаем R2 для языка только модели от полной модели для получения уникальный R2 для декодирования. Во-вторых мы вычитаем R2 для декодирования только модели от полной модели для получения уникальный R2 для языка. В-третьих для получения общей дисперсии объясняется языка и декодирования, мы вычитаем сумму двух уникальных R2 от R2 для полной модели. Этот метод демонстрируется в регрессии подход с данными от студентов в классах 1 (n = 372), 6 (n = 309) и 10 (n = 122) с помощью наблюдаемых меру языка (восприимчивы словарь), декодирование (чтение приурочен слово) и понимание прочитанного (стандартизированный тест). Результаты свидетельствуют о сравнительно большое количество дисперсии прочитанного, объяснил в классе 1 общей вариативность декодирования и языка. В 10 классе однако, это уникальный эффект языка и общий эффект языка и декодирования объяснить большинство дисперсии прочитанного. Результаты обсуждаются в контексте расширенной версии простой вид чтения, что считает уникальным и общие эффекты языка и декодирование в прогнозировании прочитанного.
Введение
Простой вид чтения1 (SVR) продолжает, как популярная модель чтения из-за своей простоты чтения (R) является продуктом декодирования (D) и язык (L)- и потому что SVR стремится объяснить, в среднем, приблизительно 60% объяснил дисперсию в чтении 2понимание. SVR предсказывает, что корреляции между D и R будет сокращаться с течением времени и что корреляции между L и R будет увеличиваться со временем. Исследования в целом поддерживают это предсказание3,4,5. Существуют разногласия, однако, о функциональной форме СВР, с аддитивной модели (D + L = R) объясняя значительно больше дисперсия прочитанного чем модели продукции (D × L = R)6,7,8и сочетание суммы и продукта [R = D + L + (D × L) объясняя наибольшее количество вариативность в чтении понимание3,9.
Недавно в SVR модель распространилась за пределы на основе наблюдаемых переменных скрытых переменных моделирования с помощью подтверждающих фабрика анализа и моделирования структурных уравнение регрессии. D обычно измеряется с untimed или приурочен чтении реальные слова и/или nonwords и R обычно измеряется стандартизованной чтение тест, который включает грамотность и информационные проходы последовали тестовых вопросов. L обычно измеряется тесты восприимчивым и выразительный лексики и, особенно в начальных классах, мерами восприимчивым и выразительный синтаксиса и аудирование. Большинство продольных исследований сообщают, что L одномерного10,11,12,13. Однако еще лонгитюдное исследование14 сообщает структуру двух факторов для L в начальных классах и одномерного структуры в 4 и 8 классов. Последние Поперечные исследования сообщают, что лучшая модель bifactor подходит для данных и предсказывает R15,16,17,18. К примеру, Foorman и др. 16 по сравнению одномерного, три фактор, четыре фактор и bifactor модели SVR в данных от студентов в классах 4-10 и обнаружил, что модель bifactor лучше всего подходят и объяснил 72% до 99% дисперсии в р. Общий коэффициент L объяснил, что разница во всех семи классов и словарный запас и синтаксис однозначно объяснить расхождение только в одном классе. Хотя фактор D умеренно коррелировалось с L и R во всех классах (0,40-0,60 и 0,47-0,74, соответственно), он был однозначно не коррелирует с R при наличии общего коэффициента L.
Даже несмотря на то, что латентных переменных моделирования имеет расширенный SVR, проливают свет на размерность L и уникальную роль, которую играет L в прогнозировании R за пределами начальных классов, исследования не СВР за исключением одного, Foorman и др 19 разделы дисперсию прочитанного в то, что объясняется уникальным D и L и то, что является общим в общем. Это большое упущение в литературе. Концептуально это имеет смысл, что D и L будет делить вариативность в прогнозировании письменного языка, потому что слова признания влечет за собой лингвистических навыков фонологии, семантика и дискурса в предложении и тексте уровня20. Аналогичным образом лингвистическое осмысление должен быть подключен к ортогональных представлений фонемы, морфемы, слов, предложений и дискурса, если текст должен быть понятны21. Умножая D L не дают знания, разделяют эти компоненты. Только разложение дисперсии в то, что является уникальным и что разделяет D и L в прогнозирования R покажет интегрированных знаний, решающее значение для успеха образовательных мероприятий.
Одно исследование, Foorman и др. 19 , разложить дисперсию прочитанного в то, что является уникальным и что разделяют общие D и L занятых латентной переменной моделирования подход. Следующий протокол демонстрирует технику с данными от студентов в классах 1, 7 и 10, на основе единого наблюдается переменные D (приурочен декодирования), L (восприимчивы словарь), и R (стандартизированные чтения понимание тест) чтобы сделать процесс разложения легко понять. Данные представляют собой подмножество данных из Foorman и др. 19.
протокол
Примечание: Ниже шаги описывают разлагающихся общая вариативности в зависимой переменной (Y) в уникальный дисперсия, общей дисперсиии Необъяснимые расхождения компоненты, основанные на два отдельных независимых переменных (так называемый 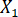 и
и  для этого примера) с использованием программного обеспечения с графическим интерфейсом пользователя и программное обеспечение управления данными (см. Таблицу материалы).
для этого примера) с использованием программного обеспечения с графическим интерфейсом пользователя и программное обеспечение управления данными (см. Таблицу материалы).
1. считывание данных в программное обеспечение с графическим интерфейсом пользователя
- Нажмите на файл.
- Наведите курсор мыши открытым.
- Нажмите на данных.
- Найдите файл соответствующих данных на компьютере.
- Если тип файла не согласуется с программного обеспечения с графическим интерфейсом пользователя, нажмите на Тип файлов и выберите файл, соответствующий формат.
- Нажмите на открытым.
2. Оцените дисперсию, объяснил в зависимой переменной (Y)
-
Общая дисперсия объяснил основанный на две независимые переменные — всего R2.
Примечание: Значение R2 известен как коэффициент детерминации и представляет собой долю дисперсии зависимой переменной, что объясняется набором независимых переменных.- Нажмите на анализ и наведите указатель мыши на регрессии и выберите линейных.
- Нажмите на зависимой переменной в список переменных. Затем нажмите на стрелку рядом с зависимыми.
- Нажмите на двух независимых переменных (X1 и X2) в списке переменная. Затем нажмите на стрелку рядом с Independent(s).
- Нажмите кнопку ОК.
- Нажмите на окно просмотра программного обеспечения.
- Используйте мышь для прокрутки в раздел под названием Сводка по модели. Запишите значение в столбце R квадрат и этикетки всего Rзначение2.
-
Всего объяснил дисперсию на основе
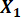
- Повторите шаги 2.1.1 через 2.1.4, используя только
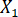 в списке независимой переменной.
в списке независимой переменной. - Нажмите на окно просмотра программного обеспечения.
- Используйте мышь для прокрутки в раздел под названием Сводка по модели. Запишите значение в столбце R квадрат и ярлык это значение
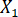 R2.
R2.
- Используйте мышь для прокрутки в раздел под названием Сводка по модели. Запишите значение в столбце R квадрат и ярлык это значение
- Повторите шаги 2.1.1 через 2.1.4, используя только
-
Всего объяснил дисперсию на основе

- Повторите шаги 2.1.1 через 2.1.4, используя только
 в списке независимой переменной.
в списке независимой переменной. - Нажмите на окно просмотра программного обеспечения.
- Используйте мышь для прокрутки в раздел под названием Сводка по модели. Запишите значение в столбце R квадрат и ярлык это значение
 R2.
R2.
- Используйте мышь для прокрутки в раздел под названием Сводка по модели. Запишите значение в столбце R квадрат и ярлык это значение
- Повторите шаги 2.1.1 через 2.1.4, используя только
3. вычислительные компоненты уникальный, общие и необъяснимые расхождения
- Откройте программное обеспечение для управления данными.
- Введите метки всего R2,
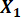 R2, и
R2, и  R2 в ячейки A1, B1 и C1, соответственно.
R2 в ячейки A1, B1 и C1, соответственно. - Введите значение2 всего Rот шага 2.1.5.1 в ячейке A2.
- Введите
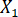 Rзначение2 шага 2.2.2.1 в ячейке B2.
Rзначение2 шага 2.2.2.1 в ячейке B2. - Введите
 Rзначение2 шага 2.3.2.1 в ячейке C2.
Rзначение2 шага 2.3.2.1 в ячейке C2. - Вычислить уникальный дисперсию переменных 1 (U
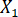 R2) в программное обеспечение для управления данными.
R2) в программное обеспечение для управления данными.- В ячейке D2 типа: «= A2-C2» (то есть, всего R2 минус
 R2). В ячейке D1 ярлык это значение U
R2). В ячейке D1 ярлык это значение U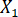 R2.
R2.
- В ячейке D2 типа: «= A2-C2» (то есть, всего R2 минус
- Вычислить уникальный дисперсию переменных 2 (U
 R2) в программное обеспечение для управления данными.
R2) в программное обеспечение для управления данными.- В ячейке E2 типа: «= А2-В2» (то есть, всего R2 минус
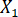 R2). В ячейке E1 ярлык это значение U
R2). В ячейке E1 ярлык это значение U R2.
R2.
- В ячейке E2 типа: «= А2-В2» (то есть, всего R2 минус
- Расчет общей разницы между переменными 1 и 2 (C
 R2) в программное обеспечение для управления данными.
R2) в программное обеспечение для управления данными.- В ячейке F2 типа: «= A2-D2-E2» (то есть, всего R2 минус U
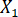 R2 минус U
R2 минус U R2). В ячейке F1 ярлык это значение C
R2). В ячейке F1 ярлык это значение C R2.
R2.
- В ячейке F2 типа: «= A2-D2-E2» (то есть, всего R2 минус U
- Вычислите Необъяснимые расхождения (e) в программное обеспечение для управления данными.
- В ячейке G2 типа: «= 1-А2» (т.е., R1-всего2). В ячейке G1 ярлык это значение е.
4. участок UX1R2, UX2R2,2X1X2RC и e значения
Примечание: Выводятся значения в ячейки D2 и E2, F2, G2.
- Щелкните и перетащите указатель мыши над ячейки D2, E2, F2 и G2, чтобы выделить данные.
- Нажмите кнопку Вставить на ленте программного обеспечения для управления данными.
- Нажмите на графики | Круговая диаграмма | круговая диаграмма 2-Д.
Результаты
Целью данного исследования было изучить вклад уникальных и общей дисперсии языка (L) и декодирование (D) для прогнозирования, чтение (R) в классах 1, 7 и 10 в штате Флорида, состояние которого население являются представитель нации целом. Там были две гипотезы относительно прогнозов дисперсии, объяснил прочитанного. Во-первых после начальных классов, уникальный вклад D значительно уменьшится, и уникальный вклад L будет увеличиваться. Во-вторых уникальный вклад L и общий вклад D и L будет значительно составляют большинство расхождений за пределами начальных классов.
Участники были 372 студентов в классе 1 299 студентов в классе 7 и 122 студентов в классе 10 в общеобразовательных классах из 18 школ в двух крупных городских округов в штате Флорида (один в Северной Флориде и другой-в Центральной Флориде). Изучение руководящими принципами для человека предметов и было получено согласие родителей. Этничность разбивка различных классов для исследования было: примерно 30% черный; 30% испаноязычных; 30% белый; 5% азиатов, 3% культур; 2% другие. Спектр участия в программе федерального обед на 18 участвующих школ был от 21,5% до 100%, при этом средний показатель 59%.
Сингл, наблюдаемый меры D, L и R были отобраны для регрессионного анализа. Мера декодирования была ограничена (45 s) прицел слово декодирования из теста слово чтения эффективности-2-22. L измерялась восприимчивы лексики тест, Peabody картина лексики тест (PPVT-4)23, широко используется в участвующих школ. В этой мере студенты-четыре фотографии и указывают на то, что изображает слово эксперт говорит. R оценивалась с национально нормированных прочитанного тестирования, ворота-Макгинити чтение тест-4 (GMAT-4)24. GMAT-4 осуществляется в небольших группах по 10 студентов в классе 1. Студентов читать части прохода и указать изображение, которое соответствует к проходу. GMAT-4, управляемые группы в 7 и 10 классах. Проходы состоят из литературных и информационного текста и вопросы литерала и логически выведенная и появляются в форме множественного выбора. Студенты могут оглянуться на проход. Для всех трех мер коэффициенты надежности были выше 0.90. Сократить время тестирования использовался планируемых недостающих данных дизайн с тремя формами. D и L мер велись на один сессии и прочитанного тест в рамках другого сеанса.
Регрессионный анализ для 1 класса приходилось 60% общей дисперсии прочитанного. Отдельные расхождения модели показали, что доля дисперсии прочитанного благодаря D 43% и что отдельно, доля дисперсии прочитанного за L составила 36%. Эти оценки дисперсии являются квадрат корреляции из отдельных статистических моделей каждый предсказатель и результат, и поэтому их сумма от отдельных моделей (43 + 36 = 79) было больше, чем общее количество объяснил дисперсию (60%). Когда общая разница в классе 1 было разложено на уникальные и общие эффекты, D уникально объяснил, что 24% дисперсии в R и L однозначно объяснить 17% (см. Рисунок 1). Общая дисперсия D и L был 19%.
Рисунок 1. Всего % дисперсии, объяснил в класс 1 прочитанного, разложить на уникальные и общие эффекты языка и декодирования и необъяснимые расхождения. Пожалуйста, нажмите здесь, чтобы посмотреть большую версию этой фигуры.
В 7 класс регрессионный анализ приходилось 53% общей дисперсии прочитанного. Отдельные расхождения модели показали, что доля дисперсии прочитанного благодаря D 25% и доля дисперсии прочитанного за L составила 46%. Рисунок 2 показывает, что D однозначно объяснить 7% дисперсии в R и L объяснил 28%. Общая дисперсия D и L в объяснении что вариативность в R 18%.
Рисунок 2. Всего % дисперсии, объяснил в 7 класс прочитанного, разложить на уникальные и общие эффекты языка и декодирования и необъяснимые расхождения. Пожалуйста, нажмите здесь, чтобы посмотреть большую версию этой фигуры.
В 10 классе регрессионный анализ приходится 61% общей дисперсии прочитанного. Отдельные расхождения модели показали, что доля дисперсии прочитанного благодаря D 19% и доля дисперсии прочитанного за L составила 54%. Рисунок 3 показывает, что D однозначно приходится 6% дисперсии, тогда как L однозначно приходится 42% дисперсии. Общая дисперсия D и L в объяснении что вариативность в R 13%.

Рисунок 3. Всего % дисперсии, объяснил в 10 классе прочитанного, разложить на уникальные и общие эффекты языка и декодирования и необъяснимые расхождения. Пожалуйста, нажмите здесь, чтобы посмотреть большую версию этой фигуры.
Обсуждение
Существует три важнейшие шаги в протоколе для разложения вариативность в R в уникальный и общие отклонения вследствие L и D. Во-первых вычесть R2 L-только модели от полной модели для получения уникальный R2 D. Во-вторых вычтите R2 для D-только модели от полной модели для получения уникальный R2 для третьего л, для получения общей дисперсии, объясняется L и D, вычесть сумму двух уникальных R2 от R2 для полной модели.
Изменения в протокол будет необходимо, если латентных переменных для D и L заменил Макетные коды для наблюдаемых меры приурочен декодирования и восприимчивым словарь, используемый здесь и если контроля переменных, таких как социально экономическое положение (СЭС), пол и гонки / этнической принадлежности добавляются к модели. Альтернативы для печати результатов в круговые диаграммы может также рассматриваться, например, с помощью диаграмм Венна. Круговые диаграммы были использованы здесь, так что процент Необъяснимые расхождения, а также уникальный и общей разницы может быть отображена.
Существуют ограничения на применение метода, как показано в этом исследовании. Чтобы упростить протокол, мы выбрали один наблюдаемый мера D, L и R вместо скрытой переменной моделирования подход, который мы обычно принимают для управления измерения ошибка19. Мы устранены контроля переменных, таких как SES, пола и расы/этнической принадлежности и использовать кросс-секционные данные с планируемых недостающих данных дизайн вместо полных продольных данных. Мы сосредоточены на разлагающихся разница на уровне каждого студента, а не кластеризации студентов в классах и школах. Наконец метод, показанный в протоколе для разложения дисперсии в процентах уникальных и общего воздействия L и D в прогнозирования R дает описательные результаты. Существует нет простого способа получить официальный статистический тест значение общей дисперсии.
Эта техника для разложения вариативность в R в уникальный и общие эффекты благодаря L и D имеет значительные преимущества перед существующими методами глядя исключительно на уникальные эффекты. Самое главное техника иллюстрирует, как индивидуальные характеристики различие covary и как один уникальный эффект может бледно по сравнению с эффект совместно с другой характеристикой. Анализы, вытекающие из текущего протокола, показали, что значительные суммы дисперсии прочитанного вследствие общего воздействия D и L (начиная с 19% в классе 1 до 13% в 10 классе) появились приехать за счет уникальной вклад в D над оценками. Иными словами результаты регрессии показали, что снижение доли дисперсии приходится на D с 43% в классе 1 до 25% в классе 7-19% в 10 классе. Однако когда разница была разлагается, уникальный вклад в классе 1 D было лишь 24% и что снизился в учащихся 7 классов и 10-7% и 6%, соответственно. Этот вывод имеет важные последствия образования, потому что акцент на декодирование в выступлениях в начальных классах приходит от уникального эффекта D в результаты регрессии несмотря на слабое воздействие декодирования вмешательств в верхней начальных и гимназический цикл в мета анализ25. Количество общей дисперсии, что D и L вместе объяснить в прогнозировании прочитанного, особенно в начальных классах, свидетельствует о том, что более учебных должны быть акцент на интеграции языковых знаний в ,слова уровень2627.
Результаты регрессии для L показал довольно постоянным картину л вносит значительную долю дисперсии для прочитанного через классы, 36% в классе 1 до 54% в 10 классе. Однако когда использовался метод разложения дисперсии, уникальный вклад L над оценками показал резкое увеличение по сравнению с 17% в классе 1 до 28% в классе 7, до 42% в 10 классе. Вывод L приходится так много разница в средних классах в R является еще более очевидной в SVR исследования, проведенные с латентной переменной моделирования подход16,17,19 и предлагает значение инструкции на языковые элементы, которые делают текст сплоченной26,28.
Раскрытие информации
Авторы заявляют, что они не имеют никаких финансовых интересов.
Благодарности
Исследования, сообщили здесь было поддержано, Институт педагогических наук, Департамент образования США, через subaward в государственный университет Флориды от Грант R305F100005 в Educational Testing Service в рамках чтения для понимания Инициативы. Высказанные мнения принадлежат авторам и не представляют взгляды института, Департамент образования США, Educational Testing Service или университет штата Флорида.
Материалы
| Name | Company | Catalog Number | Comments |
| IBM SPSS Statistics Software | IBM | ||
| Microsoft Office Excel | Microsoft |
Ссылки
- Gough, P., Tunmer, W. Decoding, reading, and reading disability. Remedial and Special Education. 7, 6-10 (1986).
- Quinn, J. M., Wagner, R. K. Using meta-analytic structural equation modeling to study developmental change in relations between language and literacy. Child Development. , in press (2018).
- Chen, R. S., Vellutino, F. Prediction of reading ability: A cross-validation study of the simple view of reading. Journal of Literacy Research. 29 (1), 1-24 (1997).
- Catts, H., Hogan, T., Adlof, S. Developmental changes in reading and reading disabilities. Connections between language and reading disabilities. Catts, H., Kamhi, A. , Erlbaum. Mahwah, NJ. (2005).
- Gough, P., Hoover, W., Peterson, C. Some observations on the simple view of reading. Reading comprehension difficulties. Cornoldi, C., Oakhill, J. , Erlbaum. Hillsdale, NH. (1996).
- Dreyer, L., Katz, L. An examination of "The Simple View of Reading.". Haskins Laboratories Status Report on Speech Research. SR-111/112. , 161-166 (1992).
- Neuhaus, G., Roldan, L., Boulware-Gooden, R., Swank, P. Parsimonious reading models: Identifying teachable subskills. Reading Psychology. 27, 37-58 (2006).
- Kershaw, S., Schatschneider, C. A latent variable approach to the simple view of reading. Reading and Writing. 25, 433-464 (2012).
- Hoover, W., Gough, P. The simple view of reading. Reading and Writing. 2, 127-160 (1990).
- Adlof, S., Catts, H., Little, T. Should the simple view of reading include a fluency component? Reading & Writing. 19, 933-958 (2006).
- Anthony, J., Davis, C., Williams, J., Anthony, T. Preschoolers' oral language abilities: A multilevel examination of dimensionality. Learning and Individual Differences. 35, 56-61 (2014).
- Bornstein, M., Hahn, C., Putnick, D., Suwalsky, J. Stability of core language skill from early childhood to adolescence: A latent variable approach. Child Development. 85, 1346-1356 (2014).
- Protopapas, A., Simos, P., Sideridis, G., Mouzaki, A. The components of the simple view of reading: A confirmatory factor analysis. Reading Psychology. 33, 217-240 (2012).
- Tomblin, J. B., Zhang, X. The dimensionality of language ability in school-age children. Journal of Speech, Language, and Hearing Research. 49, 1193-1208 (2006).
- Foorman, B., Herrera, S., Petscher, Y., Mitchell, A., Truckenmiller, A. The Structure of Oral Language and Reading and Their Relation to Comprehension in grades kindergarten through grade 2. Reading and Writing. 28 (5), 655-681 (2015).
- Foorman, B., Koon, S., Petscher, Y., Mitchell, A., Truckenmiller, A. Examining General and Specific Factors in the Dimensionality of Oral Language and Reading in 4th-10th Grades. Journal of Educational Psychology. 107 (3), 884-899 (2015).
- Kieffer, M., Petscher, Y., Proctor, C. P., Silverman, R. Is the whole greater than the sum of its parts? Modeling the contributions of language comprehension skills to reading comprehension in the upper elementary grades. Scientific Studies of Reading. 20 (6), 436-454 (2016).
- Kim, Y. S. G., Park, C., Park, Y. Dimensions of discourse level oral language skills and their relation to reading comprehension and written composition: an exploratory study. Reading and Writing. 28, 633-654 (2015).
- Foorman, B., Petscher, Y., Herrera, S. Unique and common effects of decoding and language factors in predicting reading comprehension in grades 1-10. Learning and Individual Differences. 63, 12-23 (2018).
- Perfetti, C. Reading ability: Lexical quality to comprehension. Scientific Studies of Reading. 11 (4), 357-383 (2007).
- Perfetti, C., Stafura, J. Word knowledge in a theory of reading comprehension. Scientific Studies of Reading. 18 (4), 22-37 (2014).
- Torgesen, J., Wagner, R., Rashotte, C. Test of Word Reading Efficiency. , 2nd ed, ProEd. Austin, TX. (2012).
- Dunn, L., Dunn, D. Peabody Picture Vocabulary Test-4. , Pearson. San Antonio, TX. (2007).
- MacGinitie, W., MacGinitie, R., Maria, K., Dreyer, L. Gates-MacGinitie Reading Tests. , 4th ed, Riverside Publishing. Rolling Meadows, IL. (2000).
- Wanzek, J., Wexler, J., Vaughn, S., Ciullo, S. Reading interventions for struggling readers in the upper elementary grades: a synthesis of 20 years of research. Reading & Writing. 23, 889-912 (2010).
- Foorman, B., Petscher, Y., Stanley, C., Herrera, S. Latent profiles of reading and language and their association with standardized reading outcomes in kindergarten through tenth grade. Journal of Research on Educational Effectiveness. 10 (3), 619-645 (2017).
- Lesaux, N. K., Kieffer, M. J., Kelley, J. G., Harris, J. Effects of academic vocabulary instruction for linguistically diverse adolescents: Evidence from a randomized field trial. American Educational Research Journal. 51 (6), 1159-1194 (2014).
- Lawrence, J., Crosson, A., Paré-Blagoev, E., Snow, C. Word generation randomized trial: Discussion mediates the impact of program treatment on academic word learning. American Educational Research Journal. 52 (4), 750-786 (2015).
Перепечатки и разрешения
Запросить разрешение на использование текста или рисунков этого JoVE статьи
Запросить разрешениеСмотреть дополнительные статьи
This article has been published
Video Coming Soon
Авторские права © 2025 MyJoVE Corporation. Все права защищены