Caracterização de Componentes Magnéticos

Fonte: Ali Bazzi, Departamento de Engenharia Elétrica da Universidade de Connecticut, Storrs, CT.

O objetivo deste experimento é alcançar a experiência prática com diferentes componentes magnéticos a partir do design e perspectivas materiais. Este experimento abrange curvas B-H de material magnético e design indutor através da identificação de fatores de design desconhecidos. A curva B-H de um elemento magnético, como um indutor ou transformador, é uma característica do material magnético formando o núcleo em torno do qual os enrolamentos são embrulhados. Esta característica fornece informações sobre a densidade de fluxo magnético que o núcleo pode lidar com relação à corrente que flui nos enrolamentos. Ele também fornece informações sobre limites antes que o núcleo esteja magneticamente saturado, ou seja, quando empurrar mais corrente através da bobina não leva a mais fluxo magnético.

A curva B-H pode ser identificada usando um circuito simples. Utilizando a lei de Ampere, a intensidade do fluxo magnético (H) é proporcional à corrente em uma bobina; por exemplo, para uma única bobina n-turncarregando uma corrente (i) enrolada em torno de um núcleo de comprimento médio(l) e área transversal(A),a lei de Ampere rende,

(1)

Além disso, a tensão através da bobina (v) pode ser determinada pela taxa de fluxo de mudança dφ/dt usando a lei de Faraday. Para a mesma bobina descrita anteriormente,

(2)

A densidade de fluxo (B) também é definida como,

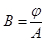(3)

que, portanto, pode ser escrito como,

(4)

Portanto, para estimar a curva B-H de um material, i e o tempo integral de v pode ser usado. O dimensionamento de volta para as quantidades reais de B e H é possível quando N, l, e A são conhecidos.

Para medir o tempo integral de v,pode-se utilizar um simples circuito R-C em paralelo com a bobina (Fig. 1). O divisor R-C deve ter R >> X_C na frequência de operação para que v_R≈v. Usando esta suposição, medir a tensão do capacitor v_C dá uma aproximação razoável do tempo integral de v desde então,

(5)

O sinal negativo é eficaz para a representação do domínio do tempo, mas deve ser descartado ao lidar com RMS e quantidades máximas, portanto é comum usar,

(6)

Figura 1: Circuito de teste para determinar a curva B-H de um indutor. Clique aqui para ver uma versão maior desta figura.

1. Identificação relativa de permeabilidade

Siga o procedimento para encontrar a permeabilidade relativa do pequeno indutor (núcleo ferrite amarelo/branco). As dimensões principais são mostradas em Fig. 2, e o número de curvas é N=75.

1. Utilizando um medidor LCR, meça a indutância do indutor a 120 Hz e 1000 Hz.
2. Construa o circuito em Fig. 1 em uma placa proto, mas mantenha a saída do gerador de função desconectada da placa proto.
3. Verifique uma sonda de tensão diferencial e uma sonda corrente para não obter deslocamentos com a sonda atual conectada no canal 1 e a sonda de tensão conectada no canal 2.
4. Observe os fatores de escala para a sonda diferencial na própria sonda e no escopo. Defina a sonda diferencial para 1/20 para uma melhor resolução.
5. Defina a sonda atual para 100 mV/A na própria sonda e 1X no escopo. Lembre-se que esses fatores de escala precisam ser usados na realização de cálculos.
6. Defina a saída do gerador de função (50 Ω conector de saída BNC) no pico de 10 V e na forma de onda sinusoidal de 1000 Hz. Observe a forma de onda usando a sonda de tensão diferencial.
7. Deixe o gerador de função ligado mesmo quando desconectado, mas evite encurtar seus terminais. Desligar o gerador de função redefine muitas configurações.
8. Conecte as sondas de corrente e tensão para medir v_C e i.
9. Verifique se o circuito está como desejado e se todas as conexões são mantidas.
10. Conecte o gerador de função ao circuito.
11. Faça uma captura de tela da corrente e tensão medidos com pelo menos três períodos mostrados, além dos valores de pico ou RMS dos sinais medidos.
12. A partir do menu "Exibir" no escopo, altere o formato de exibição de "YT" para "XY".
13. Observe a curva B-H ajustando os botões de ajuste vertical do canal 1 e do canal 2 até que a curva se encaixe na tela do escopo.
14. Para ver uma curva mais estável, use a opção "persistir" no menu de exibição em uma configuração de 1 ou 2 s.
15. Faça uma captura de tela da curva B-H medida.
16. Ajuste a frequência do gerador de função para 120 Hz e retome a captura de tela da curva B-H depois de ajustar as configurações da curva conforme necessário.
17. Desconecte o gerador de função e remova o indutor. Mantenha o resto do circuito intacto.

Figura 2: Dimensões do núcleo indutor menor. Clique aqui para ver uma versão maior desta figura.

2. Identificando o número de curvas

O maior indutor preto (Bourns 1140-472K-RC) tem um número desconhecido de curvas. Para simplificar os cálculos, assuma que o núcleo seja um solenoide de núcleo de ar com um raio de 1,5 cm e comprimento de 2,5 cm. Se essa suposição não for tomada, a geometria do núcleo terá que ser considerada e complicará os cálculos. No entanto, essa suposição ainda é razoável, dado que com um solenoide, o fluxo tem que passar pelo ar em ambos os lados do dispositivo e o ar é o meio de caminho dominante.

1. Utilizando o medidor LCR, meça a indutância do indutor fornecido em 120 Hz e 1000 Hz.
2. Coloque o indutor no circuito mostrado na Fig. 1, que ainda deve estar intacto da parte anterior do experimento.
3. Verifique uma sonda de tensão diferencial e uma sonda corrente para não obter deslocamentos com a sonda atual conectada no canal 1 e a sonda de tensão conectada no canal 2.
4. Observe os fatores de escala para a sonda diferencial na própria sonda e no escopo. Defina a sonda diferencial para 1/20 para uma melhor resolução.
5. Defina a sonda atual para 100 mV/A na própria sonda e 1X no escopo. Lembre-se que esses fatores de escala precisam ser usados ao fazer cálculos utilizando quaisquer medições ou capturas de dados para análise suplementar.
6. Defina a saída do gerador de função (50 Ω conector de saída BNC) no pico de 10 V e na forma de onda sinusoidal de 1000 Hz. Observe a forma de onda usando a sonda de tensão diferencial.
7. Deixe o gerador de função ligado mesmo quando desconectado, mas evite encurtar seus terminais. Desligar o gerador de função redefine muitas configurações.
8. Conecte as sondas de corrente e tensão para medir v_C e i.
9. Verifique o circuito e certifique-se de que as conexões estão conforme desejado.
10. Conecte o gerador de função ao circuito.
11. Faça uma captura de tela da corrente e tensão medidos com pelo menos três períodos mostrados, além dos valores de pico ou RMS dos sinais medidos.
12. A partir do menu "display" no escopo, altere o formato de exibição de "YT" para "XY".
13. Observe a curva B-H ajustando os botões de ajuste vertical do canal 1 e do canal 2 até que a curva se encaixe na tela do escopo.
14. Para ver uma curva mais estável, use a opção "persistir" no menu de exibição em uma configuração de 1 ou 2 s.
15. Faça uma captura de tela da curva B-H medida.
16. Ajuste a frequência do gerador de função para 120 Hz e retome a captura de tela da curva B-H depois de ajustar as configurações da curva conforme necessário.
17. Desligue o gerador de funções e desmonte o circuito.

Curva 3.B-H de um transformador de 60 Hz

O transformador usado nesta demonstração desce de 115 V RMS para 24 V RMS, mas só pode ser usado para caracterização de curva B-H neste experimento, assim, apenas os terminais 120 V RMS são usados. As dimensões do transformador são mostradas na Fig. 3.

1. Utilizando o medidor LCR, meça a indutância do enrolamento do lado V de 115 a 120 Hz (mais próximo dos 60 Hz classificados).
2. Certifique-se de que o interruptor de desconexão trifásica está na posição desligada.
3. Conecte o cabo trifásico ao VARIAC.
4. Construa o circuito mostrado em Fig. 4. Que o transformador fique ao lado do proto-board. Use cabos de banana para conectar AC1 e N do VARIAC à placa proto.
5. Certifique-se de que o VARIAC está definido em 0%.
6. Verifique uma sonda de tensão diferencial e uma sonda corrente para não obter deslocamentos com a sonda atual conectada no canal 1 e a sonda de tensão conectada no canal 2.
7. Observe os fatores de escala para a sonda diferencial na própria sonda e no escopo. Defina o dimensionamento diferencial da sonda para 1/200.
8. Defina a sonda atual para 100 mV/A na própria sonda e 1X no escopo. Lembre-se que esses fatores de escala precisam ser usados ao fazer cálculos.
9. Conecte as sondas de corrente e tensão para medir v_C e i.
10. Verifique o circuito.
11. Ligue o interruptor de desconexão trifásico e ajuste lentamente o VARIAC até que 90% seja atingido.
12. Faça uma captura de tela da corrente e tensão medidos com pelo menos três períodos mostrados, além dos valores de pico ou RMS dos sinais medidos.
13. A partir do menu "Exibir" no escopo, altere o formato de exibição de "YT" para "XY".
14. Observe a curva B-H ajustando os botões de ajuste vertical do canal 1 e do canal 2 até que a curva se encaixe na tela do escopo.
15. Para ver uma curva mais estável, use a opção "persistir" no menu de exibição em uma configuração de 1 ou 2 s.
16. Faça uma captura de tela da curva B-H medida.
17. Restaure o VARIAC para 0%, desligue o interruptor de desconexão e desmonte o circuito.

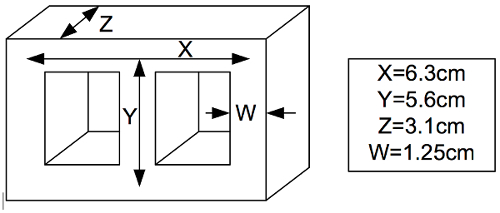
Figura 3: Dimensões do núcleo do transformador. Clique aqui para ver uma versão maior desta figura.

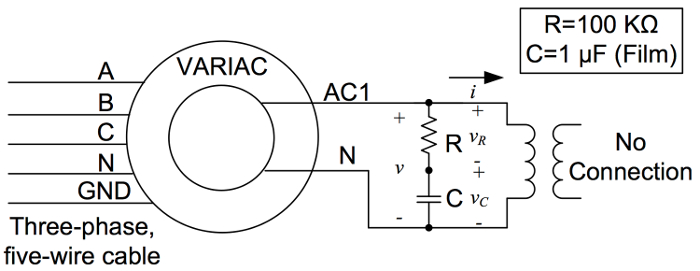
Figura 4: Circuito de teste para determinar a curva B-H de um transformador de 60 Hz. Clique aqui para ver uma versão maior desta figura.

Para encontrar a permeabilidade relativa do material central, duas abordagens podem ser utilizadas. A primeira abordagem é usar um medidor LCR, onde a indução (L) de uma bobina feita com um número conhecido de curvas (N) é medida, e então a permeabilidade relativa pode ser calculada da seguinte forma:

Relutância do núcleo: (7)

A permeabilidade relativa (μ_r) é assim:

(8)

onde μ_o é a permeabilidade do vácuo, l é o comprimento médio do núcleo em m, e A é a área transversal do núcleo em m².

Por exemplo, se um núcleo toroidal for usado com um raio interno r₁=1 cm, um raio externo r₂=2 cm, uma área transversal de 1 cm², e o medidor LCR lê 1 μH para 10 voltas, então:

l=2π(r₂-r₁) =2π cm, e μ _r=50.000.

O segundo método utiliza a curva B-H medida. Na região linear, visível ou aproximada, a permeabilidade relativa pode ser encontrada a partir da inclinação (B=μ_rμ_oH) para cada frequência. Para encontrar valores B e H, o dimensionamento apropriado deve ser realizado para fatores de sonda, elementos de circuito e dimensões do núcleo usando medições anteriores.

Em uma abordagem semelhante a encontrar a permeabilidade relativa, o número de curvas pode ser encontrado se a permeabilidade relativa for desconhecida. Isso pode ser alcançado manipulando as equações anteriores para encontrar N.

Para ferrites, μ_r está na ordem de vários milhares, enquanto para ligas de aço e aço, μ _r está na ordem de dezenas ou centenas.

Embora os indutores e outros dispositivos eletromagnéticos (por exemplo,transformadores) sejam muito comuns em muitos sistemas elétricos, eletrônicos e mecânicos, comprar indutores para uma aplicação específica não é trivial. Mesmo quando um indutor é comprado, as informações do datasheet ainda podem ter ambiguidades no material real, número de curvas e outros detalhes. Os testes neste experimento são especialmente úteis para engenheiros e técnicos que planejam construir seus próprios indutores ou caracterizar os que estão fora da prateleira. Isso é comum com aplicações eletrônicas de energia (por exemplo,conversores DC/DC) bem como aplicações de acionamento de motor elétrico(por exemplo,indutores de filtro CA) onde mais informações são desejadas sobre o indutor em mãos.