Stanza di Ames

Fonte: Laboratorio di Jonathan Flombaum—Johns Hopkins University

La sfida più difficile della percezione visiva è spesso descritta come quella di recuperare informazioni sullo spazio tridimensionale da retine bidimensionali. La retina è il tessuto sensibile alla luce all'interno dell'occhio umano. La luce viene riflessa dagli oggetti nel mondo, proiettando proiezioni sulla retina che stimolano queste cellule sensibili alla luce. Gli oggetti che sono fianco a fianco nel mondo produrranno stimolazioni fianco a fianco sulla retina. Ma gli oggetti che sono più distanti dall'osservatore non possono produrre stimoli più distanti, rispetto agli oggetti vicini che sono. La distanza, la terza dimensione, è collassata sulla retina.

Quindi, come vediamo in tre dimensioni? La risposta è che il cervello umano applica una varietà di ipotesi ed euristiche al fine di fare inferenze sulle distanze dati gli input ricevuti sulla retina. Nello studio della percezione, c'è una lunga tradizione di usare le illusioni visive come un modo per identificare alcune di queste euristiche e ipotesi. Se i ricercatori sanno quali trucchi sta usando il cervello, dovrebbero essere in grado di ingannare il cervello a vedere le cose in modo impreciso. Questo video ti mostrerà come costruire una Ames Room, un'illusione visiva che illustra uno dei presupposti applicati dal sistema visivo umano per recuperare la profondità visiva.

1. Materiali

1. Per costruire una Ames Room avrai bisogno di quattro pezzi di cartone, ciascuno alto 1 piede. I quattro pezzi dovrebbero variare in lunghezza, tra cui un pezzo da 2 piedi, due pezzi da 1 ft e un pezzo lungo 1,5 piedi.
2. Avrai anche bisogno di due figurine di qualche tipo, action figure, soldatini, persino animali di peluche faranno il trucco. I due dovrebbero essere all'incirca della stessa altezza e più corti di 3/4 di piedi di altezza.
3. Sarà inoltre necessario un taglierino e colla o nastro.

2. Assemblaggio della stanza di Ames

1. Inizia con uno dei due pezzi di cartone da 1 ft. Metti un centesimo su di esso, proprio al centro, e usa il taglierino per tagliare intorno al penny per produrre un buco. Questa sarà l'apertura per la Ames Room.
2. La Figura 1 illustra schematicamente le tre fasi iniziali dell'assemblaggio, descritte al punto 2.2.-2.4. Alza il pezzo con il foro e alla sua destra attacca l'altro pezzo di cartone da 1 piede, in modo che i due formino un angolo retto. Avrai un oggetto che assomiglia a quello nella Figura 1a, se guardato dall'alto.

Figura 1: Costruire una stanza di Ames equivale a costruire (da cartone) un poligono irregolare a quattro lati. Il primo passo è scolpire uno spioncino delle dimensioni di un centesimo in un pezzo di cartone da 1 piede. Quindi attacca un pezzo di cartone di dimensioni uguali per produrre un angolo retto in piedi come quello mostrato in (A). Quindi, attaccare un pezzo di cartone da 2 piedi, anche ad angolo retto, a sinistra del pezzo con lo spioncino. Il risultato è schematizzato in B. Infine, attacca un pezzo di cartone da 1,5 piedi per chiudere il poligono. Il prodotto finale è riportato in C.

3. Ora attacca il pezzo da due piedi sull'altro lato del pezzo con l'apertura. Avrai un oggetto che assomiglia a quello nella Figura 1b se guardato dall'alto.
4. Infine, attacca il pezzo da 1,5 piedi per chiudere la struttura. Avrai un poligono a quattro lati come quello nella Figura 1c.
5. Per completare la stanza di Ames e produrre l'illusione prendi le due figurine e posizionane una a ciascuno dei vertici dove il cartone da 1,5 piedi si attacca al resto della struttura. Nella Figura 2, queste due posizioni sono indicate da cerchi verdi. Le figurine dovrebbero essere rivolte verso l'apertura.

Figura 2: I punti verdi indicano il posizionamento relativo delle figurine all'interno della Sala Ames. Per produrre l'illusione più forte, è fondamentale che le due figurine siano posizionate ai due vertici ad angolo non retto del poligono.

3. Vedere l'illusione

1. Per vedere l'illusione, basta guardare nella stanza di Ames guardando attraverso l'apertura.

Cosa vedi quando guardi nella stanza di Ames? La Figura 3 schematizza l'effetto: la statuetta a destra dovrebbe apparire molto più grande di quella a sinistra, anche se sai che hanno le stesse dimensioni.

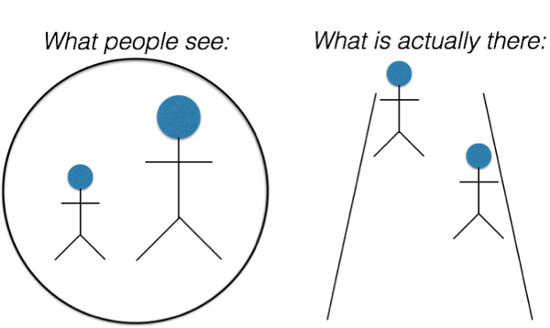
Figura 3: Rappresentazione schematica di ciò che le persone vedono nella Sala di Ames, rispetto al fatto della questione, cioè,ciò che è effettivamente lì. Il lato destro della figura mostra le vere dimensioni relative e le distanze delle figurine nella stanza: sono ugualmente alte e quella a sinistra è più lontana dallo spettatore. Ma quando si guarda attraverso l'apertura, l'illusione, raffigurata a sinistra, è che la figurina a sinistra sembra essere in piedi accanto alla persona a destra, e quella figurina sembra anche molto più piccola.

Cosa sta succedendo? Prima di spiegare la Sala Ames in particolare, dobbiamo considerare il problema generale di percepire dimensioni e profondità allo stesso tempo. La proiezione che un oggetto produce sulla retina varierà di dimensioni in proporzione alle dimensioni dell'oggetto; ma le proiezioni varieranno anche di dimensioni in funzione della distanza di un oggetto dalla superficie su cui proietta (in questo caso la retina). In altre parole, una proiezione molto grande sulla retina potrebbe significare che l'oggetto rilevante è molto grande e ragionevolmente lontano dall'osservatore, oppure potrebbe significare che l'oggetto rilevante è piccolo, ma molto vicino. Gli oggetti grandi possono lanciare piccole proiezioni quando sono lontani e i piccoli oggetti possono lanciare grandi proiezioni quando sono vicini. Separare dimensioni e distanza è una delle principali sfide per la visione 3D. La Figura 4 schematizza questo problema generale in riferimento a due alberi della stessa dimensione ma a distanze relative diverse da un osservatore.

Figura 4: Un diagramma schematico per illustrare il problema della percezione simultanea di dimensioni e distanza. Sul lato sinistro della figura ci sono due alberi di uguale altezza. Alla loro destra, c'è un osservatore, indicato come un occhio. A causa della posizione relativa dell'osservatore rispetto agli alberi e della fisica della proiezione ottica, l'albero a sinistra dell'osservatore proietta una riflessione molto più piccola sulla retina dell'osservatore, rispetto all'albero a destra. Questo perché l'albero a destra è più vicino all'osservatore. Ma date le proiezioni sulla retina bidimensionale, cosa dovrebbe pensare l'osservatore, l'albero a sinistra è più piccolo, o solo più lontano?

Tornando ora alla Stanza di Ames, ciò che le illusioni specifiche dimostrano è uno dei trucchi che il cervello usa per stimare le dimensioni degli oggetti e le distanze degli oggetti. In particolare, il cervello applica un presupposto: presuppone che, in assenza di forti prove compensanti, che le strutture si connettano tra loro ad angolo retto.

Diamo ora un'occhiata alla configurazione di Ames Room per capire come l'illusione sfrutta tale assunto. Le pareti della stanza sono tutte dello stesso colore, e guardando attraverso una piccola apertura le persone non possono dire che la parete lontana è diagonale. Quindi il cervello presume che sia dritto, che la stanza di Ames sia rettangolare anziché irregolare. L'implicazione di tale ipotesi è che la statuetta sul lato sinistro della stanza (rispetto alla vista dell'apertura) è molto più vicina all'osservatore di quanto non sia in realtà. In effetti, l'implicazione è che si trova alla stessa distanza della statuetta a destra. Poiché in realtà è più lontana, la statuetta a sinistra proietta un'immagine più piccola sulla retina dell'osservatore rispetto alla statuetta a destra. Ma il cervello ha fatto un'ipotesi che implica che sono la stessa distanza. Quindi, cosa potrebbe spiegare le differenze nelle dimensioni delle proiezioni di figurine? Il cervello viene ingannato: ragiona che la statuetta a sinistra deve in realtà essere molto più piccola di quella a destra che produce l'illusione. La Figura 5 illustra questo ragionamento in relazione alla geometria della Sala di Ames.

Figura 5. La stanza di Ames inganna il cervello umano, producendo l'illusione delle dimensioni, sfruttando un'ipotesi che il cervello fa sulla geometria. In particolare, il cervello umano presuppone che le pareti si attacchino l'una all'altra ad angolo retto. Guardando attraverso l'apertura della Stanza di Ames, il cervello non può raccogliere prove compensanti, e quindi applica questa ipotesi. Il risultato è che pensa che la stanza di Ames sia rettangolare, con la parete lontana che occupa le posizioni della linea tratteggiata nella figura. L'implicazione, quindi, è che le due figurine sono affiancate e che la statuetta di sinistra è molto più vicina all'osservatore di quanto non sia accurata. Il cervello si chiede quindi perché due oggetti affiancati proiettino proiezioni di dimensioni così diverse sulla retina. La risposta che dà: devono essere di dimensioni diverse.

Capire come gli esseri umani percepiscono il mondo visivo in 3D è stata una delle principali aree di interesse della ricerca e un importante risultato del moderno studio della percezione. Alcune delle importanti applicazioni che sono sorte, di conseguenza, sono nello sviluppo della tecnologia di visualizzazione 3D e della realtà virtuale. La stanza di Ames nello specifico è stata utilizzata per molto tempo nei film, come una sorta di effetto speciale. Supponiamo che un film debba rappresentare un gigante o qualcuno molto piccolo. Girare scene interne all'interno di una Ames Room può produrre l'illusione per lo spettatore che alcune persone siano molto più grandi (o più piccole) di quanto non siano in realtà. La fotocamera, dopo tutto, è un'apertura.