Method Article
Misurazione sperimentale della velocità di sedimentazione delle particelle sferiche in fluidi viscoelastici a base di tensioattivi non raffinati e confinati
In questo articolo
Riepilogo
Questo documento dimostra la procedura sperimentale per misurare le velocità di sedimentazione terminale delle particelle sferiche nei fluidi viscoelastici diradanti a base di tensioattivi. I fluidi su un'ampia gamma di proprietà reologiche vengono preparati e le velocità di sedimentazione sono misurate per una gamma di dimensioni delle particelle in fluidi e fluidi illimitati tra pareti parallele.
Abstract
Viene effettuato uno studio sperimentale per misurare le velocità terminali di sedimentazione delle particelle sferiche nei fluidi viscoelastici di diradamento a taglio a base di tensioattivi (VES). Le misurazioni sono effettuate per particelle che si depositano in fluidi e fluidi illimitati tra pareti parallele. I fluidi VES su un'ampia gamma di proprietà reologiche sono preparati e caratterizzati reologicamente. La caratterizzazione reologica comporta una costante viscosità di taglio e misurazioni oscillatorie dinamiche-taglio per quantificare rispettivamente le proprietà viscose ed elastiche. Le velocità di sedimentazione in condizioni illimitate sono misurate in becher con diametri di almeno 25 volte il diametro delle particelle. Per misurare le velocità di sedimentazione tra pareti parallele, vengono costruite due celle sperimentali con spaziatura delle pareti diverse. Particelle sferiche di varie dimensioni vengono delicatamente cadute nei fluidi e permettete di depositarsi. Il processo viene registrato con una videocamera ad alta risoluzione e la traiettoria della particella viene registrata utilizzando il software di analisi delle immagini. Le velocità di liquidazione terminale vengono calcolate dai dati.
L'impatto dell'elasticità sulla velocità di sedimentazione nei fluidi illimitati è quantificato confrontando la velocità di sedimentazione sperimentale con la velocità di sedimentazione calcolata dalle previsioni di resistenza anelastica di Renaud et al. 1 I risultati mostrano che l'elasticità dei fluidi può aumentare o diminuire la velocità di sedimentazione. La grandezza della riduzione/aumento è una funzione delle proprietà reologiche dei fluidi e delle proprietà delle particelle. Si osserva che le pareti confinanti causano un effetto di ritardo sulla sedimentazione e il ritardo viene misurato in termini di fattori della parete.
Introduzione
Le sospensioni di particelle nei liquidi si incontrano in applicazioni tra cui la produzione farmaceutica, il trattamento delle acque reflue, la reiniezione del propellente spaziale, la lavorazione dei semiconduttori e la produzione di detergenti liquidi. Nell'industria petrolifera, i fluidi di fratturazione viscoelastica vengono utilizzati per trasportare proppanti (tipicamente sabbia) in fratture idrauliche. Alla cessazione del pompaggio i proppanti mantengono aperta la frattura e forniscono una via conduttiva per il flusso di idrocarburi.
La sedimentazione delle particelle è governata dalla reologia e dalla densità del fluido, dalle dimensioni, dalla forma e dalla densità delle particelle e dall'effetto delle pareti confinanti. Per una particella sferica che si deposita in un fluido newtoniano nel regime di flusso strisciante, la velocità di sedimentazione è data dall'equazione di Stokes, derivata da Stokes nel 1851. Espressioni per calcolare la forza di trascinamento a numeri reynolds più alti sono state presentate dai ricercatorisuccessivi 2-6. Le pareti confinanti riducono le velocità di sedimentazione esercitando un effetto di ritardo sulle particelle. Il fattore di parete, Fw, è definito come il rapporto tra la velocità di sedimentazione terminale in presenza di pareti confinanti alla velocità di sedimentazione in condizioni illimitate. Il fattore muro quantifica l'effetto di ritardo delle pareti confinanti. Molti studi teorici e sperimentali per determinare i fattori delle pareti per le sfere che si depositano nei fluidi newtoniani in diversi tubi di sezione trasversale su una vasta gamma di numeri di Reynolds sono disponibili nellaletteratura 7-13. In tutto, c'è un ampio corpus di informazioni disponibili per determinare la resistenza sulle sfere nei fluidi newtoniani.
Il lavoro passato sulla determinazione della velocità di sedimentazione delle particelle nei fluidi non newoniani, in particolare nei fluidi viscoelastici, è meno completo. Varie previsioni numeriche14-18 e studi sperimentali19-24 sono disponibili in letteratura per determinare la forza di trascinamento su una sfera nei fluidi anelastico della legge di potenza. Usando le previsioni teoriche di Tripathi et al. 15 e Tripathi e Chhabra17, Renaud et al. 1 ha sviluppato le seguenti espressioni per calcolare il coefficiente diresistenza aerodinamica (CD)nei fluidi anelatici della legge di potenza.
Per RePL<0.1 (regime di flusso strisciante)

dove X(n) è il fattore di correzione della resistenzaaerodinamica 13. RePL èil numero di Reynolds per una sfera che cade in un liquido di legge di potenza definito come:
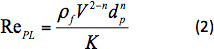
dove ρf è la densità del liquido. Il fattore di correzione della resistenza aerodinamica è stato dotato della seguenteequazione 1:
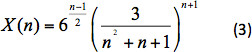
Utilizzando la definizione di coefficiente di trascinamento, la velocità di sedimentazione viene calcolata come:

Per 0.1PL<100
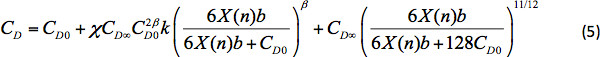
dove X è il rapporto tra l'area della superficie e l'area proiettata della particella ed è uguale a 4 per le sfere. CD0 è il coefficiente di resistenza aerodinamica nella regione di Stokes (RePL < 0,1) dato dall'equazione 1, CD∞ è il valore del coefficiente di resistenza aerodinamica nella regione di Newton (RePL > 5 x 102) ed è uguale a 0,44. I parametri β, b, k sono espressi come:

αo = 3 e α è la correzione per la velocità media di taglio correlata a X(n) come:
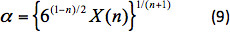
Per calcolare la velocità di sedimentazione viene utilizzato il gruppo adimensionale N d 25:

Nd è indipendente dalla velocità di sedimentazione e può essere calcolato esplicitamente. Utilizzando questo valore e l'espressione del coefficiente di trascinamento nell'equazione 5, RePL può essere risolto in modo iterativo. La velocità di assestamento può quindi essere calcolata utilizzando:
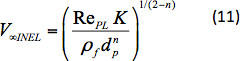
Le espressioni nelle equazioni 1-9 erano basate su previsioni teoriche ottenute per i valori 1 ≥ n ≥ 0,4. Chhabra13 ha confrontato le previsioni delle espressioni di cui sopra con i risultati sperimentali di Shah26-27 (n variava da 0,281-0,762) e Ford et al. 28 (n variava da 0,06 a 0,29). Le espressioni sono state mostrate per prevedere accuratamente i coefficienti di trascinamento. Sulla base di queste analisi, la formulazione di cui sopra può essere utilizzata per calcolare la velocità di sedimentazione delle particelle sferiche nei fluidi della legge di potenza anelastica per 1 ≥ n ≥ 0,06. Questa velocità di sedimentazione prevista nei fluidi anelastico della legge di potenza viene confrontata con la velocità sperimentale nei fluidi viscoelastici della legge di potenza per determinare l'influenza dell'elasticità del fluido sulla velocità di sedimentazione. I passaggi dettagliati sono menzionati nella sezione successiva.
La determinazione della velocità di sedimentazione delle particelle nei fluidi viscoelastici è stata anche un argomento di ricerca con osservazioni variabili da parte di diversi ricercatori; ( i) Nel regime di flusso strisciante gli effetti di assottigliamento del taglio oscurano completamente gli effetti viscoelastici e le velocità di sedimentazione sono in ottimo accordo con le teorie puramente viscose29-32, (ii) le particelle sperimentano una riduzione della resistenza aerodinamica all'interno e all'esterno del regime di flusso strisciante e le velocità di sedimentazione aumentano acausa dell'elasticità 30,33,34, (iii) la velocità di sedimentazione si riduce a causa dell'elasticitàdel fluido 35. Walters e Tanner36 hanno riassunto che per i fluidi Boger (fluidi elastici a viscosità costante) l'elasticità provoca una riduzione della resistenza aerodinamica a bassi numeri di Weissenberg seguita da un miglioramento della resistenza aerodinamica a numeri di Weissenberg più elevati. McKinley37 ha evidenziato che gli effetti esozionali sulla scia della sfera causano l'aumento della resistenza a numeri di Weissenberg più alti. Dopo un esame completo dei precedenti lavori di sedimentazione delle particelle in fluidi viscoelastici illimitati e confinati, Chhabra13 ha evidenziato la sfida di incorporare una descrizione realistica della viscosità dipendente dal tasso di taglio insieme all'elasticità del fluido negli sviluppi teorici. Lo studio degli effetti delle pareti sulla sedimentazione delle particelle sferiche è stato anche un'area di ricerca negli ultimianni 38-42. Tuttavia, tutto il lavoro è stato eseguito sulla sedimentazione di particelle sferiche in tubi cilindrici. Non sono disponibili dati per particelle sferiche che si depositano in fluidi viscoelastiche tra pareti parallele.
Questo lavoro tenta di studiare sperimentalmente la sedimentazione delle sfere nei fluidi viscoelastici diradamento a taglio. L'obiettivo di questo studio sperimentale è comprendere l'impatto dell'elasticità del fluido, del diradamento delle cesoie e del confinamento delle pareti sulla velocità di sedimentazione delle particelle sferiche nei fluidi viscoelastici diradante a taglio. Questo documento si concentra sui metodi sperimentali utilizzati per questo studio insieme ad alcuni risultati rappresentativi. I risultati dettagliati e le analisi sono disponibili in una pubblicazione precedente43.
Protocollo
1. Preparazione dei fluidi
Per questo studio sperimentale viene utilizzato un sistema fluido a base di tensioattivi privo di polimeri, viscoelastico, a due componenti. Questo sistema fluido è stato utilizzato in pozzi di petrolio e gas in molti campi di produzione per trattamenti di fratturazioneidraulica 44,45. Questo sistema fluido viene utilizzato per questo studio perché è otticamente trasparente e la reologia può essere controllata variando sistematicamente le concentrazioni e le proporzioni dei due componenti. Il sistema fluido è costituito da un tensioattiva anionico (come lo xilene solfonato di sodio) come componente A e da un tensioattiva cationico (come N,N,N-trimetil-1-ottadecamonio cloruro) come componente B.
- Aggiungere una determinata concentrazione del componente A all'acqua distillata e mescolare ad alti regimi utilizzando un miscelatore in testa per garantire una corretta miscelazione. Lasciare mescolare per 2-3 minuti.
- Aggiungere una data concentrazione del componente B a questa miscela e lasciare mescolare per altri 2-3 minuti.
- Riposare la miscela per 2-6 ore per sfogare le bolle d'aria. Nota: La miscela di fluidi finali è otticamente trasparente. Per questo studio vengono utilizzate sette miscele di fluidi di diverse concentrazioni. Le concentrazioni sono scelte per ottenere una miscela fluida su un'ampia gamma di viscosità.
2. Misurazione delle velocità di sedimentazione in fluidi illimitati
Vengono utilizzate sfere di vetro di diametro che vanno da 1 a 5 mm.
- Utilizzare un microscopio ad alta risoluzione per misurare il diametro delle sfere di vetro. Assicurarsi che le sfere abbiano superfici lisce e siano sfere quasi perfette.
- Conservare il liquido in contenitori di vetro con diametro almeno 25 volte superiore al diametro delle particelle per assicurarsi che non vi sia alcun effetto delle pareti confinanti sulla velocità di sedimentazione delle particelle.
- Registrare la temperatura ambiente e la temperatura del fluido utilizzando un termometro di laboratorio. La misurazione della temperatura è importante perché le misurazioni reologiche del fluido devono essere effettuate alla temperatura alla quale viene eseguito l'esperimento di sedimentazione.
- Posizionare un bastoncino di misura accanto al contenitore.
- Immergere delicatamente la particella di vetro nel liquido e permettergli di depositarsi. Registrare il processo di assestamento con una videocamera ad alta risoluzione.
- Tenere traccia della posizione della particella in diversi passaggi di tempo dal video registrato utilizzando un'applicazione di analisi delle immagini. Nota: in questo lavoro viene utilizzata un'applicazione software denominata 'Tracker' (http://www.cabrillo.edu/~dbrown/tracker/).
- Tracciare la posizione verticale della particella rispetto al tempo e calcolare la velocità di sedimentazione terminale dalla pendenza della linea.
- Ripetere l'esperimento nell'insieme univoco di condizioni almeno 3 volte per garantire la riproducibilità. Eseguire l'analisi dell'immagine per diverse misurazioni e segnalare la velocità di sedimentazione per un determinato diametro di particelle in un particolare fluido utilizzando barre di errore.
- Ripetere i passaggi precedenti per particelle di diametro diverse e registrare le velocità di sedimentazione. Tracciate la velocità di sedimentazione rispetto al diametro delle particelle. Nota: la figura 1 mostra la velocità di sedimentazione di cinque particelle di dimensioni diverse in un unico fluido.
3. Misurazione delle velocità di sedimentazione per fluidi tra pareti parallele
Per misurare le velocità di sedimentazione in presenza di pareti parallele, vengono utilizzate due cellule sperimentali fatte di plexiglas.
- Durante la progettazione e la costruzione della cella, assicurarsi che le pareti siano lisce e perfettamente parallele l'una all'altra. Mantenere basse le proporzioni delle celle per assicurarsi che non vi sia alcun effetto delle pareti ortogonali sulle pareti parallele. Nota: Lo spazio tra le pareti nelle due cellule in questo studio è rispettivamente di 3,6 mm e 8 mm. La figura 2 mostra uno schema di una cella sperimentale.
- Riempire la cella con il liquido e rilasciare delicatamente la particella nella cella attraverso la porta di ingresso/uscita. Sigillare la porta di ingresso/uscita con un tappo di gomma e lasciare depositare la particella fino a raggiungere il centro della cella.
- A questo punto, posizionare attentamente la cella verticalmente e consentire alla particella di depositarsi.
- Posizionare un bastoncino del contatore accanto alla cella e registrare l'assestamento utilizzando la videocamera ad alta risoluzione.
- Registrare la temperatura ambiente e la temperatura del fluido utilizzando un termometro di laboratorio. Questo è importante perché le misurazioni reologiche del fluido devono essere effettuate a questa temperatura.
- Come per le misurazioni illimitate della velocità di sedimentazione, misurare la velocità di assestamento nell'applicazione software 'Tracker'. Ripetere le misurazioni almeno tre volte per garantire la riproducibilità e ottenere barre di errore su ogni misurazione.
4. Caratterizzazione reologica dei fluidi
- Eseguire le misurazioni costanti della viscosità di taglio per misurare la viscosità del fluido in funzione della velocità di taglio. Nota: In questo lavoro, viene utilizzato il reometro ARES di TA Instruments con un dispositivo cilindrico concentrico a doppia parete (diametro della tazza interna: 27,95 mm, diametro interno del bob: 29,50 mm, diametro del bob esterno: 32,00 mm, diametro della tazza esterna: 34,00 mm, lunghezza del bob: 32,00 mm).
- Variare la velocità di taglio da 0,1-800 sec-1 ed effettuare misurazioni a 10 punti/decennio. Assicurarsi che la temperatura della tazza sia la stessa alla quale è stato eseguito l'esperimento di sedimentazione nello stesso fluido. La figura 3 mostra la viscosità rispetto alla velocità di taglio per un campione di fluido in un grafico log-log.
- Per lo stesso fluido, calcolare l'intervallo di velocità di taglio che le particelle incontrano negli esperimenti di sedimentazione. Utilizzare la velocità media di taglio delle particelle della superficie definita da 2V/dp 20,23, dove V è la velocità di sedimentazione della particella e d pè il diametro della particella.
- Inserire una curva di legge di potenza μ=Kγn-1in questo intervallo di velocità di taglio sulla viscosità rispetto al grafico della velocità di taglio. Su un log-log plot questa vestibilità sarà una linea retta. Determinare i parametri K (indice di coerenza del flusso) e n (indice del comportamento del flusso).
K e n quantificano la viscosità dei fluidi. La figura 3 mostra la legge di potenza adatta alla stessa trama. - Eseguire le misurazioni oscillatorie dinamiche-taglio nell'intervallo di frequenze da 0,1-100 rad/sec e misurare il modulo elastico, G' e il modulo viscoso, G''. Prendi la misurazione a 10 punti/decennio.
La figura 4 mostra la G' e la G'' per un campione di fluido. - Calcolare il rapporto tra i due moduli, G''/G' da questi dati. Adattare il rapporto dei moduli a un modello di Maxwell utilizzando un'analisi di regressione e calcolare iltempo di rilassamento( λ ) del fluido. L'equazione per il rapporto dei due moduli per un modello di Maxwellè 46,47:
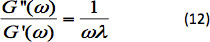
Il tempo di rilassamento del fluido quantifica l'elasticità del fluido. Maggiore è il tempo di rilassamento, più elastico è il fluido. La figura 5 mostra la G''/G' per il campione di fluido insieme all'attacco di Maxwell. Il raccordo viene eseguito riducendo al minimo la somma della misura di varianza nell'intervallo di frequenza.
5. Determinare l'influenza dell'elasticità sulle velocità di assestamento illimitate
- Denotare la velocità di sedimentazione sperimentale di una particella in fluido illimitato di V∞VE dove '∞VE' si riferisce a fluidi viscoelastici non raffinati. Confrontare questa velocità di sedimentazione sperimentale con la velocità di sedimentazione (V∞INEL) calcolata sulla base di dati apparenti di viscosità basati sui parametri della legge di potenza. Usa le espressioni sviluppate da Renaud et al. 1 per calcolare V∞INEL. Le espressioni sono menzionate nella sezione Introduzione. '∞INEL' si riferisce a fluidi anelastiche non raffinati.
- Calcolare il rapporto V∞EL/V∞INEL e fare riferimento al rapporto come rapporto di velocità.
Il valore del rapporto velocità illustra l'influenza dell'elasticità sulla velocità di sedimentazione. Il rapporto velocità maggiore di 1 suggerisce un aumento della velocità/ riduzione della resistenza aerodinamica a causa dell'elasticità del fluido. Il rapporto velocità inferiore a 1 suggerisce un miglioramento della riduzione/trascinamento della velocità dovuto all'elasticità del fluido. - Tracciare il rapporto di velocità in funzione del diametro delle particelle per fluidi diversi per osservare l'effetto dell'elasticità sulla velocità di sedimentazione di particelle di diametro diverso in fluidi di diverse reologie. La figura 6 mostra il rapporto di velocità in funzione del diametro delle particelle in uno dei fluidi.
6. Quantificare l'effetto di ritardo delle pareti parallele sulla risoluzione delle velocità
- Calcolare il fattore della parete, Fw per una data particella di diametro dividendo la velocità di sedimentazione in presenza di pareti parallele, V ∞VE alla velocità di sedimentazione nel fluido illimitato, V∞VE.
- Per un dato fluido, tracciare i fattori della parete in funzione del rapporto tra diametro delle particelle e spaziatura delle pareti, r. La figura 7 mostra i fattori della parete per le particelle che si depositano in uno dei fluidi. La trama aiuta a quantificare l'effetto di ritardo delle pareti confinanti sulla velocità di assestamento. Abbassare il fattore della parete, più alto è l'effetto di ritardo della parete.
Risultati
Gli esperimenti vengono eseguiti per cinque diverse particelle di diametro in sette diverse miscele di fluidi con valori unici K, n e λ. La figura 1 mostra la velocità di sedimentazione in funzione del diametro delle particelle in un fluido. Le barre di errore mostrano la variabilità nelle tre misurazioni. La temperatura ambiente misurata durante l'esperimento è di 23 °C. Si può osservare che le velocità di sedimentazione aumentano con il diametro delle particelle. La figura 3 mostra la misurazione costante della viscosità di taglio per lo stesso fluido eseguita ad una temperatura di 23 °C. La trama mostra la viscosità del fluido in funzione della velocità di taglio. Il fluido mostra un comportamento di assottigliamento della cesoia. Dalle velocità di sedimentazione nella figura 1, le velocità di taglio per tutte le particelle sono calcolate come 2V/dp. In questo intervallo di velocità di taglio, il modello della legge di potenza (K, n) è adatto come mostrato nella figura 3. Il valore di K dall'adattamento è 0,666 Pa.sn e n = 0,31.
La figura 4 mostra il modulo elastico e il modulo viscoso rispetto alla frequenza angolare per lo stesso fluido a 23 °C. La figura 5 mostra il rapporto di G''/G' in funzione della frequenza angolare. È dotato del modello di Maxwell dato dall'equazione 12. La vestibilità è mostrata anche sullo stesso grafico. Il valore del tempo di rilassamento è di 0,175 secondi.
La figura 6 mostra il rapporto di velocità in funzione del diametro delle particelle in uno dei fluidi. Si osserva che il rapporto di velocità è maggiore di uno per le due sfere più piccole e inferiore a uno per le tre sfere più grandi. In altre parole, le sfere più piccole sperimentano una riduzione del trascinamento e le sfere più grandi sperimentano un miglioramento del trascinamento. Ciò suggerisce che l'elasticità del fluido può aumentare o ridurre la velocità di sedimentazione delle sfere. La tabella 2 mostra i numeri di Reynolds per le particelle calcolate utilizzando l'equazione 2. I risultati mostrano che le particelle sperimentano una riduzione/aumento della resistenza aerodinamica a piccoli numeri di Reynolds. Esperimenti simili vengono eseguiti in altri fluidi e si osserva che il rapporto di velocità non è una funzione solo del diametro delle particelle, ma anche delle proprietà reologiche del fluido e della densità delle particelle sferiche. I risultati dettagliati sono disponibili in Malhotra e Sharma43. I lettori dovrebbero vedere la mappa numerica di Drag-Weissenberg Figura 8 a Malhotra e Sharma43. I dati mostrano una riduzione della resistenza aerodinamica a bassi numeri di Weissenberg seguita da una transizione al miglioramento della resistenza aerodinamica ad alti numeri di Weissenberg, anche per le particelle che si depositano nel regime di flusso strisciante (RePL < 0.1).
La figura 7 mostra i fattori della parete (Fw) in funzione del diametro delle particelle e del rapporto di spaziatura tra pareti ( r ),perla sedimentazione della sfera tra pareti parallele di spaziatura di 3,6 mm e 8 mm. I punti dati sono spaziati uniformemente sull'intervallo completo di r che varia da 0 a 1. Si può osservare che i fattori delle pareti diminuiscono con l'aumento del valore di r, suggerendo che gli effetti di ritardo della parete aumentano man mano che il diametro delle particelle diventa paragonabile alla spaziatura delle pareti. Si osserva anche che ad un valore di r, F wnon è unico (a differenza dei fluidi newtoniani) e dipende dalla spaziatura della parete.

Figura 1. Velocità di sedimentazione per particelle di diametro diverso in un fluido VES.

Figura 2. Schema della cella sperimentale utilizzata per misurare le velocità di sedimentazione in presenza di pareti parallele. La cella è fatta di plexiglas e la spaziatura tra le pareti è di 8 mm.

Figura 3. Viscosità in funzione della velocità di taglio per un campione di fluido VES (misurazione costante della viscosità di taglio). La viscosità diminuisce con la velocità di taglio, illustrando un comportamento di assottigliamento della cesoia. La legge di potenza (K, n) inserita nella gamma sperimentale delle velocità di taglio delle particelle è mostrata anche sulla trama.

Figura 4. Modulo elastico(G') e modulo viscoso(G'') in funzione della frequenza angolare per un campione di fluido VES (misura oscillatoria dinamica-taglio).
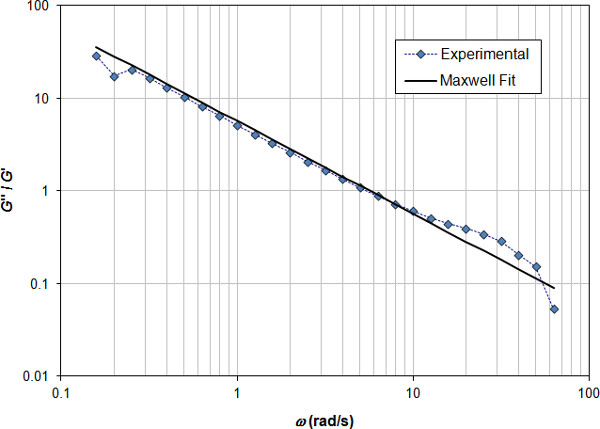
Figura 5. Rapporto tra modulo viscoso ed elastico in funzione della frequenza angolare. L'adattamento di Maxwell viene mostrato sulla trama. Il tempo di rilassamento della vestibilità è di 0,183 sec.
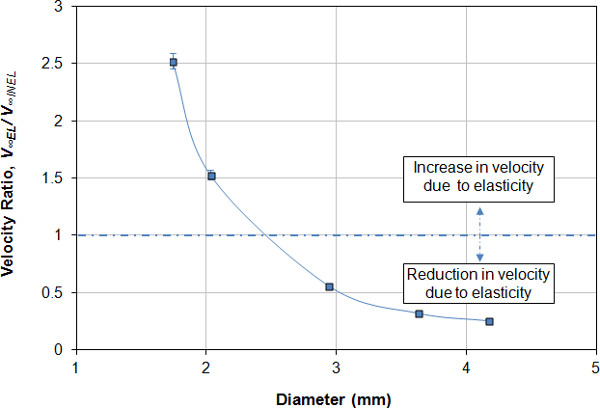
Figura 6. Rapporti di velocità per particelle di dimensioni diverse in un campione di fluido VES. I risultati mostrano che le sfere più piccole sperimentano la riduzione del trascinamento, mentre le particelle più grandi sperimentano il miglioramento della resistenza aerodinamica.
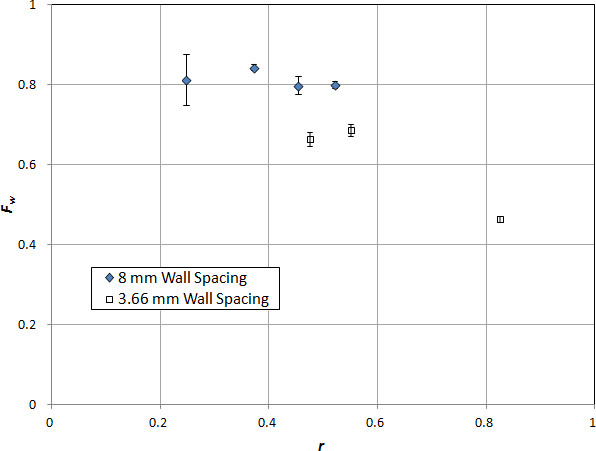
Figura 7. Fattori della parete in funzione del rapporto tra diametro delle particelle e spaziatura delle pareti in un campione di fluido VES. I simboli chiusi si riferiscono ai punti dati per le particelle che si depositano tra pareti con spaziatura di 8 mm e i simboli aperti si riferiscono alla sedimentazione tra pareti con spaziatura di 3,66 mm.
|
Diametro particella ( mm) |
Numero di Reynolds (calcolato utilizzando l'equazione 2) |
| 1.74 | 0.3 |
| 2.03 | 0.44 |
| 2.94 | 1.42 |
| 3.63 | 2.09 |
| 4.17 | 2.63 |
La tabella 2. Numeri di Reynolds per le particelle calcolate usando l'equazione 2.
Discussione
Lo studio sperimentale si concentra sulla misurazione delle velocità di sedimentazione delle particelle sferiche nei fluidi viscoelastici diradante a taglio in condizioni indefinite e confinate. Viene presentata una procedura sperimentale dettagliata per ottenere misurazioni ripetibili delle velocità di sedimentazione. I risultati sono presentati per mostrare che l'elasticità del fluido può aumentare o diminuire la velocità di sedimentazione. Le pareti esercitano un effetto di ritardo sulla sedimentazione e questo effetto è misurato in termini di fattori della parete.
Prima degli esperimenti si dovrebbe garantire che le particelle siano quasi sfere perfette con superfici lisce. Il diametro delle sfere deve essere misurato con precisione. La procedura sperimentale, compresa l'analisi delle immagini, deve essere convalidata eseguendo alcuni esperimenti preliminari su fluidi newtoniani illimitati(ad esempio soluzioni di glicerolo) e confrontando le velocità di sedimentazione sperimentali con le soluzioni analitiche stokes.
Gli esperimenti devono essere ripetuti almeno tre volte per garantire la riproducibilità. Si deve prendere precauzioni perché la temperatura del fluido sia misurata al momento dell'esperimento e che la reologia sia misurata alla stessa temperatura.
Divulgazioni
Gli autori desidera sottolineare che l'obiettivo di questa pubblicazione è la dimostrazione visiva della procedura sperimentale per misurare la sedimentazione delle particelle. Per risultati e analisi particolare particolare vengono esenziati i lettori che devono fare riferimento alla pubblicazioneprecedente 43.
Riconoscimenti
Gli autori sono grati a DOE e RPSEA per il supporto finanziario e alle aziende che sponsorizzano il JIP sulla fratturazione idraulica e il controllo della sabbia presso l'Università del Texas ad Austin (Air Liquide, Air Products, Anadarko, Apache, Baker Hughes, BHP Billiton, BP America, Chevron, ConocoPhillips, ExxonMobil, Ferus, Halliburton, Hess, Linde Group, Pemex, Pioneer Natural Resources , Praxair, Saudi Aramco, Schlumberger, Shell, Southwestern Energy, Statoil, Weatherford e YPF).
Materiali
| Name | Company | Catalog Number | Comments |
| Name of the reagent / equipment | Company | Catalogue number | Comments |
| Glass Microspheres | Whitehouse Scientific | #GP1750 | Available in different sieve fractions. |
| Rheometer | TA Instruments | ARES | Any standard rheometer capable of taking dynamic and static measurements |
| Anionic Surfactant (Component A) | Proprietary fluid | Used in oil field services for hydraulic fracturing. Sodium Xylene Sulfonate can be used as a substitute. | |
| Cationic Surfactant (Component B) | Proprietary fluid | Used in oil field services for hydraulic fractuing. N,N,N-Trimethyl-1-Octadecamonium Chloride can be used as a substitute. |
Riferimenti
- Renaud, M., Mauret, E., Chhabra, R. P. Power-law fluid flow over a sphere: average shear rate and drag. 82, 1066-1070 (2004).
- Clift, R., Grace, J. R., Weber, M. E. . Bubbles, Drops and Particles. , (1978).
- Khan, A. R., Richardson, J. F. The resistance to motion of a solid sphere in a fluid. Chem. Eng. Sci. 62, 135-150 (1987).
- Zapryanov, Z., Tabakova, S. . Dynamics of Bubbles, Drops and Rigid Particles. , (1999).
- Michaelides, E. E., DeKee, D., Chhabra, R. P. Chapter 2. Analytical expressions for the motion of particles. Transport Processes in Bubbles Drops and Particles. , (2002).
- Michaelides, E. E. Hydrodynamic force and heat/mass transfer from particles, bubbles and drops - the Freeman Scholar Lecture. Journal of Fluids Engineering (AMSE. 125, 209-238 (2003).
- Der Faxen, H. Widerstand gegen die Bewegung einer starren Kugel in einer zähen Flüssigkeit, die zwischen zwei parallelen ebenen Wänden eingeschlossen ist). Annalen der Physics. 68, 89-119 (1922).
- Bohlin, T. On the drag on a sphere moving in a viscous fluid inside a cylindrical tube. Trans Royal Insitute of Technology Stockholm. 155, (1960).
- Miyamura, A., Iwasaki, S., Ishii, T. Experimental wall correction factors of single solid spheres in triangular and square cylinders, and parallel plates. International Journal of Multiphase Flow. 7, 41-46 (1981).
- Tullock, D. L., Phan-Thien, N., Graham, A. L. Boundary element simulations of spheres settling in circular, square and triangular ducts. Rheol. Acta. 31, 139-150 (1992).
- Chhabra, R. P. Wall effects on terminal velocity of non-spherical particles in non-Newtonian polymer solutions. Powder Technology. 88, 39-44 (1996).
- Chhabra, R. P., Dekes, D., Chhabra, R. P. Chapter 2. Wall effects on spheres falling axially in cylindrical tubes. Transport Processes in Bubbles Drops and Particles. , (2002).
- Chhabra, R. P., Francis, S. e. c. o. n. d. e. d. .. ,. T. a. y. l. o. r. &. a. m. p. ;. . Bubbles, Drops, and Particles in Non-Newtonian Fluids. , (2007).
- Dazhi, G., Tanner, R. I. The drag on a sphere in a power law fluid. Journal of Non-Newtonian Fluid Mechanics. 17, 1-12 (1984).
- Tripathi, A., Chhabra, R. P., Sundararajan, T. Power-law fluid over spheroidal particles. Industrial & Engineering Chemistry Research. 33, 403-410 (1994).
- Graham, D. I., Jones, T. E. R. Settling and transport of spherical particles in power-law fluids at finite Reynolds number. Journal of Non-Newtonian Fluid Mechanics. 54, 465-488 (1994).
- Tripathi, A., Chhabra, R. P. Drag on spheroidal particles in dilatant fluids. AIChE. 41 (3), 728-731 (1995).
- Missirlis, K. A., Assimacopoulos, D., Mitsoulis, E., Chhabra, R. P. Wall effects for motion of spheres in power-law fluids. Journal of Non-Newtonian Fluid Mechanics. 96 (3), 459-471 (2001).
- Dallon, D. S. . A drag coefficient correlation for spheres settling in Ellis fluids [Ph.D. Dissertation]. , (1967).
- Uhlherr, P. H. T., Le, T. N., Tiu, C. Characterization of inelastic power-law fluids using falling sphere data. Canadian Journal of Chemical Engineering. 54, 497-502 (1976).
- Machac, I., Lecjaks, Z. Wall Effect for a Sphere Falling Through a Non-Newtonian Fluid in a Rectangular Duct. Chemical Engineering Science. 50 (1), 143-148 (1995).
- Kelessidis, V. C., Mpandelis, G. Measurements and prediction of terminal velocity of solid particles falling through stagnant pseudoplastic liquids. Powder Technology. 147, 117-125 (2004).
- Shah, S. N., Fadili, Y. E., Chhabra, R. P. New model for single spherical particle settling velocity in power law (visco-inelastic) fluids. International Journal of Multiphase Flow. 33, 51-66 (2007).
- Rodrigue, D., DeKee, D., Chan Man Fong, C. F. The slow motion of a spherical particle in a Carreau fluid. Chemical Engineering Communications. 154, 203-215 (1996).
- Darby, R. . Chemical Engineering Fluid Mechanics. , (2001).
- Shah, S. N. Proppant settling correlations for non-Newtonian fluids. Society of Petroleum Engineers Journal. 22 (2), 164-170 (1982).
- Shah, S. N. Proppant-settling correlations for non-Newtonian Fluids. Society of Petroleum Engineers Production Engineering Journal. 1 (6), 446-448 (1986).
- Ford, J. T., Oyeneyin, M. B., et al. The formulation of milling fluids for efficient hole cleaning: an experimental investigation. Paper SPE 38819. , (1994).
- Acharya, A., Mashelkar, R. A., Ulbrecht, J. Flow of inelastic and viscoelastic fluids past a sphere, Part II: Anomalous separation in the viscoelastic fluid flow. Rheological Acta. 15, 471-478 (1976).
- Acharya, A. R. Viscoelasticity of crosslinked fracturing fluids and proppant transport. SPE Production Engineering. 3, 483-488 (1988).
- Chhabra, R. P., Uhlherr, P. H. T. Creeping motion of spheres through shear-thinning elastic fluids described by the Carreau viscosity equation. Rheological Acta. 19 (2), 187-195 (1980).
- Bush, M. B., Phan-Thien, N. Drag force on a sphere in creeping motion through a Carreau model fluid. Journal of Non-Newtonian Fluid Mechanics. 16 (3), 303-313 (1984).
- Broadbent, J. M., Mena, B. Slow flow of an elastico-viscous fluid past cylinders and spheres. Chemical Engineering Journal. 8, 11-19 (1974).
- Sigli, D., Coutanceau, M. Effect of finite boundaries on the slow laminar isothermal flow of a viscoelastic fluid around a spherical obstacle. Journal of Non-Newtonian Fluid Mechanics. 2, 1-21 (1977).
- Brule, B. H. A. A. V. D., Gheissary, G. Effects of fluid elasticity on the static and dynamic settling of a spherical particle. Journal of Non-Newtonian Fluid Mechanics. 49, 123-132 (1993).
- Walters, K., Tanner, R. I., Chhabra, R. P. . D. e. K. e. e. ,. D. .. ,., DeKee, D. Chapter 3. The Motion of a Sphere through an Elastic Fluid.. Transport Processes in Bubbles, Drops and Particles. , (1992).
- McKinley, G. H., DeKee, D., Chhabra, R. P. Chapter 14. Steady and transient motion of spherical particles in viscoelastic liquids. Transport Processes in Bubbles, Drops and Particles. , (2002).
- Chhabra, R. P., Tiu, C., Uhlherr, P. H. T. A study of wall effects on the motion of a sphere in viscoelastic fluids. Canadian Journal of Chemical Engineering. 59, 771-775 (1981).
- Jones, W. M., Price, A. H., Walters, K. The motion of a sphere falling under gravity in a constant viscosity elastic liquid. Journal of Non-Newtonian Fluid Mechanics. 53, 175-196 (1994).
- Navez, V., Walters, K. A note on settling in shear-thinning polymer solutions. Journal of Non-Newtonian Fluid Mechanics. 67, 325-334 (1996).
- Huang, P. Y., Wall Feng, J. effects on the flow of viscoelastic fluids around a circular cylinder. Journal of Non-Newtonian Fluid Mechanics. 60, 179-198 (1995).
- Sugeng, F., Tanner, R. I. The drag on spheres in viscoelastic fluids with significant wall effects. Journal of Non-Newtonian Fluid Mechanics. 20, 281-292 (1986).
- Malhotra, S., Sharma, M. M. Settling of Spherical Particles in Unbounded and Confined Surfactant-Based Shear Thinning Viscoelastic Fluids: An Experimental Study. Chemical Engineering Science. 84, 646-655 (2012).
- Zhang, K. Fluids for Fracturing Subterranean Formations.U.S. US patent. , (2002).
- Gupta, D. V. S., Leshchyshyn, T. T., Hlidek, B. T. Surfactant gel foam/emulsions: History and field application in the western Canadian sedimentary basin. , (2005).
- Ferry, J. D. . Viscoelastic Properties of Polymers. , (1970).
- Yesilata, B., Clasen, C., McKinley, G. H. Nonlinear shear and extensional Flow dynamics of wormlike surfactant solutions. Journal of Non-Newtonian Fluid Mechanics. 133, 73-90 (2006).
Ristampe e Autorizzazioni
Richiedi autorizzazione per utilizzare il testo o le figure di questo articolo JoVE
Richiedi AutorizzazioneThis article has been published
Video Coming Soon