Method Article
תהליך עבודה לאופטימיזציה של נוסחת ננו-חלקיקי שומנים (LNP) באמצעות ניסויים מתוכננים בתהליך תערובות ומודלים של אנסמבל מאומת עצמי (SVEM)
In This Article
Summary
פרוטוקול זה מספק גישה לאופטימיזציה של ניסוח על פני גורמי מחקר מתערובת, רציפים וקטגוריים הממזערת בחירות סובייקטיביות במבנה התכנון הניסויי. בשלב הניתוח נעשה שימוש בהליך התאמת מידול יעיל וקל לשימוש.
Abstract
אנו מציגים גישה בסגנון איכות לפי עיצוב (QbD) לאופטימיזציה של נוסחאות ננו-חלקיקי שומנים (LNP), במטרה להציע למדענים זרימת עבודה נגישה. המגבלה המובנית במחקרים אלה, שבהם היחסים המולריים של שומנים מיוננים, מסייעים ו-PEG חייבים להצטבר עד 100%, דורשת שיטות תכנון וניתוח מיוחדות כדי להתאים לאילוץ תערובת זה. תוך התמקדות בגורמי שומנים ותהליכים המשמשים בדרך כלל באופטימיזציה של תכנון LNP, אנו מספקים צעדים המונעים רבים מהקשיים המתעוררים באופן מסורתי בתכנון וניתוח של ניסויי תהליך תערובות על ידי שימוש בעיצובים ממלאים חלל וניצול המסגרת הסטטיסטית שפותחה לאחרונה של מודלי אנסמבל מאומתים עצמיים (SVEM). בנוסף להפקת ניסוחים אופטימליים למועמדים, זרימת העבודה בונה גם סיכומים גרפיים של המודלים הסטטיסטיים המותאמים המפשטים את פרשנות התוצאות. ניסוחי המועמדים החדשים שזוהו מוערכים באמצעות ריצות אישור ולחלופין ניתן לבצע אותם בהקשר של מחקר מקיף יותר בשלב השני.
Introduction
ניסוחים של ננו-חלקיקי ליפידים (LNP) עבור מערכות העברת גנים in vivo כוללות בדרך כלל ארבעה ליפידים מרכיבים מהקטגוריות של ליפידים מיוננים, עוזרים ו-PEG 1,2,3. בין אם ליפידים אלה נחקרים לבד או בו זמנית עם גורמים אחרים שאינם תערובת, ניסויים עבור ניסוחים אלה דורשים עיצובי "תערובת" מכיוון - בהינתן ניסוח מועמד - הגדלת או הקטנת היחס בין כל אחד מהליפידים מובילה בהכרח לירידה או עלייה מקבילה בסכום היחסים של שלושת הליפידים האחרים.
לשם המחשה, ההנחה היא שאנחנו מייעלים ניסוח LNP שכרגע משתמש במתכון מוגדר שיטופל כאמת המידה. המטרה היא למקסם את העוצמה של LNP תוך שאיפה משנית למזער את גודל החלקיקים הממוצע. גורמי המחקר המגוונים בניסוי הם היחסים המולריים של ארבעת השומנים המרכיבים (מיוננים, כולסטרול, DOPE, PEG), יחס N:P, קצב הזרימה וסוג השומנים המיוננים. השומנים המיוננים והמסייעים (כולל כולסטרול) מורשים להשתנות בטווח רחב יותר של יחס מולארי, 10-60%, מאשר PEG, אשר ישתנה בין 1-5% באיור זה. מתכון ניסוח אמת המידה והטווחים של הגורמים האחרים וגרעיניות העיגול שלהם מפורטים בקובץ משלים 1. לדוגמה זו, המדענים מסוגלים לבצע 23 ריצות (קבוצות ייחודיות של חלקיקים) ביום אחד ורוצים להשתמש בו כגודל הדגימה שלהם אם הוא עומד בדרישות המינימום. תוצאות סימולציה של ניסוי זה מופיעות בקובץ משלים 2 ובקובץ משלים 3.
Rampado ו-Peer4 פרסמו לאחרונה מאמר סקירה בנושא ניסויים מתוכננים לאופטימיזציה של מערכות אספקת תרופות מבוססות ננו-חלקיקים. Kauffman et al.5 שקלו מחקרי אופטימיזציה של LNP באמצעות עיצובי סינון חלקיים וסופיים6; עם זאת, סוגים אלה של עיצובים אינם יכולים להתאים לאילוץ תערובת מבלי להזדקק לשימוש ב"משתני רפיון" לא יעילים7 ואינם משמשים בדרך כלל כאשר גורמי תערובת קיימים 7,8. במקום זאת, "עיצובים אופטימליים" המסוגלים לשלב אילוץ תערובת משמשים באופן מסורתי לניסויים בתהליך תערובות9. עיצובים אלה מכוונים לפונקציה שצוינה על-ידי המשתמש של גורמי המחקר והם אופטימליים (באחד ממספר מובנים אפשריים) רק אם פונקציה זו לוכדת את הקשר האמיתי בין גורמי המחקר ותגובותיהם. יש לשים לב כי קיימת הבחנה בטקסט בין "עיצובים אופטימליים" לבין "מועמדים לניסוח אופטימלי", כאשר האחרון מתייחס לניסוחים הטובים ביותר המזוהים על ידי מודל סטטיסטי. עיצובים אופטימליים מגיעים עם שלושה חסרונות עיקריים לניסויים בתהליך תערובת. ראשית, אם המדען אינו מצליח לצפות אינטראקציה של גורמי המחקר בעת ציון מודל היעד, אז המודל המתקבל יהיה מוטה ויכול לייצר ניסוחים מועמדים נחותים. שנית, עיצובים אופטימליים מציבים את רוב הריצות על הגבול החיצוני של חלל הפקטור. במחקרי LNP, זה יכול להוביל למספר רב של ריצות אבודות אם החלקיקים אינם נוצרים כראוי בכל הקצוות של הגדרות השומנים או התהליך. שלישית, מדענים מעדיפים לעתים קרובות לערוך ריצות ניסוי על פנים מרחב הגורמים כדי לקבל תחושה בלתי תלויה במודל של משטח התגובה ולצפות בתהליך ישירות באזורים שלא נחקרו בעבר במרחב הגורמים.
עיקרון תכנון חלופי הוא לכוון לכיסוי אחיד משוער של מרחב הגורם (מוגבל התערובת) עם עיצוב ממלא חלל10. עיצובים אלה מקריבים יעילות ניסויית מסוימת ביחס לעיצובים אופטימליים9 (בהנחה שכל מרחב הגורמים מוביל לניסוחים תקפים) אך מציגים מספר יתרונות בפשרה שהם שימושיים ביישום זה. תכנון מילוי החלל אינו מניח הנחות אפריוריות לגבי מבנה משטח התגובה; זה נותן לו את הגמישות ללכוד יחסים בלתי צפויים בין גורמי המחקר. זה גם מייעל את יצירת העיצוב מכיוון שהוא אינו דורש קבלת החלטות לגבי אילו מונחי רגרסיה להוסיף או להסיר כאשר גודל הריצה הרצוי מותאם. כאשר נקודות עיצוב מסוימות (מתכונים) מובילות לניסוחים כושלים, עיצובים ממלאים מקום מאפשרים למדל את גבול הכשל מעל גורמי המחקר תוך תמיכה במודלים סטטיסטיים לתגובות המחקר על פני שילובי הגורמים המוצלחים. לבסוף, הכיסוי הפנימי של מרחב הגורמים מאפשר חקירה גרפית בלתי תלויה במודל של משטח התגובה.
כדי לדמיין את תת-המרחב של גורם התערובת של ניסוי תערובת-תהליך, נעשה שימוש ב"חלקות טרינריות" משולשות מיוחדות. איור 1 מניע את השימוש הזה: בקובייה של נקודות שבהן מאפשרים לכל אחד שלושה מרכיבים לנוע בין 0 ל-1, הנקודות שמקיימות אילוץ שסכום המרכיבים שווה ל-1 מסומנות באדום. אילוץ התערובת על שלושת המרכיבים מקטין את שטח הגורם האפשרי למשולש. ביישומי LNP עם ארבעה מרכיבי תערובת, אנו מייצרים שש חלקות טרינריות שונות המייצגות את מרחב הגורמים על ידי התוויית שני ליפידים בכל פעם כנגד ציר "אחרים" המייצג את סכום הליפידים האחרים.

איור 1: אזורי גורם משולש. בחלקת מילוי החלל בתוך הקובייה, הנקודות האפורות הקטנות מייצגות ניסוחים שאינם עולים בקנה אחד עם אילוץ התערובת. הנקודות האדומות הגדולות יותר מונחות על משולש החקוק בתוך הקובייה ומייצגות ניסוחים שעבורם אילוץ התערובת מסופק. אנא לחץ כאן כדי להציג גרסה גדולה יותר של איור זה.
בנוסף לגורמי תערובת השומנים, לעתים קרובות ישנם גורם תהליך רציף אחד או יותר כגון יחס N:P, ריכוז חיץ או קצב זרימה. גורמים קטגוריים עשויים להיות נוכחים, כגון סוג שומנים מיוננים, סוג שומנים עוזר או סוג חיץ. המטרה היא למצוא נוסחה (תערובת של שומנים והגדרות לגורמי תהליך) שממקסמת מידה מסוימת של עוצמה ו/או משפרת מאפיינים פיזיוכימיים כגון מזעור גודל החלקיקים וה-PDI (מדד פיזור רב), מקסום אחוזי הקפסולה, וממזערת תופעות לוואי - כגון ירידה במשקל הגוף - במחקרי in vivo . גם כאשר מתחילים ממתכון בנצ'מרק סביר, ייתכן שיהיה עניין באופטימיזציה מחדש בהינתן שינוי במטען הגנטי או כאשר שוקלים שינויים בגורמי התהליך או בסוגי השומנים.
קורנל7 מספק טקסט סופי על ההיבטים הסטטיסטיים של ניסויי תערובות ותערובת-תהליך, כאשר מאיירס ואחרים 9 מספקים סיכום מצוין של נושאי תכנון וניתוח התערובת הרלוונטיים ביותר לאופטימיזציה. עם זאת, עבודות אלה יכולות להעמיס על מדענים פרטים סטטיסטיים ועם טרמינולוגיה מיוחדת. תוכנה מודרנית לתכנון וניתוח ניסויים מספקת פתרון חזק שיתמוך מספיק ברוב בעיות האופטימיזציה של LNP מבלי לפנות לתיאוריה הרלוונטית. בעוד שמחקרים מסובכים יותר או בעלי עדיפות גבוהה עדיין יפיקו תועלת משיתוף פעולה עם סטטיסטיקאי ועשויים להשתמש בעיצובים אופטימליים ולא ממלאים מקום, מטרתנו היא לשפר את רמת הנוחות של מדענים ולעודד אופטימיזציה של פורמולציות LNP מבלי לפנות לבדיקות לא יעילות של גורם אחד בכל פעם (OFAT)11 או פשוט להסתפק בנוסחה הראשונה העונה על המפרטים.
במאמר זה, מוצגת זרימת עבודה המשתמשת בתוכנה סטטיסטית כדי לייעל בעיית ניסוח LNP גנרית, ומטפלת בבעיות תכנון וניתוח לפי הסדר שבו הן ייתקלו בהן. למעשה, השיטה תעבוד עבור בעיות אופטימיזציה כלליות ואינה מוגבלת ל- LNPs. לאורך הדרך מטופלות מספר שאלות נפוצות שעולות וניתנות המלצות המעוגנות בניסיון ובתוצאות סימולציה12. המסגרת שפותחה לאחרונה של מודלים של אנסמבל מאומת עצמית (SVEM)13 שיפרה מאוד את הגישה השברירית לניתוח תוצאות מניסויים בתהליך תערובת, ואנו משתמשים בגישה זו כדי לספק אסטרטגיה פשוטה יותר לאופטימיזציה של פורמולציה. בעוד זרימת העבודה בנויה באופן כללי שניתן לעקוב אחריו באמצעות חבילות תוכנה אחרות, JMP 17 Pro ייחודי בכך שהוא מציע SVEM יחד עם כלי הסיכום הגרפיים שמצאנו כנחוצים כדי לפשט את הניתוח הארכאי של ניסויים בתהליך תערובת. כתוצאה מכך, הוראות ספציפיות JMP מסופקות גם בפרוטוקול.
SVEM משתמש באותו בסיס מודל רגרסיה ליניארית כמו הגישה המסורתית, אך הוא מאפשר לנו להימנע משינויים מייגעים הנדרשים כדי להתאים ל"מודל מלא" של השפעות מועמדים באמצעות בחירת קדימה או גישת בסיס בחירה נענשת (לאסו). בנוסף, SVEM מספק התאמת "מודל מופחת" משופרת הממזערת את הפוטנציאל לשילוב רעש (תהליך בתוספת שונות אנליטית) המופיע בנתונים. זה עובד על ידי ממוצע המודלים החזויים הנובעים משקלול חוזר ונשנה של החשיבות היחסית של כל ריצה במודל 13,14,15,16,17,18. SVEM מספק מסגרת למידול ניסויים בתהליך תערובת, שהיא גם קלה יותר ליישום מאשר רגרסיה מסורתית של ירייה בודדת וגם מניבה מועמדים לניסוח אופטימלי באיכות טובה יותר12,13. הפרטים המתמטיים של SVEM הם מעבר להיקף של מאמר זה ואפילו סיכום שטחי מעבר לסקירת הספרות הרלוונטית יסיח את הדעת מהיתרון העיקרי שלו ביישום זה: הוא מאפשר הליך פשוט, חזק ומדויק של לחץ והפעל עבור מתרגלים.
זרימת העבודה המוצגת עולה בקנה אחד עם גישת איכות לפי עיצוב (QbD)19 לפיתוח תרופות20. תוצאת המחקר תהיה הבנה של הקשר הפונקציונלי המקשר בין תכונות החומר ופרמטרי התהליך לתכונות איכות קריטיות (CQAs)21. דניאל ואחרים 22 דנים בשימוש במסגרת QbD במיוחד לייצור פלטפורמת RNA: זרימת העבודה שלנו יכולה לשמש ככלי במסגרת זו.
Protocol
הניסוי המתואר בסעיף התוצאות המייצגות בוצע בהתאם למדריך לטיפול ושימוש בחיות מעבדה והנהלים בוצעו בהתאם להנחיות שנקבעו על ידי הוועדה המוסדית לטיפול ושימוש בבעלי חיים (IACUC). נקבות עכברי Balb/C בנות 6-8 שבועות הושגו באופן מסחרי. בעלי החיים קיבלו צ'או ומים סטנדרטיים ושוכנו בתנאים סטנדרטיים עם מחזורי אור / חושך של 12 שעות, בטמפרטורה של 65-75 ° F (~ 18-23 ° C) עם 40-60% לחות.
1. רישום מטרת המחקר, תגובותיו וגורמים
הערה: לאורך פרוטוקול זה, JMP 17 Pro משמש לתכנון וניתוח הניסוי. ניתן להשתמש בתוכנה מקבילה בעקבות שלבים דומים. לקבלת דוגמאות והוראות נוספות לכל השלבים שבוצעו בסעיף 1, עיין בקובץ משלים 1.
- סכם את מטרת הניסוי במסמך עם חותמת תאריך.
- פרט את התגובות הראשוניות (CQAs) שיימדדו במהלך הניסוי.
- פרט תגובות משניות (למשל, הגבלות במורד הזרם על תכונות פיזיוכימיות) שניתן למדוד.
- פרט פרמטרים של תהליך שעשויים להיות קשורים לתשובות, כולל אלה הרלוונטיים ביותר למטרת המחקר.
- אם המחקר יתפרש על פני מספר ימים, כלול גורם "חסימה" קטגורי של יום.
הערה: פעולה זו מאזנת את הגדרות הגורמים בין ימים כדי למנוע בלבול בין שינויים ברמת היום בתהליך לבין גורמי המחקר. - בחר את הגורמים להיות מגוונים ואת אלה שיש לשמור קבוע במהלך המחקר.
הערה: השתמש בכלי תעדוף סיכונים כגון ניתוח אפקטים של מצב כשל20 לבחירת קבוצת המשנה הרלוונטית ביותר של גורמים (איור 2). בדרך כלל, כל השומנים צריכים להיות מותרים להשתנות; למרות שבמקרים מסוימים מוגבלים בתקציב, סביר לנעול PEG ביחס קבוע. - קבע את הטווחים עבור הגורמים השונים ואת הדיוק העשרוני הרלוונטי עבור כל אחד מהם.
- החליטו על גודל תכנון המחקר (מספר קבוצות החלקיקים הייחודיות) תוך שימוש בהיוריסטיקות המינימליות והמקסימליות. ריצות השוואת ביצועים של בקרה הכלולות באופן ידני אינן נכללות בגודל הריצה המומלץ על-ידי ההיוריסטיקה.
הערה: ההיוריסטיקות הבאות מניחות שהתגובות רציפות. ההיוריסטיקה המינימלית מניחה שניתן יהיה לבצע מחקר המשך, במידת הצורך, בנוסף לביצוע ריצות אישור לניסוחים אופטימליים של מועמדים. אם זה יהיה ריאלי רק לבצע ריצות אישור, אז עדיף לתקצב את מספר הריצות המתקבלות מן היוריסטיקה מקסימלית. עבור תגובות בינאריות ראשוניות, בקש עזרה מסטטיסטיקאי כדי לקבוע את מספר הריצות המתאים.- היוריסטיקה מינימלית: הקצו שלוש ריצות לכל גורם תערובת, שתיים לכל גורם תהליך רציף, ואחת לכל רמה של כל גורם קטגורי.
הערה: עבור מחקר עם ארבעה גורמי שומנים, שניים רציפים ואחד משתנה תהליך קטגורי תלת-כיווני, זה מוביל להצעה של (3 x 4) + (2 x 2) + 3=19 ריצות מילוי חלל. הוסף הפעלות נוספות אם סביר להניח שחלקן ייכשלו עקב בעיות ניסוח או מדידה. - היוריסטיקה מרבית: הפעל את התוכנה לבניית עיצובים אופטימליים והזן את הפרמטרים הדרושים להזמנה שנייה (כולל אפקטים עיקריים, אינטראקציות דו-כיווניות בין כל האפקטים, ואפקטים ריבועיים לגורמי תהליך רציפים). חשב את גודל ההפעלה המינימלי בהתאם לאלגוריתם של התוכנה. הוסף 1 לתוצאה המתקבלת מהתוכנה כדי להגדיר את ההיוריסטיקה המקסימלית.
הערה: עיין בקובץ משלים 1 לקבלת הוראות מפורטות לביצוע שלבים אלה. מקרה לדוגמה עם ארבעה גורמי שומנים, שניים רציפים ואחד משולש משתנה תהליך קטגורי, מוביל לגודל ריצה מומלץ של 34 (33 מהמלצת תוכנה + 1). סביר להניח שכל ריצה מעבר לכך תשמש טוב יותר לאישור או למחקרי המשך.
- היוריסטיקה מינימלית: הקצו שלוש ריצות לכל גורם תערובת, שתיים לכל גורם תהליך רציף, ואחת לכל רמה של כל גורם קטגורי.
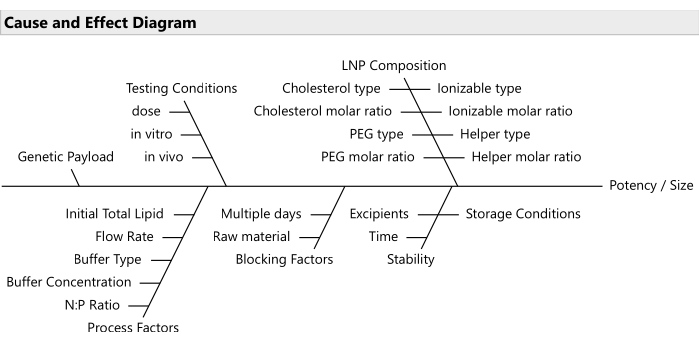
איור 2: דיאגרמת סיבה ותוצאה. הדיאגרמה מציגה גורמים נפוצים בבעיית אופטימיזציה של ניסוח LNP. אנא לחץ כאן כדי להציג גרסה גדולה יותר של איור זה.
2. יצירת שולחן עיצוב בעיצוב ממלא מקום
- פתח את JMP ונווט בשורת התפריטים אל DOE > Special Purpose > Space Filling Design.
- הזן את תשובות המחקר (ראה קובץ משלים 1).
- אופציונלי: הוסף עמודות עבור תגובות נוספות, המציינות אם יש להגדיל, למזער או למקד כל אחת מהן על-ידי לחיצה על הוסף תגובה.
הערה: ניתן לשנות הגדרות אלה מאוחר יותר ואינן משפיעות על העיצוב. כמו כן, ניתן להוסיף עמודות נוספות לתגובות נוספות לאחר יצירת טבלת העיצוב. - הזן את גורמי המחקר ואת הטווחים המתאימים. השתמשו בלחצן ' ערבוב ' להוספת גורמי מיזוג, בלחצן 'רציף' להוספת גורמים רציפים , או בלחצן 'קטגוריות ' להוספת גורמים קטגוריים.
הערה: מחקר לדוגמה זה משתמש בגורמים ובטווחים המתוארים באיור 3, הכוללים את היחס המולרי המיונן (הנע בין 0.1 ל-0.6), היחס המולרי המסייע (גם הוא בין 0.1 ל-0.6), היחס המולרי כולסטרול (בין 0.1 ל-0.6), היחס המולרי PEG (בין 0.01 ל-0.05) וסוג השומנים המיוננים (שיכול להיות H101, H102, או H103). - הזן את מספר ההפעלות שנקבע מראש עבור העיצוב לשדה מספר הפעלות .
- אופציונלי: הגדל את גודל האשכול הממוצע מברירת המחדל של 50 ל- 2000 באמצעות תפריט המשולש האדום לצד הכותרת עיצוב מילוי שטח ובתפריט המשנה אפשרויות מתקדמות .
הערה: זוהי הגדרה עבור אלגוריתם מילוי החלל שיכולה להוביל לבניית תכנון מעט טובה יותר במחיר של זמן חישובי נוסף. - צור את טבלת העיצוב הממלאת את החלל עבור הגורמים שנבחרו וגודל ההפעלה. לחץ/י על ״מילוי גמיש מהיר״ ולאחר מכן לחץ/י על ״ צור טבלה״.
הערה: שתי הריצות הראשונות מעיצוב לדוגמה מוצגות באיור 4. - הוסף עמודת הערות לטבלה כדי להוסיף ביאורים להפעלות שנוצרו באופן ידני. לחץ פעמיים על כותרת העמודה הריקה הראשונה כדי להוסיף עמודה ולאחר מכן לחץ פעמיים על כותרת העמודה החדשה כדי לערוך את השם.
- אם ישים, שלב באופן ידני פקדי ביצועים בטבלת העיצוב. כלול עותק משוכפל עבור אחד מאמות המידה של הבקרה. סמן את שם אמת המידה בעמודה הערות וקודד בצבע את השוואת הביצועים שכפל שורות לזיהוי קל של תרשים.
- הוסף שורה חדשה על-ידי לחיצה כפולה על כותרת השורה הריקה הראשונה והזן את הגדרות גורם ההשוואה. שכפל שורה זו כדי ליצור שכפול של אמת המידה. סמן את שתי השורות ונווט אל שורות > צבעים כדי להקצות צבע למטרות יצירת תרשימים.
הערה: השכפול מספק הערכה שאינה תלויה במודל של התהליך בתוספת שונות אנליטית ויספק תובנה גרפית נוספת.
- הוסף שורה חדשה על-ידי לחיצה כפולה על כותרת השורה הריקה הראשונה והזן את הגדרות גורם ההשוואה. שכפל שורה זו כדי ליצור שכפול של אמת המידה. סמן את שתי השורות ונווט אל שורות > צבעים כדי להקצות צבע למטרות יצירת תרשימים.
- אם כל ריצת בקרת ביצועים חורגת מהטווח של גורמי המחקר, ציין זאת בעמודה "הערות" להדרה עתידית מהניתוח.
- עיגלו את גורמי התערובת לרמת הפירוט המתאימה. לשם כך,
- סמן את כותרות העמודות עבור גורמי התערובת, לחץ באמצעות לחצן העכבר הימני על אחת מכותרות העמודות ונווט אל עמודת נוסחה חדשה > המרה > סבב..., הזן את מרווח הזמן הנכון לעיגול ולחץ על אישור.
- ודא שלא נבחרו שורות על-ידי לחיצה על המשולש התחתון בהצטלבות כותרות השורות והעמודות.
- העתק את הערכים מהעמודות המעוגלות החדשות שנוצרו (Ctrl + C) והדבק (Ctrl + V) בעמודות התערובת המקוריות. לבסוף, מחק את עמודות הערך המעוגל הזמניות.
- לאחר עיגול יחסי השומנים, ודא שהסכום שלהם שווה ל- 100% על-ידי בחירת כותרות העמודות עבור גורמי התערובת, לחיצה באמצעות לחצן העכבר הימני על אחד מהם ומעבר אל עמודת נוסחה חדשה > שלב סכום >. אם סכום של שורה כלשהי אינו שווה ל- 1, התאם ידנית אחד מגורמי התערובת, כדי להבטיח שהגדרת הגורמים תישאר בטווח הגורמים. מחק את עמודת הסכום לאחר ביצוע ההתאמות.
- בצע את אותו הליך המשמש לעיגול גורמי התערובת כדי לעגל את גורמי התהליך לרמת הפירוט המתאימה שלהם.
- עצבו את עמודות השומנים כך שיוצגו כאחוזים עם מספר הנקודות העשרוניות הרצוי: בחרו בכותרות העמודות, לחצו לחיצה ימנית ובחרו 'תקנן תכונות...'. בחלון הבא, הגדר את עיצוב לאחוזים והתאם את מספר המספרים העשרוניים לפי הצורך.
- אם נוספו הפעלות ידניות, כגון אמות מידה, סדר מחדש את סדר השורות בטבלה: הוסף עמודה חדשה עם ערכים אקראיים (לחץ באמצעות לחצן העכבר הימני על כותרת העמודה האחרונה ובחר עמודת נוסחה חדשה > אקראי > אקראי רגיל). מיין עמודה זו בסדר עולה על-ידי לחיצה באמצעות לחצן העכבר הימני על כותרת העמודה שלה ולאחר מכן מחק את העמודה.
- אופציונלי: הוסף עמודה מזהה הפעלה . אכלס זאת בתאריך הנוכחי, בשם הניסוי ובמספר השורה מהטבלה.
הערה: ראה (איור 5) לדוגמה. - צרו חלקות טרינריות כדי להמחיש את נקודות העיצוב מעל גורמי השומנים (איור 6). כמו כן, בחנו את התפלגות הריצה על פני גורמי התהליך (איור 7): בחרו Graph > Ternary Plot. בחר רק את גורמי התערובת עבור X, התוויית.
- כדי לבחון את ההתפלגות על פני גורמי התהליך, בחר נתח התפלגות > והזן את גורמי התהליך עבור Y, עמודות.
הערה: מדען הניסוח צריך לאשר את ההיתכנות של כל הריצות. אם קיימות ריצות בלתי ישימות, הפעל מחדש את העיצוב בהתחשב באילוצים החדשים שהתגלו.

איור 3: גורמי המחקר והטווחים. צילומי מסך של הגדרות בתוך תוכנות ניסיוניות שימושיים לשחזור מערך המחקר. אנא לחץ כאן כדי להציג גרסה גדולה יותר של איור זה.

איור 4: פלט ראשוני לתכנון ממלא חלל. הצגת שתי השורות הראשונות של הטבלה, יש לעגל את ההגדרות לדיוק הרצוי תוך הקפדה על כך שכמויות השומנים מסתכמות ב- 1. אמת המידה נוספה לטבלה באופן ידני. אנא לחץ כאן כדי להציג גרסה גדולה יותר של איור זה.

איור 5: טבלת לימוד מעוצבת. רמות הגורמים עוגלו ועוצבו ונוספה עמודה Run ID. אנא לחץ כאן כדי להציג גרסה גדולה יותר של איור זה.

איור 6: נקודות עיצוב על חלקה טרינרית. 23 הפורמולציות מוצגות כפונקציה של היחס המקביל בין Ionizable, Helper ו-"Others" (כולסטרול+PEG). הנקודה הירוקה במרכז מייצגת את אמת המידה 33:33:33:1 יחס מולארי של Ionizable (H101):כולסטרול:עוזר (DOPE):P EG. אנא לחץ כאן כדי להציג גרסה גדולה יותר של איור זה.

איור 7: התפלגות גורמי תהליך שאינם תערובת בניסוי. ההיסטוגרמות מראות כיצד ריצות הניסוי מפוזרות על פני סוג שומנים מיוננים, יחס N:P וקצב זרימה. אנא לחץ כאן כדי להציג גרסה גדולה יותר של איור זה.
3. הפעלת הניסוי
- הפעל את הניסוי בסדר שסופק על-ידי טבלת העיצוב. הקלט את הקריאות בעמודות המובנות בטבלת הניסויים.
- אם מבוצעות בדיקות מרובות עבור אותה תגובה באצוות נוסחה זהה, חשב ממוצע עבור תוצאות אלה בכל אצווה. הוסף עמודה עבור כל מדידת בדיקה לטבלה.
- לקבלת ממוצע, בחר את כל העמודות הקשורות, לחץ באמצעות לחצן העכבר הימני על אחת מכותרות העמודות שנבחרו ובחר עמודת נוסחה חדשה > שלב > ממוצע. השתמש בעמודה Average זו לניתוח תגובות עתידיות.
הערה: מבלי להתחיל את המתכון מחדש, מדידות בדיקה חוזרות רק לוכדות שונות בבדיקה ואינן מהוות שכפול עצמאי.
- לקבלת ממוצע, בחר את כל העמודות הקשורות, לחץ באמצעות לחצן העכבר הימני על אחת מכותרות העמודות שנבחרו ובחר עמודת נוסחה חדשה > שלב > ממוצע. השתמש בעמודה Average זו לניתוח תגובות עתידיות.
- תעד כל התרחשות של משקעי ניסוח או בעיות סבילות in vivo (כגון ירידה חמורה במשקל הגוף או מוות) עם אינדיקטורים בינאריים (0/1) בעמודה חדשה עבור כל סוג של בעיה.
4. ניתוח תוצאות הניסוי
- התווה את הקריאות ובחן את התפלגות התגובות: פתח את Graph > Graph Builder וגרור כל תגובה לאזור Y עבור חלקות בודדות. חזור על פעולה זו עבור כל התגובות.
- בדוק את המרחק היחסי בין הריצות המשוכפלות המסומנות בצבעים, אם נכללו בהן. הדבר מאפשר להבין את השונות הכוללת (התהליכית והאנליטית) בבנצ'מרק בהשוואה לשונות הנובעת משינויים בהגדרות הגורמים על פני כל מרחב הגורמים (איור 8).
- קבע אם יש למדל את התגובה הגולמית או אם יש להשתמש בשינוי צורה במקום זאת. עבור תגובות המוגבלות להיות חיוביות אך אינן מוגבלות לעיל (למשל, עוצמה), התאימו הן התפלגות נורמלית והן התפלגות לוגנורמלית לתוצאות הניסוי. אם ההתפלגות הלוג-נורמלית מתאימה יותר ל-AICc נמוך יותר (קריטריון המידע של Akaike מתוקן), בצע טרנספורמציית יומן של תגובה זו.
- נווט אל נתח התפלגות > ובחר את התגובה עבור Y, עמודות. בדוח ההתפלגות המתקבל, לחץ על המשולש האדום לצד שם התגובה ובחר Continuous Fit > Fit Normal ו- Continuous Fit > Fit Lognormal מהתפריט הנפתח. בדוח השוואת ההתפלגויות הבא, בדוק את ערכי AICc כדי לוודא איזו התפלגות מתאימה יותר לתגובה.
- כדי לבצע המרת יומן רישום, לחץ באמצעות לחצן העכבר הימני על כותרת עמודת התגובה ובחר עמודת נוסחה חדשה > יומן > יומן רישום. כאשר מודל נבנה ועמודת חיזוי בסולם יומן הרישום נשמרת, המר את התגובה בחזרה לקנה המידה המקורי על-ידי בחירה באפשרות עמודת נוסחה חדשה > יומן > Exp.
- עבור תגובות פרופורציה התחומות בין 0 ל- 1, השווה את ההתאמה של התפלגות נורמלית והתפלגות ביתא. אם להתפלגות הביתא יש AICc נמוך יותר, בצע המרת logit. בדוח ההתפלגות עבור התגובה, בחר Continuous Fit > Fit Normal ו - Continuous Fit >- Fit Beta.
- להמרת logit, לחץ באמצעות לחצן העכבר הימני על כותרת עמודת התגובה בטבלת הנתונים ובחר New Formula Column > Specialty > Logit. לאחר בניית מודל, שמור את עמודת החיזוי. כדי לחזור לקנה המידה המקורי, השתמש בעמודת נוסחה חדשה > לוגיסטיקה > מיוחדות.
הערה: ניתוח SVEM מבוסס רגרסיה עמיד בפני חריגות מהנורמליות בהתפלגות התגובה. עם זאת, שינויים אלה יכולים להוביל לפרשנות קלה יותר של התוצאות ולהתאמה משופרת של המודלים.
- להמרת logit, לחץ באמצעות לחצן העכבר הימני על כותרת עמודת התגובה בטבלת הנתונים ובחר New Formula Column > Specialty > Logit. לאחר בניית מודל, שמור את עמודת החיזוי. כדי לחזור לקנה המידה המקורי, השתמש בעמודת נוסחה חדשה > לוגיסטיקה > מיוחדות.
- גרף את הריצות על מגרש טרינרי. צבעו את הנקודות בהתאם לתגובות (או לתגובות שהשתנו אם הוחל שינוי צורה): פתחו את Graph > Ternary Plot. בחר רק את גורמי התערובת עבור X, התוויית. לחץ לחיצה ימנית על כל אחד מהגרפים שהתקבלו, בחר מקרא שורה ולאחר מכן בחר בעמודת התגובה (שעברה המרה).
הערה: צביעת הנקודות על פי תגובות נותנת פרספקטיבה חזותית בלתי תלויה במודל של התנהגות ביחס לגורמי תערובת. - מחק את סקריפט המודל שנוצר על-ידי Space-Filling Design.
- בנה מודל עצמאי עבור כל תגובה כפונקציה של גורמי המחקר, תוך חזרה על השלבים הבאים עבור כל תגובה.
הערה: במקרה של תגובה בינארית משנית (למשל, כשל ניסוח או מוות של עכבר), מודל גם תגובה זו. שנה את הגדרת התפלגות היעד מ- Normal ל - Binomial. - בניית מודל "מלא" הכולל את כל השפעות המועמד. מודל זה צריך לכלול את ההשפעות העיקריות של כל גורם, אינטראקציות דו-כיווניות ותלת-כיווניות, מונחים מעוקבים ריבועיים וחלקיים חלקיים בגורמי התהליך, ומונחים מעוקבים של Scheffé עבור גורמי התערובת23,24.
הערה: השתמש באותה קבוצה של אפקטים של מועמדים עבור כל תגובה. טכניקת בחירת מודל SVEM תחדד באופן עצמאי את המודלים עבור כל תגובה, מה שעשוי להוביל למודלים מופחתים ייחודיים עבור כל תגובה. איור 9 ממחיש חלק מההשפעות המועמדות האלה. שלבי המשנה הבאים מפרטים תהליך זה.- בחר Analyze > Fit Model.
- ודא שגורמים חוסמים (למשל, יום) אינם מורשים לקיים אינטראקציה עם גורמי מחקר אחרים. בחר גורמים חוסמים ולחץ על הוסף. אל תכלול גורמים אלה באף אחד משלבי המשנה הבאים.
הערה: חשוב לקחת בחשבון גורמים חוסמים במודל, אך אין לאפשר לגורמים חוסמים לקיים אינטראקציה עם גורמי מחקר אחרים. המטרה העיקרית של גורמים חוסמים היא לסייע בשליטה על השתנות הניסוי ולשפר את רגישות הניסוי. - הדגישו את כל גורמי המחקר. שנה את ערך השדה Degree ל- 3 (הוא מוגדר ל- 2 כברירת מחדל). לחץ על Factorial לתואר.
הערה: פעולה זו כוללת אפקטים עיקריים וכן אינטראקציות דו-כיווניות ותלת-כיווניות במודל. - בחרו רק בגורמים שאינם תערובת בחלון הבחירה. לחץ על פקודות מאקרו > קוביות חלקיות.
הערה: פעולה זו מציגה אפקטים ריבועיים עבור גורמי התהליך הרציף והאינטראקציה שלהם עם גורמים אחרים שאינם תערובת במודל. - בחרו רק את גורמי התערובת מרשימת הבחירה. לחץ על פקודות מאקרו > Scheffe Cubic. בטל את ההפעלה של אפשרות ברירת המחדל ללא יירוט (עיין באיור 9).
הערה: הכללת יירוט במודל היא שלב חיוני בעת שימוש בשיטות לאסו והיא מועילה גם בהקשר הבחירה קדימה. הגדרת ברירת המחדל המסורתית No Intercept קיימת בדרך כלל מכיוון שהתאמת יירוט בו זמנית עם כל ההשפעות העיקריות של התערובת, ללא שינויים כגון גישת SVEM, אינה אפשרית עם הליך רגרסיה רגיל של ריבועים לפחות12. - ציין את עמודת התגובה: סמן את עמודת התגובה ולחץ על Y.
- שנה את הגדרת האישיות לרגרסיה כללית. השאר את האפשרות 'תפוצה רגילה'.
- שמור הגדרת מודל זו בטבלת הנתונים לשימוש עם תגובות נוספות על-ידי לחיצה על תפריט המשולש האדום לצד מפרט דגם ובחירה באפשרות שמור בטבלת הנתונים.
- החל את שיטת הבחירה קדימה של SVEM כך שתתאים למודל המופחת, ללא הכללה הכרחית של ההשפעות העיקריות של גורם התערובת, ואחסן את עמודת נוסחת החיזוי בטבלת הנתונים.
- בתיבת הדו-שיח התאמת מודל , לחץ על הפעל.
- לשיטת האומדן, בחר SVEM Forward Selection.
- הרחיבו את התפריטים Advanced Controls > Force Terms ובטלו את הבחירה בתיבות המשויכות לאפקטים העיקריים של התערובת. רק התיבה מונח יירוט צריכה להישאר מסומנת. איור 10 מציג את הגדרת ברירת המחדל שבה מאולצים האפקטים העיקריים. עבור שלב זה, יש לבטל סימון של תיבות אלה כדי לאפשר למודל לכלול או לא לכלול השפעות אלה בהתבסס על הליך הבחירה קדימה.
- לחץ על Go כדי להפעיל את הליך SVEM Forward Selection.
- התווה את התגובות בפועל לפי התגובות החזויות ממודל SVEM כדי לאמת יכולת ניבוי סבירה. (איור 11). לחץ על המשולש האדום לצד SVEM Forward Selection ובחר Diagnostic Plots > Plot Actual by Predicted.
- לחץ על המשולש האדום לצד SVEM Forward Selection ובחר Save Columns > Save Prediction Formula כדי ליצור עמודה חדשה המכילה את נוסחת החיזוי בטבלת הנתונים.
- אופציונלי: חזור על השלבים לעיל באמצעות SVEM Lasso כשיטת הערכה כדי לקבוע אם מוצע מתכון אופטימלי אחר לאחר ביצוע השלבים הבאים. אם כן, הפעל את שני המתכונים כריצות אישור (נדון בסעיף 5) כדי לראות איזה מהם משיג את הביצועים הטובים ביותר בפועל12.
- חזור על שלבי בניית המודל עבור כל תגובה.
- לאחר שמירת עמודות החיזוי של כל התגובות בטבלת הנתונים, צור גרף של עוקבי התגובה עבור כל עמודות התגובה החזויות באמצעות פלטפורמת Profiler: בחר Graph > Profiler, ובחר את כל עמודות החיזוי שנוצרו בשלב הקודם עבור Y, Prediction Formula, ולחץ על OK (איור 12).
- זהה את הניסוח האופטימלי של המועמד.
- הגדר את "פונקציית הרצון" עבור כל תגובה, וציין אם יש למקסם את התגובה, למזער אותה או להתאים אותה למטרה. הגדר כל תגובה ראשית לשימוש במשקל חשיבות של 1.0 וכל תגובה משנית לשימוש במשקל חשיבות של 0.2. מתפריט המשולש האדום Prediction Profiler, בחר Optimization and Desirability > Desirability Functions, ולאחר מכן Optimization and Desirability > Set Desirabilities. הזן את ההגדרות בחלונות הבאים.
הערה: המשקלים החשובים הם יחסיים וסובייקטיביים, ולכן כדאי לבדוק את רגישות האופטימום המשולב לשינויים במשקלים אלה בטווח סביר (למשל, משקלול שווה לשקלול 1:5). - פקדו על יוצר הפרופילים למצוא את הגדרות הגורמים האופטימליות שממקסמות את פונקציית הרצויות (איור 12): מתוך הפרופילר, בחרו Optimization and Desirability > Maximize Desirability.
הערה: הערכים החזויים של התשובות אצל המועמדים האופטימליים עשויים להעריך יתר על המידה את הערך של תגובות מוטות ימינה כגון עוצמה; עם זאת, ריצות האישור יספקו תצפיות מדויקות יותר על ניסוחים מועמדים אלה. המטרה העיקרית היא לאתר את הניסוח האופטימלי ( ההגדרות של המתכון האופטימלי). - רשום את הגדרות הגורמים האופטימליות ושים לב לשקלולים החשובים המשמשים לכל תגובה: בתפריט Prediction Profiler , בחר הגדרות גורם > זכור הגדרות.
- הגדר את "פונקציית הרצון" עבור כל תגובה, וציין אם יש למקסם את התגובה, למזער אותה או להתאים אותה למטרה. הגדר כל תגובה ראשית לשימוש במשקל חשיבות של 1.0 וכל תגובה משנית לשימוש במשקל חשיבות של 0.2. מתפריט המשולש האדום Prediction Profiler, בחר Optimization and Desirability > Desirability Functions, ולאחר מכן Optimization and Desirability > Set Desirabilities. הזן את ההגדרות בחלונות הבאים.
- אופציונלי: עבור גורמים קטגוריים כגון סוג שומנים מיוננים, מצא את הנוסחאות האופטימליות המותנות עבור כל רמת גורם.
- תחילה הגדר את הרמה הרצויה של הגורם בפרופיל, לאחר מכן החזק את מקש Ctrl ולחץ לחיצה שמאלית בתוך הגרף של גורם זה ובחר הגדרת גורמי נעילה. בחר מיטוב ורצון > למקסם את הרצינות כדי למצוא את האופטימלי המותנה כאשר גורם זה נעול בהגדרה הנוכחית שלו.
- בטל את נעילת הגדרות הגורם לפני שתמשיך, באמצעות אותו תפריט המשמש לנעילת הגדרות הגורמים.
- חזור על תהליך המיטוב לאחר התאמת משקלי החשיבות של התגובות (באמצעות אופטימיזציה ורצון> הגדרת רצון), אולי רק אופטימיזציה של התגובות הראשוניות או הגדרת חלק מהתגובות המשניות כבעלות משקל חשיבות פחות או יותר, או הגדרת המטרה של התגובות המשניות ללא (איור 13).
- הקלט את המועמד האופטימלי החדש (בתפריט Prediction Profiler , בחר הגדרות גורם > זכור הגדרות.)
- הפקת סיכומים גרפיים של האזורים האופטימליים של מרחב הגורמים: יצירת טבלת נתונים עם 50,000 שורות המאוכלסות בהגדרות גורמים שנוצרו באופן אקראי בתוך מרחב הגורמים המותר, יחד עם הערכים החזויים המתאימים מהמודל המופחת עבור כל אחת מהתגובות ופונקציית הרצון המשותף.
- ב- Profiler, בחר Output Random Table. הגדר כמה ריצות להדמיה? ל- 50,000 ולחץ על אישור .
הערה: פעולה זו יוצרת טבלה חדשה עם הערכים החזויים של התגובות בכל אחד מ- 50,000 הניסוחים. העמודה Desirability תלויה במשקלי החשיבות של התגובות הקיימות כשבוחרים באפשרות Output Random Table . - בטבלה החדשה שנוצרה, הוסף עמודה חדשה המחשבת את האחוזון של העמודה רצוי. השתמש בעמודת אחוזון זו בתרשימים הטרינריים במקום בעמודת הרצויות הגולמית. לחץ באמצעות לחצן העכבר הימני על כותרת העמודה Desirability ובחר New Formula Column > Distributional > Cumulative Probability כדי ליצור עמודה חדשה של הסתברות מצטברת[Desirability].
- צור את הגרפיקה המתוארת בשלבים הבאים. שנה שוב ושוב את ערכת הצבעים של הגרפיקה כדי להציג את התחזיות עבור כל תגובה ועבור העמודה הסתברות מצטברת[רצון].
- בניית חלקות טרינריות עבור ארבעת גורמי השומנים. בטבלה, נווט אל Graph > Ternary Plot, בחר בגורמי התערובת עבור X, Plotting ולחץ על OK. לחץ לחיצה ימנית באחד התרשימים שנוצרו, בחר מקרא שורה ולאחר מכן בחר בעמודת התגובה החזויה. שנה את התפריט הנפתח צבעים ל- Jet.
הערה: פעולה זו מציגה את האזורים בעלי הביצועים הטובים ביותר והגרועים ביותר ביחס לגורמי השומנים. איור 14 מציג את אחוזוני הרצון של המפרק כאשר שוקלים למקסם עוצמה (חשיבות=1) ולמזער את הגודל (חשיבות=0.2), תוך ממוצע על פני כל הגורמים שאינם מוצגים על צירי העלילה הטרינריים. איור 15 מציג את הגודל הגולמי החזוי. סביר גם לפרק גרפים אלה באופן מותנה בגורמים אחרים, כגון יצירת קבוצה מובחנת של תרשימים טרינריים לכל סוג ליפיד מיונן עם מסנן נתונים מקומי (זמין מתפריט המשולש האדום ליד Ternary Plot). - באופן דומה, השתמש ב - Graph > Graph Builder כדי להתוות את 50,000 הנקודות המקודדות בצבע (המייצגות ניסוחים ייחודיים) כנגד גורמי התהליך שאינם מעורבים, בנפרד או במשותף, וחפש קשרים בין התגובות והגורמים. חפש את הגדרות הגורמים המניבות את הכדאיות הגבוהה ביותר. גלה שילובים שונים של גורמים בגרפיקה.
הערה: בשעת צביעת תרשימים, השתמש בהסתברות מצטברת [Desirability], אך בעת התוויית הרצויות על הציר האנכי כנגד גורמי תהליך השתמש בעמודה Raw Desirability . ניתן גם למקם את עמודת הרצויות על ציר של ההדמיה התלת-ממדית Graph > Scatterplot יחד עם שני גורמי תהליך אחרים לחקר רב-משתנים. איור 16 מראה את הכדאיות המשותפת של כל הפורמולציות שיכולות להיווצר עם כל אחד משלושת סוגי השומנים המיוננים. הפורמולציות הרצויות ביותר משתמשות ב-H102, כאשר H101 מספק כמה חלופות תחרותיות פוטנציאליות. - שמור את Profiler ואת ההגדרות הזכורות שלו בחזרה לטבלת הנתונים. לחץ על המשולש האדום לצד Profiler ובחר שמור סקריפט > לטבלת הנתונים....
- ב- Profiler, בחר Output Random Table. הגדר כמה ריצות להדמיה? ל- 50,000 ולחץ על אישור .
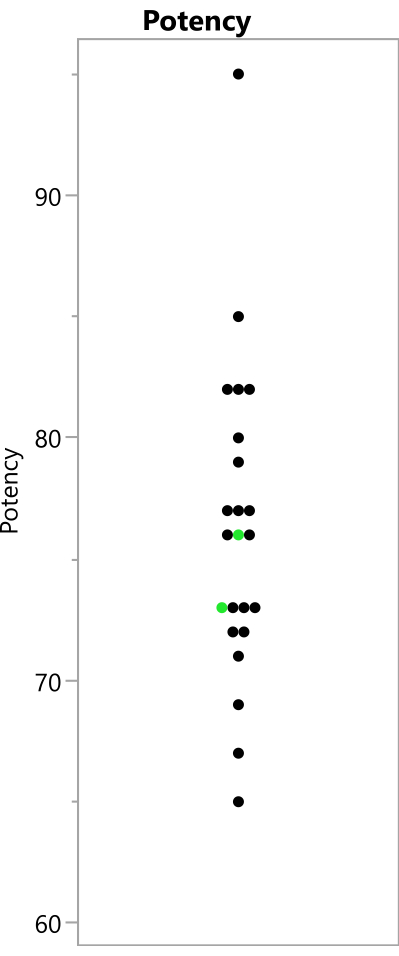
איור 8: נצפו קריאות עוצמה מהניסוי. הנקודות מציגות את ערכי העוצמה שנצפו מ-23 הריצות; ריצות השוואת הביצועים המשוכפלות מוצגות בירוק. אנא לחץ כאן כדי להציג גרסה גדולה יותר של איור זה.

איור 9: דו-שיח תוכנה להתחלת הניתוח. ההשפעות המועמדות הוזנו יחד עם תגובת עוצמת המטרה, והאפשרות No Intercept לא נבדקה. אנא לחץ כאן כדי להציג גרסה גדולה יותר של איור זה.
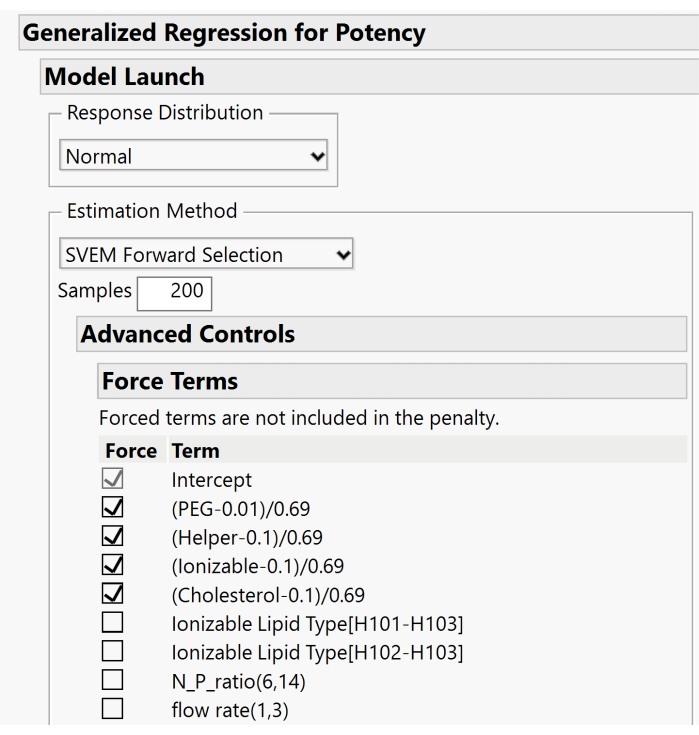
איור 10. תיבת דו-שיח נוספת לציון אפשרויות SVEM. כברירת מחדל, ההשפעות העיקריות של השומנים נאלצות לתוך המודל. מכיוון שכלול יירוט, אנו ממליצים לבטל את הסימון של תיבות אלה כדי לא לכפות את האפקטים. אנא לחץ כאן כדי להציג גרסה גדולה יותר של איור זה.
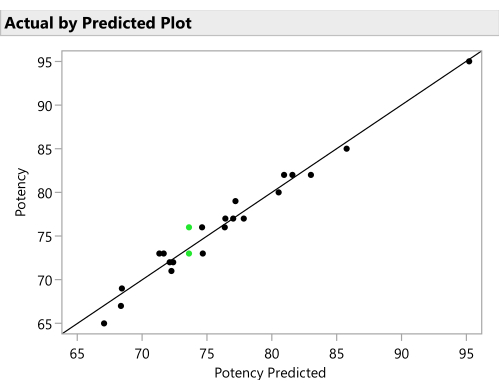
איור 11: בפועל לפי העלילה החזויה. איור זה משרטט את העוצמה הנצפית כנגד הערך שנחזה עבור כל ניסוח על-ידי מודל SVEM. המתאם לא צריך להיות חזק כמו בדוגמה הזאת, אבל הציפייה היא לראות לפחות מתאם מתון ולבדוק חריגים. אנא לחץ כאן כדי להציג גרסה גדולה יותר של איור זה.

איור 12: פרופיל חיזוי. שתי שורות הגרפים העליונות מציגות את פרוסות פונקציית התגובה החזויה בניסוח האופטימלי (כפי שזוהה בגישת SVEM). השורה התחתונה של הגרפים מציגה את ה"רצון" המשוקלל של הניסוח, שהוא פונקציה של העמודה האחרונה של הגרפים שמראה שיש למקסם את העוצמה, ולמזער את הגודל. אנא לחץ כאן כדי להציג גרסה גדולה יותר של איור זה.

איור 13: שלושה מועמדים אופטימליים לניסוח מתוך SVEM-Forward Selection. שינוי שקלול החשיבות היחסית של התגובות יכול להוביל לניסוחים אופטימליים שונים. אנא לחץ כאן כדי להציג גרסה גדולה יותר של איור זה.
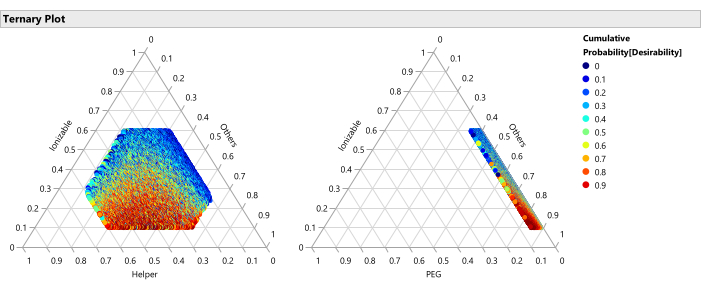
תרשים 14: חלקות טרינריות לאחוזון הכדאיות. העלילה מציגה את 50,000 הפורמולציות המקודדות בצבע לפי אחוזון רצון, כאשר הרצון נקבע עם משקל חשיבות של 1.0 למקסום העוצמה ו-0.2 למזעור הגודל, חלקות אלה מראות כי האזור האופטימלי של הפורמולציות מורכב מאחוזים נמוכים יותר של שומנים מיוננים ואחוזים גבוהים יותר של PEG. אנא לחץ כאן כדי להציג גרסה גדולה יותר של איור זה.

איור 15: תרשים טרינרי עבור הגודל החזוי. העלילה מציגה את תחזיות הגודל ממודל SVEM עבור כל אחד מ-50,000 הפורמולציות. הגודל ממוזער עם אחוזים גבוהים יותר של שומנים עוזרים ומוגדל עם אחוזים נמוכים יותר של עוזר. מכיוון שהגורמים האחרים משתנים באופן חופשי בין 50,000 הניסוחים המשורטטים, משמעות הדבר היא שקשר זה מתקיים על פני הטווחים של הגורמים האחרים (PEG, קצב זרימה וכו '). אנא לחץ כאן כדי להציג גרסה גדולה יותר של איור זה.

איור 16: שרטוטי כינור לכדאיות של ניסוחים הכוללים את שלושת סוגי השומנים המייננים השונים. כל אחת מ-50,000 הנקודות מייצגת ניסוח ייחודי מכל מרחב הגורמים המותר. השיאים של התפלגויות אלה הם הערכים המקסימליים של הרצויות המחושבים באופן אנליטי עם פרופיל החיזוי. H102 הוא בעל הפסגה הגדולה ביותר ולכן מייצר את הנוסחה האופטימלית. גישת SVEM לבניית המודל שמייצר פלט זה מסננת באופן אוטומטי גורמים חסרי משמעות סטטיסטית: מטרת גרף זה היא לשקול מובהקות מעשית בכל רמות הגורמים. אנא לחץ כאן כדי להציג גרסה גדולה יותר של איור זה.
5. ריצות אישור
- הכינו טבלה המפרטת את המועמדים האופטימליים שזוהו בעבר (איור 17).
הערה: הערכים True Potency ו-True Size באיור 17 ממולאים באמצעות פונקציות היצירה המדומות (סימולציה): בפועל, הערכים האלה יתקבלו על-ידי ניסוח ולאחר מכן מדידה של הביצועים של המתכונים האלה.- כלול את בקרת אמת המידה עם קבוצת ריצות המועמדים שתגובש ותמדוד.
- אם אחד מהניסוחים מהניסוי נמצא כמניב תוצאות רצויות, אולי על ידי ביצועים טובים יותר מאמת המידה, בחר את הטוב ביותר להוסיף לטבלת המועמדים ובדוק שוב יחד עם ניסוחים חדשים.
הערה: הוסף ידנית ריצות רצויות לטבלת המועמדים או השתמש בהגדרות נזכרות בחלון Profiler אם ריצות אלה הן מהניסוי הקודם. זהה את מספר השורה של הריצה, נווט אל Prediction Profiler > הגדרות גורם > הגדר לנתונים בשורה והזן את מספר השורה. לאחר מכן, בחר Prediction Profiler > Factor Settings > Remember Settings ותייג בהתאם (לדוגמה, "benchmark" או "best run from the previous experiment"). - לחץ לחיצה ימנית על הטבלה Remembered Settings ב- Profiler ובחר הפוך לטבלת נתונים.
הערה: בהתאם לעדיפות ולתקציב של המחקר, שקול להפעיל עותקים משוכפלים עבור כל ריצת אישור, במיוחד אם אתה מחליף את אמת המידה. צור ונתח כל ניסוח פעמיים, תוך שימוש בתוצאה הממוצעת לדירוג. שימו לב לכל מועמד עם טווח תגובה רחב על פני שני העותקים המשוכפלים, שכן זה יכול להצביע על שונות גבוהה בתהליכים. - במידת הצורך עקב אילוצי תקציב, בחר מטה מבין המועמדים שזוהו כדי להתאים לתקציב הניסוי או כדי לחסל מועמדים מיותרים.
- בצע את ריצות האישור. בנו את הניסוחים ואספו את הקריאות.
- בדוק את העקביות בין התוצאות מהניסוי המקורי לבין התוצאות עבור אצוות האישור עבור אמות מידה או מתכונים חוזרים אחרים. אם יש שינוי גדול ובלתי צפוי, אז לשקול מה יכול היה לתרום למשמרת ואם זה אפשרי כי כל ריצות של אצוות אישור הושפעו.
- השווה את הביצועים של ניסוחים אופטימליים של המועמד. בדוק אם מועמדים חדשים השיגו ביצועים טובים יותר מאמת המידה.
- אופציונלי: הוסף את התוצאה של ריצות האישור לטבלת הניסויים והפעל מחדש את הניתוח בסעיף 4.
הערה: השלב הבא של זרימת העבודה מספק הוראות לבניית מחקר המשך טיפול יחד עם הפעלות אלה, במידת הצורך.

תרשים 17: טבלה של עשרה מועמדים מיטביים לריצה כמועמד לאישור. העוצמה האמיתית והגודל האמיתי מולאו מפונקציות יצירת הסימולציה (ללא כל תהליך נוסף או וריאציה אנליטית). אנא לחץ כאן כדי להציג גרסה גדולה יותר של איור זה.
6. אופציונלי: תכנון מחקר המשך שירוץ במקביל לריצות האישור
- להעריך את הצורך במחקר מעקב בהתחשב בקריטריונים הבאים:
- קבע אם הניסוח האופטימלי נמצא לאורך אחד מגבולות הגורמים ואם רוצים ניסוי שני להרחיב לפחות אחד מטווחי הגורמים.
- להעריך אם הניסוי הראשוני השתמש בגודל ריצה קטן יחסית או בטווחי גורמים גדולים יחסית ואם יש צורך "להתקרב לאזור" שזוהה עם ריצות נוספות וניתוח מעודכן.
- בדוק אם גורם נוסף מוצג. זה יכול להיות רמה של גורם קטגורי כגון שומנים מיוננים נוספים או גורם שנשאר קבוע במחקר הראשוני, למשל, ריכוז חיץ.
- אם אף אחד מהתנאים לעיל אינו מתקיים, המשך לשלב 7.
- התכוננו לריצות ניסיוניות נוספות שיבוצעו במקביל לריצות האישור.
- הגדר את גבולות הגורמים המבטיחים חפיפה חלקית עם האזור מהמחקר הראשוני. אם אין חפיפה, יש לתכנן מחקר חדש.
- פתח את ריצות הניסוי החדשות עם עיצוב ממלא מקום. בחר DOE > Special Purpose > Space Filling Design.
הערה: עבור משתמשים מתקדמים, שקול עיצוב D-optimal באמצעות DOE > Custom Design. - לאחר יצירת ריצות מילוי החלל, שלבו ידנית שתיים או שלוש ריצות מהניסוי המקורי שנמצאות בתוך מרחב הגורם החדש. חלק הפעלות אלה באופן אקראי בתוך טבלת הניסוי באמצעות השלבים המתוארים בסעיף 2 כדי להוסיף שורות ולאחר מכן סדר שורות באופן אקראי.
הערה: אלה ישמשו להערכת כל תזוזה באמצעי התגובה בין בלוקים. - שרשור ריצות האישור ומילוי החלל החדש יופעל בטבלה אחת וסדר את סדר ההפעלה באופן אקראי. השתמש בטבלאות > שרשור ולאחר מכן צור ומיין לפי עמודה אקראית חדשה כדי להפוך את סדר ההפעלה לאקראי, כמתואר בסעיף 2.
- נסחו את המתכונים החדשים ואספו את התוצאות.
- שרשר את ריצות הניסוי והתוצאות החדשות לטבלת נתוני הניסוי המקורית, והוסף עמודת מזהה ניסוי כדי לציין את המקור של כל תוצאה. השתמש בטבלאות > 'שרשור ' ובחר באפשרות 'צור עמודת מקור'.
- ודא שמאפייני העמודה של כל גורם מציגים את הטווח המשולב בשני המחקרים: לחץ לחיצה ימנית על כותרת העמודה עבור כל גורם ובדוק את טווחי המאפיינים Coding ו - Blend , אם קיימים.
- התחל לנתח את תוצאות הניסוי החדש.
- כלול את עמודת מזהה הניסוי כמונח במודל כדי לשמש גורם חוסם. ודא שמונח זה אינו מקיים אינטראקציה עם גורמי המחקר. הפעל את סקריפט הדו-שיח Fit Model שנשמר בטבלה במקטע 4, בחר בעמודת מזהה הניסוי ולחץ על Add כדי לכלול אותה ברשימת האפקטים המועמדים.
- הפעל תיבת דו-שיח זו של מודל התאמה בטבלת הנתונים המשורשרת כדי לנתח במשותף את התוצאות מהניסוי החדש ומהמחקר הראשוני. היצמד להוראות קודמות כדי ליצור מועמדים מעודכנים לניסוח אופטימלי וסיכומים גרפיים.
- לצורך תיקוף, יש לנתח באופן עצמאי את תוצאות הניסוי החדש, למעט תוצאות הניסוי הראשוני. כלומר, לבצע את השלבים המתוארים בסעיף 4 בטבלת הניסויים החדשה.
- ודא כי ניסוחים אופטימליים שזוהו על ידי מודלים אלה תואמים באופן הדוק עם אלה המוכרים על ידי הניתוח המשותף.
- סקור סיכומים גרפיים כדי לאשר שגם הניתוח המשותף וגם הניתוח האישי של תוצאות הניסוי החדש מציגים התנהגויות שטח תגובה דומות (כלומר, קיים קשר דומה בין התגובות(ות) לבין הגורמים).
- השווה את הניתוחים המשולבים והאינדיבידואליים של תוצאות חדשות עם הניסוי הראשוני לקבלת עקביות. השתמש במבני גרפים דומים להשוואה ובחן את המתכונים האופטימליים שזוהו להבדלים.
7. תיעוד המסקנות המדעיות הסופיות של המחקר
- אם פקד השוואת הביצועים ישתנה למתכון חדש שזוהה עקב המחקר, רשום את ההגדרה החדשה וציין את קבצי העיצוב והניתוח המתעדים את מקורו.
- שמור את כל טבלאות הניסוי וסיכומי הניתוח, רצוי עם שמות קבצים עם חותמת תאריך, לעיון עתידי.
תוצאות
גישה זו אומתה בשני סוגי השומנים המסווגים באופן רחב: ליפידים קלאסיים דמויי MC3 וליפידואידים (למשל, C12-200), הנגזרים בדרך כלל מכימיה קומבינטורית. בהשוואה לנוסחת LNP שפותחה בשיטת One Factor at a Time (OFAT), הניסוחים המועמדים שנוצרו באמצעות זרימת העבודה שלנו הדגימו לעתים קרובות שיפורי עוצמה של פי 4 עד פי 5 בסולם לוגריתמי, כפי שמוצג בקריאות לוציפראז של כבד העכבר באיור 18. טבלה 1 מתארת את השיפורים המתאימים בביטוי לוציפראז בכבד עכבר שנצפו במהלך ביצועי בקרת אמת המידה לאורך שני שלבי אופטימיזציה (מחקר ראשוני ומחקר מעקב לאחר מכן). בשלב הראשון, ההתמקדות הייתה באופטימיזציה של יחסי השומנים תוך שמירה על גורמים אחרים קבועים. במחקר המעקב הוצג סוג שומנים עוזר נוסף ובוצעה אופטימיזציה בהתחשב הן בהרכב יחס השומנים והן בסוג השומנים המסייעים. כתוצאה מכך, סוג השומנים המסייע החדש שהוצג נבחר לשימוש עם הרכב השומנים הממוטב המשויך. השיפור המשמעותי בעוצמה מצביע על כך שהרכבים אופטימליים אלה עשויים להציג יכולות בריחה אנדוזומליות טובות יותר25.
ניתן להשתמש בסימולציות כדי להראות את האיכות הצפויה של המועמד האופטימלי המיוצר על ידי הליך זה. במסגרת הניסוי לדוגמה המשמש בפרוטוקול, אנו יכולים לחזור על הסימולציה פעמים רבות עבור גדלי ריצה שונים ולהעריך את התוצאות בהתאם לפונקציה מחוללת התהליך המדומה. סקריפט JMP למטרה זו מסופק בקובץ משלים 4. באופן ספציפי, נוצר תכנון מילוי חלל ועמודות התגובה אוכלסו בערכים מפונקציות הגנרטור שלנו, בתוספת רעש המייצג שינויים אנליטיים ותהליכיים. אנו מתאימים את התגובות המדומות הללו לטכניקות ניתוח שונות (כולל SVEM Forward Selection) כדי לייצר מתכון אופטימלי מתאים למועמד. לאחר מכן משווים את המועמדים מכל שיטת ניתוח לערך של האופטימום האמיתי מהפונקציות היוצרות. איור 19 ממחיש את האחוז הממוצע של התגובה התיאורטית המקסימלית שהושגה על ידי כל אחת משלוש שיטות הניתוח באמצעות עיצובי מילוי חלל בגודל שניתן על הציר האופקי. המודל המלא, הכולל את כל ההשפעות המועמדות ואינו מצמצם את המודל על סמך המובהקות הסטטיסטית של השפעות אלה, מבצע את הגרוע ביותר. חלק ניכר מהעבודה הנוספת המושקעת באופן מסורתי בהתאמת מודלים של רגרסיה לניסויי תערובת-תהליך כרוכה בשינויים (הסרת היירוט, אילוץ ההשפעות העיקריות של התערובת, מניעת שימוש באפקטים של תערובת ריבועית טהורה וכו') הנדרשים כדי להתאים למודל9 המלא הזה, ומנקודת מבט זו, הליכים אלה מיותרים12. יתר על כן, מודל זה אינו יכול להתאים עד שגודל העיצוב מגיע למספר האפקטים במודל. בגדלים ניסיוניים קטנים יותר, אנו יכולים להתאים את שיטת הבחירה קדימה המסורתית, אשר עולה על הביצועים של המודל המלא ביחס לביצועים הממוצעים של ניסוח המועמד האופטימלי עבור כל גודל ניסוי קבוע. כמו כן, שינוי SVEM לגישת בחירה קדימה זו משפר עוד יותר את הביצועים של המועמדים האופטימליים. תרשים זה מגלה כי שימוש ב- SVEM-Forward Selection12,13 לניתוח ניסוי מילוי חלל בן 24 ריצות משיג את אותה איכות ממוצעת, הדורשת בדרך כלל 50 ריצות כאשר מנתחים אותה באמצעות מודל בחירה קדימה מסורתי (מיקוד AICc מינימלי). למרות שהביצועים בפועל ישתנו מתהליך לתהליך, סימולציה זו - יחד עם התוצאות שפורסמו על SVEM 12,13,16,17,26 - מדגימות את הפוטנציאל של הליך מידול זה לאופטימיזציה של פורמולציה.
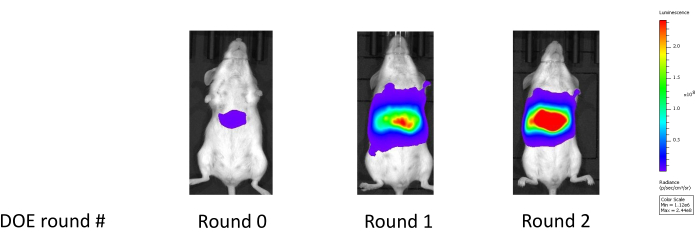
איור 18: שיפור בביטוי לוציפראז בכבד לאחר שני סבבי ניסויים. סיבוב 0 מראה את קריאת לוציפראז הכבד עבור ניסוח אמת המידה; סבב 1 מראה את קריאת הלוציפראז בכבד לאחר הניסוי הראשון אשר מייעל את היחסים המולריים של השומנים המרכיבים את LNP; סבב 2 מראה את קריאת לוציפראז בכבד לאחר הניסוי השני, אשר מייעל עוד יותר את היחסים המולריים המרכיבים תוך התחשבות בסוג שומנים עוזר נוסף. אנא לחץ כאן כדי להציג גרסה גדולה יותר של איור זה.
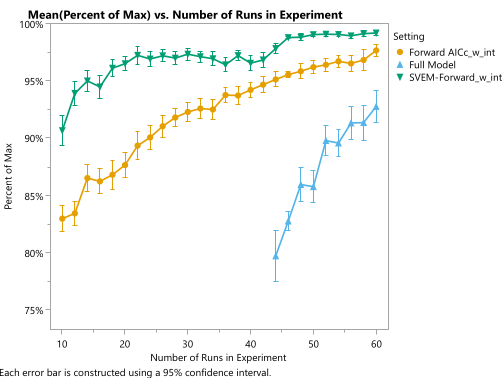
תרשים 19: איכות הניסוח האופטימלי כפונקציה של גודל הניסוי והמודל הסטטיסטי. הציר האנכי מייצג את אחוז הרצון המרבי התיאורטי, והציר האופקי מייצג את גודל העיצוב הממלא את החלל. כל נקודה מציגה ממוצע של מעל 150 סימולציות. הקו הכחול (משולשים) מייצג את המודל המלא (ללא ביטול השפעות חסרות משמעות סטטיסטית), קו הענבר (עיגולים) מייצג את מודל הבחירה קדימה המסורתי מבוסס AICc (עם יירוט ומבלי לכפות אפקטים עיקריים של התערובת), והקו הירוק (משולשים הפוכים) מייצג את מודל הבחירה קדימה מבוסס SVEM (עם יירוט ומבלי לכפות אפקטים עיקריים של תערובת). אנא לחץ כאן כדי להציג גרסה גדולה יותר של איור זה.
| סיבוב | מזהה חלקיק | ביטוי לוציפראז בכבד (פוטון/שנייה) |
| 0 | מדד בקרה | 8.ה+06 |
| 1 | ממוטב מעל יחסי שומנים | 2.ה+09 |
| 2 | ממוטב מעל יחס שומנים וסוג שומנים עוזר | 8.ה+10 |
טבלה 1: שיפור שיטתי בביטוי לוציפראז באמצעות אופטימיזציה של תכנון ניסוי (DOE). טבלה זו ממחישה את השיפור המשמעותי בביטוי של לוציפראז, עם שיפור של עד פי 10,000 בסולם הפוטון/שנייה, מאמת המידה הראשונית ועד ל"מועמד האופטימלי" הסופי.
קובץ משלים 1: 04APR2023 סיכום.docx - מסמך זה מספק תיעוד של המחקר כולל מטרתו, התגובות שהוערכו, הגורמים שנלקחו בחשבון והמספר הכולל של הריצות שבוצעו. אנא לחץ כאן כדי להוריד קובץ זה.
קובץ משלים 2: 23_run_simulated_experiment.jmp - קובץ JMP עם הניסוי המדומה ותוצאותיו. קובץ זה כולל גם סקריפטים מצורפים לניתוח התואמים ל- JMP 17 Pro. אנא לחץ כאן להורדת קובץ זה.
קובץ משלים 3: 23_run_simulated_experiment.xlsx - קובץ אקסל הכולל את הניסוי המדומה ותוצאותיו, מתאים לקוראים שאין להם גישה ל-JMP. אנא לחץ כאן כדי להוריד קובץ זה.
קובץ משלים 4: סימולציית תערובת 20DEC22.jsl - זהו סקריפט JMP 17 Pro המשמש להדמיית ניסויי ניסוח LNP והערכת הביצועים של שיטות ניתוח שונות. קובץ ה- Script משתמש בגישת SVEM-Forward Selection (ללא יירוט), שהיא שיטת ניתוח המפתח המשמשת בזרימת עבודה זו. אנא לחץ כאן כדי להוריד קובץ זה.
Discussion
תוכנה מודרנית לתכנון וניתוח של ניסויי תהליך תערובות מאפשרת למדענים לשפר את נוסחאות ננו-חלקיקי השומנים שלהם בתהליך עבודה מובנה המונע ניסויי OFAT לא יעילים. גישת מידול SVEM שפותחה לאחרונה מבטלת רבים משינויי הרגרסיה הארכאיים ואסטרטגיות הפחתת המודלים שאולי הסיחו בעבר את דעתם של מדענים עם שיקולים סטטיסטיים זרים. לאחר איסוף התוצאות, מסגרת ניתוח SVEM מציעה גישה שהיא גם קלה יותר ליישום וגם נוטה לייצר מודלים טובים יותר מאשר גישות מידול מסורתיות13. יתר על כן, הניתוחים הגרפיים המבוססים על נוסחאות החיזוי עבור כל תגובה ניתנים לפירוש בקלות על ידי מדענים, ונותנים סיכום ברור של ההתנהגות השולית של התגובה על פני גורמים בודדים, כמו גם קבוצות קטנות של גורמים מבלי לדרוש פרשנות של אומדני פרמטרים מתואמים מאוד ממודל רגרסיה. זה מאפשר למדענים להתמקד בהערכת מובהקות מעשית על פני גורמי מחקר לאחר ש- SVEM הסיר באופן אוטומטי השפעות חסרות משמעות סטטיסטית.
זרימת העבודה שימשה בפועל לשינוי שיטתי של הרכב השומנים ופרמטרי הניסוח כגון יחס N/P, קצב זרימה ויחס ערבוב לצורך אופטימיזציה ולבחירת סוגי השומנים המסייעים הטובים ביותר, סוגי שומנים מיוננים וסוגי חיץ. המטרות בדוגמאות אלה כוללות בדרך כלל מקסום העוצמה in vivo או in vitro ועטיפת מטענים משתנים כמו mRNA או DNA עבור מטרות in vivo רלוונטיות כגון תאי כבד, או לפעמים על פני סוגי תאים מרובים במקרה של יישומי in vitro. עבור יישומים ספציפיים, ייתכן שנצטרך לאזן תכונות ביופיזיקליות כגון גודל, PDI, פוטנציאל zeta ואחוז אנקפסולציה תוך בחינת עוצמת in vivo. בנוסף, המטרה היא למצוא נוסחה חזקה, אך נסבלת היטב, ולכן אנו יכולים לכלול תגובות כגון שינוי במשקל הגוף, תגובת ציטוקינים, או אליציטוטציה של אנזימי כבד כגון AST/ALT בניתוח. דפוסים התפתחו מניסויי LNP רבים. יש לציין כי שינויים ביחס המולרי של השומנים המיוננים וביחס N/P משפיעים באופן משמעותי על אנקפסולציית RNA. יתר על כן, נראה כי שינויים ביחס המולרי של PEG משפיעים על יציבות החלקיקים, כפי שמצוין על ידי השפעות על גודל ו- PDI. באופן כללי, עודף של PEG בליבת LNP נוטה להיות בעל השפעה מזיקה על העוצמה בעכברים.
שיפורי ביצועים בולטים במיוחד כאשר יותר מתגובה אחת ממוקדת: גם אם אמת המידה כבר מתפקדת היטב ביחס לתגובה הראשונית (למשל, עוצמה), אופטימיזציה של המפרקים בדרך כלל שומרת או משפרת את ההתנהגות ביחס לתגובה הראשונית ובו זמנית משפרת התנהגות ביחס לתגובות אחרות (מזעור PDI, גודל או ירידה במשקל הגוף). אנו מאמתים את האותנטיות של שיפורים אלה באמצעות ריצות אישור, שבהן אנו מכינים ומשווים ישירות את ניסוח אמת המידה (אולי עם שכפול) ואת ניסוחי המועמדים החדשים.
שלב העיצוב של זרימת עבודה זו כולל מספר שלבים קריטיים. ראשית, ודא כי הגורמים והטווחים שלהם מוזנים כראוי לפלטפורמת העיצוב הממלאת את החלל. שנית, השתמש בגרפיקה ובידע בנושא כדי לאשר את ההיתכנות של כל ניסוח שנוצר לפני תחילת הניסוי. לבסוף, בצע את הניסוי לפי הסדר האקראי שצוין בטבלת התכנון. היצמדות לרצף זה מסייעת למנוע משתנים משותפים בלתי מדודים - כגון סדר ייצור הפורמולציה או טמפרטורת הסביבה - מלבלבל את הגורמים הנחקרים. העיצובים הממלאים את החלל קלים יותר לבנייה - עם פחות פוטנציאל לטעויות משתמש מאשר עיצובים אופטימליים של תהליכי תערובת, הדורשים החלטות נוספות במהלך ההתקנה שעלולות לתסכל משתמשים חסרי ניסיון ולהרתיע אותם מלהשתמש בניסויים מתוכננים. אף על פי כן, לאחר עבודה על פרוטוקול זה, מדענים עשויים להפיק תועלת מקריאה נוספת על האופן שבו עיצובים אופטימליים יכולים להחליף עיצובים ממלאים חלל בפרוטוקול, כפי שמתואר בפרק 6 של Goos and Jones (2011)27. במיוחד עבור מחקרי המשך ש"מתקרבים" לאזור אופטימלי - שבו יש פחות חשש לכשלים לאורך גבולות התערובת - עיצובים D-אופטימליים יכולים להיות יעילים יותר מעיצובים הממלאים את החלל.
כמו כן, שלב הניתוח של זרימת עבודה זו כולל מספר שלבים קריטיים. ראשית, ודא שהמודל מציין קבוצה מתאימה של השפעות מועמדים, כולל אינטראקציות, ולא רק את ההשפעות העיקריות (מסדר ראשון) של הגורמים. שנית, השתמש ב- SVEM Forward Selection כמסגרת המידול. שלישית, בטל את אפשרות ברירת המחדל No Intercept והימנע מכפיית אפקטים עיקריים של תערובת. לבסוף, להגדיר כראוי את פונקציות הרצויות עבור התגובות לפני הפעלת אופטימיזציה. עבור משתמשים ללא גישה ל- SVEM, הגישה הטובה ביותר היא להשתמש בבחירה קדימה מסורתית (מיקוד AICc מינימלי) עבור בעיית הרגרסיה12. הפרוטוקול מציין כי ניתן גם להשתמש ב-SVEM Lasso: בממוצע, גישה זו נותנת תוצאות דומות ל-SVEM Forward Selection, אם כי עבור מערכי נתונים מסוימים שתי הגישות עשויות לייצר ניסוחים אופטימליים שונים במקצת שניתן להשוות לריצות אישור12. עם זאת, SVEM Lasso ייתן תוצאות מידול נחותות אם המשתמש עושה את הטעות הקלה של שוכח להשבית את ברירת המחדל No Intercept אפשרות12: מסיבה זו, השתמשנו SVEM Forward Selection כשיטת ברירת המחדל, מכיוון שהיא חזקה יותר לאפשרות זו.
המגבלה העיקרית של שיטה זו היא שיהיו מדי פעם מחקרים עם מורכבות גדולה יותר שייהנו מעזרתו של סטטיסטיקאי לתכנון וניתוח. מצבים בהם תקציב הריצה מוגבל מהרגיל (מתחת להיוריסטיקת המינימום), התגובות בינאריות, ישנם מספר רב של גורמים קטגוריים או רמות של גורם קטגורי יחיד, כאשר מטרת המחקר היא לשקול ביטול גורם תערובת אחד או יותר מהמתכון, או כאשר ישנם אילוצים נוספים על מרחב הגורמים ניתן לגשת אחרת על ידי סטטיסטיקאי, כגון על ידי שימוש אופטימלי או היברידי12,28 עיצובים או על ידי הוספת מבנה נוסף לעיצוב. באופן ספציפי, עיצוב היברידי יכול להיווצר על ידי יצירת עיצוב ממלא מקום עם רוב הריצות המתוקצבות ולאחר מכן "להגדיל" את העיצוב עם הריצות הנותרות (בדרך כלל 2-4) באמצעות קריטריון D-אופטימלי. גישה היברידית נוספת היא ליצור עיצוב ממלא חלל על פני גורמי התערובת (שומנים) ורציפים (תהליך), ולאחר מכן להוסיף גורמים קטגוריים כלשהם באמצעות הקצאה "אופטימלית" של רמות גורמים. עם זאת, גישת התכנון הפשוטה למילוי חלל שננקטה בפרוטוקול פותחה בשנים האחרונות בתהליך של הרצת עשרות ניסויי אופטימיזציה של נוסחאות LNP, ואנו מאמינים שהיא מציעה גישה חזקה שתעבוד בהצלחה ברוב המקרים תוך מתן ביטחון למדענים ביכולתם להשתמש בניסויים מתוכננים.
Disclosures
אסטרטגיית התכנון הניסיוני העומדת בבסיס תהליך עבודה זה יושמה בשתי בקשות פטנט שבהן אחד המחברים הוא ממציא. בנוסף, Adsurgo, LLC היא שותפה מוסמכת של JMP. עם זאת, הפיתוח והפרסום של מאמר זה נעשו ללא כל צורה של תמריץ כספי, עידוד או תמריצים אחרים מצד JMP.
Acknowledgements
אנו מודים לעורך ולשופטים האנונימיים על הצעות ששיפרו את המאמר.
Materials
| Name | Company | Catalog Number | Comments |
| JMP Pro 17.1 | JMP Statistical Discovery LLC |
References
- Dolgin, E. Better lipids to power next generation of mRNA vaccines. Science. 376 (6594), 680-681 (2022).
- Hou, X., Zaks, T., Langer, R., Dong, Y. Lipid nanoparticles for mRNA delivery. Nature Reviews Materials. 6 (12), 1078-1094 (2021).
- Huang, X., et al. The landscape of mRNA nanomedicine. Nature Medicine. 28, 2273-2287 (2022).
- Rampado, R., Peer, D. Design of experiments in the optimization of nanoparticle-based drug delivery systems. Journal of Controlled Release. 358, 398-419 (2023).
- Kauffman, K. J., et al. Optimization of lipid nanoparticle formulations for mRNA delivery in vivo with fractional factorial and definitive screening designs. Nano Letters. 15, 7300-7306 (2015).
- Jones, B., Nachtsheim, C. J. A class of three-level designs for definitive screening in the presence of second-order effects. Journal of Quality Technology. 43, 1-15 (2011).
- Cornell, J. . Experiments with Mixtures: Designs, Models, and the Analysis of Mixture Data. Wiley Series in Probability and Statistics. , (2002).
- Jones, B. Proper and improper use of definitive screening designs (DSDs). JMP user Community. , (2016).
- Myers, R., Montgomery, D., Anderson-Cook, C. . Response Surface Methodology. , (2016).
- Lekivetz, R., Jones, B. Fast flexible space-filling designs for nonrectangular regions. Quality and Reliability Engineering International. 31, 829-837 (2015).
- Czitrom, V. One-factor-at-a-time versus designed experiments. The American Statistician. 53, 126-131 (1999).
- Karl, A., Wisnowski, J., Rushing, H. JMP Pro 17 remedies for practical struggles with mixture experiments. JMP Discovery Conference. , (2022).
- Lemkus, T., Gotwalt, C., Ramsey, P., Weese, M. L. Self-validated ensemble models for design of experiments. Chemometrics and Intelligent Laboratory Systems. 219, 104439 (2021).
- Gotwalt, C., Ramsey, P. Model validation strategies for designed experiments using bootstrapping techniques with applications to biopharmaceuticals. JMP Discovery Conference. , (2018).
- Xu, L., Gotwalt, C., Hong, Y., King, C. B., Meeker, W. Q. Applications of the fractional-random-weight bootstrap. The American Statistician. 74 (4), 345-358 (2020).
- Ramsey, P., Levin, W., Lemkus, T., Gotwalt, C. SVEM: A paradigm shift in design and analysis of experiments. JMP Discovery Conference Europe. , (2021).
- Ramsey, P., Gaudard, M., Levin, W. Accelerating innovation with space filling mixture designs, neural networks and SVEM. JMP Discovery Conference. , (2021).
- Lemkus, T. Self-Validated Ensemble modelling. Doctoral Dissertations. 2707. , (2022).
- Juran, J. M. . Juran on Quality by Design: The New Steps for Planning Quality into Goods and Services. , (1992).
- Yu, L. X., et al. Understanding pharmaceutical quality by design. The AAPS Journal. 16, 771 (2014).
- Simpson, J. R., Listak, C. M., Hutto, G. T. Guidelines for planning and evidence for assessing a well-designed experiment. Quality Engineering. 25, 333-355 (2013).
- Daniel, S., Kis, Z., Kontoravdi, C., Shah, N. Quality by design for enabling RNA platform production processes. Trends in Biotechnology. 40 (10), 1213-1228 (2022).
- Scheffé, H. Experiments with mixtures. Journal of the Royal Statistical Society Series B. 20, 344-360 (1958).
- Brown, L., Donev, A. N., Bissett, A. C. General blending models for data from mixture experiments. Technometrics. 57, 449-456 (2015).
- Herrera, M., Kim, J., Eygeris, Y., Jozic, A., Sahay, G. Illuminating endosomal escape of polymorphic lipid nanoparticles that boost mRNA delivery. Biomaterials Science. 9 (12), 4289-4300 (2021).
- Lemkus, T., Ramsey, P., Gotwalt, C., Weese, M. Self-validated ensemble models for design of experiments. ArXiv. , 2103.09303 (2021).
- Goos, P., Jones, B. . Optimal Design of Experiments: A Case Study Approach. , (2011).
- Rushing, H. DOE Gumbo: How hybrid and augmenting designs can lead to more effective design choices. JMP Discovery Conference. , (2020).
Reprints and Permissions
Request permission to reuse the text or figures of this JoVE article
Request PermissionThis article has been published
Video Coming Soon
Copyright © 2025 MyJoVE Corporation. All rights reserved