이상적인 가스 법
Overview
출처: 안드레아스 취리히 박사 연구소 - 스위스 재료 과학 및 기술 연구소
이상적인 가스 법은 거의 주변 조건에서 가장 일반적인 가스의 행동과 희석 한계에 있는 모든 화학 물질의 경향을 설명합니다. 측정 가능한 거시적 시스템 변수(압력, 온도 및 부피)와 시스템의 가스 분자 수 사이의 근본적인 관계이며, 따라서 현미경과 거시적 우주 사이의 필수적인 연결고리이다.
이상적인 가스 법의 역사는 압력과 공기의 볼륨 사이의 관계가 반비례로 발견 된 17세기 중반에 날짜, 로버트 보일에 의해 확인 표현과 우리는 지금 보일의 법칙으로 참조(방정식 1).
P  V-1 (방정식 1)
V-1 (방정식 1)
1780년대 자크 찰스의 미공개 작품은 조셉 루이스 게이-루삭에 의해 수많은 가스와 증기로 확장되어 1802년에 보고되어 절대 온도와 가스 의 부피 사이의 직접적인 비례 관계를 확립했다. 이 관계는 찰스의 법칙(방정식2)이라고합니다.
V  T (방정식 2)
T (방정식 2)
기요메 아몬톤은 일반적으로18세기가 되면 고정된 부피 내에서 공기의 온도와 압력 사이의 관계를 처음 발견한 것으로 알려져 있습니다. 이 법은 또한 19세기 초에 조셉 루이 게이 - Lussac에 의해 수많은 다른 가스로 확장되었다 따라서 중 하나 아몬톤의 법 또는 게이 - Lussac의 법으로 언급된다, 방정식에 표시된 바와 같이 3.
P  T (방정식 3)
T (방정식 3)
이 세 가지 관계는 함께 결합되어 수학식 4에서관계를 제공할 수 있습니다.
V  T (방정식 4)
T (방정식 4)
마지막으로, 1811년에, Amedeo Avogadro에 의해 제안되었습니다, 어떤 2개의 가스, 동일 부피와 동일한 온도 및 압력에, 분자의 동일한 수를 포함하는 제안되었습니다. 이것은 모든 가스가 가스의 본질과 무관한 일반적인 상수, 이상적인 가스 상수 R에 의해 기술될 수 있다는 결론을 내렸습니다. 이것은 이상적인 가스 법(방정식 5)로알려져 있습니다. 1,2
PV  T (방정식 5)
T (방정식 5)
Principles
이상적인 가스 법칙, 따라서 그 특성 상수 R, 또한 설득력 분자가 고유 볼륨을 가지고 상호 작용하지 않는 것입니다, 여러 가지 방법으로 첫 번째 원칙 이론에서 파생 될 수있다. 이러한 가정은 희석 물질 한계에서 유효하며, 각분자(예: 주변 조건에서 ~10-23 L)가 점유하는 빈 공간의 부피가 분자 자체(~10-26L)보다 훨씬 크며 상호 작용이 불가능한 경우. 따라서 실온에서 공통 실험실 장비를 사용하는 여러 가지 방법으로 쉽게 입증할 수 있으며, 최대 10bar(도1)까지압력에서 다양한 가스를 사용하여 정확하게 측정할 수 있다. 그러나 이상적인 가스 법은 거의 주변조건(예:프로판)이나 분자 간 상호 작용의 결과로 발생하는 응축, 현상에 대해 밀도가 높은 가스의 특성을 정확하게 설명할 수 없습니다. 이러한 이유로, 국가의 수많은 더 상세한 방정식은 일반적으로 희석 물질 제한에 이상적인 가스 법으로 감소, 발견 이후 몇 년 동안 이상적인 가스 법을 성공했다. 1,2

그림 1. 이상적인 가스법 밀도를 25°C및 0-100 bar 사이의 다양한 다른 일반적인 가스에 비교합니다.
이 자습서에서는 알려진 부피의 일시 중단된 고체 샘플인 정밀 가공 알루미늄 블록을 계량하여 고정 된 부피 내에서 수소 가스의 밀도를 신중하게 측정합니다. 시료의 무게 변화는 아르키메데스의 원칙에 의해 부동되는 유체 밀도의 변화와 직접적으로 관련이 있습니다. 또한 고압에서 보다 이상적인 가스(예: 이산화탄소)를 사용하는 단점도 입증할 것입니다. 마지막으로 수소저장재에 의한 수소방출로 인한 시스템의 부피 의 변동이 측정되는 간단한 벤치탑 실험을 수행하여 이상적인 가스법을 시각적으로 입증하고 질적으로 확인할 것입니다. 이러한 실험 중 하나를 사용하여, 우리는 압력, 온도 및 가스의 주어진 양사이의 관계를 설명하는 범용 상수를 결정할 수 있습니다 - 이상적인 가스 상수, R.
Procedure
1. 샘플의 부피 측정
- 샘플을 주의 깊게 청소하고 건조시다.
- 고해상도 졸업 실린더를 샘플을 덮을 수 있을 만큼 충분한 증류수를 채웁니다. 초기 볼륨 에 유의
- 샘플을 물에 떨어뜨리고 볼륨 변화에 유의하십시오. 이것은 샘플, V의 부피입니다.
- 샘플을 제거하고 건조. 참고: 또는 샘플의 측면 길이를 측정하고 형상을 사용하여 볼륨을 계산합니다.
2. 저울에 샘플을 로드합니다.
- 마그네틱 서스펜션 밸런스에 샘플을 걸어 놓습니다.
- 샘플 주위에 압력/온도 챔버를 설치합니다.
- 시료 환경을 대피시키고 수소 가스로 리필하여 1bar로 리필합니다.
- 샘플 중량을 1bar 및 실온에서측정합니다.
3. 실온에서 압력의 함수로 샘플 무게를 측정
- 샘플 환경에서 Pi0으로압력을 증가하거나 감소시다.
- 샘플 환경이 평형화되도록 합니다.
- 샘플의 무게를 측정, wi0.
- 3.1-3.3을 여러 번 반복합니다.
4. 다양한 온도에서 압력의 함수로 샘플 무게를 측정
- 온도를 Tj로 설정하고 평형할 수 있도록 합니다.
- 수소 가스의 압력을 1bar로 설정합니다.
- 샘플 중량을 1bar 및 Tj,w0j에서 측정합니다.
- Pij로 압력을 증가 또는 감소시키고 평형화할 수 있도록 합니다.
- 샘플의 무게를 측정, wij.
- 4.4-4.5를 여러 번 반복하십시오.
- 원하는 대로 4.1-4.6을 반복하십시오.
5. 이상적인 가스 상수 계산
- P0j가 항상 1 bar이고T 0이 측정된 실온인 경우 측정값 {Tj,Pij및 wij}를표로 합니다.
- 방정식 6 및 방정식 7을사용하여 각 온도 Tj에서 Δwij 및 ΔPij의 차이를 계산하고 표로 합니다.
Δwij = wij - w0j (방정식 6)
Δwij = P ij - P0j = Pij - 1 막대(방정식 7) - 각 측정에 대한 Rij를 계산하고, 모든 값에 대한 평균을 결정하기 위해 이상적인 가스 상수를 결정하고, R. 대안적으로, ΔP ij 및 V의 생성물을 Δwij의 생성물의 함수로서 플롯(분자량, MW로 나눈) 및 Tj,경사, R.(수학 8 및 9)수소, MW=2.01g의 경우 선형 회귀 분석을 수행한다.
ΔP V = Δ nRT (방정식 8)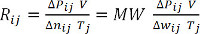 (방정식9)
(방정식9)
Results
이상적인 가스 법은 주변조건(도 1 inset)에 가까운 조건에서 수많은 일반 가스의 실제 가스 특성에 대한 유효한 설명이므로 많은 응용 분야의 맥락에서 유용합니다. 고압 또는 저온 조건에서 시스템을 설명하는 이상적인 가스 법의 한계는 분자 상호 작용및/또는 시스템의 특성에 기여하는 가스 분자의 유한한 크기의 중요성이 증가함에 따라 설명될 수 있습니다. 따라서 강력하고 매력적인 분자 간 상호 작용(수소 결합, 이온-이온-이폴 상호 작용 또는 반 데르 발스 상호 작용을 포함한 다극간 상호 작용에서 발생하는)은 이상적인 가스보다 밀도가 높습니다. 모든 가스는 또한 하나 이상의 분자가 동일한 위치를 차지할 수 없기 때문에 높은 밀도에서 반발 성분을 가지며 이상적인 가스보다 밀도가 감소합니다. 수소와 헬륨 과 같은 가스는 유한한 분자 크기로 인한 반발력에서 더 중요한 기여를 나타내므로 고압에서 밀도가 약간 낮습니다. 메탄과 이산화탄소는 매력적인 상호 작용에서 자신의 특성에 훨씬 더 중요한 기여를 보여줍니다, 그들에게 매우 높은 압력까지 이상적인 가스보다 더 높은 밀도를 빌려, 여기서 반발 용어가 지배 (25 °C에서 100 바보다 훨씬 높은).

그림 2. 평형 흡착 흡수는 25°C에서 높은 표면적, 초활성화 탄화 MSC-30에CO2의 더네m이다.
Application and Summary
이상적인 가스 법은 화학 과학의 이러한 기본 방정식으로, 적어도 첫 번째 근사치에 이르기까지 일상적인 실험실 활동뿐만 아니라 매우 복잡한 시스템의 계산 및 모델링에서 과다한 용도를 가지고 있습니다. 그 적용성은 법 자체에 내재된 근사치에 의해서만 제한됩니다. 이상적인 가스 법이 많은 일반적인 가스에 대해 잘 유효한 거의 주변 압력과 온도에서, 그것은 널리 가스 기반 시스템 및 프로세스의 해석에 사용된다. 이상적인 가스 법을 사용하여 조정할 수 있는 원칙을 사용하는 장치의 두 가지 예는 가스 온도계와 스털링 엔진입니다.
한 가지 특정 응용 분야는 고체 물질의 표면에 가스 흡착 (물리 흡수)의 양을 측정하는 것입니다. 흡착은 가스 분자가 가스 상을 떠나 고체와 가스 사이의 매력적인 분자 간 상호 작용(분산력)으로 인해 고체(또는 액체)의 표면 근처의 밀도상으로 들어가는 물리적 현상이다. 흡착의 역할은 주변 조건에서 많은 벌크 재료 (예 : 유리 및 스테인레스)의 강철을 무시할 수 있지만, 특히 낮은 온도에서 접근 가능한 표면적이 큰 다공성 재료에 매우 중요합니다. 3 체베르트의 방법과 물리적 흡착을 정량화하는 중력 방법은 시스템에서 가스 의 상태의 방정식을 아는 데 의존한다. 저압 및 주변 온도에서 이상적인 가스 법은 많은 가스에 유효하며, 위의 R을 결정하기 위한 프로토콜에 설명된 것과 유사한 방식으로 가스의 흡착량을 정확하게 결정하는 데 사용할 수 있다. 예를 들어, 이상적인 가스 법이 실제로 유효한 조건하에서 고표면적 흡착물의 부력의 중력 측정에서,Δw실제 측정과 Δw이상적 상태의 이상적인 방정식을 사용하여 계산된 Δw 의 차이는 흡착 단계의 중량 변화에 기인할 수 있다. (방정식10) 평형 가스 흡착 이더어는 이렇게 고정 온도에서 압력의 함수로서, Δw광고를이 편차를 표로 하여 측정될 수 있다(그림 2참조), 다공성 물질의 특성화에 대한 표준 절차.
Δw광고 = Δw실제 - Δw이상적 (방정식 10)
References
- Zumdahl, S.S., Chemical Principles. Houghton Mifflin, New York, NY. (2002).
- Kotz, J., Treichel, P., Townsend, J. Chemistry and Chemical Reactivity. 8th ed. Brooks/Cole, Belmont, CA (2012).
- Rouquerol, F., Rouquerol, J., Sing, K.S.W., Llewellyn, P., Maurin, G. Adsorption by Powders and Porous Solids: Principles, Methodology and Applications.Academic Press, San Diego, CA. (2014).
Tags
건너뛰기...
이 컬렉션의 비디오:

Now Playing
이상적인 가스 법
General Chemistry
79.2K Views

일반적인 실험실 유리 제품 및 사용
General Chemistry
658.8K Views

솔루션 및 농도
General Chemistry
275.3K Views

고체 및 액체밀도 결정
General Chemistry
556.8K Views

수성 솔루션에서 질량 백분율 구성 결정
General Chemistry
383.8K Views

경험적 공식 결정
General Chemistry
183.7K Views

이온 화합물의 용해도 규칙 결정
General Chemistry
141.6K Views

pH 미터 사용
General Chemistry
346.9K Views

적정 소개
General Chemistry
425.6K Views

평형 상수의 분광측정 결정
General Chemistry
158.8K Views

르 샤텔리에의 원리
General Chemistry
265.8K Views

알 수 없는 화합물을 결정 하는 동결 포인트 우울증
General Chemistry
160.8K Views

금리법 및 대응 순서 결정
General Chemistry
196.3K Views

차동 스캐닝 열량측정을 사용하여 엔탈피의 변화를 측정합니다.
General Chemistry
44.8K Views

조정 화학 단지
General Chemistry
91.7K Views
Copyright © 2025 MyJoVE Corporation. 판권 소유