结构动力学

通常的重力 (自重) 荷载在结构上有一个根本的区别, 它是准静态的 (即, 它们变化非常缓慢, 或不在所有时间), 和那些由飓风, 爆炸和地震产生, 这是极其动态的性质。在飓风和其他风荷载的情况下, 由于风的频率与典型结构的基本固有频率相比很长, 因此可以将它们的影响建模为实验室的等效静压。这其中的重要例外包括灵活的结构, 如大跨度斜拉桥和悬索桥, 高大的桅杆, 和风力涡轮机结构, 其固有频率的结构可以匹配的风阵风或直风。在地震的情况下, 当地面移动时, 荷载主要是惯性, 而结构往往静止不动。在这种情况下, 载荷取决于结构的实际质量、刚度和阻尼, 而兴趣的数量是结构周围的加速度、速度和位移。如果没有震动表, 这第二组数量很难在实验室中准确地重现。

使用基本物理, 像牛顿的第二定律, 你可以简化结构平衡的问题 (如桥或刚性梁框架), 这是受地面运动 (u_g), 对一个单一自由度质量 (m) 与刚度 (k) 和阻尼 (c) 特性。后两个可以用一个弹簧来表示, 它的力与位移 (u) 成正比, 以及缓冲器的力与速度成正比 (v) (图 1)。这些组件可以并行和/或系列组合, 以模型不同的结构配置。

刚度被定义为按单位量变形结构所需的力。假设一个用已知的力 (P) 加载悬臂梁, 并测量其在尖端 (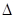) 的弹性变形。刚度被定义为k = P/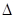.对于简单的弹性悬臂系统, k = L³/3EI, 其中 L 是悬臂的长度, 我是它的惯性力矩, E 是杨氏模量的材料使用。接下来, 想象一下, 如果一个人突然消除了力, 从而允许悬臂振动。一个直觉的人会期望振动的振幅随着每个周期的变化而开始减小。这种现象称为阻尼, 是指一系列复杂的内部机制, 如摩擦力, 往往会减少振荡。阻尼的量化是在本实验室稍后描述的, 但重要的是要注意到, 在这一点上, 不知道这些机制从理论上或实际的立场。一个有用的概念是可视化临界阻尼系数 (c_cr), 它对应的情况下, 悬臂将来休息后, 只是一个完整的振荡。

图 1: 单自由度系统模型。

写出图1所示的系统力的水平平衡方程导致:

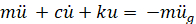(Eq 1)

如果我们看一个简单的例子, 我们可以忽略阻尼, 因为它的影响是微不足道的, 没有外部强迫函数, 等式1成为线性齐次二阶微分方程:

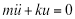(Eq 2)

其解决方案为:

(Eq 3)

区分两次会给我们:

(Eq 4)

将等式4替换为等式 2, 收益率:

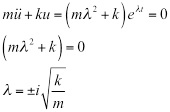(Eq 5)

一般的解决方案是:

(Eq 6)

系统的无阻尼吸自然频率在哪里。

如果这个系统被给一个最初的位移() 和/或者初始速度 (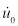), 等式6成为:

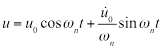(Eq 7)

如果我们增加阻尼 (c) 和定义的效果, 系统的阻尼固有频率就会变成 , 等价于等式 7:

(Eq 8)

对于初始位移 u₀的情况, 图2显示了几个值的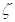行为。

图 2: 阻尼对自由振动的影响: 临界阻尼的定义 (上部);从对数递减 (下) 计算阻尼。

如果在图2中, 你定义, u_n 和u_{n +}1是连续周期的位移, 然后:

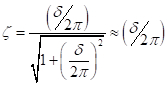(Eq 9)

回到等式 1, 如果地面运动被采取正弦作用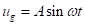 , 等式8的类比是:

(Eq 10)

相位滞后在哪里, R_a 是放大响应因子, 图3中说明了其图形。图3显示, 对于低值的阻尼 (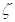 < 0.2), 由于强迫函数的频率接近系统的固有频率, 系统的响应变得不稳定, 这种现象通常称为共振。

图 3: 位移、速度和加速度响应。

在这个实验中, 我们将用一个震动表在结构动力学的背景下, 实验性地研究概念并推导出方程 1-10 的背后。

首先, 确定每个模型发生最大位移的频率 (ω)。最初讨论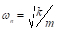的简单公式, 需要修改, 因为光束本身的质量 (m_b = w_光束/g), 分布在其高度, 是不可忽略的与质量在顶部 (m = w_块/克)。等效质量为悬臂梁的情况是 (m + 0.23m_b), m是质量在顶部和m_b 是束的分布的质量。刚度k由单位力在悬臂顶部引起的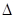变形 () 的倒数给出:

(Eq 11)

我是光束的长度, E是弹性的弹性模量, 而我是惯性的时刻。给我的是 , b是宽度, h是光束的厚度。因此, 悬臂梁的固有圆频率, 包括自重是:

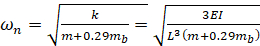(Eq 12)

基于这个方程, 预测的自然频率计算在表1。

光束数	长度 在	宽度 (in.)	厚。 (in.)	我 (4)	电子邮件 (ksi)	重量 磅	光束重量 (磅)	有效质量 (磅 2/秒)	自然频率 (每秒转数)
1	12。0	1.002	0.124	1.59E-04	10200	0.147	0.149	4.70E-04	2.45
2	16。0	1.003	0.124	1.59E-04	10200	0.146	0.199	4.97E-04	1.55
3	20。0	1.002	0.125	1.63E-04	10200	0.146	0.251	5.28E-04	1.09
4	24。0	1.003	0.125	1.63E-04	10200	0.148	0.301	5.63E-04	0.80
5	28。0	1.001	0.125	1.63E-04	10200	0.144	0.350	5.82E-04	0.62
6	32。0	1.000	0.124	1.59E-04	10200	0.146	0.397	6.15E-04	0.49
7	36。0	1.002	0.126	1.67E-04	10200	0.147	0.455	6.52E-04	0.41
8	40.00	1.000	0.125	1.63E-04	10200	0.148	0.500	6.81E-04	0.34

表 1: 试验了悬臂梁的固有频率。

在表2中比较了模型系统正常频率的测量和理论值。通过仔细地将悬臂梁置换1英寸, 然后观察位移与时间响应, 计算出实际的固有频率。下面的比较是以句点 (t_d,秒) 的方式进行的, 因为这些是从 t_d = u₀-u₁确定的, 如图 2(b) 所示。这需要谨慎和耐心才能取得可靠的结果。显示的演示只是为了给出系统行为的总体说明。

光束数	自然频率 (每秒转数)	预测周期 秒	实际期间 秒	错误 (%)
1	2.45	2.56	2.65	-3.33%
2	1.55	4.06	4.23	-4.22%
3	1.09	5.78	6.79	-17.52%
4	0.80	7.84	8.04	-2.54%
5	0.62	10.06	10.63	-5.70%
6	0.49	12.79	13.04	-1.97%
7	0.41	15.32	16.78	-9.50%
8	0.34	18.59	20.56	-10.59%

表2。结果的比较。

不同之处主要是由于横梁不刚性附着在木制底座上, 加上底座的弹性增加了结构的周期。另一个错误的来源是, 在计算中没有考虑到阻尼, 因为阻尼很难测量和振幅依赖性。

接下来, 从每个位移与时间历史, 提取每个频率的最大值, 并绘制位移与规范化频率的大小, 如图 3所示。如图 4所示, 我们有归一化频率与第一自然频率 (光束数 1), 并绘制了该光束的最大位移, 当震动台受不同的正弦变形时, 振幅为1 in。

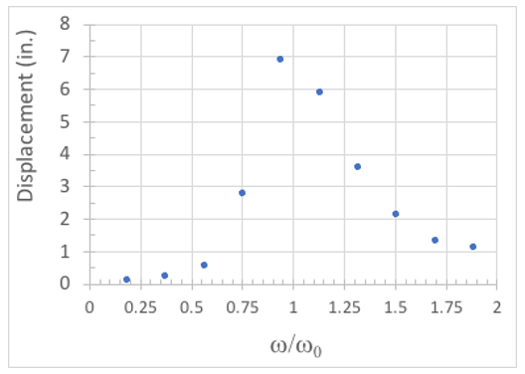
图 4: 梁的变形 #1 与规范化的工作台频率有关。

最初, 当ω/ω_n的比值较小时, 由于表运动的能量输入并不能激发模型, 所以没有多少响应。当ω/ω_n接近1时, 响应会有很大的增加, 变形变得相当大。当ω/ω_n非常接近1时, 最大响应达到。随着归一化频率的增加超过ω/ω_n = 1, 动态响应开始下降;当ω/ω_n变大时, 我们处于一种情况, 即负载在结构的固有频率上非常缓慢地应用, 变形应与静态施加的负载相等。

这些实验的目的主要是显示行为的变化定性, 如示范为两个框架结构。获得类似图3和4所示的结果需要极大的谨慎和耐心, 因为摩擦力和类似的来源会影响阻尼量, 从而将类似于图 3(c) 中的曲线转换为实际阻尼频率, 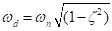变化。

在实验中, 采用摇臂法测量了简单悬挑系统的固有频率和阻尼。尽管地震的频率内容是随机的, 并且覆盖了大量的频率, 但通过傅里叶变换将加速度时间历史转化为频域, 可以发展频谱频谱。如果地面运动的主要频率与结构相匹配, 那么结构很可能会发生较大的位移, 从而受到巨大的破坏甚至坍塌。地震设计着眼于根据历史记录, 地震源的距离, 地震源的类型和大小, 以及地表和体波的衰减来确定一个给定位置的地震的加速度水平合理的加速度水平用于设计。

公众通常不知道的是, 目前的抗震设计规定只是为了尽量减少崩溃和生命损失的可能性, 在这种情况下, 最高可信的地震发生在一个可接受的水平 (在大多数情况下约5% 至10%例)。虽然结构设计, 以获得较低的可能性的失败是可能的, 他们开始变得不合算。在今天没有明确考虑这类事件之后, 减少损失和提高复原力, 尽管这种考虑越来越普遍, 但在许多时候, 建筑物的内容及其功能可能比其安全性要重要得多。例如, 一个核电厂 (如2011大关东地震中的福岛), 洛杉矶的住宅十层楼, 或硅谷的电脑芯片制造设施, 以及它们暴露和易受地震影响的案例。事件。

就核电厂而言, 最好是设计结构, 以尽量减少任何损坏, 因为即使是极小的失败的后果也会产生非常可怕的后果。在这种情况下, 我们应该设法尽可能远离地震源找到这个设施, 以尽量减少暴露, 因为尽量减少对所需水平的脆弱性是非常困难和昂贵的。现实是, 这是非常昂贵的这样做, 因为公众的愿望不仅要避免福岛类型的事件, 而且甚至更有限的, 像三英里岛上的核灾难。

对于洛杉矶的多层建筑来说, 要最大限度地减少暴露的风险是很困难的, 因为在附近有一些未知的返回周期的地震断层网络, 包括圣安德烈的断层。在这种情况下, 重点应是稳健的设计和详细说明, 以尽量减少结构的脆弱性;住宅的业主应该意识到, 如果发生地震, 他们将承担重大风险。他们不应该期望大楼倒塌, 但如果地震规模足够大, 这座建筑物可能会完全失去。

对于计算机芯片厂来说, 问题可能是完全不同的, 因为结构本身可能是相当灵活的, 外部的频率范围的地震。因此, 该结构可能不会受到任何损害;然而, 它的内容 (芯片制造设备) 可能会受到严重损坏, 芯片生产可能会中断。根据工厂生产的特定芯片集, 对工厂的所有者和整个行业的经济损害都是巨大的。

这三个例子说明了为什么需要为我们的基础架构开发弹性设计策略。为了达到这个目标, 我们需要了解输入 (地面运动) 和输出 (结构响应)。这个问题只能通过一个综合的分析和实验方法来解决。前者反映在上面列出的等式中, 而后者只能通过准静态、伪动态和震动表方法完成的实验工作来实现。